基于冲积系统趋衡响应模型的河床冲刷研究与预测

景 唤，张红武，王彦君，王永强，钟德钰

(1.长江水利委员会长江科学院 水资源与生态环境湖北省重点实验室，湖北 武汉 430010；2.长江水利委员会长江经济带保护与发展战略研究中心，湖北 武汉 430014；3.清华大学 水沙科学与水利水电工程国家重点实验室，北京 100084)

1 研究背景

上游来水来沙条件、河床边界条件及下游侵蚀基准面是影响冲积河流河床演变的主要因素[1-2]。在河流上修建水库之后，工程的拦沙调蓄作用使进入下游河道的水沙过程发生显著变化，河流因得不到足够的泥沙补充而发生长距离持续冲刷，自上而下造成干流河道河床高程及特征水位显著下降，甚至会在支流中诱发自下而上的溯源冲刷，改变河道的防洪减灾局面。

关于冲积河流尤其是水利枢纽下游河道的沿程冲刷发展特性，以往学者开展了大量研究。例如，程晓陶等[3]以二维非恒定流与不平衡输沙理论为基础，探索了洪水演进过程中黄河下游花园口-孙口河段的滩槽冲淤特性；张红武等[4]通过模型试验开展了小浪底水库拦沙期下游游荡性河段的演变趋势研究，并运用一维水沙数值模型对小浪底水库运用初期其下游河道的冲淤过程进行了预测，发现工程设计水沙系列下黄河下游河道将产生自上而下的冲刷，冲刷量沿程呈显著衰减趋势[5]。陈建国等[6-7]基于实测资料对小浪底水库拦沙运用后黄河下游河道沿程冲刷下河槽形态的调整趋势展开了深入探讨。安催花等[8]运用实测资料分析、水沙数值模拟等方法，给出了黄河下游河道未来来水情势及现有工程联合调控下的平衡输沙阈值，为下游河道的减淤治理提供了依据。

至于溯源演化的空间分布特性研究，陈建国等[9]基于实测资料对三门峡水库不同运用方式下库区的溯源冲刷过程进行了研究。张俊华等[10]基于物理模型试验分析了小浪底水库运行初期异重流排沙下干流高含沙水流倒灌在支流内引起的溯源淤积及库水位大幅下降在库区干流和支流引起的溯源冲刷发展特性。此外，王兆印[11]、李昌志等[12]在研究潼关高程变化下渭河下游河道的河床演变特性时指出，潼关高程抬升和下降引起的溯源淤积和溯源冲刷以冲淤行波的形式向上游传播，且溯源冲淤幅度自下而上逐步减弱。随后，卜海磊等[13]假设溯源冲刷前后河道纵剖面均为直线，建立了冲淤平衡时河床比降与水沙特征值的定量关系，据此对小浪底水库拦沙期其下游河床冲刷引起的沁河下游河道的溯源冲刷深度进行了预测。本文基于河流辩证法及河流动力学原理，在实测资料检验率定的基础上，对所建立的冲积系统趋衡响应模型初步形式进行提升研究，提出一种新的非平衡态冲积河流时空调整过程的描述方法，据此对黄河中游古贤水库修建后下游河道的冲刷状况进行预测，并对潼关高程降低引起的渭河下游的溯源冲刷问题开展研究。

2 趋衡响应模型方法

2.1 冲积系统的趋衡响应模型现代河流辩证法表明[1]，冲积河流作为开放系统，在流域水沙运动与演变影响下通常处于非平衡状态，尽管在一定时期内河流系统可能处于相对稳定或平衡的状态，但河床绝对和静止的平衡是不存在的，尤其在受到以水沙、边界改变为代表的外部扰动后，冲积系统必然偏离原有的相对平衡状态，且在趋于新平衡态的过程中，水流与河床的相互作用总是使偏差朝减小的方向调整。为此，本文将流域水沙、边界条件变化下，非平衡态冲积系统通过河道形态的不断调整，对外部扰动的响应强度随时间推移而不断衰减，最终消除外部扰动影响而趋向于新平衡态的过程称之为“趋衡响应过程”，而将这一朝新平衡方向发展的河流趋向或基本特性，归结为冲积河流演变的时空“趋衡性”[14]或“趋衡响应原理”[15]。假定外部扰动的发生概率符合泊松分布，且单个扰动引发的系统响应强度随时间满足指数衰减律，运用统计力学中的随机理论，不难推导得到扰动后非平衡态冲积河流趋衡响应过程的控制方程如下[14]：

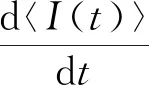
(1)

式中：〈I(t)〉为非平衡态冲积河流的河道形态特征变量(指河床形态调整强度)；〈Ie〉为河道形态特征变量演化的平衡值；α为衰减系数。

(2)

该式即为非平衡态冲积河流的河床演变波方程，可用于描述突发扰动后非平衡态冲积河流河床演变波的时空动态演进与衰减过程。此时，若考虑河道形态特征变量接近平衡(即t→∞)，则偏微分方程中时间变化项接近于零，因此将其从式(2)中去除，控制方程可简化为

(3)

式中〈I(xe)〉为外部扰动后接近平衡状态的河道形态特征变量在x→∞处的取值。该式即为描述扰动后河流形态接近平衡时研究河段内河道形态调整强度空间分布状况的微分方程，求解即为河流非平衡态空间响应过程的理论公式

〈I(x)〉=(1-e-αx/ν)〈I(xe)〉+e-αx/ν〈I(x0)〉

(4)

式中：〈I(x)〉为任意位置x处的河道形态特征变量随时间演化的平衡值；〈I(x0)〉为初始位置河道特征变量随时间演化的平衡值；v为河床演变波传播速率；x/v有与时间类似的概念；α/v为趋衡衰减系数，可体现河床形态调整强度的沿程衰减速率。

将上式整理变换可得：

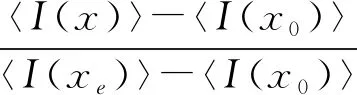
(5)

式中左侧(〈I(x)〉-〈I(x0)〉)/(〈I(xe)〉-〈I(x0)〉)为一无量纲参数，表征冲积河流特征参数的空间调整完成度，其取值范围是[0，1]。在计算起点其值为0，在不受扰动影响的平衡区域时，即空间位置x→∞时，其值为1，表明外部扰动的影响已完全衰减消失。无量纲参数增大的过程即外部扰动诱发的冲积系统的内部响应随着距扰动点距离的增长逐渐消失的过程。不难看出，趋衡衰减系数α/v是本冲积系统趋衡响应模型的关键参数，决定了扰动后河流系统特征变量时空调整的趋衡响应定量规律，从而使该趋衡响应模型能够描述冲积系统特征变量的时空调整发展过程。

需要说明的是趋衡响应特性不仅是冲积系统的重要属性，而且普遍存在于生态环境、人文地理等领域的多尺度物理过程中，甚至传播学中诸如新闻热度、特征重要度等指标的衰减速度亦和当前值与平衡值之差成正比并随时间呈指数衰减趋势。尽管研究学科不同，但因系统趋衡响应特性遵循相同的时空衰减规律，故建立的方程形式也可能完全一致。例如上述冲积河流趋衡响应方程和微观电子脉冲电流方程具有相似的形式。文献[16]就水利工程对生态系统的胁迫作用问题开展了研究，将水利工程通过形成新的平衡和利用自身优势对生态系统产生的有利作用称为“逆胁迫作用”，认为水利工作者即可在规划设计与科学论证阶段，通过水工程生态调度实现物种及其生境保护和环境影响消减，利用系统趋衡响应原理，充分发挥水利工程的“逆胁迫作用”。

2.2 典型工程应用示例及深化研究

2.2.1 美国多个水库下游河道的沿程冲刷示例 选取美国多条典型冲积河流上枢纽下游河道河床冲刷深度实测数据[17]对冲积系统趋衡响应模型进行应用示例，选取的研究河段涉及的河流和水库名称如表1所示。

表1 研究河段涉及的河流和水库名称

结果如图1所示，横坐标αL/v表示相对历时(其中，L为河流非平衡态演变的平衡距离)，纵坐标(δIx-δIx0)/(δIxe-δIx0)表示水库拦沙运用后其下游河道河流非平衡态演变中河床累计冲刷深度空间调整的完成度，其中δIx为河床累计冲刷深度在距离坝址x处的取值，δIx0和δIxe分别为其初始值与平衡值，考虑到水库蓄水拦沙造成的下游河道来沙量骤减所引起的影响终将完全消失，理论公式中平衡值为0。图中实线为理论曲线。观察可得，冲积河流上水库蓄水拦沙运用后下游河道河床累计冲刷深度先后经过“调整区”(指河流非平衡态演变中河道形态特征变量不断调整的区域)后，逐渐进入“未扰动区”(指水沙变化的影响基本被吸收，河道形态特征变量不再大幅调整的区域)，整个非平衡态空间趋衡响应过程均服从统一的理论曲线。可以看出，冲积河流特征参数的调整完成度变化速率沿程非线性减缓，即靠近枢纽处，河床调整速度较快，远离枢纽处调整速率逐渐减缓，呈现典型的负指数衰减特征。以上结果表明，基于冲积河流的趋衡响应原理所得的理论模型能够很好地预测水库运用后其下游河道的沿程调整过程，体现了河床演变的时空趋衡性。

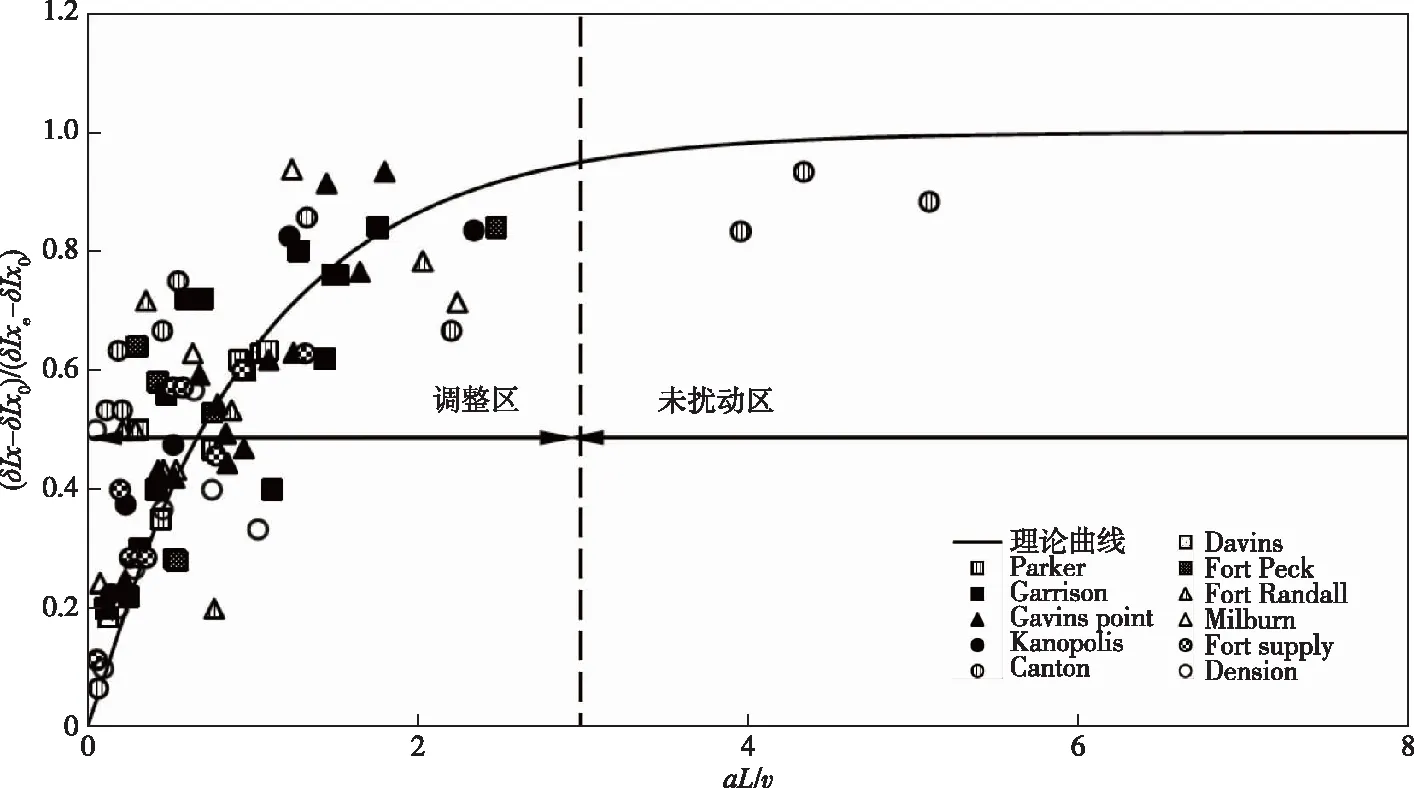
图1 美国若干水库下游河道的沿程调整过程

对于趋衡衰减系数α/v，因所选取的美国各个水库下游冲刷河段河长普遍较短，大多在几公里至几十公里不等，研究河段水沙特性沿程相差不大，在探索水库运用后其下游河道的非平衡态演变规律时，将趋衡衰减系数α/v暂视为常数，其取值情况见表2(因同一河流上修建多个大坝而将河道分隔为若干研究河段，表中以河段进口大坝名称来表征河段)。可以看出，在不同河段间，进入河道的年平均流量相差甚远，在1.90～680 m3/s不等，最大值和最小值相差数百倍，同样地，不同河段间趋衡衰减系数α/v取值也差异显著，在0.012～0.400不等，最大值与最小值间相差数十倍。可见，河道形态的沿程调整特性与水沙特性密切相关。

表2 不同研究河段趋衡衰减系数α/v率定结果

上述结果表明，在水库拦沙运用影响下，枢纽下游河道的沿程调整虽遵循统一规律，但在不同研究河段间，因河道水沙条件及河床物质组成特性的差异，河道形态调整幅度的沿程衰减速率，即趋衡衰减系数α/v取值大相径庭。本文趋衡响应模型中综合衰减系数α/v与河道水沙特性、河床物质组成等相关，利用实测资料加以率定后，才能用来预测受到外界扰动后不同冲积河流特征形态参数变化量在空间上的分布规律，成为基于“趋衡响应原理”的冲积河流特征变量时空调整预测方法。

2.2.2 模型深化研究 为进一步提高本文趋衡响应模型的实用性，需运用水力学及河流动力学原理[18-21]，在充分分析河道来水来沙条件及河床物质组成特性的基础上，建立初步模型关键参数与河道水沙要素的关系[22]，甚至还应考虑沿程挟沙能力的变化[23]。作为初步研究，本文拟选取泥沙起动难度与水流强度作为反映影响床面泥沙运动状态的两个矛盾方面，对上述模型进行深化研究。

水沙变化等外部扰动下，非平衡态冲积河流的床面泥沙运动状态受两方面影响，其一为水流促使床面泥沙运动的力，称之为驱动力，主要由水流强度反映；其二为床面泥沙抵抗水流影响的力，称之为阻尼力，主要由床沙起动难易程度来反映。

通常而言，弗劳德数Fr是表征水动力条件的常见参数[18-21]，反映了特定断面上惯性作用和重力作用的对比关系，与水流流态密切相关，其值越大，意味着水流强度越强，对床面泥沙的驱动越强，床沙被搬运的概率越大，河床愈趋向于冲刷。文献[24]在研究冲积河流糙率时曾发现，Fr能够体现水流的摩阻特性，与糙率n存在显著的相关关系，两者在数量关系上呈反比，受1961年张瑞瑾选用Fr作为描述沙波运动参变量的启发[21]，文献[24]基于由动床模型试验结果按比尺换算成的原型资料，建立了摩阻厚度δ*同Fr及D50的关系，其表达式如下：

(6)

该研究首次在水流阻力研究中突出了Fr的影响，从定量上描述了黄河下游河道当Fr=0.5时沙波消失使δ*最小(床面为动平床)以及Fr>0.5后因逆行沙波逐渐出现使δ*复而增加的规律。随后，张红武等[18]根据国内外糙率表并结合黄河糙率表现，指出冲积河流糙率最大值一般为糙率较小值(约为动平床糙率)的10倍左右，同时发现Fr跟含沙量呈正比，且Fr在很大程度上已体现了水流条件对含沙量的影响，最终建立了糙率n和弗劳德数Fr的简便式：

(7)

该式在黄河、渭河等多条河流资料的验证中取得了良好的效果，说明Fr还能间接反映水流的摩阻特性乃至含沙量的影响，故可以作为表征水流驱动力的水动力学参数。

同样地，描述床面泥沙起动难易程度的参数有临界切应力τc、Shields数、起动流速UC等[19-21]，其中临界切应力τc因测量困难难以广泛应用，而应用较为广泛的Shields曲线因其为双对数坐标，数值的微小差异本身难以反映[25]，且相同横坐标下的点群分散幅度较大，原曲线走向也有一定人为性，尤其当沙粒雷诺数大于200及小于1时，曲线走向与实际点群分布偏离，在应用时可能出现较大偏差[21]，在反映床面泥沙起动难易时有一定局限。在此背景下，鉴于流速场和剪力场间的密切关系，根据河床物质组成及泥沙相对起动特性直接影响河床冲刷调整的角度，可将起动流速UC作为表征床面阻尼力的参量。

综上所述，本文选取弗劳德数Fr和泥沙起动流速UC两个关键参量，反映水流驱动作用及床沙阻尼作用，以起动流速与弗劳德数之比代表影响床面泥沙运动状态的两个矛盾方面，将其作为修正趋衡减系数α/v的河流动力学参量，据此，可得：

(8)

式中：k、b为待定系数，与研究河段有关；UC为泥沙起动流速，可选取更为适应黄河泥沙及摩阻特性的张红武公式[20]计算：

(9)

式中：KD为系数，与涡团参数及谢才系数有关；γ为清水容重；γs为泥沙容重；γ′为河床淤积物的干容重；γ′c为河床淤积物的稳定干容重；υ为水流运动黏滞系数；δ为薄膜水厚度；D为床沙粒径，h为水深；g为重力加速度。

将式(8)代入式(4)，即可得到冲积河流非平衡态空间响应典型过程的计算公式：

(10)

以黄河铁谢为起点(x=0)，清华大学在确定太澳黄河公路特大桥河床冲刷深度时，曾借鉴三门峡水库下泄清水期下游河道实测资料，综合分析得出铁谢河床平均冲刷深度为3.2 m，可确定式(10)中的参数〈I(x0)〉。1990年代初李保如、张红武等在开展南水北调中线穿黄渡槽所在河段河床演变及选线问题研究时[25]，利用三门峡水库下泄清水期裴峪至官庄峪河段(约39 km)累计冲刷量3.8亿t、河槽冲刷宽度3300～4000 m的实测资料，按冲刷宽度上下限分别得到河床平均冲刷深度为2.51 m和3.04 m。因裴峪、官庄峪分别位于伊洛河入黄口上下游一定距离，河槽上窄下宽，故裴峪断面应取冲刷深度为3.04 m，官庄峪断面应取冲刷深度为2.51 m。根据裴峪和官庄峪水动力实测资料，可确定裴峪至官庄峪河段的河流动力学参数UC/Fr，接着将水库下游裴峪、官庄峪的河床冲刷深度实测数据代入式(10)，率定可得到趋衡响应公式系数，结果见表3。从而，构建了水库运用后枢纽下游河道河床累计冲刷深度定量预测的修正方法。

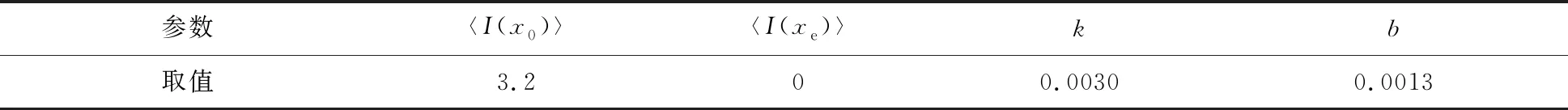
表3 式(10)系数率定结果

2.2.3 三门峡水库拦沙期下游沿程冲刷验证计算 为更好预测系统扰动后冲积河流时空调整规律，需进一步选用三门峡水库拦沙期下游河床平均冲刷深度的实测资料[26-27]对趋衡响应模型进行系统验证，黄河下游河道典型断面的河流动力学参数见表4。

表4 黄河下游河道典型断面的河流动力学参数

基于趋衡响应公式的系数率定结果，运用三门峡水库拦沙期下游铁谢至利津河段1960—1964年特征水位转化得到的断面河床平均冲刷深度的实测资料[27](图中以黑色实心圆形标记显示)，对理论模型进行验证，结果见图2。可以看出，三门峡水库下游河道河床平均冲刷深度沿程呈递减趋势，河床实际平均冲刷深度与曲线整体符合良好。需要说明的是三门峡水库因泥沙淤积问题暴露，使拦沙期下游冲刷未达到充分状态即不得不改变运用方式，出现部分实测点位于曲线以下是符合实际的。笔者认为这组资料中利津站冲刷深度明显偏小，为此本文进一步分析了三门峡水库下泄清水期下游利津站断面资料：由1962年汛前与1964年汛后断面之差得冲刷面积为616 m2[26]，河槽宽度即使按2000 m计，三门峡水库下泄清水时利津的冲刷深度仍然为0.31 m(图中以“×”符号显示)，与计算值接近，并能体现若三门峡水库拦沙运用方式不改变，下游河床还会继续冲刷的实际情况(其后小浪底水库拦沙期泄流强度虽弱于三门峡水库，但由于长期冲刷，下游河床冲刷深度普遍超过三门峡水库下泄清水期对下游的冲刷)。对于水库下游河道冲刷深度呈沿程递减趋势，其特性与泥沙的沿程补给有关，水库拦沙运用使进入下游河道的沙量骤减，河流因物质补充不足而进入冲刷过程，且随着冲刷发展水流逐渐获得补给，河道对于水沙变化的响应强度即冲刷强度逐步减弱，冲刷深度沿程递减而趋向平衡，最终实现空间上的趋衡演变；而对于冲刷深度的沿程衰减速率，其快慢与水库运用造成的水沙变化及河道物质组成关系密切[28]，由于泥沙的分选作用，下游河道床沙沿程细化，泥沙黏性影响凸显，加之河道逐渐趋于窄深，泥沙起动更为困难，冲刷深度的沿程衰减速率也有所增大。此外，注意到理论曲线约在距铁谢1000余km处才可能衰减接近于0，冲刷可一直延伸至河口，即三门峡水库运用可造成黄河全下游河道的冲刷，这一点与真实情况相符[28]。

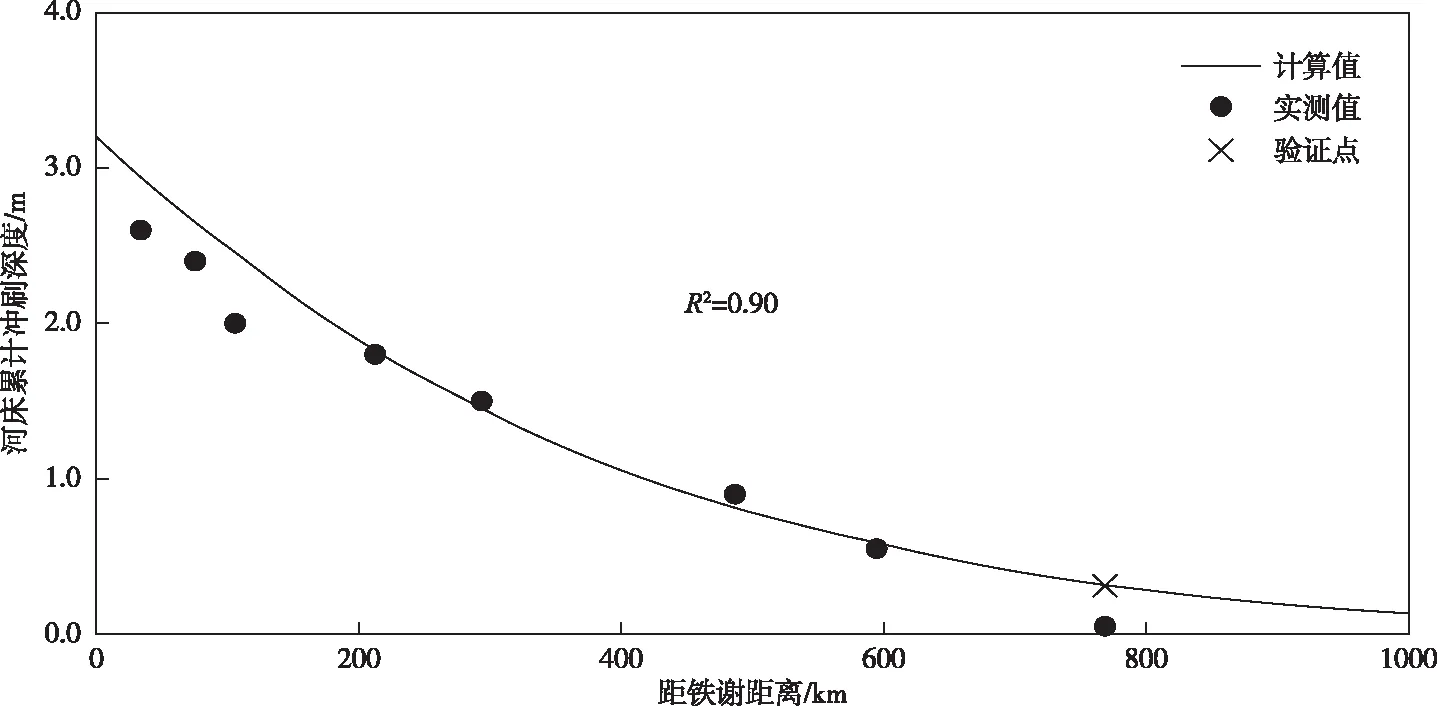
图2 三门峡水库下游沿程冲刷深度分布验证结果

3 黄河中游河道的冲刷预测

当前，黄河水沙调控体系的主体框架尚未形成[29-30]，中游段修建古贤水利枢纽，对黄河治理与国家能源、粮食与生态安全保障意义重大[30]。文献[30]从多方面探讨了古贤水利枢纽对黄河流域保护与发展的战略作用，指出其可有效促进工程下游河道过流能力恢复，同时减轻渭河防洪压力等[30-31]，对于中下游河道防洪减淤等具有重要的工程价值。此外，在入库来沙量大为减少的现状下[32]，三门峡水库运用方式应该优化调整，使这一黄河明珠重放光芒[31]。

本节将运用趋衡响应模型，对古贤水库修建后引起的下游河段的沿程冲刷深度尤其是潼关高程变化进行预测，并对潼关高程下降引起的渭河下游河道的溯源冲刷深度进行模拟计算。

3.1 古贤水库下游沿程冲刷预测考虑到三门峡水库下游的铁谢至桃花峪河段与古贤水库下游的禹门口至潼关河段均位于黄河中游段，两者沿程趋衡响应特性相近，故而将依据三门峡水库下游河床冲刷实测资料率定所得式(10)中的系数k和b的取值作为古贤水库下游河道趋衡响应模型的系数值并进行计算。古贤水库下游河道的河流动力学参数见表5。此外，因古贤水库下游河道和三门峡水库下游河道河床组成、水深、糙率等存在可类比性但又不完全相同，两座水库下游河道的河床冲刷潜力存在一定差别。鉴于对河床冲刷影响最直接的是床沙的起动输移，床沙越难起动，河床最大冲刷深度越小，对于古贤水库下游计算起点(这里以禹门口为计算起点)河床冲刷深度的确定，可以假定起动流速与冲刷深度呈反比，利用三门峡水库下游裴峪断面累计冲刷深度、床沙起动流速和古贤水库下游禹门口断面床沙起动流速资料，推算禹门口河床冲刷深度。亦即，裴峪床沙中值粒径D50约为0.19 mm，水深约为2.5 m，糙率n约为0.0135，以式(9)计算得到起动流速UC=0.21 m/s；禹门口床沙中值粒径D50约为0.42 mm，水深约为3.9 m，糙率n约为0.022，以式(9)计算得到起动流速UC=0.33 m/s，由此根据裴峪冲刷深度为3.04 m(选用上文依据冲淤量反算所得河床冲刷深度)确定禹门口冲刷深度约为1.90 m。据此即可对古贤水库运用后下游代表站点的冲刷深度进行初步预测，结果见表6。

表5 古贤水库下游河道典型断面的河流动力学参数[33-34]

表6 古贤水库下游河道冲刷深度初步预测结果

3.2 渭河下游河道溯源冲刷预测渭河是黄河最大的支流，于潼关注入黄河[35-36]。由于黄河干流在位于黄河和渭河交汇口的潼关处流向急转，河宽骤缩，形成天然卡口，潼关高程对渭河下游段起到了局部侵蚀基准面的作用[37-39]。三门峡水库蓄水运用后，库区泥沙大量淤积使得潼关高程不断抬升。受潼关高程居高不下及渭河不利的来水来沙条件影响，渭河下游段呈严重淤积状态[40-43]。黄河中游古贤水库修建运行后，其下游河道的沿程冲刷将使潼关高程下降，并进而在渭河下游段内引发自下而上的溯源冲刷过程。

(1)溯源冲刷深度预测与特性分析。基于修正的趋衡响应模型式(10)及古贤水库下游河道冲刷预测得到的潼关高程下降值对潼关高程下降在渭河下游段内引起的溯源冲刷过程进行预测。渭河下游段典型断面的河流动力学参数见表7。

表7 渭河下游段典型断面的河流动力学参数

计算时将潼关修正后的河床冲刷深度作为初始条件〈I(x0)〉，考虑到本文计算的渭河下游段的溯源冲刷过程为设想情景，缺乏用于模型系数率定的完全吻合情景的河床冲淤实测资料，因而以潼关高程变化在渭河下游段内引起的典型溯源冲淤过程的实测数据为基础，大致估计其溯源冲淤的时间衰减系数α和传播速率v取值，进而确定系数k和b值。图4(a)为潼关高程变化过程，图4(b)为潼关高程历史上一次典型抬升期后渭河下游段累计淤积量实测数据及相应的分析计算结果，曲线中时间衰减系数α取值为0.090。同时，根据文献[11]不同时期渭河下游段单位河长年均淤积率或冲刷率的分布图中较为完整的一次溯源冲刷过程，冲刷波在渭淤1—渭淤7、渭淤7—渭淤12、渭淤12—渭淤18河段的年均传播速度可取7.5 km/a、5.0 km/a和4.0 km/a。

图4 渭河下游段累计淤积量随时间的变化过程

将以上资料代入式(8)求解得到的k、b依次约为0.015和0.0021，据此即可预测潼关高程下降在渭河下游段内引起的溯源冲刷变化，结果如图5及表8所示。由图可知，潼关高程下降引起的渭河下游段溯源冲刷深度的沿程分布呈现典型的衰减特性，这一点与王兆印、李昌志等[11-12]等在研究潼关高程变化对渭河河床演变影响时得出的结论一致。此外，由图估算得到潼关高程下降1.43 m产生的渭河下游段的溯源冲刷行波能够传播的最长距离(即潼关高程变化引起的渭河下游段溯源冲刷长度)约为250 km，这一结论亦与清华大学的研究结论[44]及文献[45]的模拟结果基本一致，一定程度上证明了预测结果的合理性。

表8 两种方法下溯源冲刷深度计算结果比较

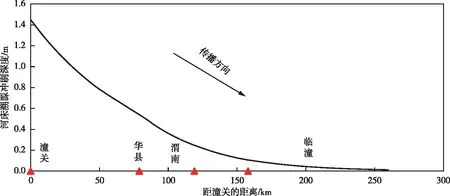
图5 渭河下游段溯源冲刷深度的沿程分布

(2)与卜海磊[13]方法计算结果比较。卜海磊[13]对小浪底水库拦沙期沁河入黄口河床冲刷引起的沁河下游河道的溯源冲刷问题进行了研究。在建立支流溯源冲刷距离和冲刷深度计算公式时，假定初始纵剖面和冲刷后纵剖面均为直线，联立水流连续方程、输沙平衡下的输沙率公式、张有龄糙率公式得到溯源冲刷距离和冲刷深度的微分方程并解得：

(11)

(12)

式中：Z0为河口侵蚀基准面降落深度，m；J0为冲刷前河床纵比降；S0为引起溯源冲刷的来流含沙量，kg/m3；γ0为河床淤积物的干容重，kg/m3；q为造床流量下的河道单宽流量，m2/s。

运用卜海磊方法[13]对潼关河床冲刷下降后，渭河下游段溯源冲刷深度的沿程分布进行预测，取初始河床比降J0为0.15‰，河床淤积物干容重γ0为1500 kg/m3，造床流量为2500 m3/s，河床冲刷宽度初步取相关断面平均值，得出单宽流量q约为5 m2/s。为尽量采用与上文渭河下游段溯源冲刷预测同一时期数据，采用1987—2010年渭河下游段的多年平均悬移质含沙量作为引起溯源冲刷的来流含沙量，含沙量S0为45.8 kg/m3。鉴于渭河主要来沙支流泾河近年来因东庄水库建成生效而减沙作用显著，引起渭河溯源冲刷的来流含沙量减少，保守起见，这里按减沙比例35%计，取来流含沙量S0为30 kg/m3，同时期上述造床流量历时约为21.1 d。此处冲刷历时参照卜海磊[13]计算沁河下游段溯源冲刷的算例，确定渭河下游段溯源冲淤响应历时为4 a，相应造床流量下冲刷历时共计约84.3 d。将上述条件代入式(11)计算得到平衡比降约为0.16‰。按初始纵剖面和冲刷后纵剖面均为直线的假设，可得潼关河床高程下降1.43 m所引起的渭河下游段各站溯源冲刷深度(见表8)。可以看出，本文方法计算所得溯源冲刷深度与卜海磊方法较为接近，但本文方法给出的冲刷剖面相对更符合实际。

4 结论

(1)基于河流辩证法原理，认为处于相对稳定状态的河流受到外部扰动后，必然偏离原有的相对平衡状态，在趋于新平衡态的过程中，水流与河床的相互作用总是使偏差朝减小的方向调整，这一朝新平衡方向发展的河流趋向或基本特性，称之为冲积系统的“趋衡性”或“趋衡响应原理”。在假定外部扰动发生概率符合泊松分布及单个扰动响应强度满足指数衰减率的基础上，给出了定量描述非平衡态河流趋衡响应过程的初步模型形式。基于美国多座水库下游河道实测数据的规律性检验表明，冲积系统对扰动的响应强度随时空推移呈非线性衰减趋势，整个过程从数学上服从统一的理论曲线，体现了河流演变的时空趋衡性。(2)考虑水流驱动力和床面阻尼力反映影响床面泥沙运动状况的两个矛盾方面，以床沙起动流速与弗劳德数之比作为定量描述趋衡衰减系数α/v的河流动力学参量，明晰了非平衡态河流时空趋衡响应速率的影响因素，建立了水库运用后枢纽下游河道河床累计冲刷深度的定量预测方法，在黄河三门峡水库下游沿程冲刷模拟中取得了良好效果，为冲积河流非平衡态时空调整过程的预测提供了新方法。(3)运用构建的冲积系统趋衡响应模型，对黄河中游古贤水利枢纽拦沙运用后下游河道沿程冲刷及潼关高程下降引起的渭河下游段的溯源冲刷进行了预测计算。结果表明，龙门和潼关的河床累计冲刷深度分别为1.84 m和1.43 m，华县、渭南两站溯源冲刷深度分别为0.54 m和0.25 m，与采用卜海磊方法计算的结果基本一致，但本文方法给出的冲刷剖面相对更符合实际，可供相关工程决策参考。