让智慧之花在指尖上绽放
——浅谈小学数学实验教学

2022-12-05 09:42朱秋婉

新课程 2022年35期

朱秋婉

（福建省龙溪师范学校附属小学，福建漳州）

“智慧的鲜花是开放在指头尖上的”，表明动手操作的重要意义。新课标也指出，高效的数学学习活动不是仅仅依赖模拟和记忆，而是要让学习者自己实践、独立探究、合作互动，让学生体验数学知识的再发现、再创造的过程，让学生有深刻的学习体验，促使学生逻辑思维和情感意识的和谐发展，充分开发学生的潜能。小学阶段数学实践是数学活动的主体，而数学实验又是数学实践的重要组成部分。那何为数学实验呢？

数学实验，是指为了证明某个数学猜想、分析掌握某些数学基本原理、解决某些数学实际问题，而在形象具体的实验环境中以及一定的实验要求下，开展综合性的数学探究活动。而数学实验教学，则是指通过数学实验，指导学习者参加实践、独立探究、协作交流，进而发现并提出问题、证明猜想、理解掌握数学基本原理、解决数学实际问题的教学活动。数学和其他学科的同样要通过观测与试验来发现和检验，和其他学科的区别在于，数学实验所面临的对象并非物质材料，而是如图形、数据等的非物质材料。本文我将通过对案例的分析向大家展示数学实验教学的途径和方法。

一、实验中验证猜想

案例一：掷硬币——实验体验等可能性

（一）分析猜测

师：掷硬币，正面朝上一方为胜，而反面朝上另一方胜，公平吗？谁能说明道理？

生：公平。由于硬币有二面，落地后要么正向朝上，要么反向朝上，所以公平。

师：如果再多掷几次，猜猜正面朝上与反面朝上的次数会如何？（接近）这只是大家的猜想，咱们来试验一下。

（二）动手实验

课件出示规则，四人学习小组进行分工：

1.选一人任记录员（用画“正”法记录），另一人当监督员。

2.其他二人掷硬币，每人5次。（硬币要从50厘米左右的高度落下。）

活动记录卡：

学生动手试验，记录数据。

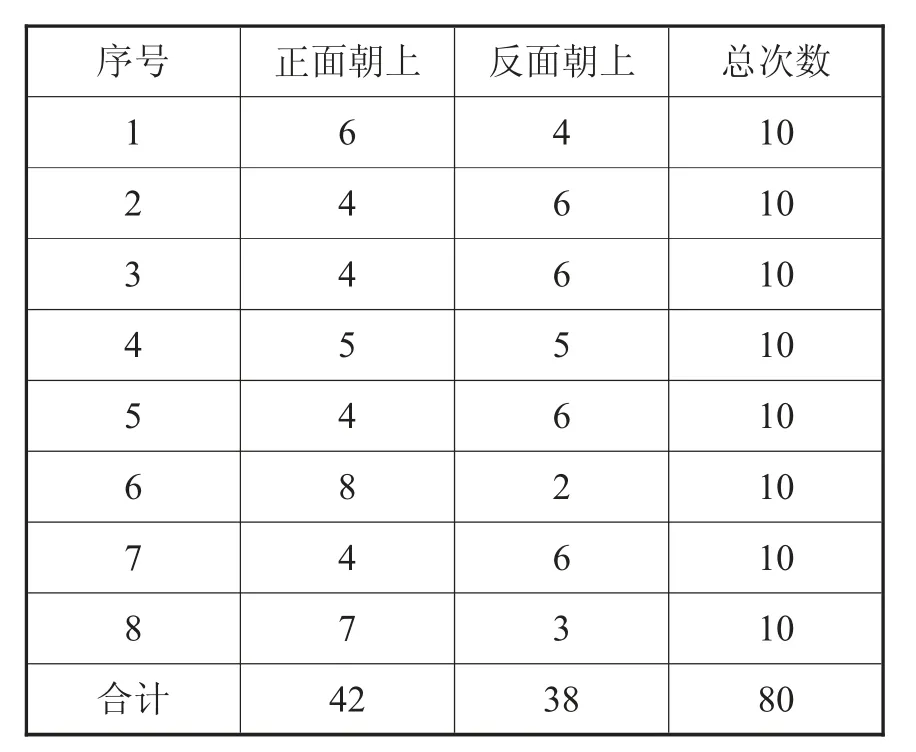
反馈：各小组汇报实验数据。

活动记录卡（汇总）：

师：请同学们仔细观察各组正面朝上和反面朝上的数据，你发现了什么？

生1：我发现有的组掷到正面的次数比掷到反面的次数多，有的组正面的次数比反面的次数少，有的组正反面次数同样多。

师：有的组掷到正面的次数比反面的次数多，多很多吗？

生2：多一些。

生3：我发现有的组出现正面是8，反面是2。

师：这种情况出现得多吗？

生：不多。

师：对了，这是很偶然的现象。

师：也就是说从各组的实验结果和汇总的数据上看，正反面的次数还是相当（接近的）。假如实验再继续下去又会出现什么情况呢？

每组各掷50次硬币，汇总数据之后，学生观察汇总数据发现正反面朝上的次数很接近。

师：如果再实验下去呢？

学生大胆猜测：硬币正面朝上的次数和反面朝上的次数会越来越接近。

【课件展示】

师：这是五位数学家经过成千上万次掷硬币的试验结果。再看一下正面朝上和反面朝上的次数是不是如你们猜测的那样？

生：正面朝上和反面朝上的次数非常接近。

师：掷硬币的次数越多，正反面的次数就越接近，最后趋向相同。

师：那掷一枚硬币，第一次正面朝上，第二次必定反面朝上吗？

生：不一定。

师：对了，硬币落地具有偶然性，但是随着实验频次的增多，正反面出现的次数会越来越接近，最终趋向相等。可见，偶然中有必然。

案例二：体积单位间的进率

学生在学习了“体积”，认识并建立1m3、1dm3、1cm3的体积单位的概念之后，继续探究体积单位间的进率。在问题情境中，学生有了认知冲突，产生疑问：“1dm3的模具里究竟能装下多少个1cm3的小正方呢？”我让学生拿出1dm3和1cm3的模具，仔细比对、大胆猜测。

生1：我觉得1dm3里最多能装下100个1cm3。

生2：我猜50个。

生3：不对，没那么少，应该有500个。

生4：我觉得有1000个……

基于学生的年龄特点和认知水平，学生的空间想象能力还是存在较大的差异。此时数学实验活动的必要性呼之即出。在实践操作中，多数的学生在1dm3的模具中用1cm3的小正方体摆满最底层就发现有100个了，观察推理1dm3的模具中能摆这样的10层，所以1dm3=100×10=1000cm3，继而推理出1m3=1000dm3。当然也有空间想象能力较好的学生，只用28个1cm3的模具就能实验得出1dm3=10×10×10=1000cm3。

以上两个案例都是通过数学实验验证学生的猜想，在问题情境中较好地激发学生学习的内驱力。案例一中掷硬币的试验次数从少到多，环环相扣，层层递进，引导学生循序渐进并进行大胆猜测，充分调动了学生的探索激情、激发学生实践的欲望。学生在实验中逐步验证自己的推测，教师再适时地将科学家的实验数据加以补充拓展，让学生明确“硬币落地具有偶然性，但是随着实验频次的增多，正反面出现的次数会越来越接近，最终趋向相等。偶然中有必然。”等可能性核心思想。而案例二在实验过程中虽然不需要复杂的运算和推导，只要动手操作、实践与观察就能得出结论，虽然只是简单的实验操作，但就如一句名言：“我做过了便真正理解了!”效果比教师直接说教要好得多。

二、实验中理解公式

案例三：圆的周长公式

师：请同学们利用绳子、尺子等工具测量课前搜集的生活中的圆的周长。

学生明确操作要求，并尝试用滚动法、绕圈法、用软尺测量等方法测量，并汇报结果，提出问题。

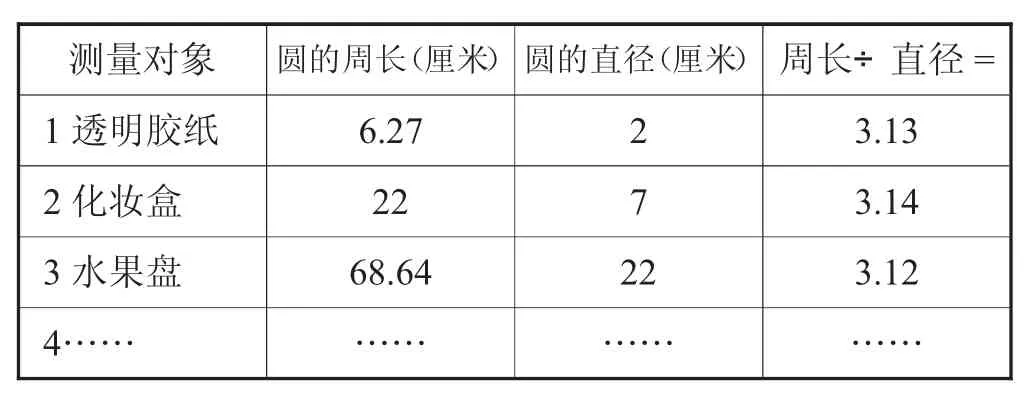
师：同学们都认为圆的周长与它的直径有关，那到底有什么关系呢？咱们来做个实验，请测量出你们所收集的圆的周长和直径，并算出周长除以直径的商，完成下表：

交流实验结果，得出结论。

师：观察同学们汇报的数据，你们有什么发现？

生：圆的周长÷直径都不是整数。

师：其他小组有不同意见或补充吗？

生：圆的大小虽然不一样，但我们算出每个圆的周长也都是直径的3倍多一些。

师：有同样发现的小组请举手。

师：这表明圆的周长除以直径的商是有规律的。刚才我们所测量的这些圆中，每个圆的周长都是直径的3倍多一些。那其他的圆是不是也有这样的规律？课件演示。

生：的确是这样。

师：我们测量了大小不同的圆，但却有相同的发现。（圆的周长是它直径长的3倍多一些）

师：圆的周长大约是它的直径的3.14倍，3.14叫作圆周率，很早以前我国的数学家就发现了圆周率，那圆的周长公式是？

生齐答：圆的周长=直径×3.14

本案例中我用心做好实验前期准备，课前让学生备好软尺，软尺既有尺子的功能又具备了线的特点，既能提高实验的速度，又可以减少实验误差。课前我还让学生搜集日常生活中不同的圆，大大丰富了实验素材，拓展了实验的空间，发散学生的研究思路，也使实验数据更有说服力。案例中我为学生提供了数学实验的时间和空间，对学生实验的方法进行深入细致的指导，提高实验的准确度。在操作前确定操作方法、操作要求以及操作的注意事项，然后学习小组合作进行实验，探索圆周长和直径的比值规律，认识圆周率，体验圆周长公式的由来，经历了知识再发现、再建构的过程。数学实验可以帮助学生从本质意义上去理解数学，掌握数学公式。

三、实验中解决问题

在实际教学中通过数学实验解决数学问题的类型很多，比较典型的还是在解题过程中的应用，如以下两例：

案例四：

下面四个图形中，（）是由

案例五：将一条长20米的绳子连续对折3次后的长度是这条绳子的几分之几？如果连续对折3次后，从中间剪开，最长的一段绳子是多少米？

这两道题对五年级的小学生而言，仅凭想象是很难正确解题的，尤其空间想象力差的学生就更吃力了。通过测试我发现半班以上的学生做错，部分做对的学生也是懵的，并没有完全理解。我适时提问：“谁有好办法能帮助学生正确解决这样的问题？”学生陆陆续续介绍了几个推理方法，但仍有一部分学生眉头紧锁，实在是太难想象了!生：“那我们就请数学模具来帮忙，做个实验”“数学模具从哪里来？”“马上做一个!”“好办法!”我拿出了一张白纸描题目中带点的三角形并剪下来。拿着这个实验用具转一转，答案不就出来了吗？学生们都会心地笑了，每个学生都自发动手制作模具，拿着模具绕着中心点旋转，很快学生就发现有规律可循。“如果这时候不借助这个实验用具，你们还能找出正确答案吗？”“能!”学生非常自信地答道。看来学生已在数学实验中建立了空间观念，锻炼了想象能力。有了这种题目的解题经验，对于案例五出现想象不出来难以解答的时候，学生自然而然就想到了实验法。有的学生找来身边的小绳子，没有小绳子的学生就用草稿纸捻出一条长长的纸条，也操作起来。再难的题目，在学生的实验操作中，都迎刃而解。学生不但得到了“鱼”，也得到了“渔”!在数学实验中，学生学到了学习方法，并灵活地运用这些方法解决实际问题，个个都很棒。

这就是数学实验教学的核心目的：发展学生多方面的能力，让学生掌握学习方法，并能灵活地运用这些方法解决实际问题。