课程视域下的数学单元作业重构
——以指数函数、对数函数的图象与性质复习课为例
韦庆贺
(江苏省连云港市厉庄高级中学 222121)
1 引言
《学记》中说“时教必有正业,退息必有居学”,其中“居学”指课外作业,作业是达到“学以致用”和“以用促学”的重要手段.在教学过程中,为保证学生掌握知识的持久性和提升知识运用的灵活性,很多教师无力采取其他途径,只有通过大量、重复的作业训练,让学生收集各种题型,以缓解学生在考试过程中面对新题型而产生的陌生感.随着课程改革的进一步深化,如何利用作业提升教学质量和促进学生发展是一线教师亟待解决的问题.2019年国务院办公厅印发了《关于新时代推进普通高中育人方式改革的指导意见》,提出提高作业设计质量,精心设计基础性作业,适当增加探究性、实践性、综合性作业.作业设计要从学习活动整体考虑,系统、科学、合理设计不同层次的作业,引导学生自觉预习、及时整理和巩固所学知识,养成良好的学习习惯.
2 单元作业有关概述
单元作业是为某个教学单元所设计的所有作业的总和.合理的单元作业应具有整体性、结构化和进阶性的特点.单元作业可以增强同一单元不同课时作业之间的结构性和递进性,减少一些仅仅针对低水平目标、反复操练性质的作业,进而留出时间增加发展高阶思维、关键能力的作业比例,有助于发展学生的学科核心素养.
3 单元作业重构的教学实践
根据课堂内容设计单元作业,本节课内容 为高三复习课:指数函数、对数函数的图象与性质.
3.1 教学目标
(1)理解指数函数、对数函数的图象和性质;
(2)能够利用指数函数、对数函数的图象和性质解决比较大小,会用研究函数性质的一般方法研究简单的复合函数性质;
(3)解决简单的含参复合函数、抽象函数不等式恒成立及存在性、函数零点等问题,体会从特殊到一般、数形结合、函数与方程等数学思想方法,发展学生数学运算、直观想象、逻辑推理等数学核心素养.
3.2 教学重点和难点
本节课教学重点和教学难点主要体现于两个层面:一是掌握指数函数、对数函数的图象与性质,会应用函数性质解决简单问题;二是解决不等式恒成立、存在性等问题的常用方法,会运用数形结合、函数与方程等思想方法解决问题.
3.3 教学过程

设计意图此题入口宽,回顾指数函数、对数函数的图象和性质,回顾解决不等式存在性问题及恒成立问题的常用方法,激活学生思维.
例题已知函数f(x)=ax+bx,其中a>0且a≠1,b>0且b≠1.
(1)请写出一组数对(a,b),使函数f(x)为偶函数.
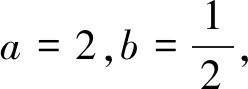
设计意图第(1)问以两个指数函数“叠加”形式呈现,给学生一个相对陌生的情境,并用“例题”的形式给出,是学生相对陌生的设问情境,激发其探究欲望,帮助回顾研究函数性质的基本方法.第(2)问以“结构不良”的形式设问,是新高考中的常见题型,不同的学生根据自身认知结构选择条件尝试解决,掌握解决复合函数方程根的问题、不等式恒成立问题、不等式存在性问题的常用方法与基本数学思想.
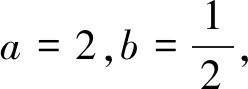
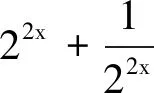
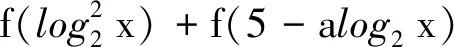
设计意图将研究对象f(x)=ax+bx为偶函数改为研究f(x)=ax-bx为奇函数,结构形式上的相似及研究方法的相似,能较好地保持学生思维的连续性,使其思维处在高阶状态.但此变式并没有给出具体的a,b的值(这也是此题的另一个难点),这需要学生调动研究抽象函数不等式问题的常用方法——转化为“作用对象”大小关系问题.渗透类比思想、转化与化归思想,培养学生的逻辑推理、数学抽象等数学核心素养.
3.4 课堂小结
(1)指数函数、对数函数的图象与性质;
(2)利用函数性质解决相关方程有根(或函数存在零点)、不等式有解或恒成立问题的方法与思想;
(3)解决函数问题,特别要关注数形结合、化归与转化、分类讨论思想的应用.
4 单元作业重构中的几个原则
4.1 合理设计基础性作业
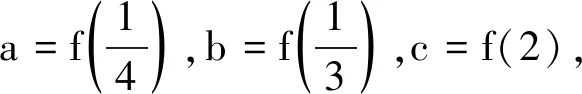
A.a C.c 题目来源及意图作业1和作业2来源于人教A版《普通高中教科书高中·数学(必修第一册)》复习参考题4,这两道题旨在帮助学生回忆指数函数、对数函数的图象和性质,并利用单调性进行比较大小、求值域等,体现作业的基础性原则,对应教学目标(1). 教材是课程实施的重要载体,是教师设计作业的重要依据,明确教材中单元学习的目的和任务,并以此为标准设计整个单元的作业体系,才能确保作业设计不超纲、不走样. 4.2 科学设计巩固性作业 作业3:设函数f(x)=ln|2x+1|- ln|2x-1|,则f(x)( ). 作业4:已知函数f(x)=2x+x,g(x)= log2x+x,h(x)=x3+x的零点分别为a,b,c,则a,b,c的大小顺序是. 题目来源及意图作业3来源于教辅精选,考查复合函数性质的一般研究方法.作业4来源于人教A版《普通高中教科书高中·数学(必修第一册)》复习参考题4,考查函数与方程、数形结合的思想方法,这两题体现作业的巩固性原则,对应教学目标(2). A.f(x)为奇函数,g(x)为偶函数 D.函数f(x)与g(x)既无最小值,也无最大值 A.函数f(x)为偶函数 B.当a>1时,函数在f(x)在(0,+∞)上为减函数 题目来源及意图作业5和作业6来源于教辅精选,考查研究复合函数性质的一般方法、数形结合思想等,与课堂例题相匹配,体现作业的巩固性原则,对应教学目标(2)、(3). 4.3 适度设计拓展性作业 题目来源及意图作业7为教辅改编题.本节课课堂上没有出现“迭代函数”的相关例题及处理方法,但本题是一个利用数形结合解决问题的典型问题.设计在作业中,可以给部分优生一个自主探索发现的机会,并在此过程中进一步感悟数形结合思想,体现作业的拓展性原则,对应教学目标(3). 4.4 优化设计综合性作业 作业8:设函数f(x)=log2(4x+a·2x-1),x∈[0,1]. (1)若a=1,求方程f(x)+x=0的根; (2)若方程f(x)+x=0在[0,1]上无实数根,求实数a的取值范围. 题目来源及意图作业8为教辅改编题,此题考查指对数运算、指对数函数的性质、恒成立问题、方程根的存在性问题等.问题分析和解决过程,体现了作业设计中注重方法指导、思维过程的表达与交流等功能,对应教学目标(3). 4.5 创新设计新情境作业 作业9:对于定义在[p,q]上的函数m(x),设x0=p,xn=q,用任意的xi(i=1,2,…,n-1)将[p,q]划分成n个小区间,其中xi-1 |m(x0)-m(x1)|+|m(x1)-m(x2)|+…+ |m(xn-1)-m(xn)|≤M 恒成立,则称函数m(x)为在[p,q]上的有界变差函数. (1)证明函数f(x)=2x+2-x是在[0,2]上的有界变差函数,并求出M的最小值; (2)写出一个f(x)在[p,q]上是有界变差函数的充分条件,使上述结论成为其特例(不要求证明). 题目来源及意图作业9改编自2021年上海市期末考题,是一个“新定义”情境下的问题.首先,要熟悉函数f(x)=2x+2-x的性质(这是对课堂内容的回顾),其次需要从题干信息中分析出M的求法,考查学生数学抽象、数学运算、逻辑推理等核心素养,对应教学目标(3). 在强调作业“减负增效”的背景下,教师应当转变观念,科学评估作业质与量的关系.数学单元作业重构应贯彻全面育人理念,关注学生核心素养的养成,关注学生个体间的差异,关注各学科各阶段作业量,关注五育教育融合,助力每位学生全面发展.