基于成本-效益的超多车道高速公路左侧硬路肩设置条件
林小媛, 朱顺应, 李维吉 , 肖文彬, 王 红
(1.深圳市综合交通与市政工程设计研究总院有限公司, 广东 深圳 518003; 2.武汉理工大学 交通学院, 湖北 武汉 430063)
0 引言
我国早期的高速公路建设以双向四车道为主,近年来随着车辆的快速增长,许多高速公路为满足通行需求,已改扩建或正改扩建为双向八车道以上。在超多车道高速公路中,我国因土地有限,左侧硬路肩是否必要设置成了久争不休的话题。
左侧路肩为内侧车道高速行驶的车辆提供侧向净空、容错空间,作为救援车辆的应急车道,同时为内侧车道上发生故障、养护维修车辆提供临时停靠的场所,避免内侧车道上出现故障或耗尽燃料的车辆穿过多条车道至右侧路肩的过程中引发交通事故。ZHONG[1-2]等运用可接受间隙理论和交通仿真方法,从运行效率和交通安全2个方面分析了左侧硬路肩设置的必要性。胡祖敏[3]等发现高速公路互通单车道匝道设置左侧硬路肩可有效预防互通匝道交通事故。美国地广人稀,《公路和城市道路几何设计》[4]规定高速公路两侧都必须设置路肩,因此国外对路肩的研究主要集中在车道布设、使用模式、拥堵缓解等方面。 KITALI[5]等研究左侧路肩宽度对最内侧车道安全性影响,发现更宽的路肩能显著降低最内侧车道事故率。KAY[6]等发现宽路肩能增加内侧车道的通行速度。MA[7-8]等研究表明,临时硬路肩的动态使用,可以增加拥堵时高速公路通行能力。
以上研究文献,只提出了左侧硬路肩设置必要性和作用,并未明确提出设置左侧硬路肩的条件。因国内现有规范条例中,对左侧硬路肩的设置无强制要求,没有相关研究成果作为理论支撑,且改扩建高速公路考虑了设置左侧硬路肩所增加的用地成本,自国内2002年第一条双向八车道沈大高速改扩建以来,几乎所有已完成改扩建的多车道高速公路(沪宁、广佛等)都未设置左侧硬路肩。基于左侧硬路肩在超多车道高速公路中的重要作用,有必要为其提供设置判据。
成本-效益法常用于工程建设依据。唐敏[9]等对交通诱导电子信息屏进行社会效益、经济效益综合评价。SUN[10]等对先进视频监控系统环境下,高速公路服务巡查进行成本-效益评价。目前国内外主要采用成本-效益法比选工程建设方案,本文基于成本-效益法提出了改扩建超多车道高速公路左侧硬路肩设置判别算法,设计了左侧硬路肩的效益计算指标。
判别算法中的成本考虑建设左侧硬路肩的预期投资,效益通过建立总事故预测模型,运用美国NCHRP研究左侧硬路肩宽度与事故的修正系数得到可减少事故计算带来的社会效益。事故预测方面,综合国内外文献,广义线性模型因可揭示因果关系,适用范围广且误差小,被国内外学者普遍认可,并经常使用于交通事故预测中。王迎[11]等基于广义线性模型建立了高速公路交通预测模型。马壮林[12]等基于零堆积负二项回归建立了路侧事故数预测模型,发现交通量、货车比例、车道数、曲线比例、曲度和平均纵坡等因素,对路侧事故有显著影响。HYODO[13]等利用广义线性模型,分析交通因素对事故风险的影响,结果表明拥堵流态、混合流态、大型车辆比例,显著增加了严重和致命事故的风险。
处理非线性问题通常有2种方法,一是直接拟合广义线性模型,二是先进行数据变换再进行拟合。以上文献均直接拟合广义线性模型来预测交通事故。很多时候,原始数据很难满足线性模型假设前提,需要对原始数据进行变换,保留线性、正态性特征且不丢失信息。故本文采用Box-Cox对变量进行非线性变换再构建事故预测模型。对于交通事故影响因素,综合国内外文献,及考虑到本文研究为中宏观对象,故从道路和交通条件方面选取相关自变量进行模型构建。
本文以广深高速为例,针对超多车道高速公路左侧硬路肩是否设置提出成本-效益判别算法,基于Box-Cox变换构建事故预测模型,联系左硬事故修正系数计算效益,旨在为改扩建的高速公路设置左侧硬路肩,从经济方面提供一种切实可行的判别方法,以期完善设计规范提供一个依据。
1 左侧硬路肩建设成本
国务院2015年颁布的《收费公路管理条例》对不同投资主体收费公路的收费期限进行了规定,最短的为15 a,最长的不得超过30 a。《公路工程技术标准》(JTG B01-2014)规定“高速公路的设计交通量应按20年预测”。结合这2点,本文把改扩建的投资使用年限定为20 a。
超多车道高速公路桥梁段增设左侧硬路肩估计造价为a万元/km,路基段增设左侧硬路肩估计造价为b万元/km,改扩建路段的拆除成本为c万元/km,改扩建的建设年限为t1,社会折现率为is,为简便计算,建设成本为建设期内等额投资,Csum折现到建设末年的计算公式:
(1+is)t1m
(1)
式中:Csum为路段折现到建设末年的总投资,万元;Lbridge为路段桥梁长度,km;Lsubgrade为路段路基长度,km;Ldismantle为拆除长度,km;t1为建设持续年限;t1m为建设末年与建设年的年数差,a。
2 左侧硬路肩效益
2.1 效益分析
设置左侧路肩的经济效益,本文只考虑在设置左侧路肩后、因减少交通事故而获得的社会经济效益。
2.1.1事故损失组成
因为受到事故发生形态、严重程度、波及范围等因素影响,事故损失精确测算比较复杂,为了降低交通事故成本测算的难度,这里仅对3个比较大的方面进行考虑,主要包括:① 事故伤亡者相关的经济损失;② 事故造成的车辆、货物以及路产损失;③ 事故造成的交通延误损失[14]。
a.伤亡人员的经济损失。
交通事故中死伤人员,其损失为生命消失事件本身的损失和从事故致死的时间到预计寿命之间的社会未来期望收入值的现值之和,事故中受伤人员经济损失计算式如下:
(2)
式中:W1为死亡者的经济损失,万元;X为生命消失事件本身的损失,同一时期每个人相同,用上年度人均GDP的20倍测算,万元;Y为该年度平均每人的国内生产总值,万元;q为折现系数,折现率+1;g为国内生产总值增长系数,增长率+1;n1为工作能力降低时间,即死亡年或受伤年与预期寿命年的年数差,a;暂时性致残,n1平均为5a;e为伤残等级系数,死亡e=1,终身致残e=0.43,暂时性致残e=0.25;n2为平均不能工作时间,d;250为全年扣除节假日后的正常工作日,d。
b.事故导致的路产、车辆财产损失。
路产损失主要是交通事故导致的道路设施损坏、因车辆着火爆炸等引起的路面污染及损坏,车辆损失主要是事故车辆本身以及车上的财产损失:
W2=U+Z+S+T
(3)
式中:W2为路产和车辆损失,万元;U为道路设施损坏造成的损失,万元;Z为路面损失,万元;S为机动车损坏的直接损失,万元;T为车辆上的财产损失,万元。
c.交通延误损失。
交通延误损失主要是指交通事故造成的车辆延误或者车辆绕行改道使得旅客或者运送的货物在途时间增加需要支出的成本。旅客在途时间增加所造成的损失为创造国民收入的减少,货物在途时间增加使货物占压的资金利息增加,计算式如下:
(4)
而货物在途时间价值等于货物平均价格与银行贷款付息率的乘积:
(5)
式中:ACP为货物平均价格,万元;IR为贷款付息率,%。
未来使用年限内每年单起相关事故效益计算式如下:
W(i)=(W1+W2+W3)×(1+is)-(t2i-t1)
(6)
式中:W(i)为未来使用年限内,第i年单起相关事故效益,万元;is为社会折现率,%;t2i为使用年与建设末年的年数差,a,建设开始年为交通事故预测基年。
2.1.2路肩宽度修正系数
根据左侧硬路肩的主要功能,不设置左侧硬路肩的多车道高速公路上,易发生如下几种交通事故:① 内侧车道上有轻微故障或燃油耗尽的车辆,因没有临时停靠场所而需要换道至右侧硬路肩过程中引发的事故。② 内侧车道上发生交通事故车辆无法及时转移至路肩导致的二次事故。③ 内侧车道上发生的撞中央分隔带事故。这3种事故按涉及车辆的数目将①②两种事故分为多车事故,第③种事故分为单车事故。
左侧硬路肩宽度会影响其预防事故数,国内尚未有修建左侧硬路肩高速公路事故数据,因此参考美国NCHRP中定义的CMF系数:高速公路左侧硬路肩宽度修正系数。根据相关左侧硬路肩宽度可以计算出能够减少的事故发生频率。计算公式如下:
CMFi=exp[a×(Wis-6)]
(7)
式中:CMFi为高速公路左侧硬路肩宽度修正系数;a为回归系数;Wis为左侧硬路肩宽度,f t;基本条件是6 f t的左侧硬路肩宽度(1f t≈0.3 m)。
左侧硬路肩宽度修正系数分成4类,分别是与左侧硬路肩相关的多车事故中的有人员伤亡和仅财产损失关联系数,单车事故中的有人员伤亡和仅财产损失关联系数,参数说明如表1所示。
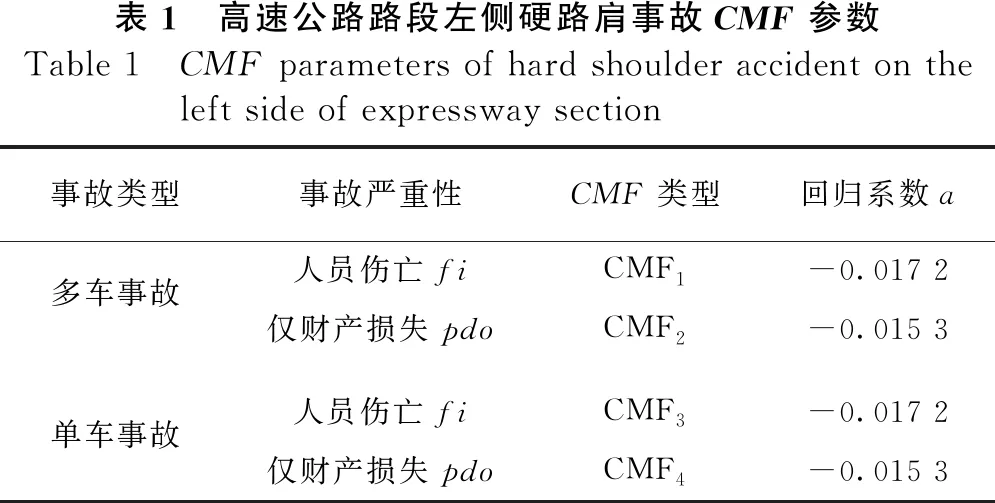
表1 高速公路路段左侧硬路肩事故CMF参数Table 1 CMF parameters of hard shoulder accident on the left side of expressway section事故类型事故严重性CMF 类型回归系数a多车事故人员伤亡fiCMF1-0.017 2仅财产损失pdoCMF2-0.015 3单车事故人员伤亡fiCMF3-0.017 2仅财产损失pdoCMF4-0.015 3
根据我国《公路路线设计规范》(JTG D20-2017)中规定:高速公路整体式路基双向八车道和以上路段宜设置左侧硬路肩,其宽度应不小于2.5 m,左侧硬路肩宽度包含左侧路缘带宽度。
根据不同左侧硬路肩宽度可以计算出相应的CMF值,得到相应左侧硬路肩宽度下可以减少的事故率,进行左侧硬路肩的设置效益计算。
2.2 事故预测模型
2.2.1影响因素
影响左侧路肩的多车事故和单车事故的因素主要分为主观因素和客观因素,驾驶员的思维过程和倾向性为主观因素,但究其缘由,驾驶员的判断也是受客观因素的影响。道路线形能影响视距,道路车流拥挤程度将影响车辆跟驰距离,因此本文在借鉴国内外的相关研究基础上,对于未设置左侧硬路肩引发的多车事故和单车事故仅考虑路段宏观客观因素,从路段交通流、道路环境中选取相关自变量进行研究。
a.路段转向平均交织程度。
高速公路互通间车辆基于目的地的变道会产生交织,出现交通流线间的分流点、合流点和冲突点。随着车道数的增加,交织程度也越复杂,变道车辆受周围车辆的干扰会增强。
交织区交通流图如图1所示。
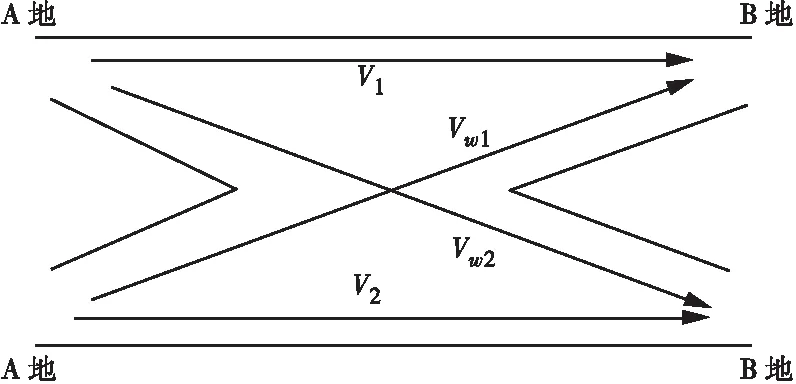
图1 交织区交通流
则平均交织程度计算公式如下:
(8)
式中:Vw=Vw1+Vw2,为交织区段中的总交织交通量,pcu/h,Vw1,Vw2为两交织流中的交织交通量,pcu/h;V=V1+V2+Vw,为交织区段中的总交通量,pcu/h;L为互通间长度,km。
b.货车比例。
货车比例计算公式如下:
(9)
式中:Vtruck为路段上货车标准交通量,(pcu/h);Vsum为路段上总交通量,(pch/h)。
c.路段v/c比。
路段v/c比是在理想条件下,最大服务交通量与基本通行能力之比,其计算公式如下:
(10)
式中:v为高速公路在规定服务水平下的最大服务交通量,(pch/h);c为规定服务水平下的基本通行能力,(pch/h)。
d.曲线比例。
曲线比例指各路段中平面曲线的长度占路段总长度的比值。
(11)
式中:Lping为路段中平面曲线的长度,km;Lsum为路段总长度,km。
e.平面线形均衡指标。
平面线形均衡指标又称平面线形偏转指标,表征路线的弯曲程度(路线弯曲影响行车舒适性),按下式计算:
(12)
式中:αi为道路曲线偏转角,rad;L为路段长度,km。
f.纵断面线形指标。
纵断面线形指标主要考虑累积相对势能变化指标:
(13)
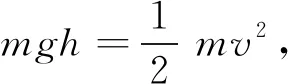
g.车道数。
车道数即路段包含的车道数,用x7表示。
2.2.2数据的Box-Cox变换
高速公路交通事故是由于多种因素引起的,在统计分析中最常用的一般线性模型为:
Y=Xβ+ε
(14)
式中:Y为反应变量矩阵;X为自变量矩阵;β为估计参数矩阵;ε为随机误差。
当ε服从正态分布时,模型达到最优,但通常会遇到因变量分布不满足正态分布的情况,这时一般线性模型不能直接应用于数据分析,且众多研究结果表明,高速公路交通事故数与各影响因素之间并不能用简单的线性关系描述[15]。Box-Cox变换是一种常用的非线性变换,通过引入一个最优的λ参数,使得变换后的回归模型满足线性、独立性、方差齐性,以及正态性的同时又不丢失信息。
对不同的λ,Box-Cox变换表达式如下:
(15)
Box-Cox变换最重要的是确定最优的λ,采用最大似然估计方法来确定λ。对固定的λ,令:
(16)
RSS(λ,Z(λ))=Z(λ)T(I-XT(XTX)-1X)×
Z(λ)
(17)
为了求lnLmax(λ)的最大值,只需求残差平方和RSS(λ,Z(λ))的最小值。虽然很难找出RSS(λ,Z(λ))最小值点λ的显式解析式,但对一系列给定的λ值,通过线性回归模型的最小二乘估计,很容易计算出相应的RSS(λ,Z(λ))值。画出RSS(λ,Z(λ))关于λ的曲线,从图上可以近似地找出使RSS(λ,Z(λ))达到最小值的λ。
2.3 总效益计算
设置左侧硬路肩带来的预期总效益计算式如下:
W(i)×(1+is)-t2i
(18)
式中:Wsum为设置左侧硬路肩带来的预期效益,万元;t2为建成后的预期使用年数,a;Yij(i=1,2,…,20,j=1,2)为预测建成后第i年第j种事故(1为多车事故,2为单车事故)的预测事故率,(起/km);Lk为各互通间长度,km(k=1,2,…,25);W(i)为未来使用年限内第i年单起相关事故效益,万元。
3 左侧硬路肩设置条件算法
本文运用成本-效益法设计左侧硬路肩设置条件算法,步骤如下:
① 设置左侧硬路肩预期投资Csum分析。
② 分析左侧硬路肩可预防的事故类型,以及设置左侧硬路肩宽度修正系数CMF。
③ 运用Box-Cox非线性变换建立事故预测模型,联系左硬宽度修正系数CMF,计算设置左侧硬路肩的预期效益Wsum。
④ 建立左侧硬路肩设置指标:
(19)
K≥1时,建议设置左侧硬路肩。
⑤ 运用算法得出的设置方案与不设置硬路肩以及全设置硬路肩进行整体效益评价。
整体效益评价引入内部收益率iIRR作为指标进行判别,构建方程通过线形插值法求解如式(20)、
式(21)所示。内部收益率大于折现率则方案通过,收益率越高方案总效果越好。
NPV(iIRR)=
(20)
iIRR=iIRR-1+
(iIRR-2-iIRR-1)
(21)
式中:NPV为净现值,W(i)为未来使用年限内第i年单起相关事故效益;Csum为设置方案总投资成本;iIRR-1与iIRR-2为NPV(iIRR-1)<0且NPV(iIRR-2)>0的取值。
流程如图2所示。
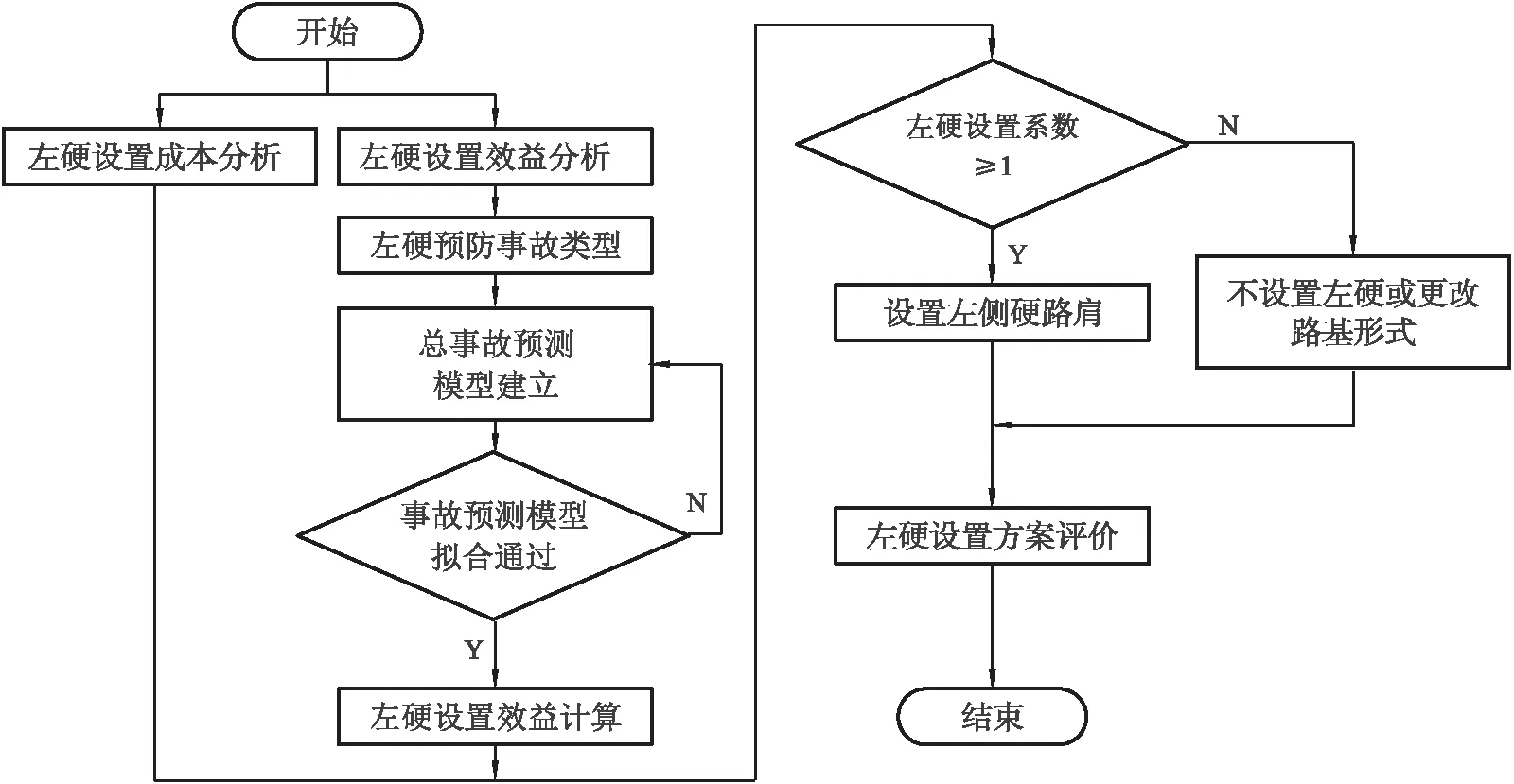
图2 经济效益法分析流程
4 实例分析
即将进行改扩建的广深高速公路设计速度120 km/h,整体扩建为双向十车道,部分互通(如太平-五点梅)扩建为双向十二车道,运用本文所提出算法进行左侧硬路肩设置判断。对于折现率,史富文[16]参考资本的边际社会机会成本测算后,发现我国目前的社会折现率调至5%~7%。根据国家数据统计,20 a内我国的社会折现率无大变化,平均折现率为7%,且随着经济增速的减缓,社会折现率呈现逐渐减小的趋势。故本文所用2017—2019年的平均社会折现率取值为7%,2020—2045年的平均社会折现率取值为6%。
4.1 成本
广深高速桥梁段增设左侧硬路肩估计造价为4124万元/km,路基段增设左侧硬路肩估算造价为1 546万元/km,预期建设年限为5 a。
以新塘-麻涌互通为例,该段总长5.44 km,桥梁段占0.415 km,路基段占5.025 km,沿线拆除成本1 404.74万元,由式(1)计算可得该段扩建成本如下:桥梁段1 711.46万元,路基段7768.65万元,拆除成本1 404.74万元,每年投资2 176.97万元,总成本13 008.11万元。
4.2 效益
4.2.1事故损失效益计算
2017—2019年中国人均GDP为6.56万元,人均国内生产总值6.53万元,人均寿命77岁,折现系数1.07,增长系数1.067,多车事故平均伤亡年龄35岁,伤亡3人,单车事故平均伤亡年龄41岁,伤亡1人。旅客在途时间价值为35元/(h·人),货物在途时间价值为800元/(h·t),根据所统计到的广深高速各互通之间的交通事故数据,发生多车事故导致的平均延误时间为1.72 h,单车事故导致的平均延误时间为0.8 h。
根据上文提出的事故成本计算方法,计算2017—2019年各互通人员伤亡和仅财产损失的多车事故/单车平均事故成本,定为基年事故成本,如表2所示。
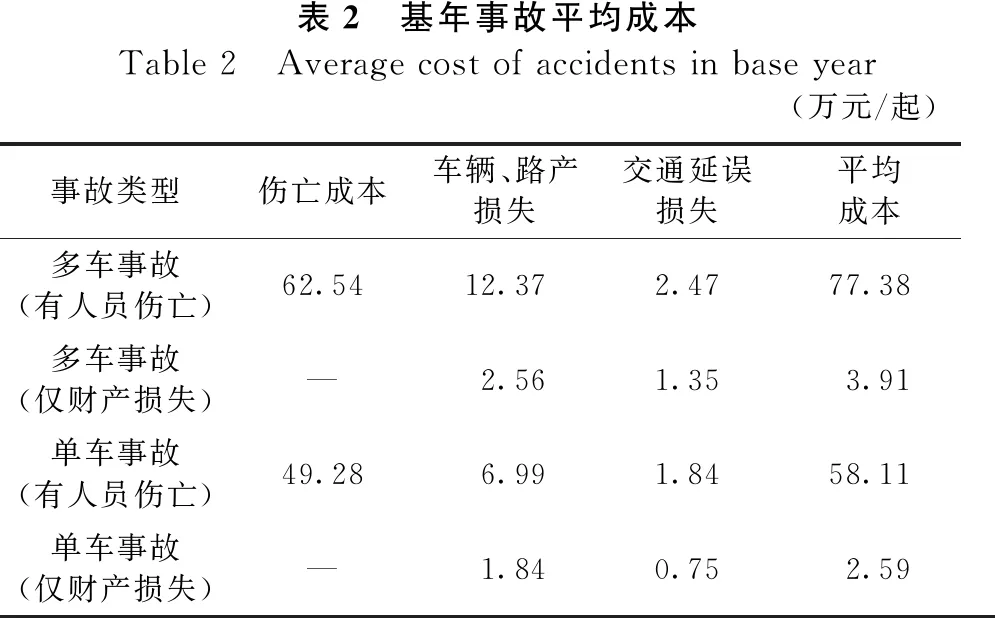
表2 基年事故平均成本Table 2 Average cost of accidents in base year(万元/起)事故类型伤亡成本车辆、路产损失交通延误损失平均成本多车事故(有人员伤亡)62.5412.372.4777.38多车事故(仅财产损失)—2.561.353.91单车事故(有人员伤亡)49.286.991.8458.11单车事故(仅财产损失)—1.840.752.59
4.2.2CMF值
广深高速现状及未来不设置左侧硬路肩时的左侧余宽为1.25 m,换算成英尺为4.16英尺,设置左侧硬路肩宽度至少为2.5 m,换算成英尺为8.3英尺,则计算出来的CMF值,以及将条件改变前的CMF值作为基准值进行归一化处理后的CMF值如表3所示。
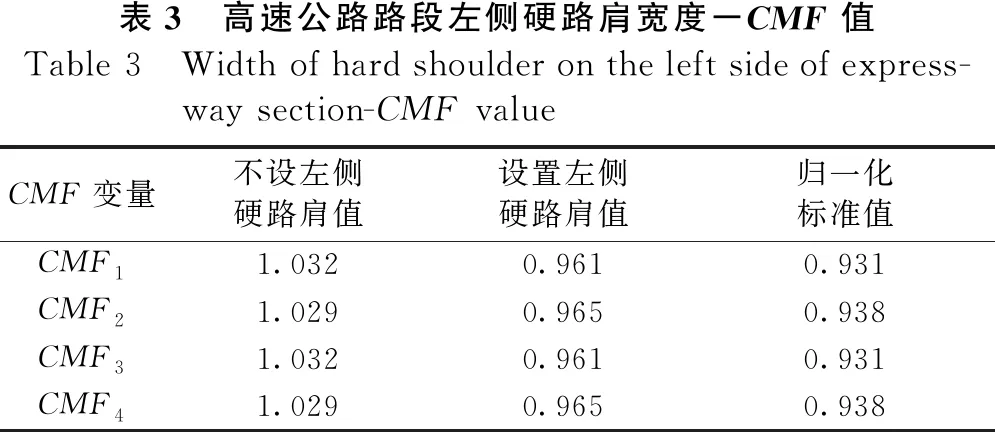
表3 高速公路路段左侧硬路肩宽度-CMF值Table 3 Width of hard shoulder on the left side of express-way section-CMF valueCMF变量不设左侧硬路肩值设置左侧硬路肩值归一化标准值CMF11.0320.9610.931CMF21.0290.9650.938CMF31.0320.9610.931CMF41.0290.9650.938
从表3中可以看出,增设最小宽度为2.5 m的左侧硬路肩后,与左侧硬路肩相关的有人员伤亡的多车事故/单车事故发生频率为0.931,仅财产损失的多车事故/单车事故发生频率为0.938,分别减少了0.069和0.062。
4.2.3事故预测回归模型的建立
本文基于Box-Cox变换,分别以每公里多车/单车事故率为因变量,建立相应的事故预测模型。数据来源为广深高速2010—2020共10 a统计的25个互通间相关因变量与自变量数据,统计周期为半年,共500组数据,取前6 a数据构建模型,后4 a数据验证模型。
选择逐步回归法筛选自变量,取显著性水平为0.05,运用stata14.0统计分析软件,通过最大似然估计,运用Box-Cox变换得到每km多车/单车事故率拟合模型,记经过Box-Cox变换后的因变量为y′i,各自变量为x′i。每公里多车/单车事故率模型分析结果如表4所示。
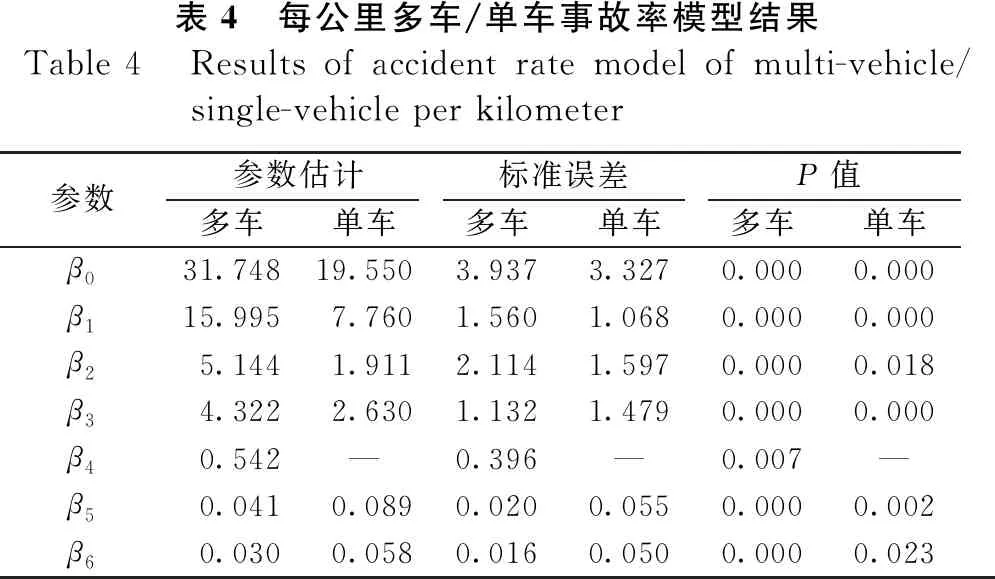
表4 每公里多车/单车事故率模型结果Table 4 Results of accident rate model of multi-vehicle/single-vehicle per kilometer参数参数估计标准误差P值多车单车多车单车多车单车β031.74819.5503.9373.3270.0000.000β115.9957.7601.5601.0680.0000.000β25.1441.9112.1141.5970.0000.018β34.3222.6301.1321.4790.0000.000β40.542—0.396—0.007—β50.0410.0890.0200.0550.0000.002β60.0300.0580.0160.0500.0000.023
每1 km多车事故率模型结果为:
y′1=31.748+15.995x′1+5.144x′2+4.322x′3+
0.542x′4+0.041x′5+0.030x′6
其中,λ为0.710,P值为0.000,远小于0.05;R2为0.938,调整R2为0.935,说明模型中各因素能解释因变量的程度大于93%,模型的拟合结果较好。
每1 km单车事故率模型结果为:
y′2=19.550+7.760x′1+1.911x′2+2.630x′3+
0.089x′5+0.058x′6
其中,λ为0.450;P值为0.000,远小于0.05,R2为0.817,调整R2为0.810,说明模型中各因素能解释因变量的程度大于80%,模型的拟合结果较好。
采用式(15)传统广义线性模型进行回归,并用后4 a事故数据作为测试验证。平均绝对百分比误差(MAPE)能准确反映预测结果偏离实际值的平均程度,是衡量预测精度的重要指标。
(22)
式中:yi为实际事故数;y′i为预测事故数。
预测结果如图3所示,Box-Cox变换后MAPE为15.95%,较传统线形模型21.29%降低了5.34%,提高了事故预测精度,能够应用于左侧硬路肩设置判断算法。
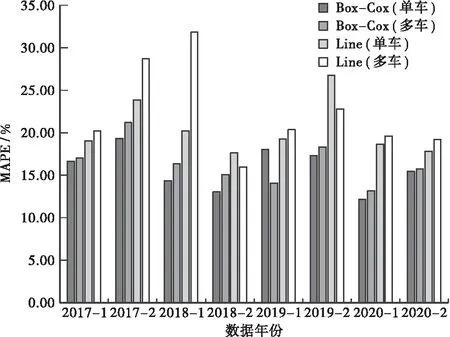
图3 预测误差比较
4.3 结果分析
2025年为广深高速公路改扩建完成年,20 a为使用年限。采用《广深高速公路改扩建可行性报告》中2045年的预测数据,代入算法后得到各路段左侧硬路肩设置系数指标值如图4所示。
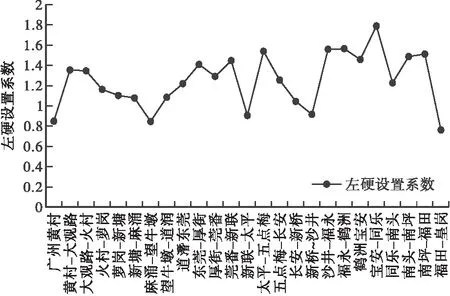
图4 互通左侧硬路肩设置系数指标值
根据设置指标值得出:广深高速广州-黄村、麻涌-望牛墩、新联-太平、新桥-沙井、福田-皇岗5个互通增设左侧硬路肩的K值小于1,可不设置左侧硬路肩,可以适当更改路基形式;其余互通增设左侧硬路肩的K值大于1,故建议设置左侧硬路肩。
设置左侧硬路肩完成后根据以下几个方案进行评价:①所有互通不设左硬;②所有互通均设置左硬;③推荐方案部分设置左硬。方案评价如图5所示,发现采用推荐方案部分设置左侧硬路肩内部收益率最高且大于折现率,相较不设置方案提升52%,较全部设置方案提升20%,不仅节约了部分成本而且实现了左侧硬路肩设置效益最大化。
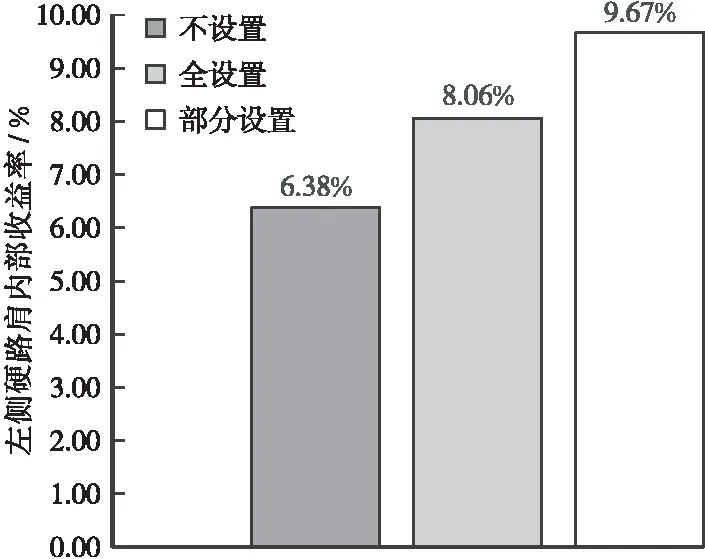
图5 左侧硬路肩设置方案内部收益率
5 结论
a.针对国内改扩建整体式多车道高速公路是否设置左侧硬路肩存在的争议,以成本-效益法为基础提供了一套判别算法,该方法分析了设置左侧硬路肩的成本与带来的效益,建立了左硬设置指标。
b.运用Box-Cox变换对非正态数据进行拟合,建立了事故预测模型,得到平均交织程度、货车比例、路段v/c比、平面均衡指标、纵断面相对势能与因变量显著相关,且模型预测误差相较传统广义线性模型降低了5.34%;继而通过分析左侧硬路肩主要作用,构建CMF值得到左硬可减少的相关事故数。
c.左侧硬路肩设置判别算法实现了高速公路改扩建设置左侧硬路肩效益最大化,内部收益率较不设置方案提升52%,较全部设置方案提升20%。
如今高速公路改扩建成为一个大趋势,未来整体式超多车道高速公路的左侧硬路肩是否设置的争论还会持续,平息争论还需要从更多的角度去论证。由于可搜集到的数据有限,本文中关于设置左侧硬路肩的成本只是平均估算,每个路段可能与真实相差很大,另外效益测算只考虑了主要部分,后期数据的完善可能会影响结论,但不影响本文方法的应用价值。

