表贴式永磁同步电机多步预测控制简化算法

李耀华， 苏锦仕， 秦辉， 赵承辉， 秦玉贵， 周逸凡

(长安大学 汽车学院，陕西 西安 710064)

0 引 言

永磁同步电机(permanent magnet synchronous machine,PMSM)具有体积和质量小、机电能量转换效率高等优点，被广泛应用于电动汽车、轨道交通和风力发电等领域[1]。有限集模型预测转矩控制(finite control set-model predictive torque control，FCS-MPTC)直接利用变换器离散特性和开关状态有限的特点，将由逆变器开关状态直接确定的基本电压矢量作为控制量，通过枚举所有控制量求得最优解，近年来成为永磁同步电机研究的热点[2-7]，目前研究主要为单步预测控制[8-10]。

近年来，多步预测控制逐步受到关注[11-12]。如果仍采用单步预测使用的枚举搜索法(exhaustive search algorithm，ESA)求多步预测控制成本函数的最优解，则计算量会随着预测步数的增加而呈指数增长，无法在极短采样时间内完成运算。因此要将多步预测控制应用于电机控制系统，必须研究适当的简化方法。文献[13]建立了一种转矩和磁链解耦的简化多步预测控制模型，使用查表法和加法运算进行多步预测，与含有平方根和三角函数的传统预测控制模型相比，运算量较小，并利用每一步预测的成本函数限制控制量的选择范围，避免了对所有控制量的枚举，在较短的采样周期内实现多步预测控制。文献[14-15]提出一种两步预测的简化算法，在单个控制周期内仅考虑最优和次优开关状态，确保在两个控制周期内所选开关状态最优。文献[16-17]将多步预测控制的优化问题转换为整数最小二乘问题，使用球面解码算法求得最优解。文献[18]采用滑动时域策略，将预测时域分成两部分，第一部分离当前时刻较近，使用较小的采样时间Ts进行高分辨率采样，第二部分离当前时刻较远，以Ts的倍数作为采样时间进行粗略采样，实现了较多步数的预测控制，而且降低了运算量。文献[19]采用分支定界法，当目标函数值达到预先设定的上下限，或者计算步骤数超过设定阈值，则停止多步预测控制优化过程以减少平均计算量。

本文建立两电平三相逆变器驱动的表贴式永磁同步电机(surface PMSM, SPMSM)多步FCS-MPTC模型，分析传统MPTC算法(traditional-MPTC, T-MPTC)的运算量，然后在文献[21]“精简电压矢量集合”法(simplified set-MPTC, S-MPTC)基础上，提出一种多步MPTC新型简化算法—“电压矢量保持”MPTC算法(voltage preserving-MPTC，P-MPTC)，该算法能在一定条件下避免遍历备选电压矢量集中的所有电压矢量，从而进一步减少运算量。定义性能和运算量评价指标后，对所提出算法的控制性能和运算量进行评估，与T-MPTC、S-MPTC算法进行对比分析，验证所提出算法的有效性。

1 SPMSM未简化多步MPTC算法

1.1 表贴式永磁同步电机数学模型

忽略定子电阻压降，表贴式永磁同步电机在定子x-y坐标系下磁链和转矩方程分别为：

(1)

(2)

式中：us、is分别为定子电压矢量、定子电流矢量；ψs、ψf、Te分别为定子磁链矢量、永磁体磁链矢量、电机转矩矢量；Rs为定子电阻；p为电机极对数；Ld为d轴电感；δ为转矩角。

1.2 多步MPTC模型

控制量为两电平三相逆变器的7个基本电压矢量，即

Vs∈{V0,V1,V2,V3,V4,V5,V6}。

(3)

零电压矢量可以由两个开关状态(000和111)生成，以开关次数最小原则来选择具体开关状态。

由于采样周期极短，忽略电机转子旋转运动和定子电阻压降，定子磁链x-y坐标系下，k时刻施加电压矢量Vs后，k+1时刻的定子磁链幅值为：

(4)

(5)

忽略一个采样周期内转子旋转运动，近似认为定子磁链角位置变化量与转矩角变量相等，则k+1时刻的定子磁链角位置、k+1时刻的转矩角分别为：

(6)

(7)

式中：θs(k)为k时刻的定子磁链角位置；δ(k)为k时刻的转矩角。

k+1时刻的电机转矩值为

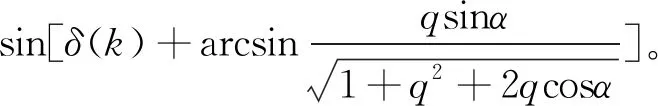
(8)

式(4)～式(8)称为SPMSM预测转矩控制基本模型，多步MPTC每一步预测计算都要使用这个基本模型，下文简称为“基本模型”。模型预测转矩控制“基本模型”计算流程如图1所示。

图1 MPTC“基本模型”

1.3 成本函数计算和参考值确定

N(N为正整数)步预测中第i步预测的成本函数为

(9)

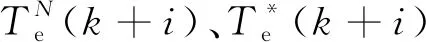
将每一步的成本函数gi累加起来，得到一个总的成本函数，即

(10)

当采样频率较高时，可近似以k时刻的参考值作为k+i时刻的参考值，即

(11)

多步模型预测控制通常采用滚动时域控制策略(receding horizon control，RHC)确定逆变器的开关状态。在k时刻选出使得总成本函数g最小的控制变量序列作为k时刻最优控制变量序列，在k+1时刻仅将最优控制变量序列的第一个分量作用于电机控制系统，并在k+1时刻根据最新的电机状态观测值重新预测，得到对应于k+2时刻的最优控制变量序列，即在每一个采样周期都重复进行开关状态的优化过程，在下一个周期仅施加最优序列的第一个控制量，不断向控制回路提供反馈。

1.4 传统多步MPTC算法流程与运算量

在k时刻基于枚举算法的传统N步(N为正整数)MPTC(T-MPTC)的步骤为：

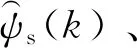
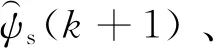
3)以此类推，将(k+i-1)步的预测值和7个备选电压矢量带入至“基本模型”，可到k+i步的预测值。遍历结束后，最终得到7N个控制序列。

4)依次将每一个控制序列对应的转矩、定子磁链幅值预测值带入成本函数式(10)，选出使成本函数值最小的控制序列作为最优控制序列。至此完成k时刻的N步预测运算。

5)根据滚动时域控制策略，仅将步骤4)中得到的最优控制序列的第一个控制量作用于k+1时刻，并在k+1时刻根据电机最新的状态，开始k+1时刻的N步预测运算，重复步骤1)～5)。

由此可得，N步MPTC控制系统的结构如图2所示。

图2 N步MPTC系统的结构图

对于M个备选控制量的N步T-MPTC而言，在一个采样周期内需要调用“基本模型”的次数为

(12)

得到7N个电压控制序列。

随着备选控制量个数M、预测步数N的增大，运算量会急剧增加。T-MPTC算法中，备选控制量个数M= 7，随着预测步数N的增加，运算量呈指数形式上升，电机控制系统难以在极短采样时间内完成运算，因此需要研究简化算法。

2 SPMSM多步MPC简化算法

文献[21]对7个备选电压矢量的利用率进行统计，剔除利用率较低的电压矢量，得到精简电压矢量集合，减小了MPTC计算量。为方便表述，将文献[21]中的简化方法称为“精简电压矢量集合”法。文献[21]中的一个精简电压矢量集合如表1所示，其中：φ、τ分别为磁链和转矩滞环控制信号；w为定子磁链所在扇区。函数f(x)表示电压矢量序号，mod表示取余运算，则有

表1 精简电压矢量集合

f(x)=mod(x-1,6)+1,x=1,2,3,4,5,6。

(13)

由表1可知，精简电压矢量集合中的元素随着定子磁链扇区、转矩和磁链控制信号φ、τ变化，备选电压矢量个数从7个精简到3个。使用精简电压矢量集合可以缩小电压矢量的选择范围，但每一步预测中仍然需要遍历每一个备选电压矢量，运算量仍然较大。

在文献[21]的基础上，本文提出一种采用“电压矢量保持”策略的多步MPTC简化算法，在满足一定规则时，k+p步预测可以直接采用(k+p-1)步选择的电压矢量，而无需遍历所有备选电压矢量，进一步简化运算。P-MPTC控制策略如下：

1)k+1步：使用精简集合中备选的3个电压矢量进行预测。

2)k+p步：p为整数且2≤p≤N，设k+p步可选择的电压矢量集合为Φ，(k+p-1)步选择的电压矢量为Vj。若Vj∈Φ，则(k+p)步直接选择电压矢量Vj，不再需要遍历集合Φ中的其他电压矢量；否则将遍历集合Φ中所有3个电压矢量，并选出使(k+p)步的成本函数最小的电压矢量作为(k+p)步最终选择的电压矢量。

传统T-MPTC每一步预测都需要枚举7个控制量，S-MPTC算法中，每一步预测都需要枚举3个控制量，P-MPTC算法每一步预测最多需要枚举3个控制量，特定情况下，每一步只需要进行一次预测计算，从而进一步简化预测计算量。

3 仿真验证

仿真对比T-MPTC、S-MPTC、P-MPTC 3种控制策略下N步MPTC的实际控制效果和运算量，预测步数N分别取1～6。

3.1 仿真条件和评价指标

仿真时长为2 s，采样周期Ts为50 μs。直流母线电压Udc为312 V。参考转速初始值为500 r/min，0.5 s时阶跃至750 r/min，1.5 s时阶跃至500 r/min。负载转矩初始为10 N·m，1 s时阶跃至20 N·m。参考定子磁链幅值为0.3 Wb。转矩环PI参数Kp=10，KI=5×10-5，转矩滞环宽度为0.02 N·m。定子磁链幅值滞环宽度为0.002 Wb。仿真用SPMSM参数如下：定子电阻为0.2 Ω；d轴和q轴电感均为0.008 5 H；转子磁链0.175 Wb；电机极对数为4；转动惯量0.089 kg·m2；粘滞阻尼0.005 N·m·s。

定义电机控制效果评价指标为转矩脉动均方根误差TRMSE、转速均方根误差ωRMSE和定子磁链幅值均方根误差ψRMSE分别如下：

(14)

(15)

(16)

定义运算量的评价指标为绝对运算次数Tcal_all、相对运算量λ、运算量增长率η。

绝对运算次数Ttotal表示整个仿真时长内“基本模型”被调用的次数，对于T-MPTC和S-MPTC，可以直接用下式计算运算次数：

Ttotal=nTone_step。

(17)

式中Tone_step为一个采样周期内的“基本模型”被调用的次数，可由式(12)计算，n为采样周期个数。由于P-MPTC的每一步运算次数并不固定，Ttotal不能直接用公式计算，需要预测过程中实时统计。

由于各个策略的实际运算次数可能相差较大，不便于直接观察比较，进一步采用相对运算量和运算量增长率评价指标。

相对运算量λ：在特定预测步数N时，一个控制策略的绝对运算次数与T-MPTC的绝对运算次数之比，可以反映同一预测步数时，不同控制策略间的运算量差异。

运算量增长率η：同一种控制策略N步MPTC与N-1步MPTC的绝对运算次数之比，可以反映同一种控制策略的运算量与预测步数N的关系。

3.2 控制性能对比

图3～图5给出了T-MPTC、S-MPTC、P-MPTC 3种控制策略在不同预测步数N时的性能评价指标变化情况。由图可知：与T-MPTC算法相比，S-MPTC算法和P-MPTC算法的转速均方根误差ωRMSE、转矩均方根误差TRMSE、定子磁链幅值均方根误差ψRMSE都有小幅上升，表明两种简化策略均牺牲了部分磁链和转矩控制性能。

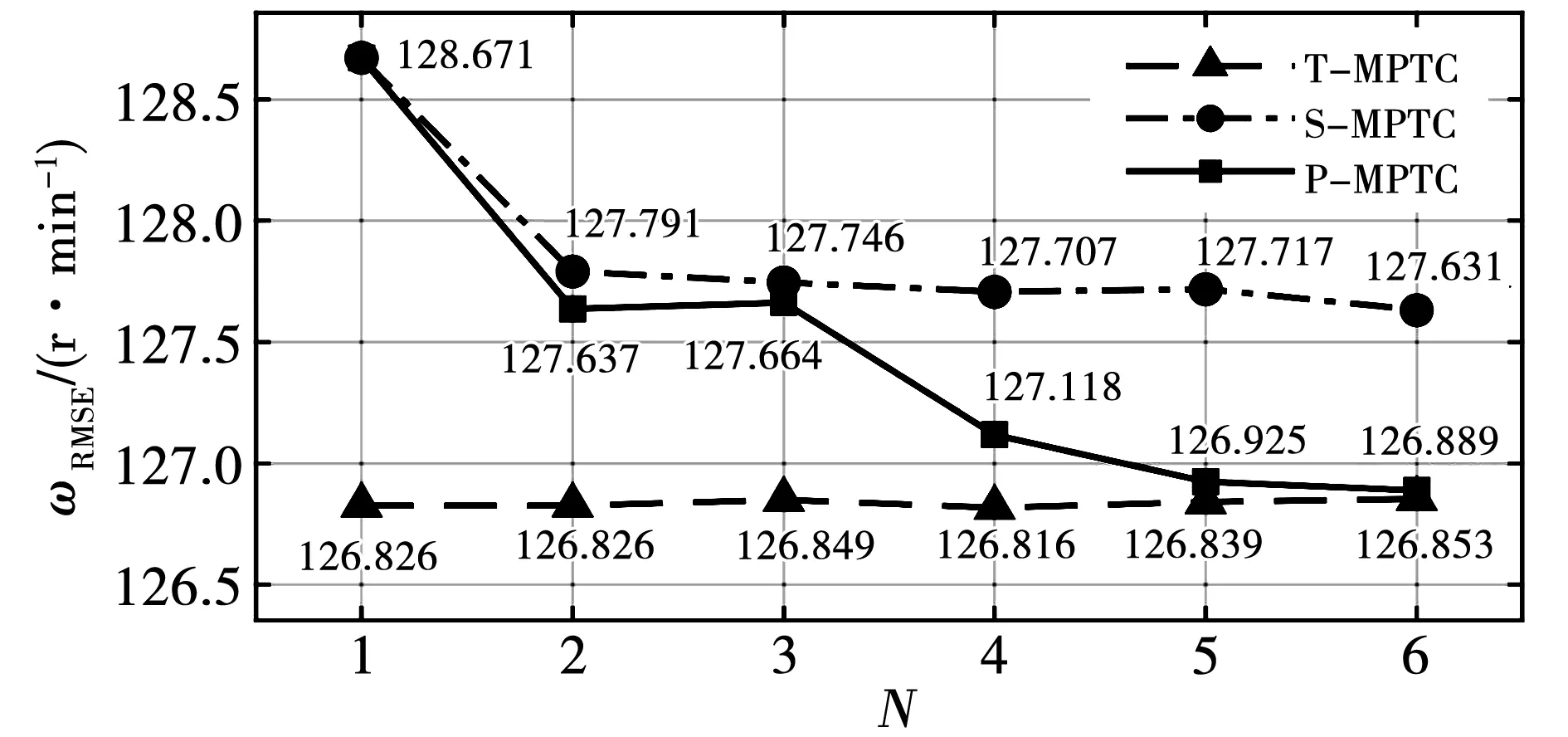
图3 电机转速均方根误差

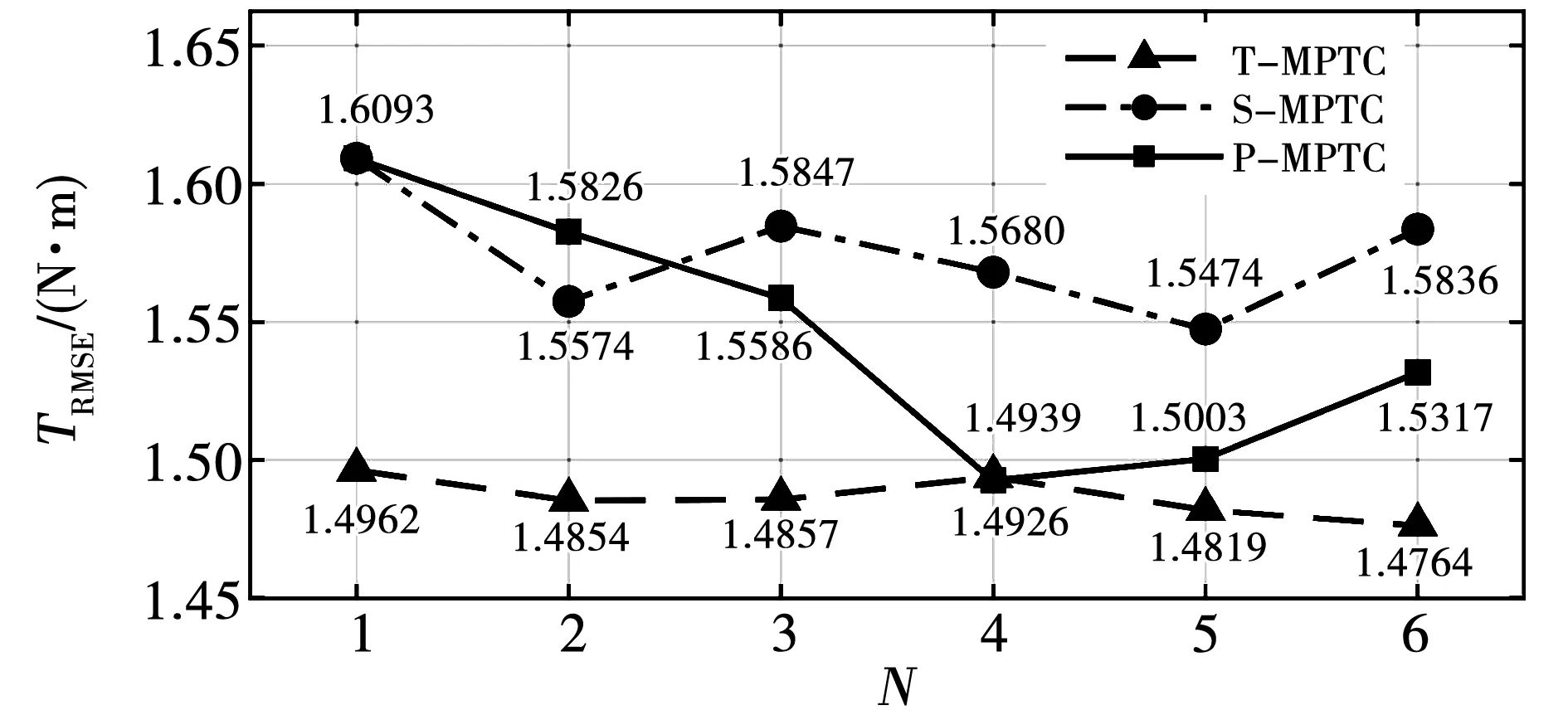
图4 电机转矩均方根误差

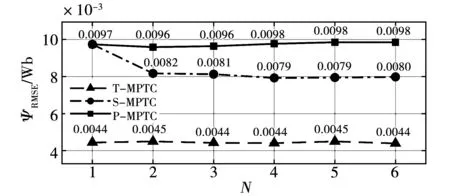
图5 定子磁链幅值均方根误差

图6为预测步数N=5时，3种控制策略对应的电机转矩、定子磁链幅值、转速、A相定子电流的波形图。图6表明：3种控制策略下，电机系统运行良好，控制性能基本相当。与其他两种算法相比，P-MPTC算法的定子磁链幅值脉动略大，但是电机转速值、转矩值仍能较快跟踪相应参考值的变化，动态响应性能基本不变。

图6 N=5时，3种控制策略的控制性能

3.3 运算量对比

图7、图8分别表示不同控制策略的运算量增长率、相对运算量与预测步数N的关系。可见，S-MPTC和P-MPTC算法均能明显减小运算量，且P-MPTC算法的运算量更小，表明在精简集合的基础上施加“电压矢量保持”策略，可以进一步减少运算量。例如，当N=6，S-MPTC算法相对运算量λ约为0.8%，而P-MPTC算法的相对运算量λ约为0.02%，即仅相当于T-MPTC算法运算量的0.02%，从而极大简化了多步MPTC运算。

图7 相对运算量变化曲线

图8 不同控制策略的运算量增长率

随着预测步数N的增加，S-MPTC、P-MPTC算法的运算量增长率η、相对运算量λ都在减小，表明预测步数N越大，简化效果越明显。在预测步数N较小时(N=1, 2, 3)，η、λ变化较为迅速，而预测步数较大时(N=4,5,6)，运算量增长率η曲线、相对运算量λ曲线都在逐渐变得平缓，表明简化效果逐渐趋于平稳。

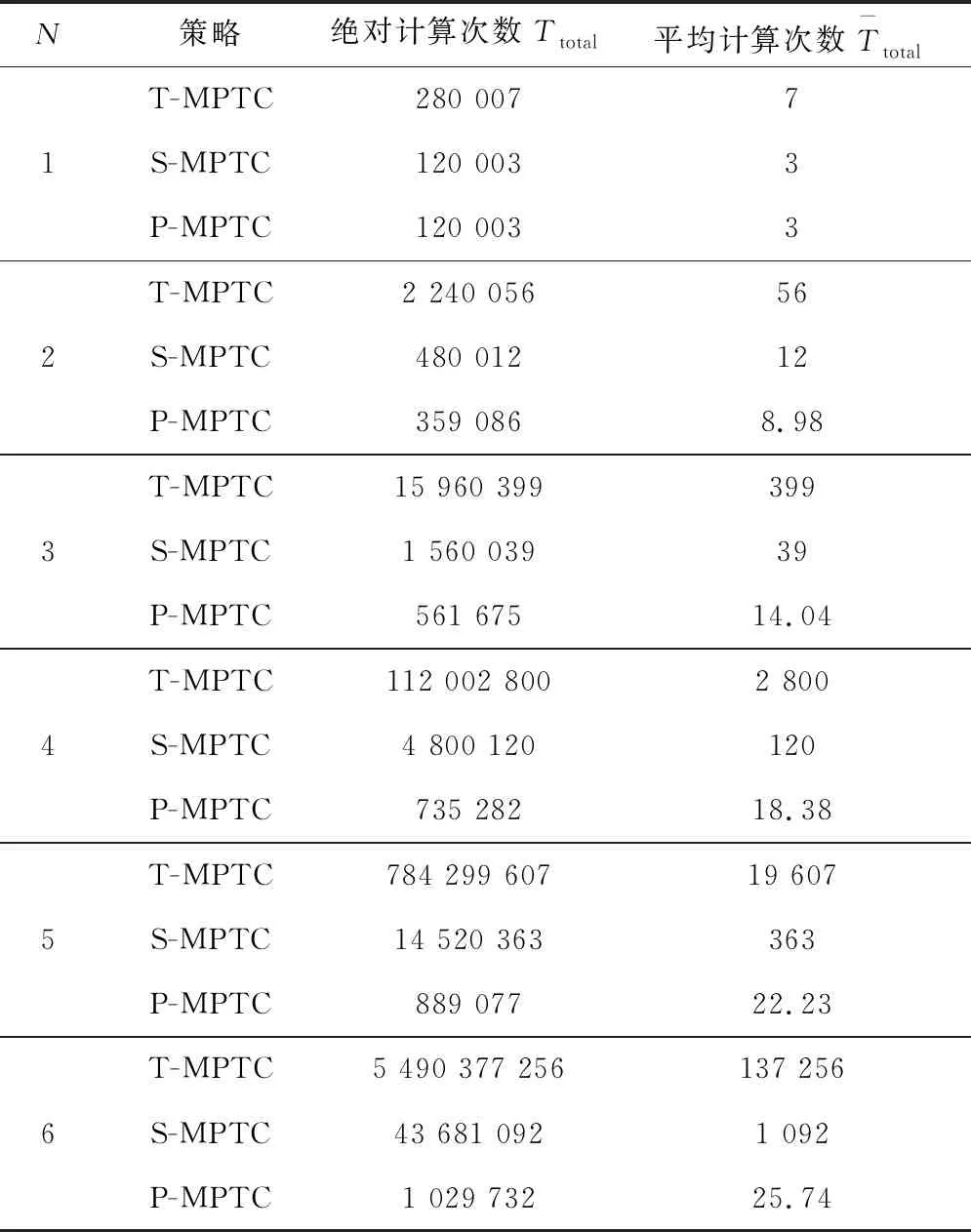
表2 仿真过程的绝对计算次数与平均计算次数

由表可知，S-MPTC和P-MPTC算法极大降低了平均计算次数。以六步预测为例，T-MPTC平均计算次数为137 256次，S-MPTC平均计算次数为1 092次，而P-MPTC平均计算次数仅为25.74次。

综合可知，在精简集合的基础上施加“电压矢量保持”策略的简化算法，可在保证电机转矩、磁链、转速控制性能基本不变的情况下，显著减少多步MPTC的运算量。

4 硬件平台验证

基于STM32H743单片机平台对以上3种控制策略进行单步测试，测试不同算法的执行时间。

单步测试电机控制系统参数与上文仿真系统相同。单步测试初始值如下：定子磁链幅值为0.313 5 Wb；定子磁链角位置为 36.027 9°；参考转矩值为10.730 6 N·m；转矩值为9.151 2 N·m；转矩角为14.116 0°；定子磁链参考值为0.3 Wb；电机转速为498.927 3 r/min。

为了分析不同算法的运行时间，将算法程序运行时间分为以下3部分：

1)预测计算时间(t1)，用于计算k+i步的预测值；

2)判断过程时间(t2)，简化策略额外增加的时间，用于确定转矩、磁链滞环控制信号，确定备选电压矢量等；

3)评价过程时间(t3)，用于计算成本函数，选出最优电压矢量序列。

预测步数N取1～6。对每种控制策略的不同预测步数N，在单片机重复执行10次，并取执行时间的平均值作为算法执行时间。3种MPTC算法的硬件执行时间和结果如表3所示，表中的总时间为预测计算时间、评价过程时间、判断过程时间之和，执行次数为本次单步测试中“基本模型”被调用的次数。

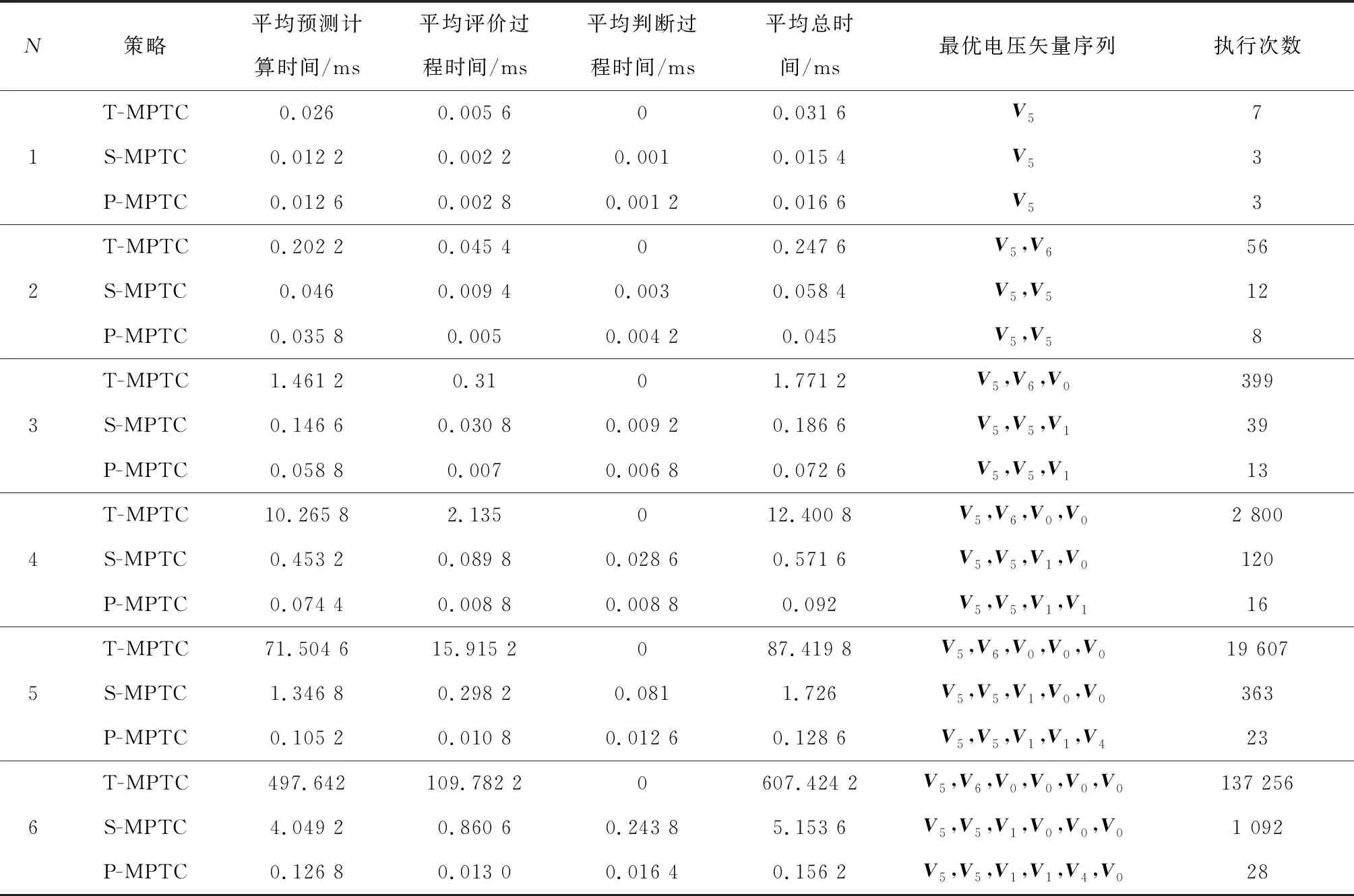
表3 3种MPTC算法的硬件执行时间和计算结果

表3同样表明S-MPTC和P-MPTC两种简化算法均能较大幅度降低预测计算和评价过程所需时间。虽然简化算法需要额外增加判断过程时间，但其远小于预测计算和评价过程时间的减少量。因此，简化算法总执行时间远小于T-MPTC执行时间。

以六步预测为例，与T-MPTC相比，S-MPTC和P-MPTC虽然增加一个判断过程，增加0.243 8和0.016 4 ms计算耗时，但减小“基本模型”调用次数，将执行次数从137 256次分别减少到1 092次和28次，从而减小预测计算和评价过程时间。与T-MPTC相比，预测计算用时由497.642 ms减小到4.049 2和0.123 8 ms，评价过程用时由109.782 2 ms减小到0.860 6和0.013 0 ms，执行总时间由607.424 2 ms减小到5.153 6和0.156 2 ms。由此可见，S-MPTC和P-MPTC极大减小计算运算量，提高系统实时性能。

对于单步测验验证，将相对运算量λ定义为对于每一个预测步数N，各控制策略执行总时间与T-MPTC算法执行总时间之比。将运算量增长率η定义为同一种控制策略的N步预测与N-1步预测的执行总时间之比。仿真和硬件执行过程的相对运算量λ、运算量增长率η的数据如表4所示。

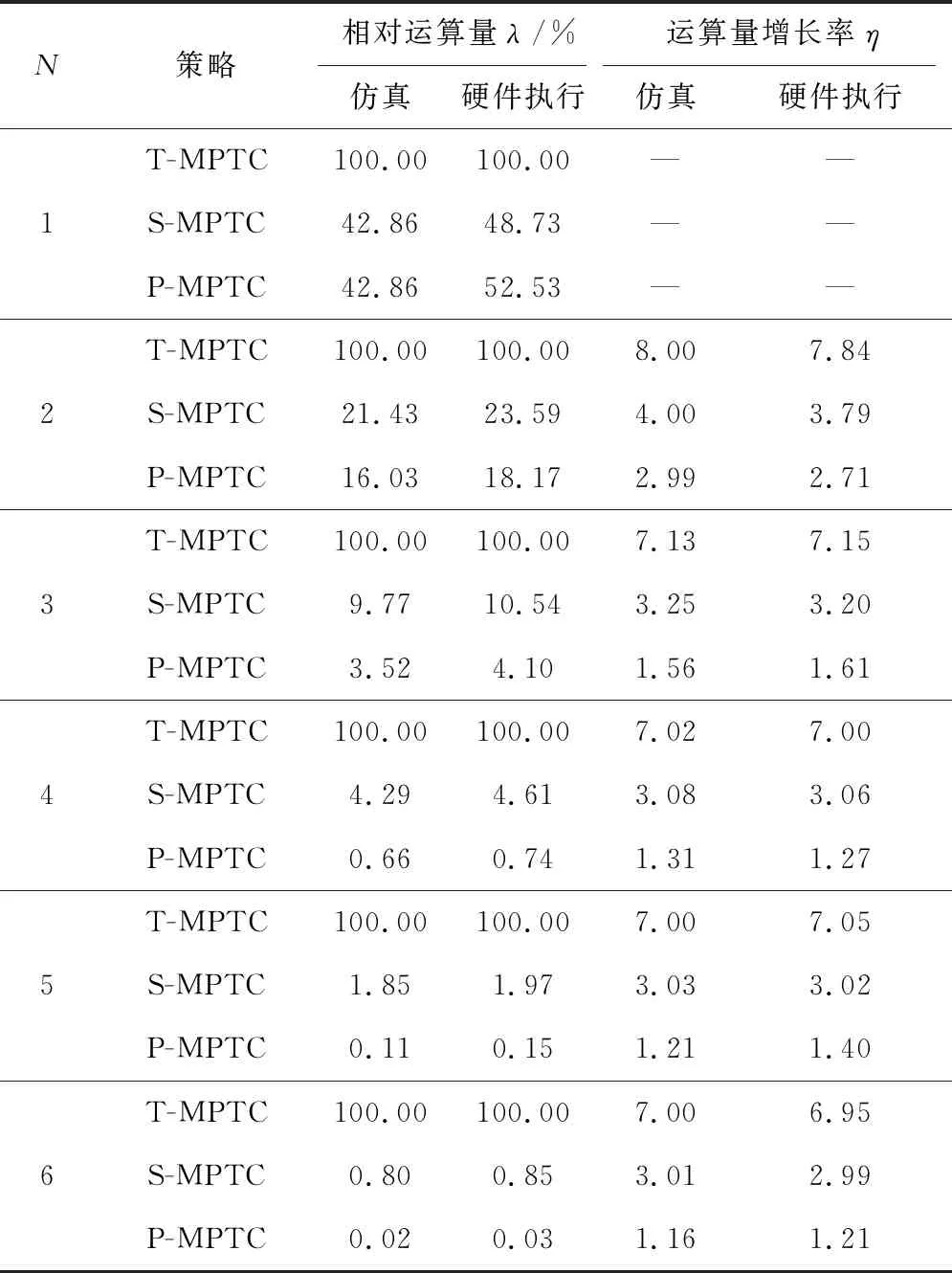
表4 仿真过程和硬件执行运算量指标对比

表4表明，仿真和硬件执行过程的相对运算量和运算量增长率结果基本吻合，进一步验证了S-MPTC、P-MPTC算法均能明显减小运算量，且P-MPTC算法简化效果更显著的结论。

5 结 论

本文建立了表贴式永磁同步电机的多步FCS-MPTC模型，并在“精简电压矢量集合”法的基础上，提出一种新型简化算法，定义了“相对运算量”、“运算量增长率”两个运算量评价指标。所提出的算法采用“电压矢量保持”策略，一方面，将备选控制量数量从7个减少到3个，缩小每一步预测中控制量选择范围；另一方面，在满足特定规则时，某一步预测可以直接采用上一步预测选择的电压矢量，避免遍历备选电压矢量集中的所有电压矢量，与“精简电压矢量集合”法相比，进一步降低了多步预测的运算量和复杂度。仿真结果和单片机平台执行结果验证了该算法的有效性，所提出的算法能保证电机转矩、转速、磁链控制性能、动态响应性能基本不变的前提下，极大减少多步模型预测运算量。