交流电机模型预测控制综述
王治国, 郑泽东, 李永东, 孙嘉伟, 周培毅
(1.陆军装甲兵学院 兵器与控制系,北京 100072; 2.清华大学 电力系统及大型发电设备安全控制和仿真国家重点实验室,北京 100084)
0 引 言
近年来,随着先进控制理论和技术不断发展,线性控制、非线性控制、智能控制以及预测控制等先进控制方法在交流电机控制中得到了广泛应用,大幅度提高了电机的控制性能。相对于其他控制方法,预测控制具有概念直观易于理解;能够提高系统响应速度;能够处理含有约束条件的多变量非线性控制问题;能够实现多目标优化;直接将变换器的开关特性考虑在模型中,容易实现直接控制等优点,从而成为交流电机控制研究的热点和主要的发展方向。
预测控制(predictive control,PC)是指具有预测被控对象未来变化的功能,同时将预测结果用于控制,以获得更好性能的控制方法[1]。这种方法不是建立在某种特定控制理论上的特殊控制方法,而是在启发式控制方法的基础上,从不同领域中发展起来的一类控制方法[2]。预测控制的突出特点是与计算机紧密结合,主要特征是使用模型来预测被控变量的未来值,并将预测值用于优化。
预测控制在工业领域和电机控制领域中的含义存在一定差别。工业领域中,很多学者都将模型预测控制(model predictive control,MPC)作为多种预测控制方法(例如:模型算法控制、动态矩阵控制等)的通用名称[2-5]。电机控制领域中,预测控制包含无差拍控制、基于滞环的预测控制以及基于轨迹的预测控制等,而MPC则特指预测控制中的一类具体方法[6]。
过去三十年间,MPC在交流电机控制领域中取得了较大发展,在交流电机电流控制、磁链及转矩控制、速度控制以及位置控制中获得了广泛关注和研究。尽管进展明显,仍然存在一些需要进一步研究和解决的问题,例如:如何进一步提高控制的静态特性,如何提高控制的稳定性和参数鲁棒性,如何设计MPC的参数等。
文献[7]是电力传动领域中预测控制较早的综述文献。该文献讨论了预测控制的特点以及基于滞环和基于轨迹的预测控制方法;文献[6]讨论了电力电子领域中预测控制的分类和特点,给出了MPC的分类、原理以及应用;文献[8-9]全面的综述了有限控制集模型预测控制(finite control set MPC,FCS-MPC)在电力电子领域中的应用及关键问题,并对比了FCS-MPC与线性控制器的特性;文献[10]针对FCS-MPC在感应电机磁链和转矩控制中的应用,综述了减小控制复杂度、设计权重系数以及提高稳态特性等方面的现状和发展;文献[11]综述了电力电子和电力传动领域中MPC的分类及应用,讨论了评价函数、优化方法等MPC应用中的关键问题。
本文针对交流电机控制,以预测和优化方法的区别为标准,给出了MPC的详细分类,并以此为基础讨论MPC的发展和现状、应用中存在的主要问题以及发展趋势。
1 模型预测控制原理
模型预测控制是通过被控对象的模型来预测被控变量未来的变化趋势,并通过优化算法得到控制变量的一类控制方法。这类控制方法的突出特点是与计算机密切结合,采用离散形式的模型构成数字控制系统;其主要特征是在每个控制周期都使用模型来预测被控变量的未来值,并在预测的基础上实现对控制变量的滚动优化。
1.1 模型预测
MPC对模型形式没有严格的要求,只要模型能够预测被控变量未来的变化即可。因此,传递函数、动态矩阵以及状态空间等形式的模型都可以用于MPC。交流电机有成熟的参数模型,且可以方便地表示为一阶微分方程组的形式,因此,常用状态空间模型来实现交流电机的模型预测:
(1)
式中:x(k)=[x1(k)…xn(k)]T∈X⊂Rn为状态变量;u(k)=[u1(k)…um(k)]T∈U⊂Rm为输入变量;d(k)=[d1(k)…dg(k)]T∈D⊂Rg为扰动量;y(k)=[y1(k)…yp(k)]T∈Y⊂Rp为输出变量;Ad、Bd、Ed以及Cd分别为系统矩阵、输入矩阵、扰动输入矩阵以及输出矩阵。
以k为初始时刻,以x(k)为系统变量初始值,由式(1)可得被控变量在k+l时刻的模型预测值为
(2)
针对某个控制变量序列
U(k)={u(k),u(k+1),…,u(k+Nc-1)},
(3)
利用式(2)进行迭代计算,可以得到与控制变量对应的预测序列
Y(k)={y(k+1|k),y(k+2|k),…,
y(k+Np|k)}。
(4)
式中:Nc为控制域长度;当k>Nc时,u(k)=0;Np为预测域长度,通常Np≥Nc。
1.2 评价函数
MPC通常利用评价函数实现对控制变量的优化。MPC对评价函数的形式没有严格的要求。对于连续控制集模型预测控制,可以采用1-范数、2-范数或∞-范数等形式的评价函数;对于采用枚举法优化的有限控制集模型预测控制,评价函数的形式可以更加灵活,与被控变量有非负数量关系的性能指标都可以加入评价函数进行优化[9]。2-范数形式的评价函数为

(5)
式中:l=1,2,…,Np;h=0,1,2,…,Nc;Ql为k+l时刻对输出变量误差的权重系数矩阵;Rh为k+h时刻对控制变量的权重系数矩阵。
求解使评价函数J取最小值的有约束优化问题可以得到k时刻的最优控制序列为
U*(k)={u*(k),u*(k+1),…,
u*(k+Nc-1)}。
(6)
1.3 滚动优化
尽管式(6)给出了k时刻控制域Nc内所有控制变量的最优解,但应用中只取最优控制序列中与k时刻对应的元素作为实际使用的控制变量,即
u(k)=u*(k)。
(7)
在k+1控制周期,MPC会重复上面的预测和优化过程,得到新的控制变量最优解序列U*(k+1)以及实际的控制变量u*(k+1)。由上面的分析可以看出,滚动优化不是通过单次优化得到最优解序列,并将其全部用于控制,而是在每个控制周期都进行优化计算,并将最优解序列中与当前控制周期对应的部分作为实际的控制变量。模型预测控制的原理如图1所示。
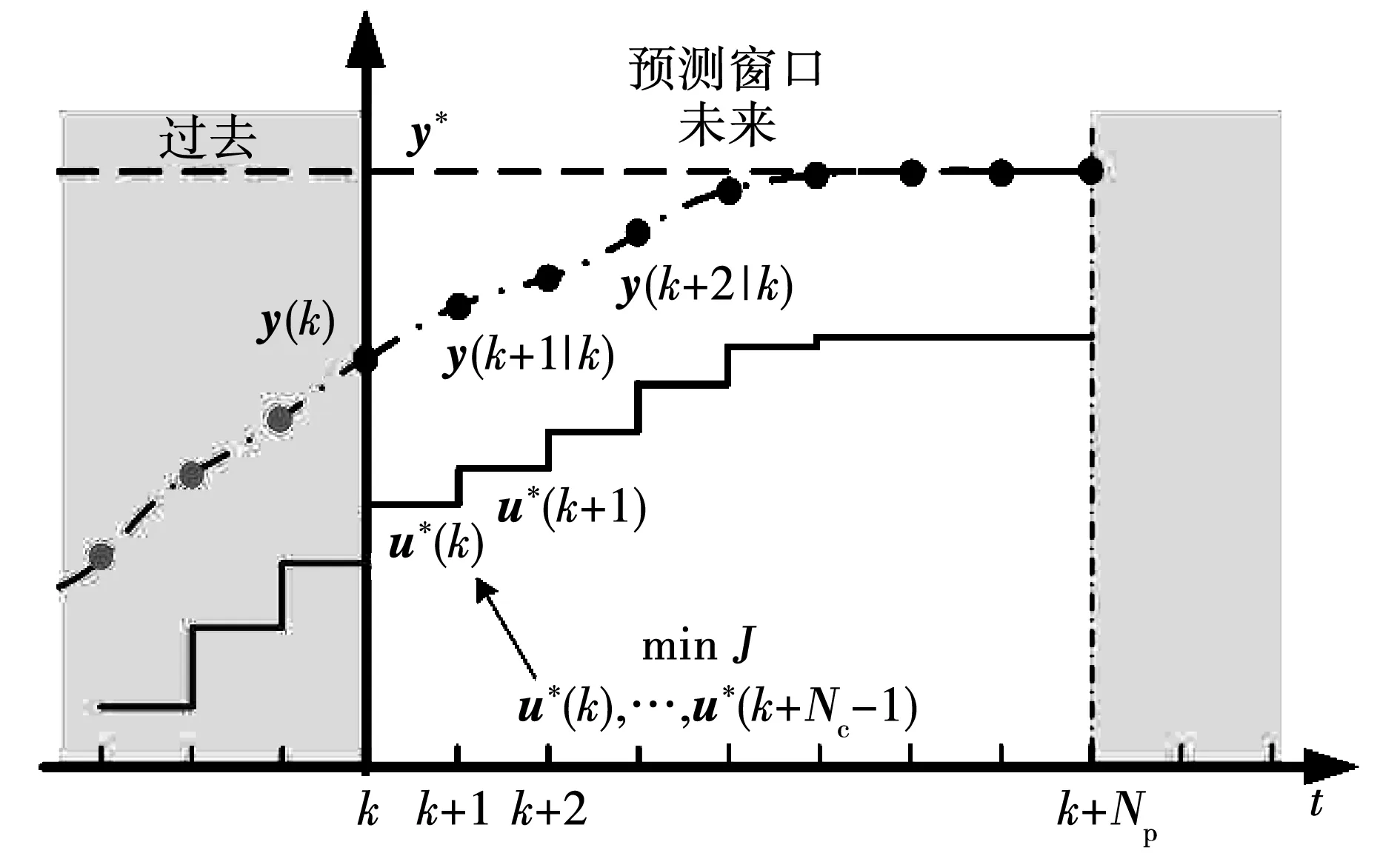
图1 模型预测控制原理
2 交流电机MPC的分类与发展
交流电机控制中,MPC根据控制变量取值范围的特点可以分为连续控制集模型预测控制(continuous control set MPC,CCS-MPC)[12]和FCS-MPC[13]两种基本类型。FCS-MPC可根据控制目标直接确定用于控制功率半导体器件的开关量,不需要使用调制技术,因此又被称为直接模型预测控制(direct MPC,DMPC)[14-15]。CCS-MPC在连续域内计算控制变量的最优解,其输出是连续变量,需要使用调制技术。
2.1 有限控制集模型预测控制
FCS-MPC充分考虑了电力电子变换器采用离散、有限的开关状态实现控制的特点,针对这些开关状态实现预测,然后利用评价函数对这些预测结果进行优化,最终选择使评价函数取值最小的开关状态作为实际的控制变量。FCS-MPC的预测和优化充分结合了电力电子变换器的特点,可以直接得到最优开关状态,去掉了调制环节,简化了控制算法。此外,这类控制方法无需考虑评价函数的解析求解问题,优化目标也更为灵活。因为FCS-MPC具有上述优点,所以在交流电机控制中得到较多的关注和应用。
自C.Attaianese于1993年针对感应电机提出电流预测控制算法[16]开始,FCS-MPC已有近三十年的发展历史。FCS-MPC发展早期主要研究如何利用模型和枚举等基本的预测和优化方法实现对交流电机的控制。随着研究不断深入,FCS-MPC应用中存在的一些基本问题得到了较为系统的研究,例如:滞后补偿、长域预测、参数设计、参数鲁棒性分析和设计等。同时,FCS-MPC的应用范围也得到了进一步扩展,例如:电机存在故障情况下的控制[17]、多目标优化[18]等。
FCS-MPC的分类标准较多,文献[9]以变换器拓扑结构为标准实现了对FCS-MPC的分类(三电平中点嵌位、有源前端整流器、级联H桥逆变器、飞跨电容逆变器、矩阵变换器等),并讨论了其在电力电子领域中的应用。文献[19-20]以应用领域为标准,对FCS-MPC进行了分类和综述(并网变换器、带RL负载的逆变器、带LC滤波器的逆变器、传动逆变器等)。文献[11]则根据优化结果的开关矢量数量将FCS-MPC分为优化开关矢量MPC(optimal switching vector MPC,OSV-MPC)和优化开关序列MPC(optimal switching sequence MPC,OSS-MPC)两种类型。
本文将FCS-MPC预测和优化方法的区别作为分类标准,讨论FCS-MPC在交流电机控制领域的历史发展和现状,具体分类结果如图2所示。
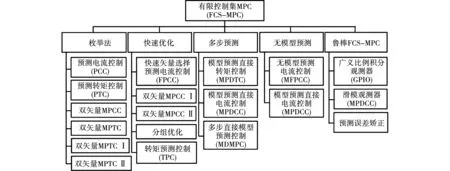
图2 交流电机中FCS-MPC的分类
2.1.1 枚举法预测和优化
枚举法是FCS-MPC最常用的预测和优化方法。2004年,J.Rodríguez针对三相电压型逆变器提出了预测电流控制(predictive current control, PCC)[21],其原理如图3所示。PCC将所有可行的开关矢量代入静止坐标系下的模型,以预测逆变器的输出电流,并通过评价函数找到使电流误差最小的开关矢量作为实际的控制变量。文献[22-25]分别针对三相电机、双三相电机和五相电机,采用一步预测以及枚举法实现了电流控制;文献[26-28]通过枚举法实现了转矩和定子磁链的控制,这类方法又称为预测转矩控制(predictive torque control,PTC)或模型预测转矩控制(model predictive torque control,MPTC)。
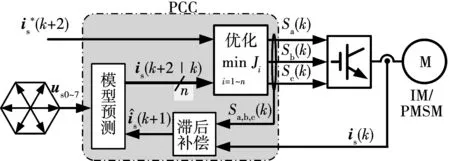
图3 PCC原理
上述传统PCC和MPTC仅采用枚举法对基本开关矢量预测和优化,单个采样周期中仅施加一个固定的开关状态,会导致被控变量存在较大的纹波。为了解决这个问题,张永昌等通过在采样周期中增加零矢量,减小了PCC电流的脉动[29]以及MPTC的磁链和转矩脉动[30],形成了双矢量MPCC[31]和双矢量MPTC[32]。传统的双矢量MPCC和MPTC均首先利用枚举法得到最优矢量,然后针对最优矢量计算占空比。传统双矢量MPCC通常根据“电流误差最小”的优化目标来计算占空比[31,33],文献[34]还提出采用模糊控制确定占空比的方法。传统双矢量MPTC计算占空比的方法较多,例如:使转矩在采样时刻与参考值相等的方法、使平均转矩与参考值相等的方法以及使转矩脉动最小的方法等[35]。
传统双矢量MPTC分开确定最优矢量和占空比的方法导致最终得到的双矢量组合可能并非最优解[33](第一步用枚举法选择最优矢量只能保证整个采样周期都用这个矢量是最优的,但在插入零矢量并得到组合矢量后,就不能保证组合矢量最优)。为了解决这个问题,张永昌等对MPTC进行了改进,先计算各非零开关矢量的占空比,然后将非零矢量及其作用时间作为整体,使用枚举法预测并优化,从而形成双矢量MPTC I算法[30]。将双矢量中的第二矢量放宽到可取任意基本矢量,即形成双矢量MPTC II算法[36]。
枚举法的最大优点是原理简单。这种方法在电路拓扑结构简单时容易实现,但当电路结构复杂(例如:多电平变换器、矩阵变换器等)时,开关状态的数量将急剧增加,导致枚举法的计算量急剧增大,使预测和优化无法实现。此外,随着预测域长度的增加,枚举法的计算量也会迅速增大,从而导致枚举法很难直接应用于长预测域控制。
2.1.2 快速优化
计算量大是制约枚举法应用的主要问题。通过减少枚举次数来降低计算量是解决这个问题的主要思路,从而形成了一些快速优化算法。
自1993年李永东等开始研究转矩预测控制,提出了利用新型电压矢量表计算定子电压矢量和定子磁链矢量间夹角的方法,实现了双矢量快速优化转矩预测控制[37-39]。张永昌等采用类似无差拍控制的思路,提出了基于快速矢量选择的预测电流控制(fast predictive current control,FPCC)方法[40]。FPCC先根据电流参考值计算出理想电压参考矢量,然后利用基本电压矢量与理想参考电压矢量之间的误差实现优化。该方法先通过参考电压矢量所在的扇区选择非零矢量,然后与零矢量对比,经过两次预测就可以完成优化,不需要计算所有基本电压矢量与参考电压矢量间的距离,其原理如图4所示。
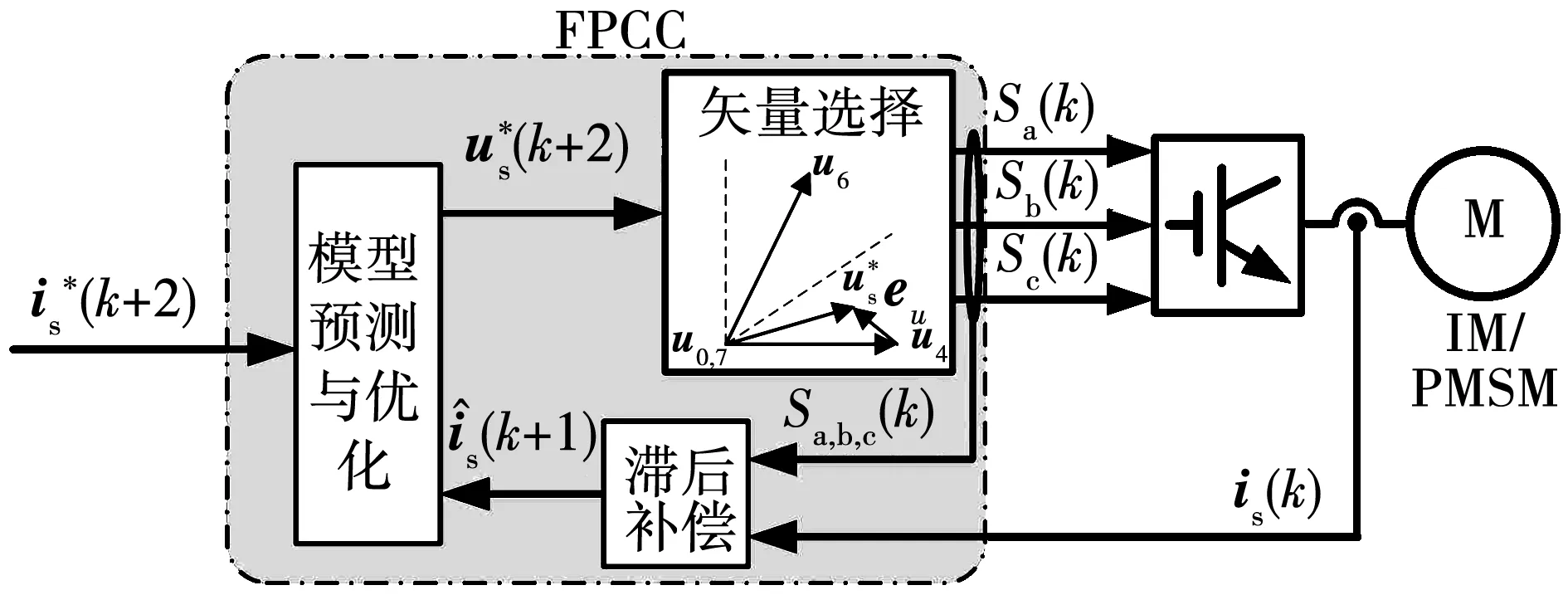
图4 FPCC原理
传统双矢量MPCC也存在双矢量组合并非最优解的问题。文献[33,41]先采用类似无差拍控制的方法得到参考矢量,然后通过使非零矢量与参考矢量之间的误差最小化来计算占空比,从而形成双矢量MPCC I算法。为了进一步减小电流纹波,将双矢量中的第二矢量放宽到可以取任意基本矢量,即可构成双矢量MPCC II算法[42]。双矢量MPCC I算法和双矢量MPCC II算法均采用类似无差拍的预测和优化方法,预测和优化的计算量明显下降。采用这种预测和优化算法虽然可以减少计算量,实现快速优化,但也存在无差拍控制固有的问题,即对模型参数敏感。
当变换器采用多电平拓扑结构时,开关数量急剧增加,这时必须使用快速优化算法才能实现FCS-MPC。文献[43]针对背靠背模块化多电平变换器,采用分组优化的方法明显较少了计算量,提高了计算速度。
2.1.3 多步预测
长预测域控制是FCS-MPC在不降低动态特性的条件下,提高静态特性和稳定性的有效方法[44]。但常用的枚举法计算量与预测域长度成指数关系,增大预测域长度将导致计算量急剧上升。针对该问题,T.Geyer在大功率中压电机控制中,提出了基于外推策略的多步预测控制方法[45]。
外推策略定义了开关域Ns和预测域Np,Ns长度一定而Np长度可变,且Ns≤Np。该策略的基本思想是先在Ns中寻找可以让被控变量处于给定滞环范围内的候选开关序列,然后通过评价函数对这些候选序列进行优化,最终得到能够使被控变量误差最小且满足一定优化指标的最优开关序列。采用该策略的方法主要包括:模型预测直接转矩控制(model predictive direct torque control,MPDTC)[46-47]和模型预测直接电流控制(model predictive direct current control,MPDCC)[48-49]。文献[50]针对五电平有源中点嵌位电路,利用MPDTC实现了对中压三相感应电机转矩和磁链的控制,并对开关频率、中点电压波动等指标进行了优化。文献[51]针对模块化多电平变换器,利用MPDCC实现了对负载电流的控制,并对开关频率、电容电压波动以及环流进行了优化。为了提高MPDTC和MPDCC方法的计算效率,文献[52]采用分支定界法实现了对Ns域内开关序列的搜索。此外,MPDTC和MPDCC还会遇到优化问题不可解的情况,即死锁。文献[53]讨论了避免死锁的方法。MPDCC原理如图5所示。
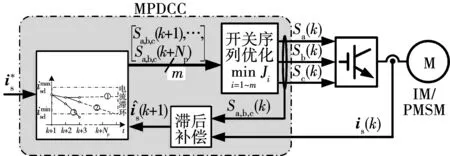
图5 MPDCC原理
为了进一步提高长域预测的计算效率,T.Geyer提出了多步直接模型预测控制[44,54-55]。该方法利用球解码算法大幅减小了长域预测的计算量。多步直接模型预测控制的评价函数由被控变量的误差和开关函数构成,这种类型的评价函数需要通过求解整数二次规划(quadratic programming,QP)问题实现优化。球解码算法通过将整数QP问题描述为截断整数最小二乘问题,基于分支定界法,以递归形式实现优化。
2.1.4 无模型预测
MPC通常需要利用精确的参数模型实现预测和优化,其主要不足是计算量较大,对模型和参数依赖性较强。
Cheng-Kai Lin等利用FCS-MPC控制频率高的特点,提出了无模型预测电流控制(model-free predictive current control,MFPCC)[56]。当控制频率较高且当前控制周期中的开关矢量不变时,可以认为当前控制周期中的电流是线性变化的,因此可以通过在一个控制周期中测量两次电流来计算其间的电流变化。其他开关矢量在一个控制周期中产生的电流变化可以用最近的历史值近似。这样,就可以在不使用电机参数模型的条件下,得到当前控制周期中所有开关矢量产生的电流变化,从而可以利用枚举法实现优化,大大提高了对模型和参数的鲁棒性。这种方法的主要不足是:需要在一个控制周期内实现两次电流采样,而且要精确控制两次电流采样的时刻,实现有一定难度。MFPCC原理如图6所示。
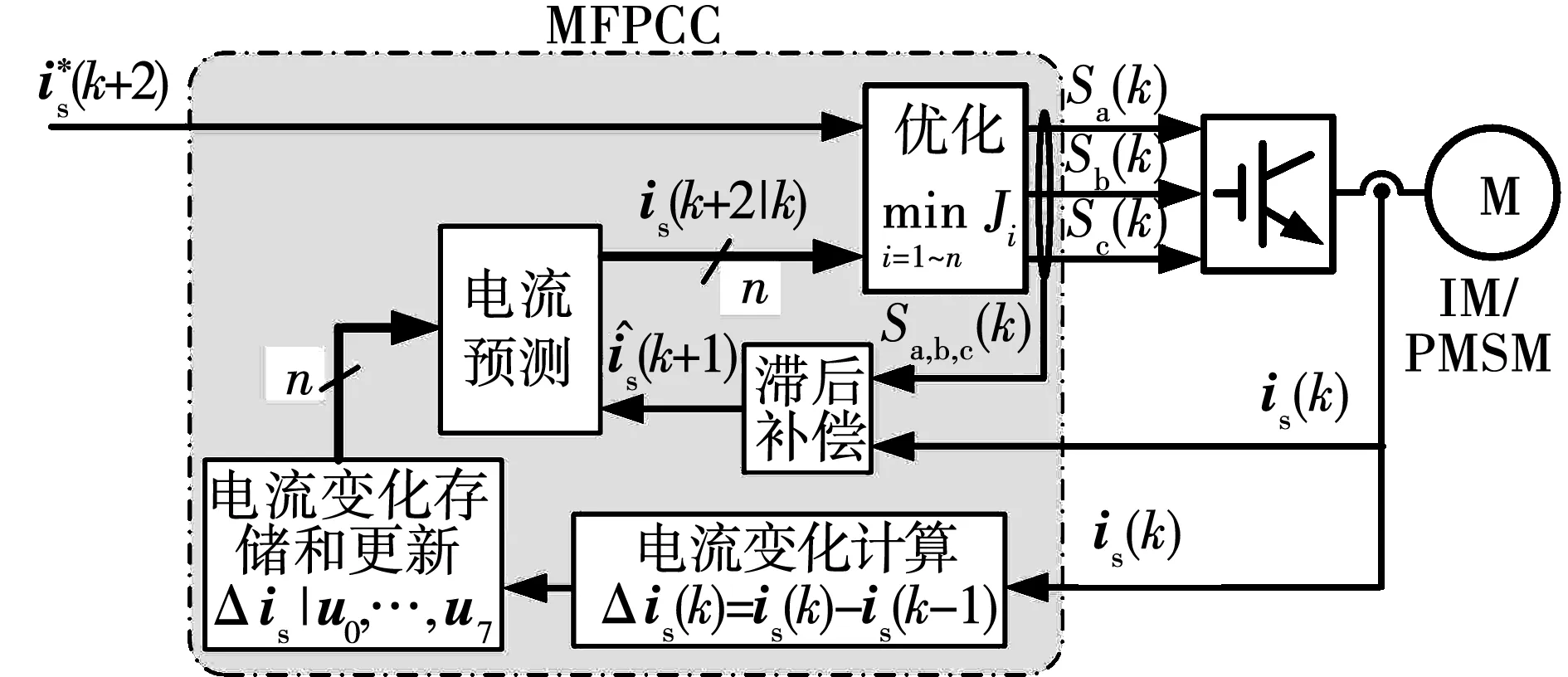
图6 MFPCC原理
针对上述无模型预测电流控制方法存在的问题,张虎和张永昌等提出了一种只需要一次电流采样的无模型预测电流控制方法[57]。该方法利用相邻两个控制周期的电流采样值实现对电流变化的计算,然后按照MFPCC的思路实现优化和控制。
2.1.5 鲁棒FCS-MPC
FCS-MPC针对有限的开关矢量完成优化,提高了控制的鲁棒性,但该方法仍然会受到模型参数误差的影响。提高FCS-MPC的参数鲁棒性已经成为交流电机控制领域研究的热点问题[11]。
文献[58]采用广义比例积分观测器(generalized proportional integral observer,GPIO)估计扰动,提高了感应电机PCC的鲁棒性。文献[59]针对感应电机,采用全阶滑模观测器和降阶滑模观测器,分别估计电流、磁链以及转速,实现了鲁棒PTC控制。文献[60]针对永磁同步电机(permanent magnet synchronous machines,PMSM),采用预测误差校正的方法提高了PCC的鲁棒性。该方法认为每个基本矢量预测误差在短时间内变化都不大,把这些基本矢量最近的误差都记录下来,就可以实现补偿。但这个方法无法从原理上消除因参数误差导致的静态误差。采用GPIO的PCC原理如图7所示。

图7 采用GPIO的PCC原理
2.2 连续控制集模型预测控制
以预测模型和优化方法的区别作为标准,可以得到CCS-MPC的分类如图8所示。下文根据该分类说明CCS-MPC在交流电机控制领域的历史发展和现状。
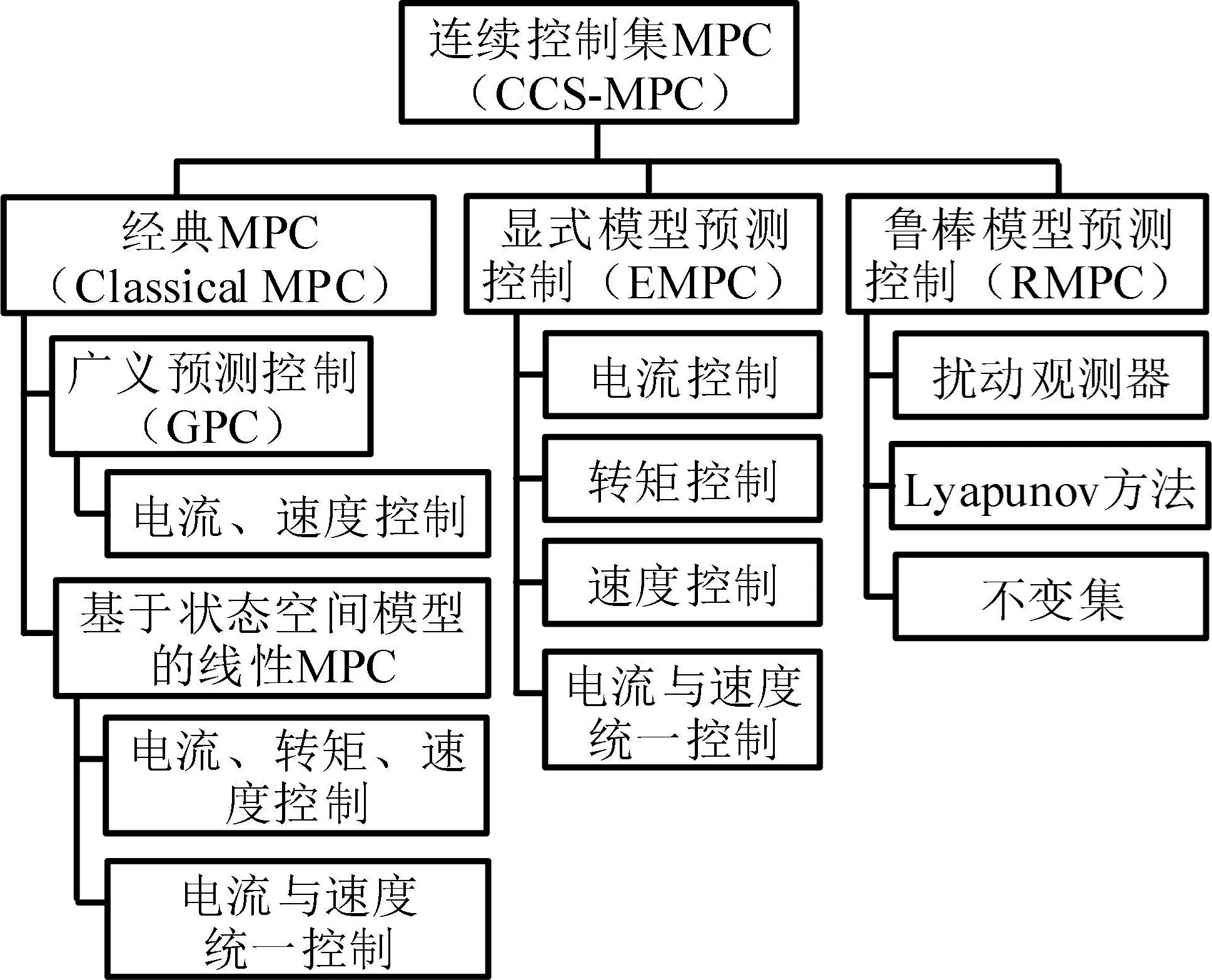
图8 交流电机中CCS-MPC的分类
2.2.1 经典MPC
用于交流电机控制的经典MPC主要包括广义预测控制(generalized predictive control,GPC)和基于状态空间模型的线性MPC。
Clarke等在1987年提出了GPC[61],该方法是一种较早用于交流电机控制的模型预测控制方法。1995年,P. Boucher利用GPC实现了对无刷直流电机的速度控制[62];1996年,D.Dumur利用GPC实现了对感应电机的双环控制[63]。此后,GPC还被用于永磁同步电机电流控制[64]、感应电机位置控制[65]以及永磁同步电机的位置控制[66]等。采用GPC的感应电机电流控制原理如图9所示。
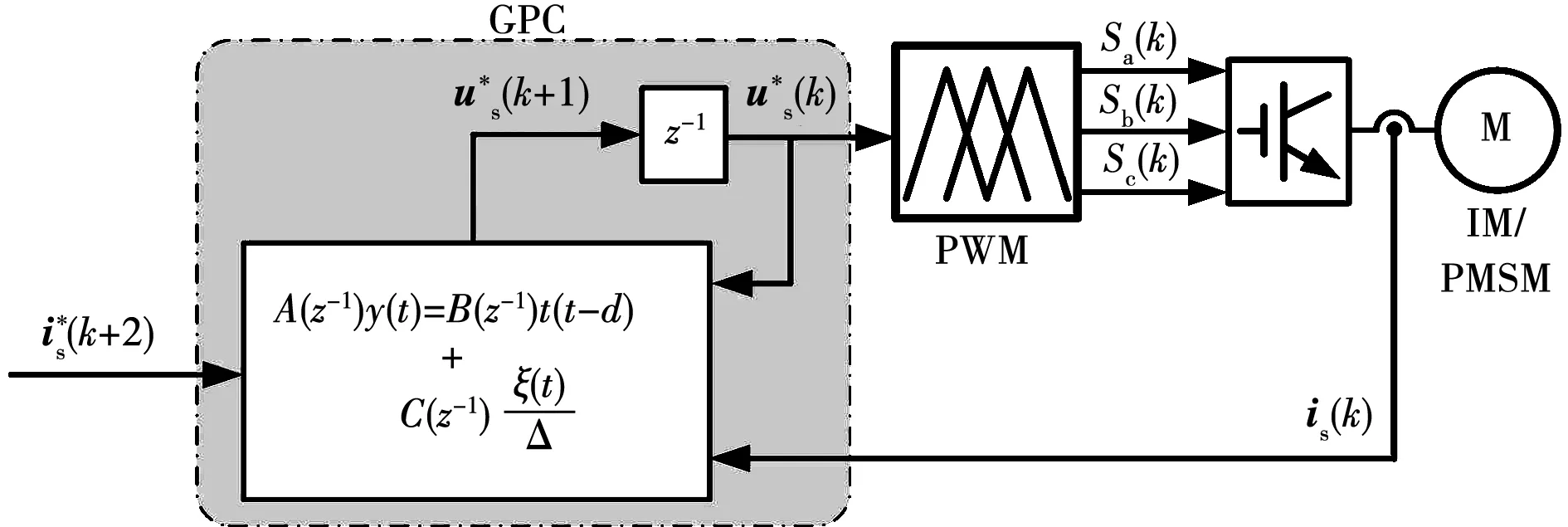
图9 采用GPC的电流控制原理
CRARMA模型多用于SISO系统,处理MIMO系统控制问题时的形式较为复杂,应用有一定难度[67];此外,MPC是一种典型的时域控制方法,状态空间模型相对传递函数模型更容易理解和应用。因此,基于状态空间模型的线性MPC在交流电机控制中得到了更多应用。这种方法常采用电机的状态空间模型和二次型评价函数实现预测和滚动优化。不考虑约束条件时,该方法可以通过离线求解QP问题得到控制变量的解析最优解;考虑约束条件时,则需要利用有效集等方法,在线求解包含约束条件的优化问题。
1997年,K. Hentabli等提出了利用基于状态空间模型的线性MPC控制三相感应电机电流和转速的方法,并给出了仿真结果[68]。此后,该方法还被用于实现感应电机电流控制[69-71]、感应电机的速度控制[72]、具有弱磁控制特性的永磁同步电机电流控制[73]、永磁同步电机的电流与速度统一控制[74]等。基于状态空间模型的线性MPC电流控制原理如图10所示。
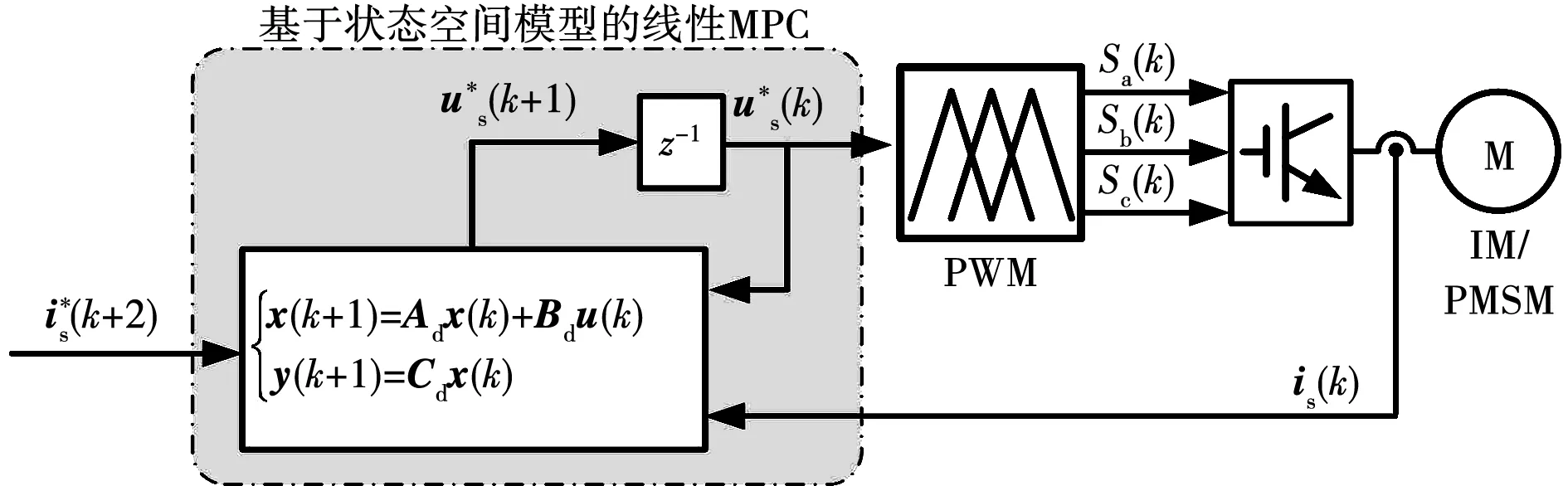
图10 基于状态空间模型的线性MPC电流控制原理
上面给出了一些线性MPC在交流电机控制领域的典型应用。此外,还有一些将线性MPC与其他方法组合起来,构成混合控制方法的特殊应用。T.Geyer针对中压感应电机大功率传动,将线性MPC与优化脉冲模式(optimal pulse patterns,OPPs)结合在一起,提出了模型预测脉冲模式控制(model predictive pulse pattern control,MP3C)[75]。该方法采用定子磁链误差以及最优开关时刻修正值构成评价函数,实现了对OPPs开关时刻修正值的优化,有效控制了定子电流的总谐波畸变率(total harmonics distortion,THD),并实现了对感应电机的转矩和磁链控制。文献[76]将MP3C用于五电平三相逆变电路,实现了对中压感应电机的转矩和磁链控制。
线性MPC常采用真实值模型实现预测,因此容易受到模型参数误差的影响,导致控制性能下降(例如产生静态误差等)。同样是因为容易受到参数误差影响的原因,线性MPC不能简单采用两步预测实现滞后补偿,否则会使其参数鲁棒性进一步下降。此外,考虑约束条件时的在线优化算法比较复杂,这也是线性MPC应用中存在的主要问题。
2.2.2 显式模型预测控制
为了解决线性MPC在线优化算法复杂、计算量大的问题, A.Bemporad和M.Morari等在2000年提出了显式模型预测控制(explicit model predictive control,EMPC)[77]。该方法实现了线性定常系统MPC优化的准离线计算。与传统求解QP问题的算法不同,EMPC将状态变量看作参数向量,从而将QP问题转化为多参数二次规划问题(multiparametric-QP,mp-QP),通过分段仿射(piecewise affine,PWA)变换得到显式状态反馈解。
2005年,A.Linder和R.Kennel等将EMPC用于感应电机电流控制[78]。其后,EMPC还被用于PMSM的电流控制[79]、PMSM的电流和转速双环控制[80]、感应电机电流控制[81]、感应电机转矩和转速双环控制[82]、双质量驱动系统的机械共振抑制[83]等。采用EMPC的感应电机电流控制原理如图11所示。
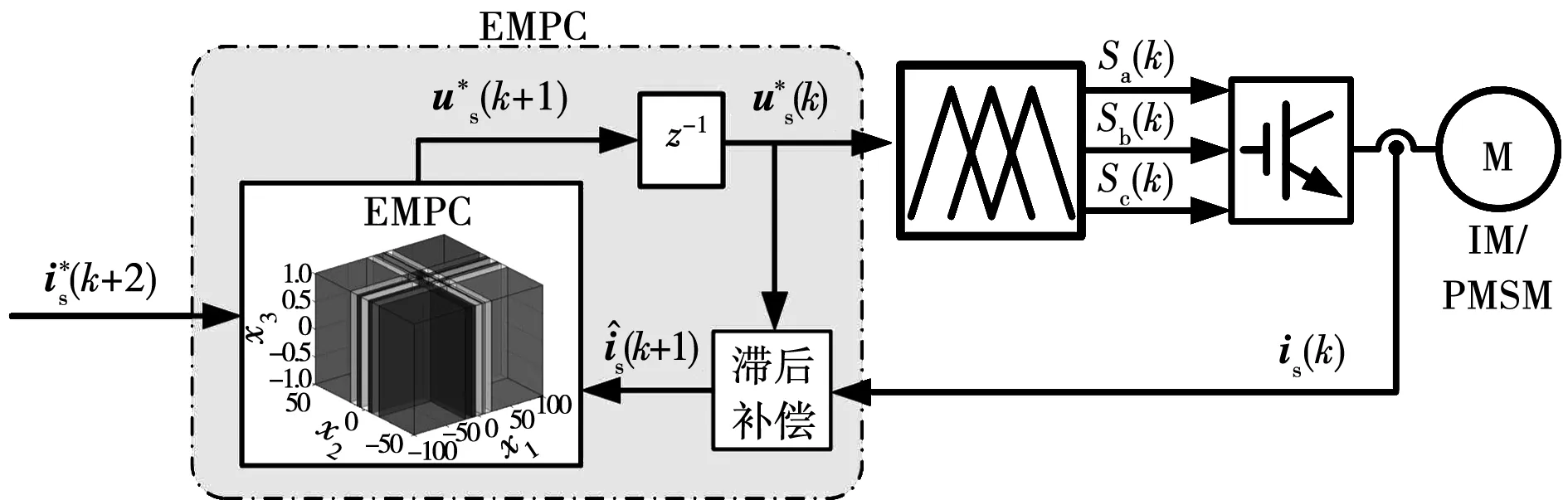
图11 采用EMPC的感应电机电流控制原理
EMPC最大的优势是可以离线完成绝大部分QP求解工作,即根据约束条件以及MPC的参数划分可行域,并针对不同的区域确定状态反馈控制律。因此,EMPC通常用于线性定常系统控制。当遇到时变系统时,EMPC会遇到重新划分区域并确定反馈控制律的问题。此外,当预测域较长时,EMPC还会遇到区域划分数量太多,实现困难的问题。
2.2.3 鲁棒模型预测控制
传统线性MPC及EMPC没有考虑参数误差和扰动对控制的影响,参数鲁棒性不强。因此,如何提高控制的鲁棒性就成为交流电机控制领域CCS-MPC研究的关键问题。理论研究领域中,提高CCS-MPC稳定性的常用方法包括:min-max优化、鲁棒收缩约束、鲁棒终端不变集、闭环预测[84]等。CCS-MPC实现无偏差控制的主要方法包括扰动观测器以及采用速度形式的模型等[85]。
文献[86]采用自适应扰动观测器实现了感应电机电流的鲁棒MPC(robust MPC,RMPC)控制;文献[87]采用增量观测器和增量模型提高了感应电机电流控制的鲁棒性;文献[88]针对PMSM,采用增广观测器估计电流和因电感误差导致的电压误差,实现了鲁棒电流预测控制;文献[89]针对PMSM,采用Lyapunov方法和控制不变集,提高了CCS-MPC的鲁棒稳定性;文献[90]针对PMSM,采用参数在线辨识的方法减小了电流控制的静态误差,但该方法需要针对不同参数设计相应的辨识方法,实现比较复杂,而且无法从原理上消除控制的静态误差。基于扰动观测器的鲁棒模型预测控制原理如图12所示。

图12 基于扰动观测器的鲁棒模型预测控制原理
表1从控制能力、计算量、性能等方面给出了FCS-MPC与CCS-MPC的比较。此外,文献[91-95]也给出了不同类型MPC间的比较,文献[96]讨论了不同类型MPC之间的联系。

表1 FCS-MPC与CCS-MPC特性对比
3 应用中的关键问题及解决方法
近三十年间,MPC在交流电机控制中取得了较大进展,建模方法、在线优化方法等不断完善,并已经在电流控制、磁链及转矩控制、速度控制以及位置控制中获得了较多研究和应用。尽管进展明显,但MPC应用中仍然存在一些问题需要进一步研究和完善,例如:如何进一步提高控制的静态特性,消除控制偏差;如何更好地解决数字控制系统的滞后问题,提出性能更好的滞后补偿方法;如何提高控制的参数鲁棒性;如何设计MPC的参数(权重系数、预测域长度以及控制域长度)等[11,20]。
3.1 无偏差控制
MPC以模型为基础实现预测和优化,建模误差、模型参数误差、扰动等因素都会导致预测产生误差,进而影响MPC的控制性能,产生控制偏差等问题[97]。
MPC理论研究领域中,无偏差控制问题得到了较好的研究,开环估计补偿、扰动观测器以及增量式增广模型方法是MPC常用的无偏差控制方法[85]。交流电机控制领域中,由于多数MPC控制方法都直接采用电机的真实模型实现预测和控制,并没有采用消除预测及控制误差的措施和方法,该问题还需要进一步研究[11]。
文献[69]和文献[98]分别采用开环估计补偿方法实现了对三相感应电机的电流控制和弱磁控制。该方法容易实现,可以在一定程度上减小MPC的控制误差,但无法从原理上消除控制偏差[97]。此外,该方法需要单独设计补偿矩阵,但补偿矩阵还没有成熟的设计方法。
扰动观测器是MPC消除控制偏差的常用方法,但在交流电机控制领域的应用还不常见。文献[99]采用扰动观测器实现了对三相电压型逆变器的控制。交流电机控制领域中应用时,由于需要增广状态变量,该方法存在模型阶数高、计算量大以及设计和实现复杂等问题。
此外,采用增广模型也可实现无偏差控制。文献[85]给出了其与扰动观测器方法的等价关系。该方法已经应用于三相感应电机的电流控制[71]以及三相永磁同步电机的电流控制[100]。由于采用增广模型,该方法也存在模型阶数高、计算量大以及设计和实现复杂的问题。
除上面讨论的3种方法以外,交流电机控制中的MPC还可以采用一些其他方法实现无偏差控制。文献[90]采用参数在线辨识的方法实现了三相感应电机的无偏差电流控制;文献[101]针对PMSM的无差拍电流控制,采用参数在线自适应调整的方法,在磁链参数准确时,消除了因电感误差而导致的静态误差。这类方法理论上可以消除参数误差对预测的影响,但不同的参数需要采用不同的方法辨识,导致辨识算法复杂、实现困难。此外,这类方法还难以保证多个参数均能准确在线辨识。文献[102]针对永磁同步电机速度控制,采用一个独立的积分器实现无偏差控制。这种方法容易实现,但会降低系统的动态特性,而且破坏了MPC的统一结构。
3.2 滞后与补偿
交流电机数字控制系统常采用滞后一拍的控制方式,以解决采样、计算以及占空比更新等环节时间延迟导致的最大占空比受限问题[103-104]。采用滞后一拍的控制方式时,反馈信号的采样过程与控制变量的计算和实现过程并不同步,从而导致MPC出现超调和振荡,严重时会影响系统的稳定性[105]。
多采样方法和基于模型的预测补偿方法是交流电机控制领域中两种常用的滞后补偿方法。文献[106]针对PMSM无差拍电流控制,通过单个开关周期中的两次电流采样和两次占空比更新,减小了滞后的影响,并扩展了电流环带宽。该方法实现简单,但无法从原理上消除一拍滞后产生的影响。文献[107]针对PMSM直接转矩控制,在单个开关周期内两次采样,然后利用线性插值的方法得到被控变量的预测值,实现了对一拍滞后的补偿。该方法原理简单,计算量小,但会明显减小控制算法的有效运行时间[108]。
相对于多采样方法,基于模型的预测补偿方法理论上可以完全消除滞后带来的影响且计算量不大,在交流电机控制领域的MPC中应用较多[47,109-110]。预测补偿方法主要包括开环补偿和闭环补偿两种类型。开环补偿常使用电机真实值模型直接计算被控变量在下一个控制周期的值,并将其作为预测的初始值[111-113]。该方法原理简单,常用于FCS-MPC,其主要问题是容易受到电机参数误差等因素的影响而产生补偿误差[114]。闭环补偿则采用观测器得到被控变量的观测值,并将其作为预测的初始值[115-116]。采用传统观测器补偿一拍滞后时,同样会受到电机参数误差等因素的影响,导致MPC产生控制偏差[114]。采用增量观测器[87]、PI观测器[58]、扩张观测器[88]或扰动观测器[86]均可以克服传统观测器存在的问题,提高滞后补偿的鲁棒性。
3.3 参数设计
设计MPC时,需要确定的参数较多,主要包括预测域长度、控制域长度、评价函数的形式、权重系数等。
1)预测域长度和控制域长度。
对于采用枚举法实现优化的FCS-MPC,计算量会随着预测域长度Np增加而迅速增加。因此,FCS-MPC通常采用1步或2步预测,较难实现长预测域控制。但也有例外,T.Geyer用外插的方法实现了长域预测,这时就要合理选择预测域长度[44,117]。与FCS-MPC不同,不考虑约束条件时,CCS-MPC可以得到解析形式的最优解,比较容易实现长预测域控制。
目前,还没有通用的预测域长度设计方法,常见的预测域长度设计方法包括:经验法[118]、基于事件的预测域长度设计方法[45,119]等。应用中,可以根据被控对象动态过程的时间长度来选择预测域长度。预测域并非越长越好,而是应该根据控制指标来综合选择。响应速度较快时,预测域长度可以较小。
控制域长度Nc应该包含控制变量会产生变化的所有时域范围。该参数也没有成熟、通用的理论设计方法,应用中多依靠经验来确定取值。预测域较短时,可使Nc=Np;预测域较长时,为了较小计算量,可取Nc 2)评价函数选择。 由于FCS-MPC的评价函数仅是计算开关状态对被控变量作用效果的工具,不涉及最优控制的分析和求解,选择评价函数的形式灵活多样,可以通过将多种优化目标包含在评价函数中实现多目标优化。FCS-MPC还可以通过变化评价函数形式的方法来降低权重系数的设计难度。 CCS-MPC则常采用2-范数形式的评价函数,以便实现最优控制的分析和求解。CCS-MPC较难实现多目标优化,其主要原因是加入多种优化目标后会导致最优控制难以分析和求解。 3)权重系数。 权重系数对MPC的动态性能(超调、振荡以及调节时间等)有明显影响。因此,确定权重系数的取值是MPC设计的主要任务。目前,权重系数通常需要凭借经验确定,没有成熟、统一的设计方法[11]。 启发式算法是确定权重系数最常用的方法。该算法只是一类解决问题的思路,而不是一种明确、通用的方法。这种算法基于经验,先针对具体应用定义出性能指标,然后通过大量的仿真和实验来寻找近似最优解[11,120]。该方法的特点是只能找到近似最优解,且无法得到近似解与实际最优解之间的偏差。这种方法的主要问题是仿真和实验的工作量大。 FCS-MPC的评价函数中通常不包含控制变量,等价于控制变量的权重系数为零,即对控制变量没有约束,这样会得到较高的动态响应速度,但容易使被控变量产生更大的纹波。由于FCS-MPC的评价函数中通常只包含被控变量相关的优化项,且可以灵活选择评价函数的形式,使其能够采用多种方法实现权重系数设计,常用的方法包括:当评价函数中的优化项是同一类型物理量时,不需要设计权重系数[40,121];将评价函数中不同类型的物理量转化为同一类型,可以避免设计权重系数[122];将包含多个物理量的复杂评价函数分解成多个仅包含单个物理量的简单评价函数,采用顺次优化的方法避免设计权重系数(sequential model predictive control,SMPC)[123-124];采用多评价函数和模糊逻辑来确定权重系数[125]等。 CCS-MPC采用的评价函数与FCS-MPC不同,不但含有被控变量相关的优化项,还含有控制变量的优化项(用于限制控制变量的幅值或增量)。即使CCS-MPC的被控变量是同一类物理量,也不能采用与FCS-MPC类似的无权重系数设计方法。因此,CCS-MPC的权重系数设计方法灵活性较低。启发式算法是CCS-MPC最常用的权重系数设计方法。文献[126]针对三相感应电机电流控制,以系统闭环模型为基础,建立了设计参数与系统动态性能指标之间的关系,提出了权重系数、预测域长度、控制域长度的半解析参数设计方法。该方法可以根据动态性能指标直接计算MPC参数,大幅度减少参数设计所需的仿真和实验工作量。 交流电机控制中,MPC的分析和设计通常在理想情况下完成,不考虑参数误差的影响。实际应用中,电机参数测量通常存在误差,某些电机参数还会受环境影响而发生变化(例如:电机定、转子电阻随环境温度升高而增加,磁场饱和导致互感及漏感变化等)。这时,MPC的性能将会受到这些参数变化的影响,出现动态特性变差、控制偏差以及稳定性下降等问题。因此,需要研究提高MPC鲁棒性的设计方法。 理论研究领域中,MPC鲁棒性研究的核心问题是如何处理不确定性因素[127]。目前,处理不确定性因素有两类基本思路。一类思路是不建立不确定因素(例如:扰动、模型参数误差等)的模型,而是在假设其有界的前提下,针对最差的情形完成设计。这种思路类似鲁棒控制,其设计结果比较保守。另一类思路是建立不确定因素的模型,利用该模型预测不确定因素的变化,并以此为基础完成优化。这类思路需要对不确定因素建模,因此也被称为随机模型预测控制(stochastic model predictive control,SMPC)。SMPC在MPC理论领域得到了广泛研究,并产生了很多分支和方法[128]。 交流电机控制中,提高鲁棒性仍然是MPC研究的热点问题[11],参数在线辨识、预测误差反馈校正是主要的方法。文献[60]通过预测误差比例反馈校正提高了预测电流控制的鲁棒性,该方法虽然能提高PCC的鲁棒性,但无法实现无偏差控制;文献[129]通过预测误差积分补偿实现了PMSM的鲁棒PCC,该方法可以实现无偏差控制,但会降低系统的动态特性;文献[90]采用参数在线辨识和校正的方法实现了感应电机无偏差电流预测控制。除了上述方法外,还可以采用扰动观测器实现鲁棒MPC;文献[130]采用扰动观测和补偿实现了感应电机的转矩控制;文献[86]采用自适应扰动观测器实现了PMSM的电流控制;文献[58]采用广义比例积分观测器实现了感应电机的鲁棒PCC;文献[88]采用增量模型和扩张观测器实现了PMSM的电流预测控制。此外,文献[89]采用控制不变集和Lyapunov函数实现了PMSM的鲁棒MPC控制。 本文针对交流电机控制,梳理和归纳了MPC的现状和发展,可以得到如下结论和展望: 1)理论方面,建立了较为完整的研究体系,MPC基本的设计方法与流程逐渐成熟;控制偏差、稳定性、鲁棒性等基本理论问题得到了研究;EMPC、约束搜索等新型在线优化算法得到研究,在线计算速度和效率得到提高;MPC开始与模糊控制等其他现代控制方法结合使用,构成了更加有效的控制方法。此外,不同类型MPC之间的联系以及比较也得到了一定的研究。 2)应用方面,从仅利用MPC取代多环结构中的控制器,逐渐发展到采用MPC实现统一控制、直接转矩控制等。此外,MPC还扩展到矩阵变换器驱动交流电机[131-132]、双三相电机和多相电机控制[133-136]、多相电机容错控制[137-138]以及多电平变换器驱动交流电机的控制[139-140]等应用。 3)稳定性分析与设计、鲁棒性分析与设计等问题在结合应用领域特点的基础上还没有得到充分研究,理论研究与应用之间还存在较大差距;虽然形成了较为完整的设计方法和流程,但参数(预测域长度、权重系数等)设计方法等问题仍然没有得到很好解决,多数参数仍然需要依靠经验以及实验来确定;控制方法实现时,仍然存在计算量大、计算速度慢等问题,需要采用更先进的快速算法以及FPGA等计算能力更强的芯片来实现。这些都是未来需要进一步研究的内容。3.4 鲁棒性设计
4 结 论

