深入本质 立足建模 提升思维
——“用一元一次方程解决利润问题”的教学与思考
付小飞
(江苏省苏州市第十六中学校 215003)
《义务教育数学课程标准(2022年版)》在核心素养的主要表现及其内涵中明确指出:“初步感知数学建模的基本过程,从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律”[1].方程的本质是描述现实世界中的等量关系,更形象地说,用等号连接两种不同的表示方法表达相同或相等的量,用方程解决问题在初中阶段对培养学生数学建模能力起着至关重要的作用.但是在实际的教学过程中,有些教师习惯于将方程的应用根据题目的实际背景分成不同类型,先分析类型特征、归纳常用等量关系,再通过例题示范、变式训练来教学.新课的教学不知不觉就变成了习题课,大量的变式题排山倒海而来,这种教学方式不仅没有抓住方程的本质,还会多出大量的所谓解题的“套路”,一旦遇到“非标准”的类型时,学生就会束手无策,长此以往不利于学生思维水平的提升.带着这些问题,笔者对苏科版七年级上册“用一元一次方程解决利润问题”作了全新的教学设计,并在全市上了一节示范课,得到了与会专家和教师的高度评价.现对其主要的教学环节进行介绍,并且给出各环节的教学分析以及教学建议,以供同行参考.
1 创设情境,引入新知
活动1 在刚刚过去的“双11”购物节中,小明以每个20元的价格进了一批玩具,贴上每个30元的标签,为了吸引顾客,打出“大酬宾,九折优惠”的广告,则进价是元,标价是元,售价是元,利润是元,利润率是.
问题1:你能列举打折促销中的哪些常用量?
问题2:说出商家从进货到销售的过程中涉及哪些量?你能写出各个量之间的关系吗?
问题3:售价有几种表示方式呢?
教学分析与建议在课前可以让学生做一次社会调查,体会商品销售问题中的现实情境,收集各种打折销售的活动方式.有了真实的体验,可进一步帮助学生更深刻地理解相关术语.然后再通过问题情境,通过具体的数字,利用销售流程(图1)和柱状图(图2)理清销售问题各个量之间的关系,并且归纳出售价的两种不同表示方法.这种设计从学生已有的知识经验出发,通过创设实际的生活情境,将学生所学的数学知识与生活实际相联系,从而激发学生的求知欲望.

图1 图2
2 数形探究,分析问题
活动2 商店将进价为140元的商品按标价的8折销售,仍可获利28元,问商品的标价为多少元?
师:如果设标价为x元,有几种列式的方法?
生1:0.8x=140+28.
师:请解释一下方程两边所表示的意义.
生1:左边的式子表示售价,右边的式子也表示售价.
师:有没有列方程的其他方法?
生2:0.8x-28=140,左边的式子表示进价,右边的式子也表示进价.
生3:0.8x-140=28,左边的式子表示利润,右边的式子也表示利润.
生4:我用的是小学学的算式的方法,(140+28)÷0.8.
师:如果左边用x表示,则可以得到x=(140+28)÷0.8,实际上这也是一个方程.
生4:左边表示的是标价,右边也是标价.
师:上面列出几种不同的方程,方程的两边都是表示同一个量,因此我们在列方程解应用题时,可以利用题目中某些量的两种不同表示方法来列方程.

图3
学生讨论过程中教师巡视,借助销售条形图(图3)引导学生列出不同的方程.
教学分析与建议在初中阶段用方程解决实际问题时学生“最大的痛点”就是无法将实际问题中各个量用代数语言描述并构建方程.如果教师仅仅告诉学生要通过审题,找出等量关系,再列出方程,那么对于学生来说是比较含糊的,容易使学生望而生畏.因此在教学时教师要给学生指出一个明确的方向,告诉学生列方程实质上就是用两种方式表示相同或相等的量.例如活动2中,可从以下几个方向思考:
思考1 以两种方式表达进价,即0.8x-28=140 ①;
思考2 以两种方式表达利润,即0.8x-140=28 ②;
思考4 以两种方式表示售价,即0.8x=140+28 ④;
思考5 以两种方式表示标价,即x=(140+28)÷0.8 ⑤.
通过以上几个方程的列出过程,我们可以发现题目中给出的任何一个量都可以用两种不同方式来表示,要得到方程就是“信手拈来”,这样为学生用方程解决实际问题指明了方向.同时利用图表的示意作用让思维可视化,解除了学生的畏难心理.
尤其对于方程⑤,如果把右端的x抹去,就是小学时的算术解法.而当学生提出用算术的方法时,如果教师直接告诉学生算术解法不如列方程来得简洁,这时学生就会产生疑惑.初一的学生正面临从算术思维向代数思维过渡,我们可以通过比较算术方法和方程方法的优劣性,让学生体会从算术到方程的通性,学生自然就可以从小学的算术思想过渡到方程思想.
3 典例示范,内化新知
活动3 一件夹克衫先按成本提高50%标价,再以8折出售,结果获利28元,这件夹克衫的成本价是多少元?
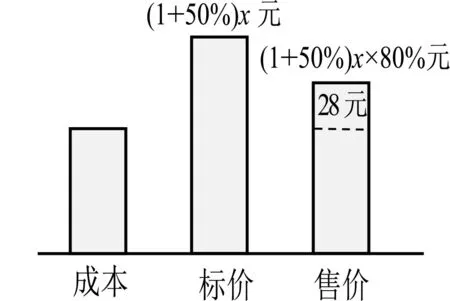
图4
师:销售这件夹克衫涉及哪些价格?
生1:成本、标价、售价.
师:说得很好!如果设这件夹克衫的成本是x元,我们可以从中找出的等量关系是什么?(生讨论发言)
师:在实际操作中,我们可以画线性示意图或画柱状示意图.
师:获利28元是从哪里来的?(生讨论发言)
师:从柱状示意图(图4)中,可以得到的相等关系是什么?
生:发现售价有两种不同的表示方法,这两个代数式相等,即为等量关系.
(学生做,教师用多媒体演示)
师:请大家做完后想一想,还有没有其它的量可以用不同方法表示,从而得到方程?如果有,哪一个列式方法相对简单?
教学分析与建议本活动的重点是借助柱状示意图寻找各个量之间的数量关系,尝试多种方法列方程后,引导学生合理选择要表达的量作为列方程的依据,突破“找等量关系”这个难点.在实际教学中,在给学生充分时间思考后,学生给出了多达8种不同的列方程的方法,通过分析比较,让学生理解为什么在这个问题中以售价作为要表达的量最为简捷.这就好比A要从甲地(题中的已知)送物品给乙城的B(题中设为x的未知量),最为节省时间的方法就是A,B约定同时到两地之间某个地点来交换物品.而售价就好比A,B两人相约的地点.相当于列方程时我们思考的工作量被分成了两段,就是分别用进价和标价来表示售价,然后用等号连接就得到方程.而小学算术解法中的算式,就相当于是A到乙城直接送交到B手中,思维上要求就更高一点.所以快速准确地找到最合适的表达量来列方程,可大大减少思考的难度.
4 自主学习,类比理解
活动4 请以下列方程各编写一道关于商品利润的应用题:(1)140(1+x)=210×80%,(2)140+28=210x.(学生合作交流)
生:商店将进价为140元的商品标价为210元,打八折销售后,利润率是多少?
生:商店将进价为140元的商品标价为210元,问商品打几折销售后可获得28元的利润?
师:你能说出方程两边表示的实际意义吗?
生:方程(1)和(2)左右两边都是表示售价,左边是用进价表示,右边是用标价表示.
教学分析与建议通过分小组讨论,自编题目,互评互检,并引导学生说出方程两边分别表达的量的意义,强化用两种方式表达同一个量来列方程的解题思路.让学生从多个方向、多个层次进行思考,
从而提升思维水平.同时,让学生自己设计习题,也能更好地锻炼学生的建模能力,当学生面对自己“创造”出的习题更感兴趣时,练习也就更投入了.
5 合作探究,提高技能
活动5 某件商品因换季准备打折出售,如果按标价的七五折出售将赔25元;而按标价的九折出售将赚20元,问这件商品的标价是多少?

图5
师生活动:让学生独立思考后,通过以下问题串,引导学生选择用合适的量作为目标来建立相等关系列方程:
(1)题目中涉及到几种价格?
(2)你能否准确设出未知数?
(3)你能否画出本题中的柱状示意图?
(4)你能否用不同的方式来表达这个量?
(5)你认为选哪一个量作为列方程的依据最为简单?
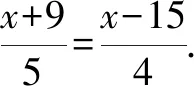
列方程解决实际问题的学习对学生以后学习分式方程、不等式以及函数都有一定的启发作用,所以学生学习本章的结果将直接影响学生对后续内容的理解与掌握.《义务教学数学课程标准(2022年版)》要求“应当让学生经历对现实问题中量的分析,借助用字母表达的未知数,建立两个量之间关系的过程,知道方程或不等式是现实问题中含有未知数的等量关系或不等关系的数学表达;体会算术与代数的差异.”[1]基于这些原因,在教学设计的过程中,务必力求做到从学生已有知识经验出发,注重新旧知识的联系,恰当地使用信息技术,做到一题多解,重视展示思维过程,让学生通过比较来感悟方程解决问题的优越性,从中了解和体会数学地研究问题的思路与方法.

