高分辨率桥梁裂缝图像实时检测
刘信宏,苏成悦,陈 静,徐 胜,罗文骏,李艺洪,刘 拔
(广东工业大学 物理与光电工程学院, 广东 广州 510006)
混凝土结构桥梁的裂缝会破坏桥梁结构整体性[1],甚至引发坍塌事故,定期巡检桥梁具有必要性。国内外学者对桥梁裂缝检测做了大量研究,如kmeans结合区域生长[2]、裂缝发展趋势估算的思想[3]、基于局部纹理的检测算法[4]、使用支持向量机、自适应提升(Adaboost) 和随机森林的分类模型[5]、照度补偿模型和裂缝概率图[6]等。在统计信息网格聚类的思想下,结合区域生长算法,取得了较好的裂缝提取效果[7],但其网格聚类环节中,容易选取到背景区域。应用多尺度Hessian矩阵可降低纹理干扰,较好地抑制背景,增强裂缝[8]。但上述研究都没有考虑算法的实时性,无法应用于嵌入式平台。多尺度的方向滤波器,降低了光照及背景干扰,能在主机端进行较低分辨率实时检测[9]。Canny边缘和区域生长的思想可实现快速裂缝分割[10],但抗干扰能力不足。还有运用UNet模型[11]、全连接网络[12]和卷积神经网络[13-15]等深度学习的方法,跳过特征描述的过程,实现端到端的识别,其依赖于大量的数据集和图形处理器支持,在移动平台较难实现在线实时检测。
本文提出一种嵌入式平台上高分辨率裂缝图像的实时检测算法。采用移动平均法[16]粗分割;通过几何特征筛选候选裂缝片段,结合区域生长修复和过滤候选裂缝片段;建立双判别准则的裂缝片段聚合模型,递归合并裂缝片段,并抑制干扰区域。
1 裂缝检测算法
本文提出的裂缝实时检测算法流程如图1所示,图中二值图黑色为前景,白色为背景。
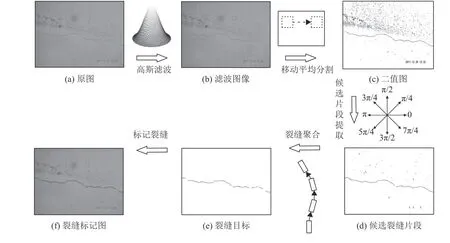
图1 裂缝识别流程图Fig.1 Flow chart of the proposed method
1.1 图像预处理
高斯滤波广泛运用于无人机图像处理、视频图像处理和图像预处理等场景[17-18]。图像噪声中大部分噪声为白噪声,使用高斯滤波器可有效降低噪声对检测的影响[19]。对输入图像进行高斯模糊,记I(x,y)为高斯滤波后的灰度图像。
桥梁裂缝图像受复杂光照环境影响,其亮度分布不均匀。受Shi等[16]的移动平均分析的启发,本文采取移动平均的分割方法,阈值由式(1) 确定。
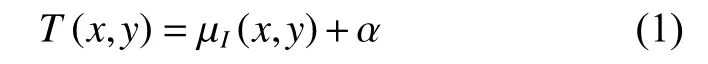
式中: µI(x,y) 为 图像I(x,y) 中尺寸为ε ×ε的滑动窗口的灰度均值,α 为偏移系数。
获取二值图像B(x,y)的分割过程如式(2) 所示,前景目标区域设为1,背景区域设为0。
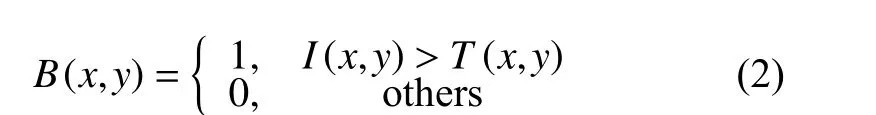
1.2 候选裂缝片段提取
候选裂缝片段提取模块如图2所示。图2(a) 为裂缝阈值分割图,通过第一次几何轮廓筛选得到图2(b)所示的种子区域,采用八方向区域生长算法获得图2(c),再进行一次几何轮廓筛选得到如图2(d) 所示的候选裂缝片段,其连通域集合记为Q={Q1,Q2,···,Qm}。
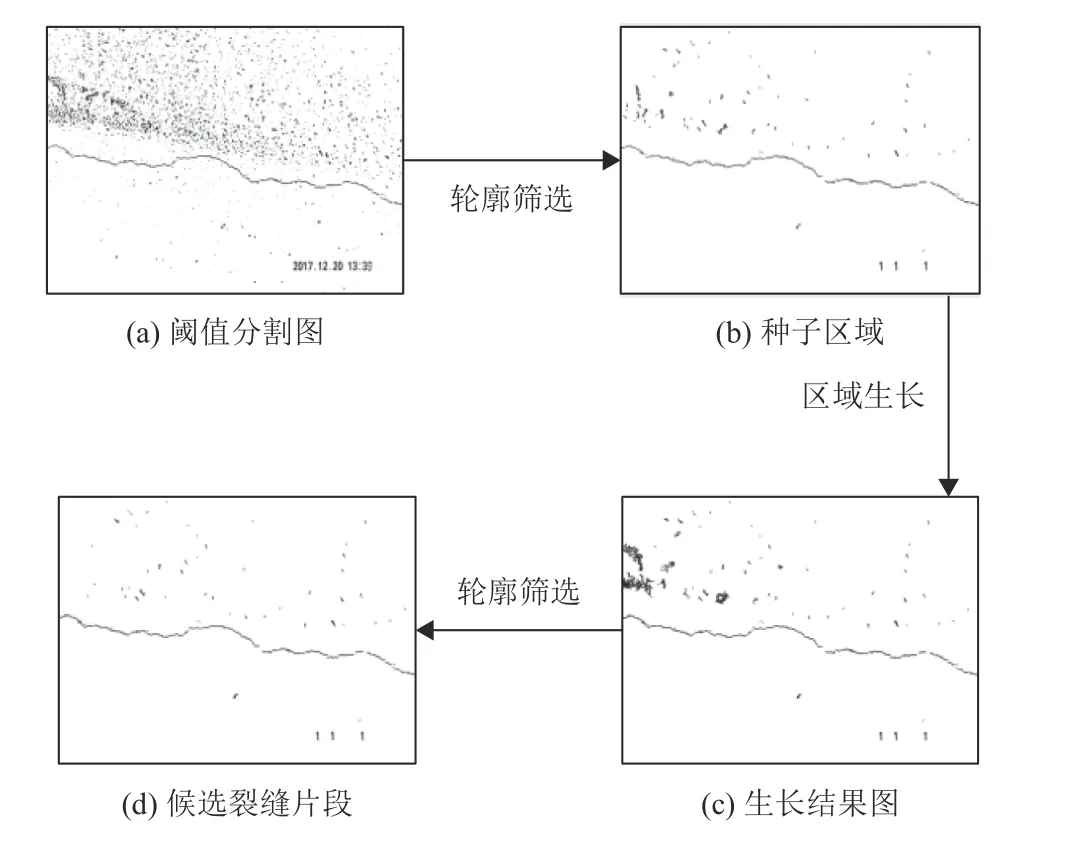
图2 候选裂缝片段提取流程Fig.2 Flow chart of candidate crack fragment sampling
1.2.1 几何轮廓筛选
裂缝片段和背景噪声具有较明显的几何特征差异,如图3所示,图3(a) 为背景噪声,其轮廓无明显几何规则;图3 (b) 为裂缝片段区域,具有明显的细长几何特征。
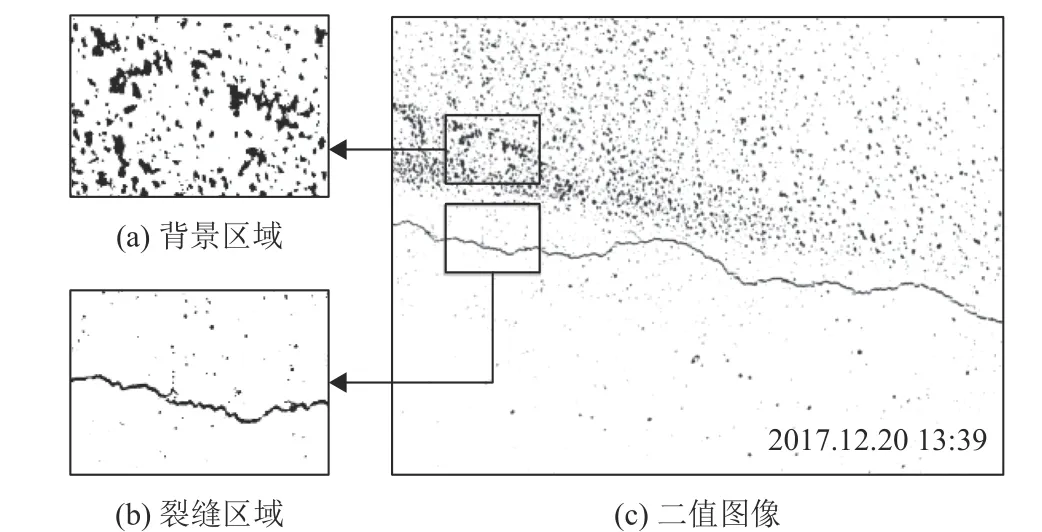
图3 裂缝与背景区域的几何特征差异Fig.3 Difference between crack and back ground region
本文采用连通域面积A和连通域轮廓的惯性率ηIR来描述连通域的几何特征。二值图像的连通域面积为图像的零阶矩,图像的二维(i+j) 阶 矩Mij的定义如式(3) 所示,则连通域面积A=M00。
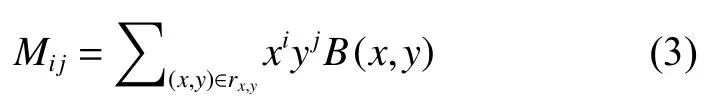
式中:i=0,1,2,···,j=0,1,2,···,rx,y为连通域内所包围的点。
惯性率可用于描述目标的伸长程度,惯性率越接近1,则越相似于圆形。惯性率可由图像中心矩得到,图像的二维(i+j)阶中心矩定义如式(4) 所示。

式中:(TAmin,TAmax)为 轮廓面积阈值范围,TIR为轮廓惯性率阈值。
1.2.2 区域生长
区域生长是依据预设的生长规则,将图像像素或者子区域合并的过程。从一组种子点开始遍历相邻像素,寻找满足预设生长规则的像素,并将其添加到种子中而形成生长区域,常用于图像分割[7,10]。

式中:Ts为区域生长灰度阈值。
3) 重复步骤1) 和2) ,直到S为空集,输出区域生长完成的二值图像B′(x,y)。
1.3 裂缝聚合
如图4所示,提取的候选裂缝不连续,且与背景干扰的形态相似。本文提出双判别准则的裂缝聚合模型,模拟裂缝延伸趋势,依据位置和方向信息构造聚合准则,递归聚合细长裂缝,并抑制背景干扰。
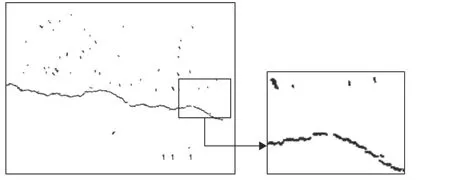
图4 裂缝片段Fig.4 Crack fragment
1.3.1 聚合准则
以裂缝片段轮廓的最大距离点对(Pb,Pf)作为裂缝片段的端点,联合裂缝片段最小外接矩形倾角V,构建裂缝片段的特征向量H=(Pb,Pf,V),其中,本文通过轮廓的上下左右4个边界点的快速枚举来近似替代Pb和Pf;使用Sklansky[20]的方法检测裂缝片段的凸包后,运用旋转卡壳法[21]处理凸包而得到的矩形,即为裂缝片段的最小外接矩形。记聚合裂缝集合为X={X1,X2,···,Xn},其中每个裂缝元素由多个裂缝片段构成。记裂缝片段最小外接矩形的长边为lw。
定义两裂缝片段Q1和Q2的距离D(Q1,Q2)为两裂缝片段的端点间的最短距离,裂缝片段的聚合准则1定义如式(8) 所示。

式中:Tdmax为长距离阈值。
定义裂缝过滤准则,如式(10) 所示。若δk=0,则将裂缝Xk剔除,否则保留该裂缝。
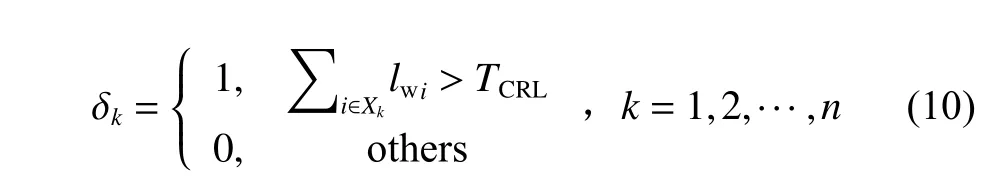
式中:TCRL为裂缝长度阈值。
裂缝片段聚合算法流程如下:
1) 计算候选裂缝片段连通域集合Q中元素的特征向量H;
2) 按m ax(Pb.y,Pf.y)降 序和m in(Pb.x,Pf.x)升序对Q排序;
3) 对Q中满足式(8) 或(9) 的元素进行聚合,输出聚合裂缝集合X;
4) 将集合X作为输入,重复步骤3) ,直到集合X和Q的元素个数相等;
5) 依据式(10) 过滤裂缝。
其中步骤3) 为算法的核心步骤,其流程如表1所示。

表1 裂缝聚合算法Table 1 Algorithm of merging crack fragments
1.3.2 裂缝聚合示例

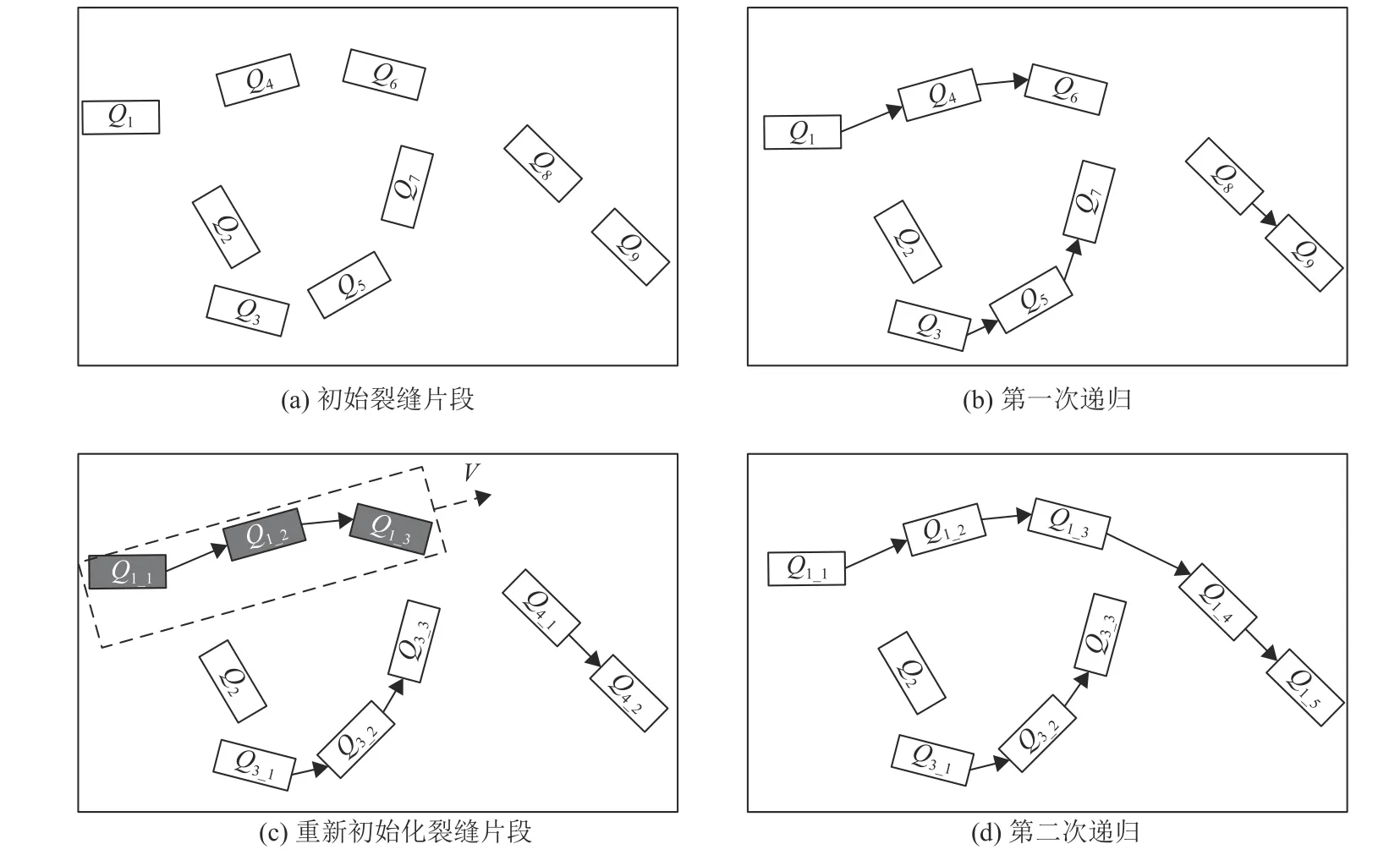
图5 裂缝片段递归聚合示例Fig.5 Sample of merging crack fragments recursively

2 实验结果分析
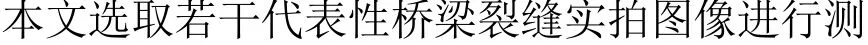


2.1 灵敏性分析及参数确定

本文算法待确定的核心参数有:轮廓惯性率阈值TIR、 区域生长灰度阈值Ts、短距离阈值Tdmin和长距离阈值Tdmax。 设参数初始值为:TIR=0.1,Ts=10,Tdmin=0.1,Tdmax=0.8,分别独立改变参数值,对数据集全部图像进行测试。分别统计准确率、召回率和F值3个指标的均值,如图6所示。图6(a) 表明,TIR在区间[0.05,0.12]范围内都有较好效果,选取F值开始下降的前一个数值0.11;图6 (b) 中,Ts=8时,F值表现最佳;图6(c) 和图6(d) 中,Tdmin和Tdmax的趋势一致,当参数值较小时,其精确度高,但召回率低,说明此时漏检严重,当Tdmin=0.35时,精确度和召回率达到均衡,而Tdmax的均衡点为0.6。故本文选取参数值为TIR=0.11,Ts=8,Tdmin=0.35,Tdmax=0.6。
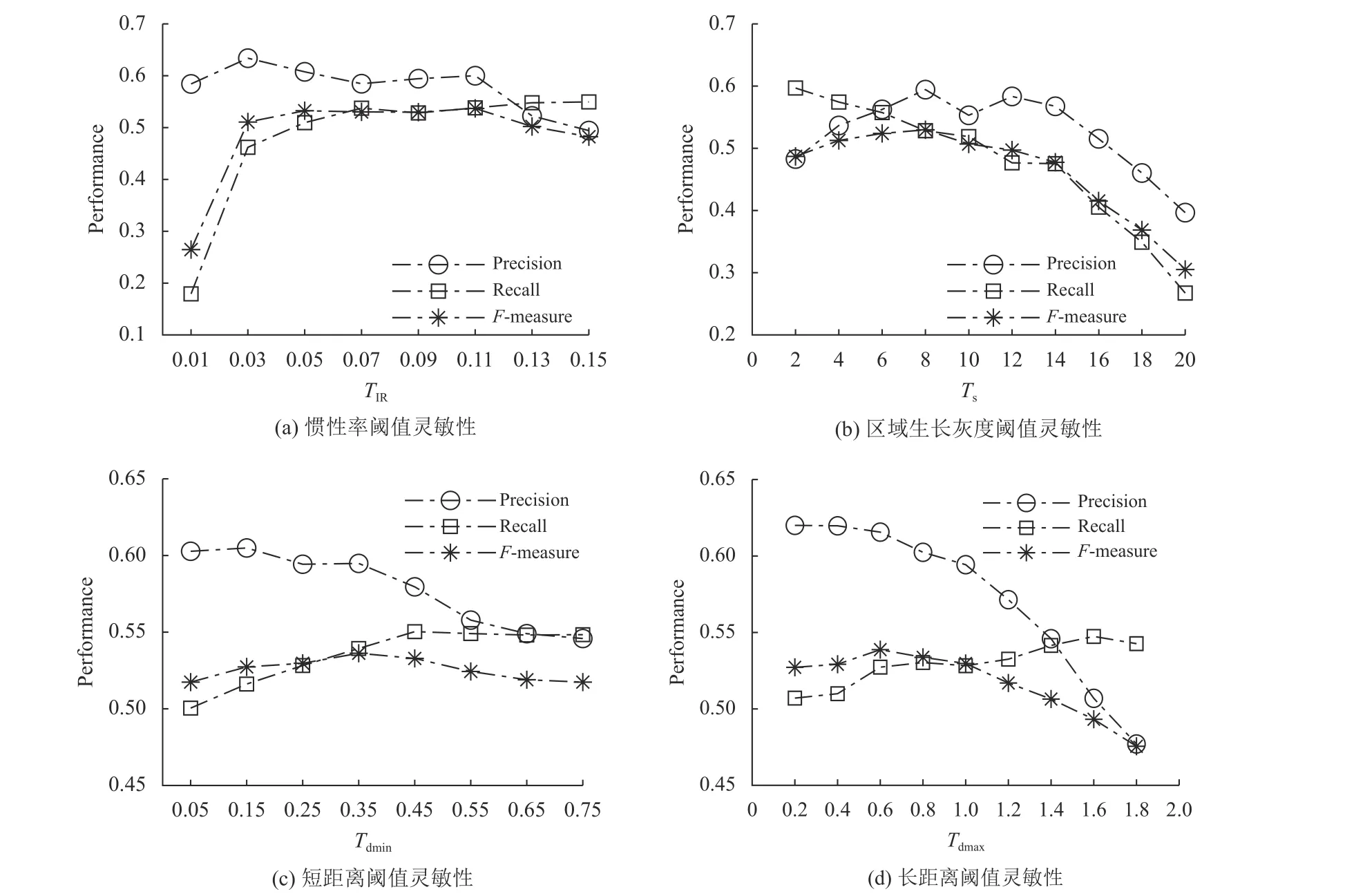
图6 参数灵敏性分析Fig.6 Parameter sensitivity analysis
文献[7]算法使用默认参数;文献[8]算法中多尺度参数 σ取值为(3,4,5,6,7) ;使用文献[10]算法时,在算法原基础上,将面积大于3 ×104的轮廓滤除。
2.2 性能评估
考虑细小裂缝、复杂背景、污渍污染和光照不均匀等情况,本文算法、文献[7]、[8]和[10]算法的部分实验结果分别如图7的3~6列所示,图7中第1列为原图像,第2列为手动标注结果。其他3种算法无法检测特别细的裂缝,在图像背景干扰较多时,无法滤除干扰目标,且分割裂缝的连续性较差,而本文算法能完整检测细小裂缝,且降低复杂背景及不均匀光照干扰,保留裂缝区域。

图7 4种算法实验结果Fig.7 Results of four methods
分别统计4种算法的性能指标平均值如表2所示,本文算法的精确率、召回率和综合评价指标F值均大幅度领先于其余3种算法,F值分别提升115%、148%和238%。在单线程运行速度上,本文算法处理每张图像的平均耗时仅为1.73 s,接近文献[10]算法,远快于文献[7]和文献[8]算法。
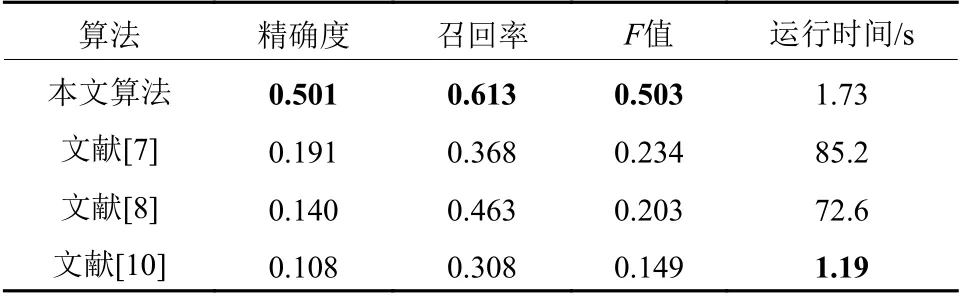
表2 4种算法的性能指标值Table 2 Experimental performance of four methods
3 结论
本文提出一种嵌入式平台上高分辨率裂缝图像的实时检测算法,所建立的裂缝聚合模型在一定程度上模拟了裂缝的延伸趋势,仅将延伸趋势一致的连通域聚合,抑制了大量灰度表现与裂缝相似的背景干扰。对比实验表明,本文算法大幅度领先于数种现有算法,有效提高了桥梁裂缝检测算法的可靠性和实时性,可应用于嵌入式平台上实时检测桥梁裂缝。但本文算法仅处理灰度图像,对彩色线状干扰的抑制能力不足,后期考虑引入彩色信息,进一步提高算法的可靠性。

