下肢外骨骼机器人动力学参数辨识与步态跟踪
刘 洋,彭世国,马宏志,廖维新
(1. 广东工业大学 自动化学院, 广东 广州 510006;2. 香港中文大学 机械与自动化系, 香港 999077)
人口老年化、交通意外和脑中风导致越来越多的人出现下肢运动功能障碍。下肢外骨骼机器人(Lower Limb Exoskeleton Robot, LLER) 能够帮助下肢伤残、偏瘫、有运动功能障碍的患者和身体虚弱的老年人进行康复训练和助力行走。因此,备受业内专家学者和健康医疗机构关注[1-2]。刚出台的《“十四五”机器人产业发展规划》和《“十四五”医疗装备产业发展规划》对于外骨骼机器人相关技术的研究给予高度重视和大力支持。下肢外骨骼机器人是一个多变量、强耦合的非线性系统,为了使其动作更协调柔顺、步态更自然平稳、轨迹更平滑精准,建立人机协同系统精确的动力学模型和参数辨识是首要和关键步骤[3-4]。目前,国内外学者提出的机器人参数辨识方法有:(1) 解体测量计算法[5]:无需运动数据采集和算法设计,但不易精确测量质心位置,且拆解后无法考虑关节摩擦力的影响。(2) CAD辅助法[6]:惯性参数由软件或理论公式自动计算得到的理想值,但在实际加工及装配过程中会产生误差。(3) 线性化整体辨识法[7-8]:先对动力学模型进行线性化处理,得到线性回归矩阵和惯性参数矩阵,再驱动机器人运动,一次性辨识出所有参数,但计算量较大,存在重复辨识和误差累积等问题。(4) 多次辨识法[9]:对整体辨识法加以改进,将机器人按关节分组后进行多次驱动和参数辨识,但忽略了关节摩擦的影响。王靖森等[10]和席万强等[11]考虑摩擦,对六自由度机器人进行建模和辨识,提高了模型精度。(5) 内部传感器法:采用编码器测量关节角度,根据驱动器电流计算转矩,但转矩常数随着温度和寿命而变化存在误差。耿令波[12]采用测驱动电流和关节力矩的综合辨识法,实现惯性参数和摩擦解耦。(6) 外部传感器法[13]:通过高精度视觉系统捕获运动数据,通过安装在基座的力传感器测力矩,但并不能得到所有的惯性参数,且机器人基座需要多次定位,位置坐标变换计算复杂。(7) 负载辨识法:陈友东等[14]仅驱动机器人的部分关节减少关节耦合误差,运行激励轨迹,在负载变化时进行动力学参数辨识。陈柏等[15]通过优化激励轨迹对六自由度工业机器人负载动力学模型进行辨识,再补偿已知机器人本体参数模型,得到本体和负载结合的动力学模型。
针对下肢外骨骼机器人人机协同系统,本文借鉴上述工业机器人的参数辨识方法,并进行综合与改进,提出一种将外骨骼参数辨识实验方法与人体下肢参数计算方法相结合的动力学参数辨识方案。首先,为了考虑摩擦力对参数辨识的影响,在文献[16]建立的二连杆结构机器人动力学模型中加入摩擦力项,得到转矩表达式和一组待辨识的最小惯性参数。其次,提出一种静态与动态结合的实验辨识方法:先多次驱动单个关节,使大腿和小腿分别运动到不同位置后保持静止,使转矩表达式中的角速度项和角加速度项变为零,计算更简单;再以最简单的正弦函数作为最优激励轨迹驱动下肢连续摆动;并利用MATLAB进行在线数据采集、计算和曲线绘制,依据曲线特征和最小二乘法完成外骨骼参数辨识。再次,选取余弦函数作为激励轨迹进行参数辨识结果验证。然后,依据人体生理特征对下肢参数开展近似计算,并综合实验辨识结果建立人机协同系统精确的动力学模型。最后,采用基于模型上界的滑模控制,并引入低通滤波器开展步态轨迹跟踪研究。
1 动力学模型
笔者课题组研制了一款如图1(a~b) 所示的下肢外骨骼服[16]。当使用者穿戴下肢外骨骼服,单腿支撑且另一条腿摆动行走时,为了便于分析和计算,将脚和小腿作为一个整体,下肢的摆动近似简化为二连杆在矢状面XOY内的运动,如图1(c) 所示。以摆动腿的髋关节O为坐标原点,大腿绕其转动,OA长度为L1,质量为m1, 质心C1距 离O点l1,与竖直方向的夹角为θ1,θ1∈[−30◦,120◦]。小腿绕膝关节A转动,长度为L2,质量为m2, 质心C2距离A点l2,与大腿延长线方向的夹角为θ2,θ2∈[−120◦,0◦]。大腿绕通过髋关节O并垂直于XOY平面的Z轴转动的转动惯量为I1,小腿绕通过膝关节A并平行于Z轴转动的转动惯量为I2。
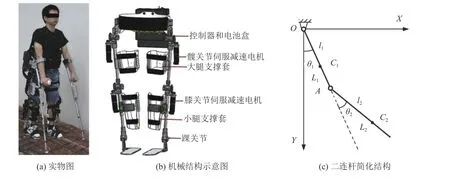
图1 下肢外骨骼机器人及二连杆结构Fig.1 The diagram of LLER and two links structure
一般,一个关节机器人的动态性能可由如式(1)二阶非线性微分方程描述[17]。
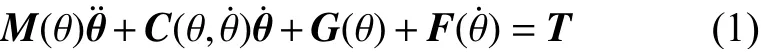
式中:θ ,θ˙,θ¨ ∈Rn×1分别为关节的角位置、角速度和角加速度,M(θ)∈Rn×n为机器人的正定惯性矩阵,C(θ,θ˙)∈Rn×1为 离心力和哥氏力矩阵,G(θ)∈Rn×1为重力项,F(θ˙)∈Rn×1为摩擦力项,若只考虑黏滞摩擦和库仑摩擦,F(θ˙)=fvθ˙+fcsgn(θ˙),fv∈Rn×n为黏滞摩擦系数矩阵,fc∈Rn×n为库伦摩擦系数矩阵,T∈Rn×1为关节驱动力矩。重力加速度g取9.8 m/s2。
因此,二连杆结构的机器人动力学方程为

式 (3) 中,共有12个未知参数,为了计算简便,重新定义5个新参数作为一组动力学最小惯性参数:
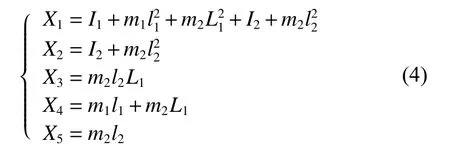
则,式(2) 可以写成
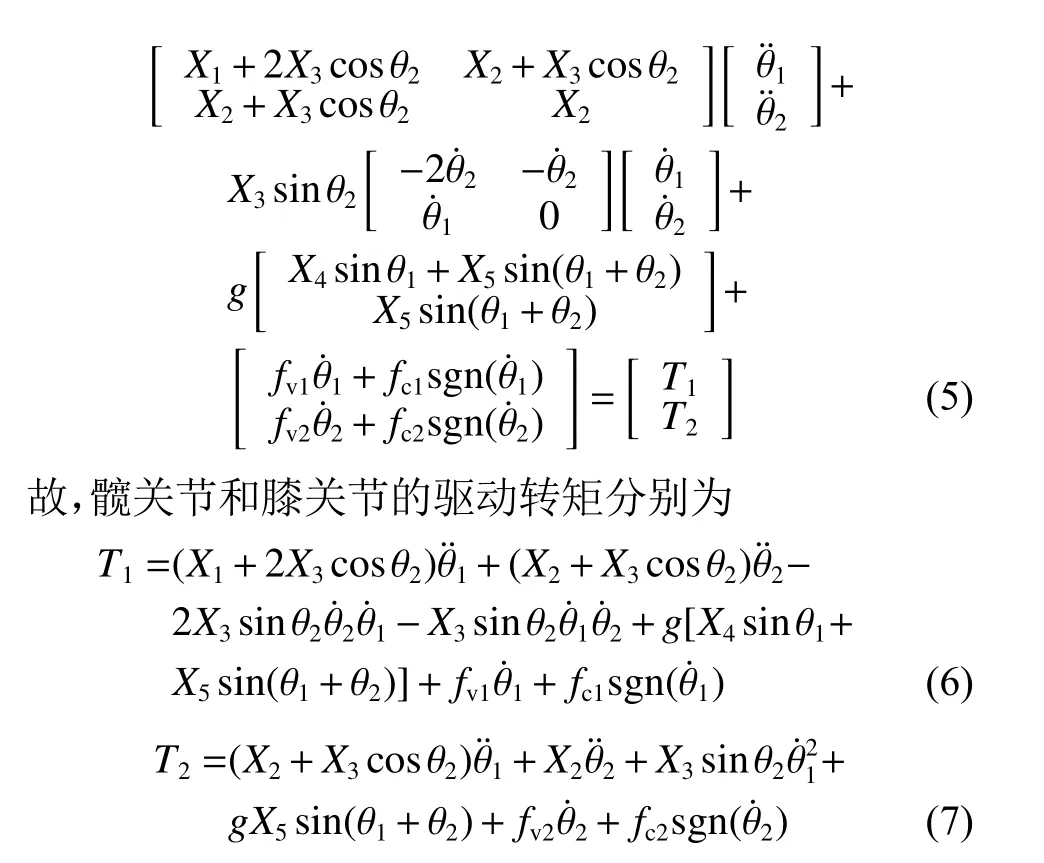
如图1(b) 所示,安装在关节处的成套减速电机(包括编码器、直流伺服电机和行星减速齿轮)较重,且足部踏板质量不可忽略,导致各连杆的质心不在几何中心位置,即式(3) 中的l1和l2难以准确描述。同时即使已知各连杆的质量,而I1和I2也未知,且摩擦力项F(θ˙)无法通过传感器检测。显然,仅通过测量与计算无法建立精确的系统模型。因此,进行系统动力学参数辨识十分必要。
2 参数辨识实验
2.1 实验方案及准备
机器人动力学参数辨识是一个复杂的系统工程,包括动力学建模、激励轨迹的选取、实验设计、数据采集与处理、参数估计、模型验证等环节[12,19]。本文动力学参数辨识与实验验证方案如图2所示。其中,X表示外骨骼动力学最小惯性参数集,Xload表示人体下肢动力学最小惯性参数集,T表示采用滑模控制输出的关节驱动转矩,T'表示经过低通滤波后输出的关节驱动转矩。e,e˙,e¨表示关节角度跟踪误差及误差一阶和二阶导数。
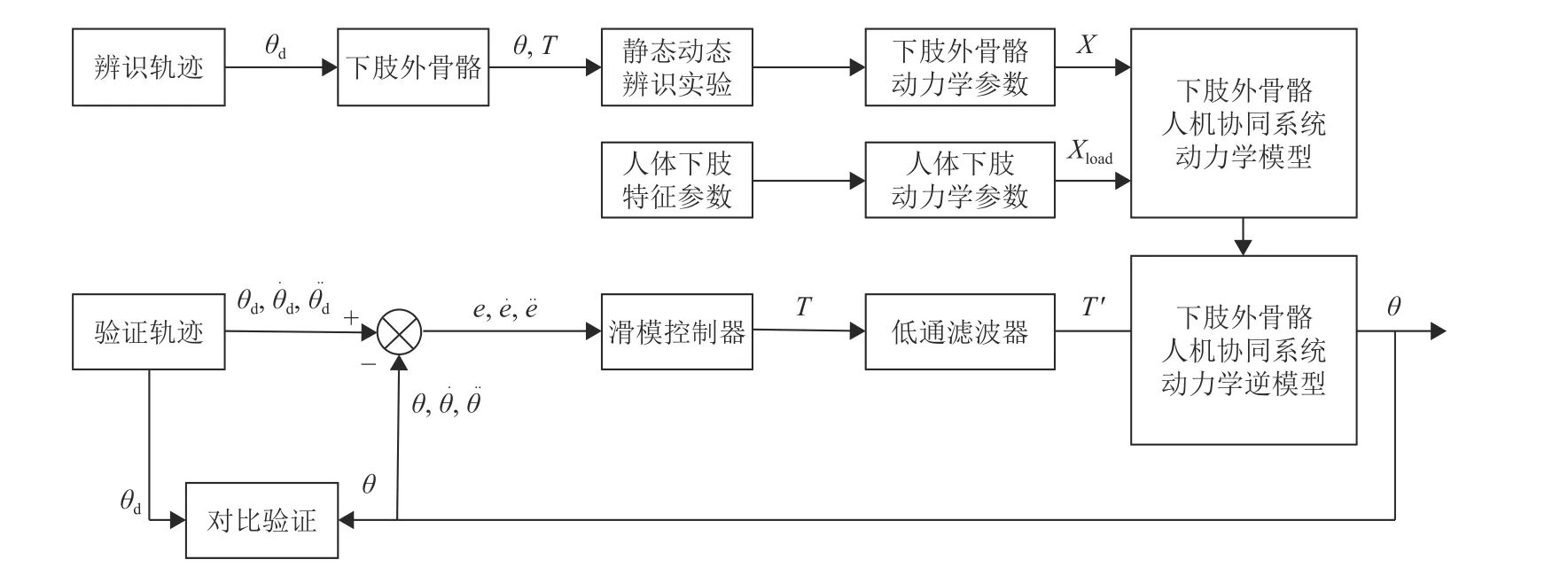
图2 动力学参数辨识方案设计Fig.2 The design of dynamic parameter identification of LEER
如图3所示,实验前用绳子将外骨骼悬空吊起,用支架将其固定,使其躯干与双腿都处于竖直静止状态。控制右腿髋关节和膝关节处的电机来驱动大腿和小腿(含足部) 运动,模拟外骨骼左腿竖直支撑且右腿摆动行走的过程。

图3 LLER参数辨识实验过程Fig.3 The process of LLER parameter identification
2.2 静态实验
对于髋关节和膝关节,定义关节离开初始位置为反向运动,返回初始位置为正向运动。轮流让其中一个关节在初始位置固定不动,另一个关节运动到不同位姿后保持静止,此刻角速度和角加速度都为零,转矩表达式中仅剩重力项和摩擦力项,易于参数辨识。
图4所示为关节转矩与角度的关系。
第1步:让右腿竖直且膝关节保持静止, θ2=0◦,髋关节初始角度 θ10=0◦。由上位机给电机控制器发送髋关节角度期望信号θ1d0=30◦,控制器在简单比例控制作用下输出控制电压u1=kp1(θ1d0−θ10)驱动右大腿摆动到 30◦位置后停止,记录该位置的关节驱动转矩T10。 每次将θ1di增 加2◦, 直到θ1d30=90◦为止,记录此刻关节处驱动转矩T130, 得到θ1反向增加时髋关节驱动转矩曲线T1−

i,如图4(a) 所示。


第4步:由上位机给电机控制器发送膝关节角度期望信号 θ2d31=−68◦,电机驱动右小腿反向摆动到−68◦位 置后停止,记录此刻关节处驱动转矩T231。依次将 θ2di增 加2◦, 直到θ2d60=−10◦,记录此刻关节处驱动转矩T260, 得到θ2正向增加时膝关节驱动转矩T2+i曲线,如图4(b) 所示。

根据式(16) ,结合实验测得的60组数据,求均值得到fc2=−1.521。根据式(17) ,结合实验测得的60组数据,求均值得到X5=0.513。根据式(12) ,结合实验测得的60组数据,求均值得到X4=1.871。已知外骨骼大腿的长度L1=0.5, 由式(4) 得X3=X5L1,计算得出X3=0.257。
2.3 动态实验
对于髋关节和膝关节,轮流让其中一个关节在初始位置固定不动,另一个关节先匀速运动使其角加速度为零,绘制摩擦曲线可求黏滞摩擦系数。再通过正弦函数激励轨迹让关节周期性摆动求转动惯量参数。
第1步:让右侧小腿与大腿保持直线,即膝关节不运动,θ2=0 ,θ ˙2=0 ,θ ¨2=0。由上位机给电机控制器发送髋关节角度期望信号θ1d(t)=kt,通过简单比例控制算法使得电机驱动大腿带动小腿和足部一起摆动。髋关节匀速运动,θ˙1=k∈[−25,25], θ ¨1=0。根据式(6) 得,
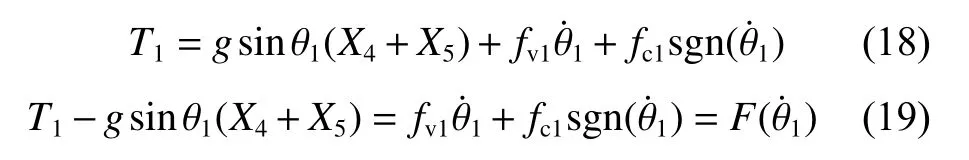
式中:T1、X4、X5、fc1均 为已知,计算并绘制F(θ˙1)如图5(a) 所示。根据黏滞摩擦和库伦摩擦特性,将图5(a) 中实测数据拟合成黑色折线,利用最小二乘法进行估计得到fv1=−0.062, 扰动f1=−1.796。
第2步:让右侧大腿重新保持竖直和静止,即髋关节不运动,θ1=0 ,θ ˙1=0 ,θ ¨1=0。由上位机给电机控制器发送膝关节角度期望信号 θ2d(t)=kt,通过简单比例控制算法使得电机驱动小腿带动足部一起摆动。膝关节匀速运动,θ ˙2=k∈[−25,25], θ¨2=0。
根据式(7) 得,
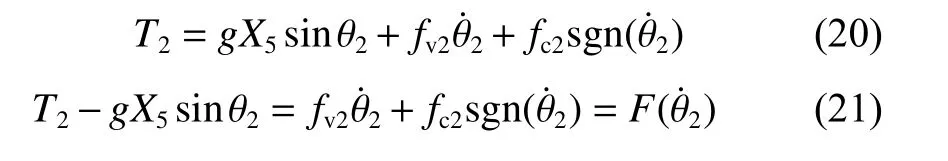
式中:T2、X5、fc2均 为已知,计算并绘制F(θ˙2)如图5(b)所示。根据黏滞摩擦和库伦摩擦特性,将图5(b) 中实测数据拟合成黑色折线,利用最小二乘法进行估计得到fv2=−0.503。
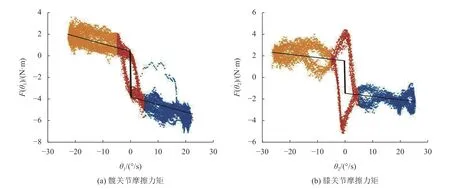
图5 关节摩擦力矩F (θ˙)曲线Fig.5 The curves of joint friction torque
第3步:让右侧大腿重新保持竖直和静止,即髋关节不运动 θ1=0 ,θ ˙1=0 ,θ ¨1=0。膝关节激励轨迹选取:θ2d(t)=−30◦+20◦sin(2πft),通过简单比例控制算法使得电机驱动小腿和足部一起摆动。其中f为0.2 Hz,以频率100 Hz采集T2和 θ2,计算出每个采样点的角速度θ ˙2和角加速度θ ¨2。
根据式(7) 得,

式中:T1、X3、X4、X5、fc1、fv1均为已知,利用最小二乘法辨识可得X1=9.506。
综上所述,参数辨识结果如表1所示。
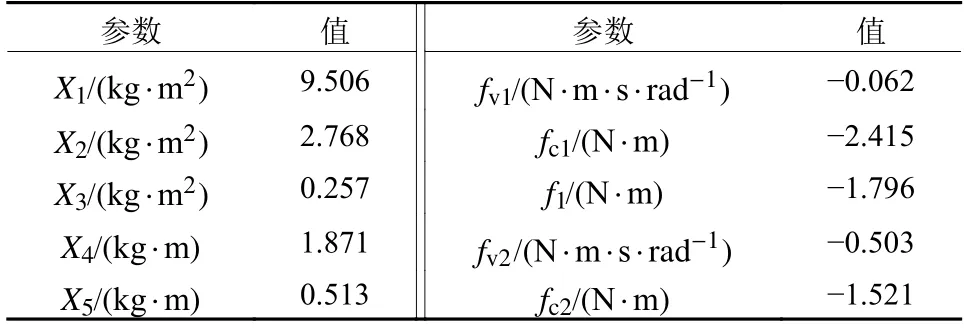
表1 参数辨识结果Table 1 The results of parameter indentification
2.4 辨识结果验证
根据髋关节和膝关节实际角度的变化范围:θ1∈[−30◦,120◦],θ2∈[−120◦,0◦],选取验证激励轨迹:
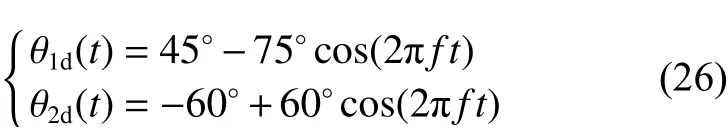
式中,f=1 Hz。将式(26) 与参数辨识结果代入式(6~7) 计算,并绘制曲线。在式(26) 激励轨迹驱动下,外骨骼髋、膝关节同时运动,根据电机驱动器电流和已知的转矩系数,计算得到关节驱动转矩实际值,并绘制曲线。如图6所示,将转矩计算值与实际测量值进行对比分析发现,关节转矩计算值(红色曲线)都比实际测量值(蓝色曲线)略小,原因在于实际系统运行时,存在外部扰动转矩,而动力学模型对此忽略不计。在一定误差范围内,二者波形基本一致,表明外骨骼参数辨识结果正确。
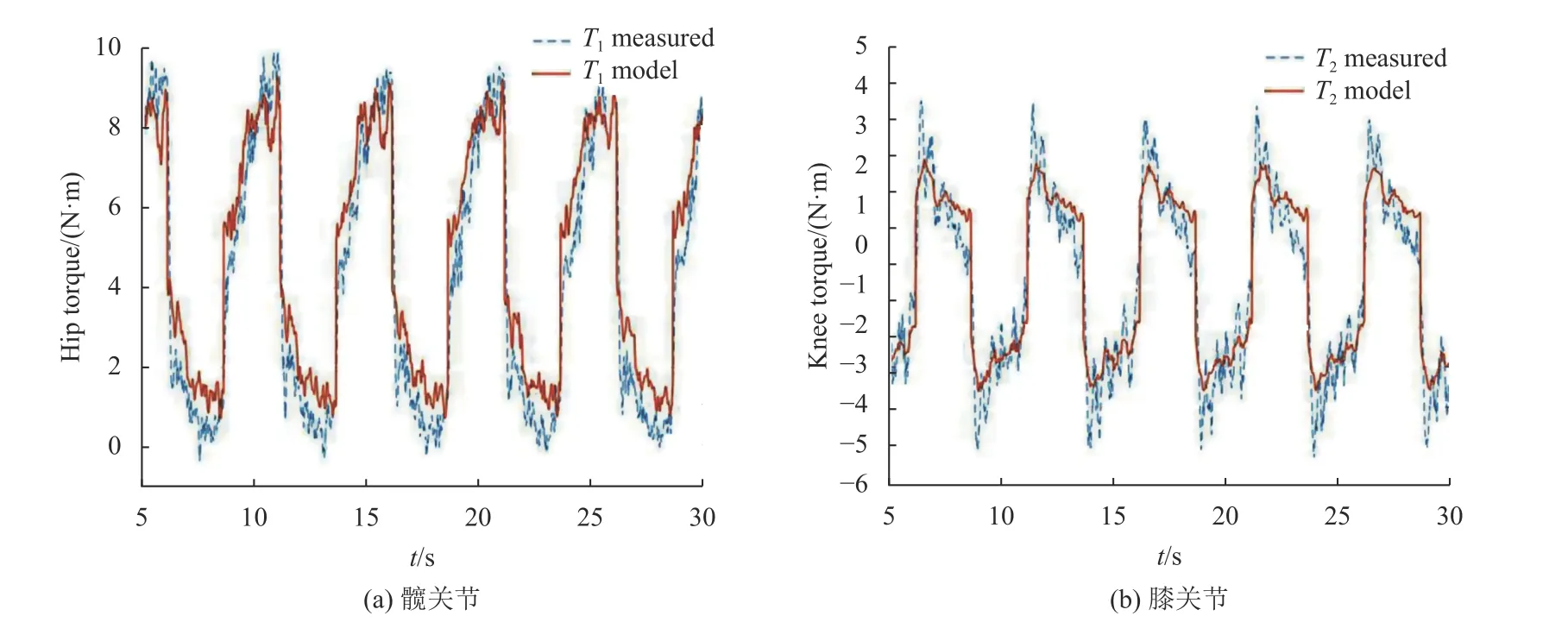
图6 关节转矩实际值与计算值Fig.6 The tested and calculated values of joint torque
3 步态跟踪滑模控制
3.1 人机协同系统模型
在本项目中[16,20],外骨骼服的质量m0=20 kg,穿戴者身高168 cm,与外骨骼服尺寸完全相符合,L1=0.5 m,L2=0.38 m ,体重mload=70 kg,根据成年人各部分肢体长度与身高的比例关系和各部分肢体质量与体重的关系来确定人体下肢的几何参数及惯性参数[21]。大腿的质量为
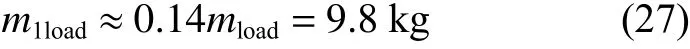
小腿与足部的总质量为
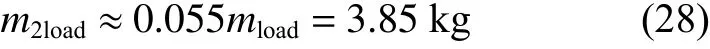
由于人体肌肉组织分布比较均匀,为了计算简便,将大腿和小腿(含足部)的质心都取在几何中心位置,则有

3.2 基于模型上界的滑模控制
滑模控制(Sliding mode control, SMC)具有响应快、对参数变化和扰动不灵敏、鲁棒性强等特点,但其不连续的开关特性会引起系统高频抖振。
由机器人系统动力学特性可知[17]:存在一个线性回归矩阵 Φ(θ,θ˙,θ˙r,θ¨r)∈R2×3和依赖于机器人质量特性的惯性参数向量p∈R3×1,使得机器人系统动力学模型式(1)满足式(34)的线性关系:

下肢外骨骼机器人在单腿支撑且另一条腿摆动过程中,髋关节和膝关节实际角度θ =[ θ1θ2]T,期望角度θd=[ θ1dθ2d]T, 误差e=θd−θ。Λ 为一个二阶正对角矩阵,定义参考角速度 θ ˙r= θ˙d+Λe,则参考角加速度θ ¨r= θ¨d+Λe˙,取滑模面的切换函数为

3.3 稳定性分析

3.4 仿真结果及分析

图7表明,采用滑模控制的外骨骼人机协同系统,除了角速度存在抖动外,步态轨迹跟踪效果良好。在零时刻,髋关节期望初始位置 θ1d(0)=−30◦,膝关节期望初始位置 θ2d(0)=0◦,而外骨骼双腿竖直向下,髋关节实际初始位置θ1(0)=0◦,膝关节实际初始位置 θ2(0)=0◦。系统起动后,外骨骼膝关节立刻就能完全跟随期望轨迹变化;而髋关节在约0.15 s内先反向摆动微小角度再立刻正向摆回初始位置,直到θ1d(0)=0◦时,髋关节才会完全跟随期望轨迹变化。在实际过程中,因存在惯性,髋关节电机产生瞬时微弱震动。
如图8(a) 所示,滑模控制器输出转矩具有较大的抖振。在滑模控制器串联一阶低通滤波器后,转矩抖振大幅度减小,如图8(b) 所示。表明低通滤波器能够有效地抑制或减小滑模控制引起的抖振。
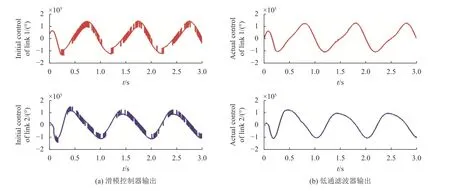
图8 滑模控制低通滤波前后输出转矩对比Fig.8 The comparison of output torque before and after SMC low-pass filtering
4 结论与展望
本文先对外骨骼开展参数辨识实验,再对人体下肢进行惯性参数计算,最后综合得到二连杆结构的人机协同系统精确的动力学模型。基于模型上界的滑模控制能实现步态轨迹精准跟踪,低通滤波器能有效减小滑模控制引起的高频抖振。这为下肢外骨骼动力学参数辨识提供了一种解决方案,为基于模型的控制方法提供了一种参考模型,也为下肢外骨骼人机协同系统的步态轨迹精准跟踪控制提供了一种参考方法。
将下肢外骨骼近似简化为二连杆结构,模型更简单,待辨识参数更少。在静态与动态结合的实验辨识过程中,利用MATLAB在线采集电机驱动器的电流和重新标定后的转矩系数来实时计算驱动转矩,减小误差,也无需在关节内安装力矩传感器,元件更少,结构更简单,结果更精确。与通常采用的求线性化回归矩阵的参数辨识方法相比,不仅待辨识参数更少,而且实现了惯性参数和摩擦力解耦,还避免了对回归矩阵求逆。但人体下肢惯性参数近似计算可能引起模型参数误差。可安装人机交互力传感器构成反馈环节,通过人工智能算法对模型参数进行自动调整,使物理模型与参数模型的高精度一致。引入一阶低通滤波器减小滑模控制引起的抖振,方法简单有效。还可通过改进滑模控制律或者人工智能算法来减小抖振。另外,外骨骼机器人助力行走的步态规划问题值得进一步研究。

