方钢管超高性能混凝土界面黏结滑移性能

王秋维，梁林，史庆轩，王朋

［1.西安建筑科技大学土木工程学院，陕西西安 710055；2.西部绿色建筑国家重点实验室（西安建筑科技大学），陕西西安 710055；3.结构工程与抗震教育部重点实验室（西安建筑科技大学），陕西西安 710055］

超高性能混凝土（UHPC）具有超高强度、高韧性和优异的耐用性，是一种节能、低碳的新型水泥基复合材料，在公路、桥梁和建筑等工程中被广泛应用［1-2］.然而，无纤维或低纤维掺量的UHPC 具有较大的脆性，限制了其作为承重构件在结构中大量应用.为改善UHPC 的脆性，将其灌入钢管形成钢管UHPC组合结构，依靠钢管的约束作用可改善其脆性，同时两者结合可明显提高钢管UHPC 构件的承载、变形和耗能能力并降低其建设成本，具有广阔的应用前景［3-4］.

钢管UHPC 的界面黏结作用是两者共同受力、协同变形的重要前提，研究表明考虑界面黏结作用的钢管高强混凝土承载能力明显提升（约15%），且混凝土强度越高提升越显著［5］.但若界面黏结强度不足，钢管与UHPC 会发生相对滑移，导致钢管UHPC构件产生应力重分布，进而会影响其承载性能.目前，相关研究主要集中在钢管普通混凝土的黏结滑移性能，涉及黏结滑移机理、黏结强度计算等，如：Qu等［6］通过钢管混凝土的荷载推出试验，分析了界面的黏结滑移特性和润滑油对黏结强度的影响，给出临界剪应力传递长度建议值；Tao 等［7］对不同类型钢管混凝土进行了单调推出试验，发现不锈钢钢管混凝土的黏结强度低于碳素钢钢管混凝土，提出可通过设置焊环和采用膨胀混凝土提高黏结强度；任庆英等［8］对内壁设置栓钉的钢管混凝土大尺寸试件进行推出试验，提出了考虑界面黏结的柱受剪承载力计算方法；Feng 等［9］通过空心钢管混凝土的单轴推出试验，发现除高宽比和宽厚比外，混凝土强度也对界面黏结强度有一定影响.

然而，UHPC 去除粗骨料，采用细骨料和微细胶凝材料使内部颗粒形成最紧密堆积结构并掺入钢纤维增强基体，其孔隙率小、孔隙分布均匀、密实度高，与普通混凝土有较大差别［10-11］.因此，钢管UHPC 的界面黏结滑移性能明显区别于钢管普通混凝土，而这方面的研究较少.针对此问题，作者课题组已对圆钢管UHPC 的黏结滑移机理和参数影响进行了研究［12-13］，与圆钢管相比，方钢管虽对核心混凝土的约束作用较弱，但方钢管UHPC 构件仍具有承载能力高、截面惯性矩大、延性和耗能能力良好、节点连接简单和易施工等优点，在高层和大跨结构中被广泛应用［14］，而对方钢管UHPC 界面黏结滑移性能的研究尚较少.本文在前期研究基础上，设计了18 个方钢管UHPC 推出试件并对其进行静力推出试验，分析了钢管宽厚比、高宽比和UHPC 抗压强度等对试件黏结滑移性能的影响，建立了不同养护条件下的方钢管UHPC 黏结强度计算模型，研究结论可为方钢管UHPC构件在工程中的设计与应用提供依据.

1 试验概况

1.1 试件设计与制作

试验共设计并制作了18个方钢管UHPC 推出试件，主要设计参数为钢管宽厚比、高宽比和UHPC 抗压强度.方钢管采用含碳量0.2%、抗拉强度为245～410 MPa钢材通过冷弯焊接成型制作［15］，其截面宽度b均为150 mm，厚度t包括3.5 mm、6 mm 和8 mm 三种，对应宽厚比b/t分别为42.86、25.00 和18.75；试件高度l分为350 mm 和480 mm 两种，相应的高宽比l/b分别为2.33 和3.20.UHPC 立方体抗压强度设计值fcu分别为160 MPa、140 MPa 和120 MPa.试件具体设计参数如表1 所示，其中，含钢率α为钢管与UHPC 截面面积之比，α越大表明钢管对UHPC 的约束作用越强［14］；编号规则为：A、B、C表示UHPC的3种配合比，3.5、6 和8 表示钢管厚度分别为3.5 mm、6 mm 和8 mm，1和2表示试件高度分别为350 mm和480 mm.

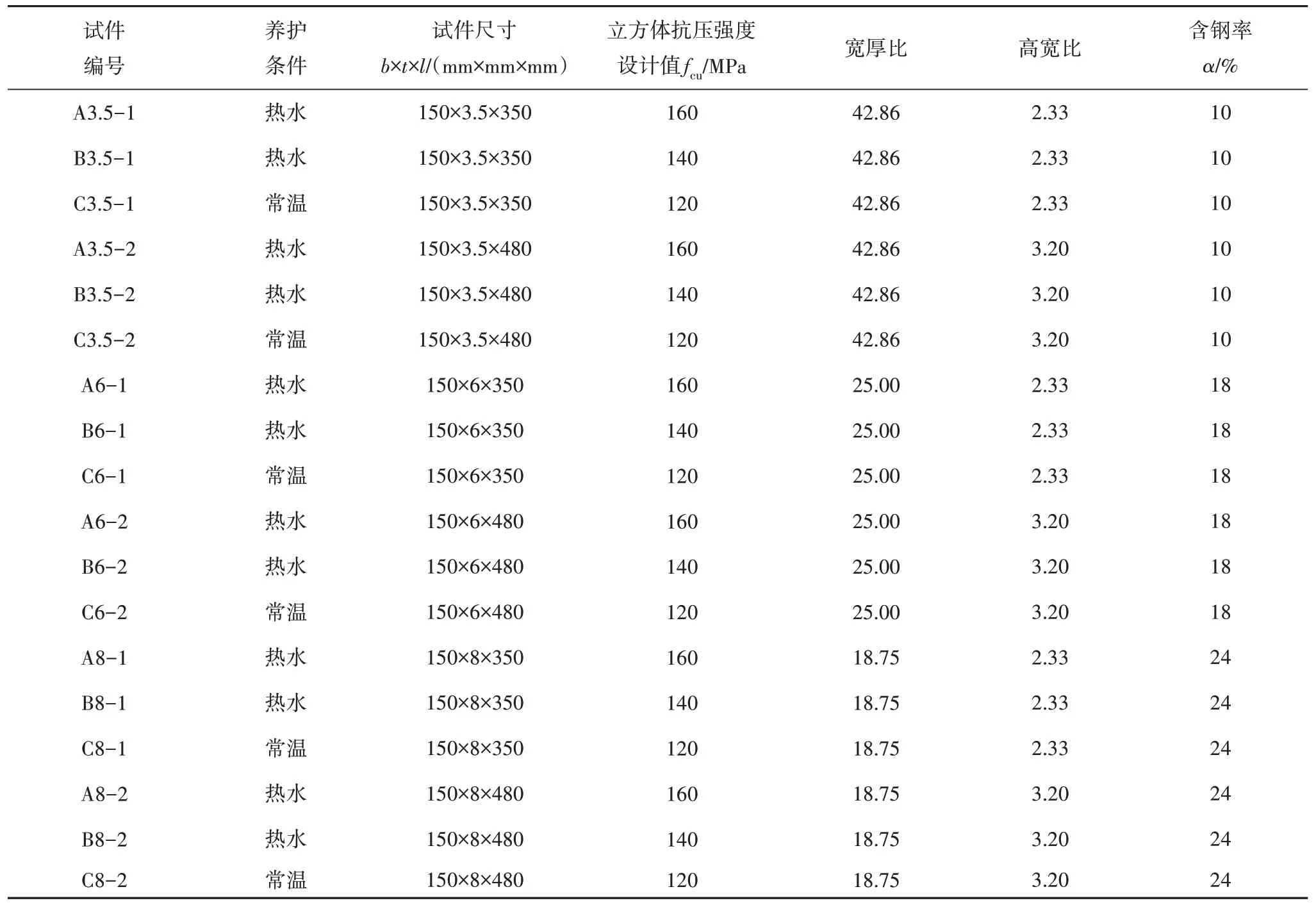
表1 试件主要设计参数Tab.1 The main design parameters of specimens

UHPC 的原材料包括P42.5 普通硅酸盐水泥、硅灰、石英粉、级配石英砂（粗砂、中砂和细砂）、钢纤维、消泡剂、减水剂和水，其中，钢纤维采用长直镀铜钢纤维，密度为7.8 g/cm3，直径为（0.20±0.03）mm，长度为（13.0±1.3）mm；减水剂属于聚羧酸类，减水率≥30%；消泡剂采用改性聚硅酮类，pH 值为8.0±0.5，密度为（1.10±0.05）g/cm3.基于最紧密堆积原则，通过将UHPC 内部缺陷降到最低，并分别采用常温和90 ℃热水两种养护方式，以此获得3 种试件设计强度的配合比方案，具体见表2，其中钢纤维体积掺量为1.72%和1.28%，属于低掺量（小于2%）钢纤维.

表2 UHPC配合比Tab.2 The mix proportion of UHPC

试件制作时，首先用云母板和胶着剂封闭钢管底部，将搅拌好的UHPC 灌入钢管中，当浇筑面距钢管顶端50 mm 时，置于振动台充分振捣密实.为防止漏浆和钢管振捣时倾倒，采用木支架固定试件，浇筑完毕后对试件进行编号并分类养护.试件养护制度分为两类：1）采用塑料膜包裹试件两端，并置于常温（20±5）°C 下养护28 d；2）将试件浸泡在90 °C 恒温水箱中养护3 d，然后取出置于常温环境养护，为防止热水养护下钢管表面出现锈蚀，待试件取出后对其依次进行干燥、机械打磨和涂刷除锈剂.

1.2 材料力学性能

按照GB/T 31387—2015 的规定［16］，采用尺寸为100 mm×100 mm×100 mm 立方体试块和100 mm×100 mm×300 mm 棱柱体试块进行材料力学性能测试，试块分为A、B、C 3组，每组3个试块.材性与对应钢管UHPC 试件的养护条件一致.采用TYA-2000 型电液式压力试验机进行加载，将试块的两个平整面放置于压力机上下加载板的中心，并进行对中，加载速率为1.2～1.4 MPa/s，当荷载增长速率为负值时停止加载.在3 种配合比下，UHPC 的实测立方体和棱柱体抗压强度平均值，如表3 所示.可见，UHPC 实测立方体抗压强度稍低于设计值（5 MPa以内），满足材料强度设计要求.钢材按照GB/T 228.1—2010［17］留取材性样品，采用电子万能试验机和电子引伸计测定了3 种厚度钢材的屈服强度fy、极限强度fu和弹性模量Es，如表4所示.

表3 UHPC力学性能Tab.3 Mechanical properties of UHPC

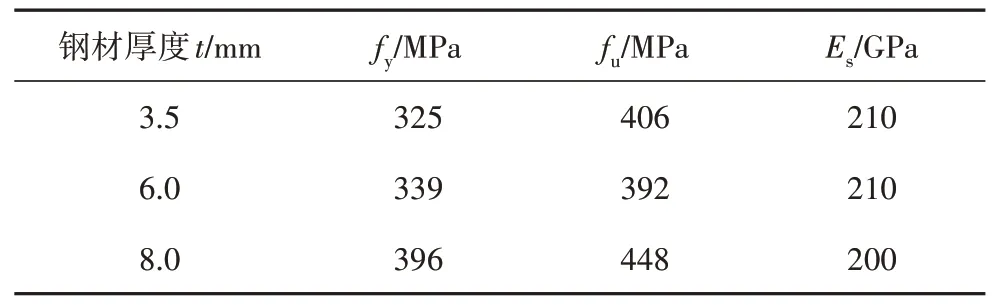
表4 钢材力学性能Tab.4 Mechanical properties of steel

1.3 加载装置及量测内容

试件在WAW1000电液伺服试验机上进行加载，通过TDS-602 静态数据采集仪记录试验数据，将试件预留空隙端朝下放在下加载板上，在试件上部与上加载板之间放置一个方形钢垫板，钢垫板截面比试件截面略小，加载压力由上端推向下端，将有方形垫块的一端称为加载端，空钢管端称为自由端.试件加载时，先施加预压力1～5 kN，使试验机上下加载板、钢垫板、试件之间挤压密实，之后保持加载速率为0.4 mm/min，当荷载-滑移曲线较为平滑或者加载端滑移量达到40 mm 时停止加载.试验加载装置如图1所示.

图1 加载装置Fig.1 Test setup

试验主要量测内容包括黏结荷载、界面滑移和钢管应变.黏结荷载通过荷载传感器获得，在加载端和自由端各布置两个对称的位移计以测量界面相对滑移，加载端的位移计通过磁性表座固定在横梁上，自由端的位移计下部与钢棒连接，钢棒则垫在自由端内部放置的木块下方，由此便可实现位移计与内部UHPC 的同步滑移，如图2（a）所示.钢管应变由布置在钢管表面的应变片测得，应变片沿试件高度各布置5层（l=350 mm）和6层（l=480 mm），每层纵向和横向应变片各2个，如图2（b）所示.

图2 测点布置Fig.2 Measurement points arrangement

2 破坏过程与形态

加载初期，加载端及自由端即开始产生局部滑移；随着荷载增加，滑移区域逐渐向试件中部延伸，可听见“嗒嗒”的声音，滑移区域的化学胶结力丧失，摩擦力及机械咬合力发挥作用；荷载继续增大，中部区域开始滑移，大部分界面处于滑移状态，当达到极限状态时，方钢管与UHPC 界面产生整体滑移，所有试件均在较小滑移时产生黏结破坏.试验结束后，试件整体较为完整，钢管无鼓曲，但可在加载端看到混凝土与钢管摩擦留下的痕迹，钢管内边缘处混凝土有较为明显的损伤.推出后试件整体如图3 所示，其中上部为加载端，下部为自由端.

图3 推出后试件Fig.3 Specimens after push-out test

对每种厚度的钢管各取3 个典型试件，从俯视角度观察加载端破坏形态，如图4 所示，其中白线上方为钢管内部擦痕较明显的部位，下方为无擦痕部位.分析可知，不同宽厚比试件由于约束作用不同，钢管内擦痕也呈现不同特点，宽厚比较大（t=3.5 mm）时，擦痕主要集中于界面角部，较小时（t=6 mm和t=8 mm）则向截面中部移动，可见宽厚比越小，钢管的约束作用越强，界面擦痕分布越趋于均匀.

图4 试件加载端破坏形态Fig.4 Failure patterns of loading ends of specimens

3 试验结果与分析

3.1 荷载-滑移曲线

在推出试验中，同步测试各试件的荷载和界面滑移量，得到相应的荷载（P）-滑移（S）曲线，如图5所示，其中实线和虚线分别为加载端和自由端的滑移曲线.由图5可知：

图5 试件荷载-滑移曲线Fig.5 Load-slip curves of specimens

1）加载初期，曲线处于上升阶段，界面滑移量比荷载增加速度慢，且混凝土加载端的滑移量稍大于自由端，这是由于核心混凝土在加载板的作用下，出现了弹性压缩变形从而产生滑移，加载端的滑移最先出现、增长较快，随着黏结应力的传递，自由端的相对滑移才逐渐增大.

2）荷载进一步增加，加载端与自由端的滑移量接近，两者的P-S曲线逐渐重合，当宽厚比较大时，曲线有较明显的峰值点，峰值点之后曲线开始下降，如试件A3.5-1、A3.5-2、B3.5-2等；宽厚比较小时，曲线无明显峰值点，曲线趋于平稳或下降缓慢（如试件A6-1、B6-1 和B8-2），这是由于宽厚比越小，钢管对UHPC的约束作用越强，界面摩擦力和机械咬合力越大，从而试件的黏结破坏荷载较大，曲线会继续上升或下降较缓.其中，个别曲线在水平段出现先下降再上升的现象（如试件B8-1、B8-2），原因是黏结力在界面某处产生了突变，之后又回到原来状态，分析时不计入此种变化.

根据上述分析，可将钢管UHPC的P-S曲线归纳为两种类型，即软化型（曲线OAB）和强化型（曲线OAC），如图6 所示.由图6 可知，软化型曲线有较明显的峰值点，强化型曲线无明显的峰值点，当界面滑移量为6～8 mm 时（B和C点），两类曲线均趋于稳定.定义加载端滑移量Sl与自由端滑移量Sf的差为ΔS，则ΔS-Sl曲线斜率为零时的荷载为黏结破坏荷载Pu，原因为此时两端滑移增量基本一致，内部UHPC 产生整体滑移，认为试件达到黏结极限状态.

图6 典型荷载-滑移曲线Fig.6 Typical load-slip curves

图7 给出了两种类型典型试件（以B3.5-1 和A6-1 为例）的P-Sl曲线和ΔS-Sl曲线，P-Sl曲线的A点对应的荷载即为试件的黏结破坏荷载，即图6 中的A点，此点为软化型曲线的峰值点.当各试件达到Pu时，界面平均黏结滑移量约为1.77 mm，而同条件下圆钢管UHPC 的平均黏结滑移量约为1.0 mm［13］，表明方钢管与UHPC 的界面黏结性能略差，但相对于总滑移长度50 mm，其黏结滑移量较小（3.54%），两者仍具有较好的协同工作能力.

图7 试件ΔS-Sl曲线Fig.7 ΔS-Sl curves of specimens

3.2 黏结强度

在加载过程中，黏结应力沿界面长度的分布并不均匀，同一截面内中部与角部的应力也不尽相同，为了方便研究，常假设界面黏结应力为均匀分布.对于方钢管UHPC试件，其黏结应力可按下式计算：

式中：τ为界面平均黏结应力；A为界面面积.

黏结强度τu为发生黏结破坏时界面的剪应力，即Pu对应的黏结应力，计算所得各试件的τu如表5所示，其中Su为与Pu对应的滑移量.由表5可知：

表5 试件黏结强度Tab.5 The bond strength of specimens

1）其他条件相同时，随着钢管宽厚比减小，钢管的约束作用增强，这有效提高了机械咬合力和界面摩擦力，界面黏结荷载和强度因此而增大.

2）截面宽度不变时，增加高宽比即增加了试件高度，此时试件截面面积有所增大，从而黏结应力的传递速率减慢，τu整体呈减小趋势.

3）宽厚比较大（b/t=42.86）时，钢管的约束作用较弱，黏结强度主要受UHPC 强度影响，τu随着混凝土强度提升而增大.而宽厚比较小（b/t≤20）时，钢管约束作用较强，黏结强度受UHPC 强度和约束作用共同影响.此时τu随UHPC 强度增大呈现先增后减的趋势，原因为UHPC 强度越高，其自收缩特性越强［18］，约束作用在一定程度上被削弱.

3.3 纵向应变沿高度分布

图8 为不同级别荷载作用下，部分试件钢管外表面纵向应变（ɛv）沿高度方向的分布曲线，其中x为测点至加载端的距离.由图8可知，加载初期，ɛv沿钢管长度方向的变化并不明显，钢管与内部UHPC 界面能够均匀传力；随着荷载增加，沿管壁纵向的应变值出现较大差异，因试验过程中加载端仅混凝土受力，故可发现自由端应变明显大于加载端.同时，ɛv沿钢管纵向的应变差值变大，表明钢管与UHPC 之间的滑移随着荷载增加而变大，两者之间的协同工作逐渐被破坏.

图8 钢管表面纵向应变分布Fig.8 The longitudinal strain distribution on steel tube surface

对应变数据进行统计回归，发现钢管纵向应变沿高度方向大致呈指数分布，如图8 所示，钢管沿高度方向任意位置x的纵向应变εv（x）可表示为：

式中：A、B和k为钢管应变分布特征系数，每个试件不同荷载下的系数均不相同，具体由实测应变数据回归分析得到.采用式（2）回归得到的图8 中各拟合曲线的R2平均值为0.96，变异系数为0.04.

4 黏结强度计算

化学胶着力在加载初期发挥作用，对τu的影响较小［6］，计算中忽略化学胶着力，仅考虑界面摩擦力和机械咬合力的贡献，则τu的表达式为：

式中：τf和τw分别为黏结极限状态时的界面摩擦应力和机械咬合应力.

4.1 τf的确定

摩擦应力τf与界面内压力有关，可表示为：

式中：μ为界面摩擦系数；qu为与τu对应的界面内压力.

沿试件钢管高度方向取微元dx，如图9 所示，通常计算时假定界面内压力均匀分布［19］，根据平衡条件可得极限状态时qu和钢管环向应力σφu（x）的关系：

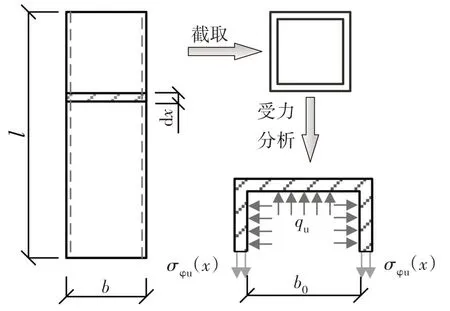
图9 qu和σφu（x）的关系Fig.9 The relationship between qu and σφu（x）

式中：b0为钢管内宽度.

对公式（5）的两边沿界面高度积分得：

式中：l0为界面高度，等于l减去钢管预留段的距离.

假设达到τu时，钢管中部环向应变沿高度方向的平均值为，分析试验数据，可得钢管环向应变沿高度方向的归一化分布曲线，如图10 所示.可见，归一化之后的环向应变分布较集中，且沿高度接近线性分布，建立曲线方程为：

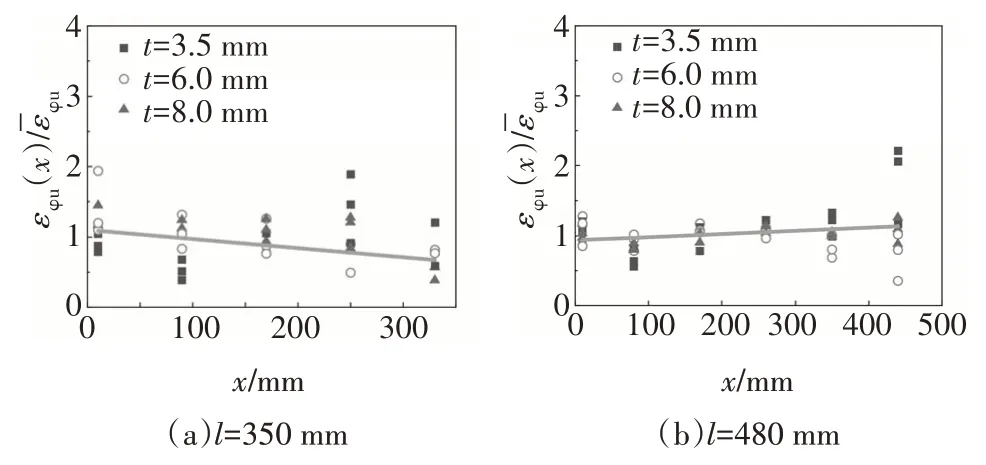
图10 钢管表面环向应变分布Fig.10 The transverse strain distribution on steel tube surface

式中：a和b为钢管环向应变沿高度的分布系数.

因试件在推出过程中，钢管基本处于弹性阶段，应力-应变关系符合胡克定律，故通过式（7）可得：

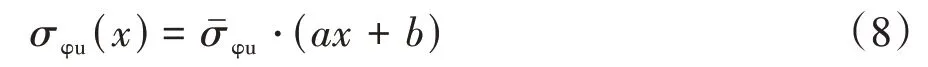
将式（8）代入式（6），计算得到：

式中：m和n为受钢管约束作用（a、b和γ）和界面摩擦特征（μ）影响的综合系数，m=aγμ，n=bγμ，具体取值在下文中通过数值拟合得到.

将式（10）中的b0和l0近似用b和l代替，则得：

4.2 τw的确定

化学胶结力失效后，钢管与混凝土界面上凸起颗粒挤压咬合形成机械咬合力，其咬合作用属于微观作用范畴.据统计，钢材表面粗糙偏差一般在微观量级上（10-2mm 左右），由这种微观偏差引起的界面作用力称为微观咬合力，如图11 所示［20］.当黏结滑移加速发展后，接触面上的混凝土微小凸峰便被剪切破碎，形成一层薄的滑动粉末层，机械咬合力随之丧失殆尽.影响机械咬合力的因素包括材料表面的粗糙程度、混凝土级配、混凝土抗剪强度、浇捣方式与方法、振捣器械的使用以及材料的受力方式，其中混凝土强度影响较大［21］.

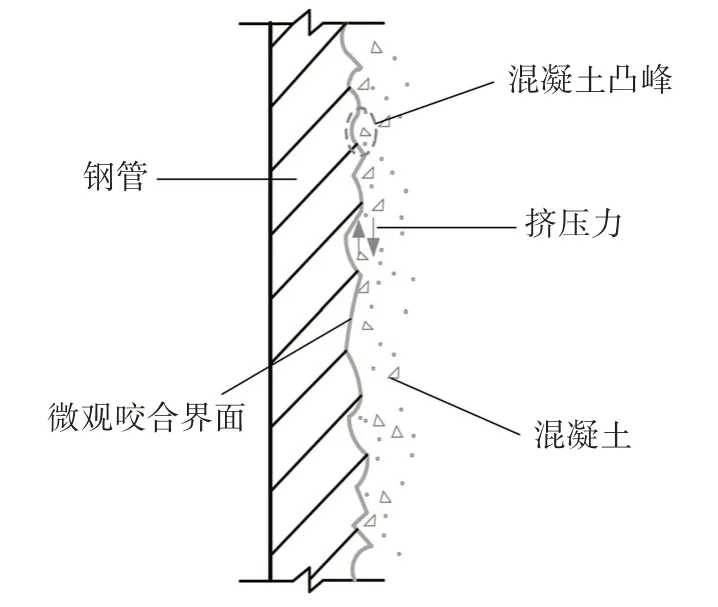
图11 微观咬合作用示意图Fig.11 Schematic of microscopic occlusion action

混凝土强度主要通过改变界面粗糙程度，从而影响黏结力（机械咬合力和摩擦力），文献［22］研究表明，（fcu）0.4的形式符合UHPC 强度对界面粗糙程度的影响趋势.因此，本文以同样形式考虑混凝土强度对界面机械咬合力的影响，并引入界面咬合影响系数c，建立公式（12）的机械咬合应力τw：

式中：c为界面咬合影响系数，其主要受材料表面的粗糙程度、混凝土级配、浇捣和振捣方式等影响.

4.3 模型建立及验证

将式（11）和式（12）代入式（3）得：

基于试验数据，采用数值分析软件1stopt对公式（13）进行拟合求解.由于不同养护条件下混凝土水化反应程度和生成物有所不同，造成的界面组成有所差异，故不同养护条件下系数m和n应有所区别.对试验数据进行分析，最终确定了热水和常温养护条件下的τu的计算模型：

式中：界面咬合影响系数c为0.04，这是由于两种不同养护方式下的UHPC 配合比、骨料级配、浇筑方式和振捣器械等均相同.

目前，关于方钢管UHPC 黏结性能的试验较少，故采用公式（14）和（15）对本文试件进行计算，τu的计算与试验结果对比如图12所示，其中τua和τue分别为黏结强度计算和试验结果.两种养护制度下黏结强度计算值与试验值的相关系数的平方R2分别为0.92 和0.89，R2在0～1，越接近1 拟合精度越高，一般认为大于0.8 时，拟合结果较为理想［12］.故表明建议的模型可较准确地计算方钢管UHPC的黏结强度.

图12 计算值与试验结果的比较Fig.12 The comparison of calculated values with test results

5 结论

1）推出后的方钢管UHPC 试件总体较完整，钢管无鼓曲现象，不同宽厚比时钢管的约束作用不同，宽厚比较大时磨痕集中于界面角部，较小时则向截面中部移动，表明钢管的约束作用越强，界面摩擦力分布越趋于均匀.

2）试件加载端与滑移端的荷载（P）-滑移（S）曲线形状基本一致，且曲线分为有明显峰值点的弱化型和无明显峰值点的强化型两类.两类曲线均取加载端与自由端滑移量差值（ΔS）-加载端滑移（Sl）曲线斜率为零时对应的荷载为黏结破坏荷载Pu，此时内部UHPC产生整体滑移，试件达到黏结极限状态.

3）黏结强度τu随宽厚比和高宽比增加而减小，宽厚比较大时，τu随UHPC 强度的增大而提高，较小时其干缩现象明显，τu呈现先增后减的趋势；各试件黏结强度对应的黏结滑移量平均值约为1.77 mm，表明钢管UHPC 的界面黏结滑移较小，两者能够较好地协同工作承担荷载.

4）随着荷载增加，钢管纵向应变沿高度方向的差值增大，表明钢管UHPC 的协同工作性能逐渐减弱；加载端的钢管纵向应变小于自由端，对试验数据进行分析，发现钢管纵向应变沿高度方向大致呈指数分布.

5）忽略化学胶着力的影响，通过确定界面摩擦应力τf和机械咬合应力τw的数学表达式，建立了热水养护和常温养护条件下的τu计算模型，理论计算与试验结果符合较好.