考虑膨胀剂PEC 柱的黏结滑移性能

曹芙波 ， 谢 庆 ， 李 涛 ， 汪方莹 ， 王晨霞 ，*

（1.内蒙古科技大学土木工程学院，内蒙古包头 014010；2.内蒙古自治区高校智能建造与运维工程研究中心，内蒙古包头014010；3.中恒丰建筑集团有限公司，北京 102627；4.诺丁汉大学土木工程系，英国诺丁汉 NG72RD）

部分包裹混凝土（PEC）具有承载能力高、抗震性能好等优点［1］，因而得到了广泛的应用.型钢与混凝土之间足够的黏结力或设置的剪力连接件是保证两者共同工作的前提，这种作用力使钢-再生混凝土成为一种真正的组合结构［2］.

国内外许多学者已经对薄壁H 形钢焊接柱进行了广泛的试验研究，但大多数是研究焊接柱在不同加载条件下的行为［3-5］，结果表明PEC 的性能受到了薄钢腹板连接局部不稳定性的显著影响.Ning 等［6］研究了循环荷载下焊接H 形钢柱的抗震性能；Cao 等［7］进行了高强钢焊接H 形钢构件轴压下的局部屈曲行为研究；赵根田等［8-9］研究发现PEC 柱良好的耗能能力及抗震性能适用于抗震设防区的建筑结构中.还有学者针对型钢的黏结滑移性能进行了研究：郑华海等［10］对黏结阶段黏结应力的组成进行了分析；伍凯等［11］和柳战强等［12］发现了黏结长度对黏结性能的增强效应；秦艳［13］采用非线性弹簧单元，较好地模拟了型钢与混凝土之间的黏结性能.

本文设计了6 组考虑混凝土强度、黏结长度和膨胀剂掺量的试件，探究了无剪切连接件H 形钢与混凝土界面黏结力的组成，以确定其黏结滑移本构模型.

1 试验概况

1.1 试验材料及试件设计

采用 P·O 42.5 水泥（C）配制 3 种强度的混凝土，配合比及性能见表1.表1 中FA 为粉煤灰，MP 为矿粉，EA 为膨胀剂，fc和 fcu分别为 28 d 立方体抗压强度和28 d轴心抗压强度，E 为弹性模量.粗骨料采用机制碎石（G）；细骨料选用天然河砂（S），细度模数Mx=2.5，表观密度为2.65 g/cm3，含泥量（质量分数）为2.8%，中砂.外加剂选用聚羧酸高效引气减水剂（SP）；拌和水（W）采用城市自来水.H 形钢用Q235B级钢材焊接而成，钢筋采用直径8 mm 的HRB335 级钢材，材料性能见表2.表2 中σb和σs分别为钢材的抗拉强度和屈服强度，εs为屈服应变，μ 为泊松比，δ 为伸长率.考虑到负黏结力［14］的影响，测量位置从距离加载端50 mm 开始，距离自由端50 mm 结束，间距50 mm粘贴应变片.

表1 混凝土的配合比和性能Table 1 Mix proportions and properties of concretes

表2 钢材的性能Table 2 Properties of steel materials

GB 50018—2002《冷弯薄壁型钢结构技术规程》对于PEC 构件黏结性能的标准试件没有定义，且Chicoine 等［15］发现尺寸效应不会影响试件整体的破坏模式，即设计试件尺寸如图1所示，试件参数见表3.

表3 试件参数Table 3 Parameters of specimens

图1 PEC 推出试件Fig.1 PEC push-out specimen

1.2 试验加载

本文选择短柱推出试验，加载装置如图2所示.黏结力沿钢板分布是不均匀的，且无剪切件与系杆的存在使得黏结破坏的间隔较短，故加载制度选用位移加载控制，加载速率控制为0.2 mm/min.加载前首先预加荷载2 kN，避免因试件初始缺陷而造成的荷载损失.

图2 加载示意图及装置Fig.2 Loading diagram and device

2 结果及分析

2.1 荷载-滑移曲线

在黏结破坏过程的3 个阶段中，黏结力（P）的分布存在差异，在微滑移阶段极限状态有：

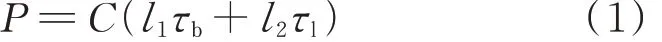
式中：C 为H 形钢与混凝土接触的截面周长，mm；l1为化学胶结力存在的区域长度，mm；τb为化学胶结力，MPa；l2为摩擦应力存在的区域长度，mm；τl为摩擦应力，MPa.

则在全滑移阶段中有：

式中：l为黏结长度，mm，且有l=l1+l2.

图3 为试件的荷载-滑移曲线.由图3 可见：随着混凝土强度的提高，混凝土的水灰比下降，更多的胶凝材料参与到界面反应中，使H 形钢与混凝土之间的黏结性能得到提高；黏结长度的提高使H 形钢与混凝土的接触面积增加，黏结效应得到增强，而黏结力分布是不均匀的，黏结长度的增加加剧了变形的不同步，这是不同黏结长度试件表现出差异性的原因；膨胀剂掺量的提高使两翼缘之间混凝土受到的挤压力增加，增强了黏结力；全滑移阶段中荷载缓慢增加，原因在于混凝土的泊松效应使H 形钢与混凝土之间的压力增加，增强了两者间的黏结性能.

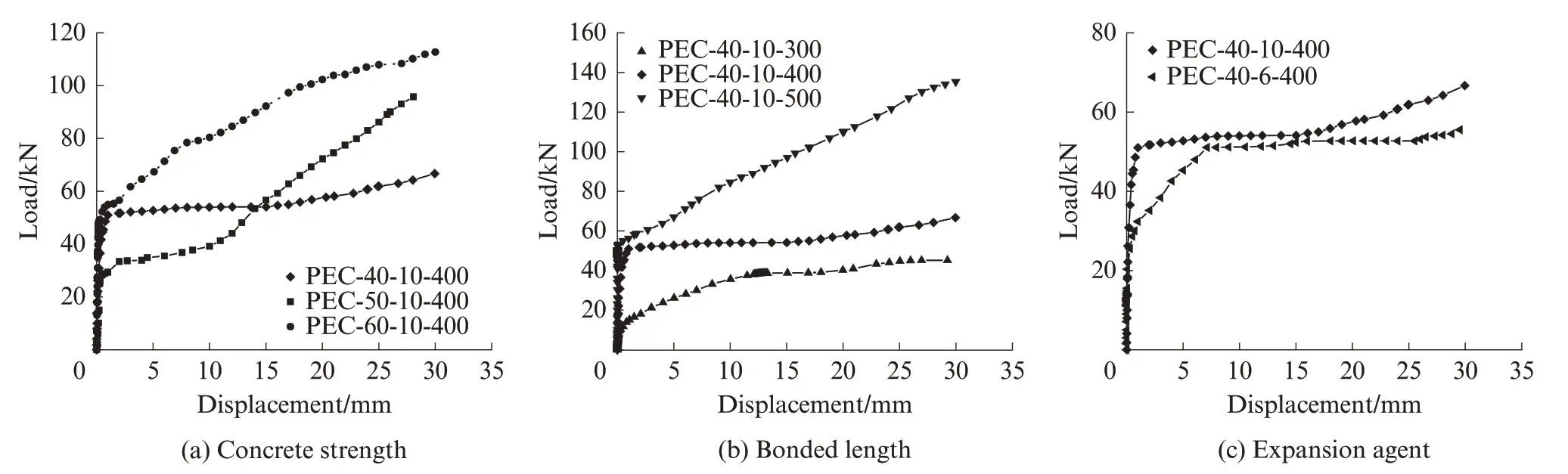
图3 试件的荷载-滑移曲线Fig.3 Curves of load-displacement of specimens

定义H 形钢与混凝土产生微滑移时的荷载为Ps，即初始黏结荷载；P0.8为滑移从微滑移转变为全滑移时对应的荷载值；Pu为破坏时的荷载值，即极限黏结荷载.通过式（3）将荷载值P 转化成H 形钢与混凝土间的平均黏结应力τ，即：

式中：H、B 分别为 H 形钢的高度和宽度，mm；t 为腹板或者翼缘厚度，mm.

Ps、P0.8、Pu对应的黏结应力 τs、τ0.8、τu见表 4，其中 S为破坏时的滑移值.

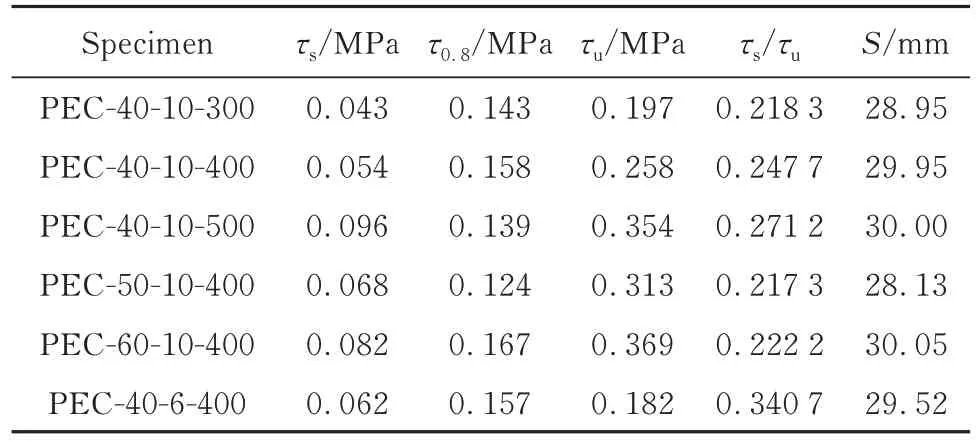
表4 特征黏结应力Table 4 Characteristic of bond stress

2.2 理论计算

在外荷载P 作用下，H 形钢和混凝土之间产生的黏结应力τ（x）在H 形钢黏结长度x 上的积分与外荷至自由端的部分形钢受力平衡，即有：

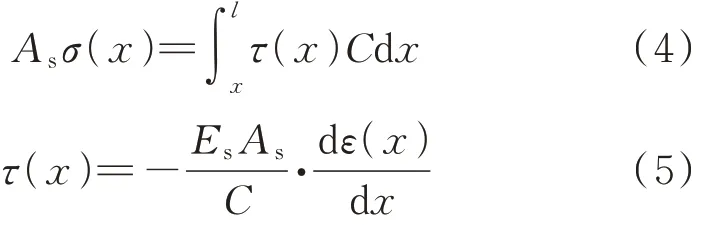
式中：σ 为 H 形钢上的应力，MPa；Es为 H 形钢的弹性模量，MPa；As为 H 形钢的受压面积，mm2.

2.3 化学胶结力和摩擦应力的求解

黏结应力经过黏结长度的传递后，H 形钢与混凝土之间无滑移，变形协调，应变差为零，在变形截面协调处有：

变形截面协调处混凝土受到的压力：

在变形截面协调处有εs=εc=ε，则混凝土所受到的压力为：

式中：Pc、Ps分别为变形截面协调处混凝土和H 形钢所受到的压力，kN；Ec、Es分别为混凝土和H 形钢的弹性模量，MPa，详细见表 1、2；Ac、As分别为混凝土的受压面积和 H 形钢的受压面积，mm2；εc、εs分别为变形截面协调处混凝土和H 形钢的应变；α 是H 形钢弹性模量与混凝土弹性模量的比值，H 形钢受压面积与混凝土受压面积的比值用β 表示.

式（2）表明在产生滑移阶段的黏结应力是摩擦应力，且x=l2，式（8）可变形：

混凝土能达到Ecεc的受压面积仅为全部受压面积的 25%［10］，结合式（1）、（2）、（9）与表 1～4，计算出l1、l2和 τl、τb，结果如表 5 所示 .由表 5 可见：

（1）H 形钢与混凝土之间的黏结应力主要由摩擦应力提供，整体上摩擦应力占到整个黏结应力的81.6%，摩擦应力是化学胶结力的数倍，在微滑移阶段考虑黏结应力区段长度的摩擦应力与化学胶结力的比值在0.41～0.47.在微滑移阶段，摩擦应力和化学胶结力保持稳定变化，说明不同参数下的黏结性能虽然差别较大，但是从黏结应力组成分析，黏结应力分布是相对稳定的.对比文献［10］中17 个试件发现，全包裹型钢混凝土结构也符合这个规律，除却试件SRRC-16 与试件SRRC-17，考虑黏结应力区段长度的摩擦应力与化学胶结力的比值稳定在0.48～0.52.

（2）C40 试件的摩擦应力是 0.158 MPa，随着混凝土强度的提高，摩擦应力呈现先降低再上升的趋势.相比于C40 试件，C50 试件的摩擦应力降低了21.5%，C60 试件的摩擦应力提高了5.6%，可能的原因是：混凝土的泊松效应使得H 形钢与混凝土之间的摩擦效应提高；混凝土强度的提高，更多的水泥基体参与到黏结界面中；混凝土浇筑过程中造成的水泥浆体不均匀分布降低了黏结界面处的黏结效应；几种因素的综合效应使摩擦应力变化表现出离散性和复杂性.C40、C50、C60 试件的化学胶结力分别为0.021、0.034、0.040 MPa，表明强度的增加使得 H 形钢与混凝土间的化学吸附程度增强，使更多的胶凝材料参与到H 形钢与混凝土界面处的反应中，增强了H 形钢与混凝土间的黏结性能.

（3）黏结长度为300 mm 试件的摩擦应力和化学胶结力分别是0.143、0.021 MPa，摩擦应力比黏结长度为400、500 mm 的试件分别提高了10.4%和-2.7%，化学胶结力分别提高了23.8% 和138.1%.随着黏结长度的增加，摩擦应力表现为先增加再减小，化学胶结力随着黏结长度的增加而增加，变化趋势不一致的原因是：黏结长度的增加会产生更多的劣性区域，且黏结应力沿黏结长度是不均匀分布的，胶凝材料的分布不均匀以及黏结长度的增加使黏结应力不能有效传递是导致变化存在差异的原因.

（4）膨胀剂掺量为10%试件的摩擦应力和化学胶结力分别为0.158、0.026 MPa，与膨胀剂掺量为6%试件的0.157、0.030 MPa相差0.001 MPa和-0.004 MPa.这表明随着膨胀剂掺量的变化，H 形钢与混凝土之间的黏结应力几乎没有变化.无剪切连接件H 形钢与混凝土的黏结应力主要由摩擦应力提供，由表5 可以看出不同参数试件的摩擦应力变化. 试件PEC-340-10-400 的摩擦应力为0.143 MPa，其他分别为 0.158、0.139、0.124、0.167、0.157 MPa，之间相差了-10.4%、2.7%、13.2%、-16.7%、-9.7%，表现出差异性的原因是参数的变化使得挤压力的大小产生了波动；在排除试验误差的情况下，可以通过提高混凝土强度、增加黏结长度来提高混凝土与H 形钢之间的黏结性能，这与文献［11］的研究结果相统一.

表5 黏结分布计算结果Table 5 Calculation results of bond distribution

3 黏结-滑移本构模型

3.1 平均黏结-滑移曲线

图4 为试件的平均黏结-滑移曲线.由图4 可见，无剪切件PEC 结构的黏结应力由摩擦应力和化学胶结力组成，在未滑移阶段，H 形钢与混凝土之间的黏结力由化学胶结力提供，在微滑移阶段，加载端监测到了滑移量，在距离加载端的一定区段内产生了滑移，H 形钢与混凝土产生了应变差，微滑移区段内H形钢与混凝土的界面黏结应力由摩擦应力提供.从表 4 分析可知，τs达到 τu的 20% 以上，稳定在 20%～35%内变化，在一定程度上说明研究参数的变化不会影响极限黏结强度与初始黏结强度的比值.

图4 试件的平均黏结-滑移曲线Fig.4 Average bond-slip curves of specimens

3.2 本构模型的建立

根据试验曲线变化趋势可知，PEC 黏结-滑移曲线3 个阶段（未滑移阶段、微滑移阶段和大滑移阶段）的变化形式符合直线段函数；所有试件表现出的破坏模式为推出破坏，建立折线段式PEC 黏结滑移本构模型，即为：

3.3 拟合曲线和试验曲线对比

图5 为试件的试验曲线与拟合曲线的对比.由图5 可见，折线式推出破坏本构模型很好地反映了H 形钢与混凝土之间的黏结性能，不同膨胀剂掺量试件在大滑移阶段出现的偏差在于推出破坏过程中化学胶结力退出工作，在小荷载作用下，H 形钢与混凝土脱离，表明仅通过H 形钢与混凝土之间的化学胶结力不足以保证H 形钢与混凝土之间黏结力的传递.

图5 试件试验曲线与拟合曲线的对比Fig.5 Comparison of test curves and fitting curves of specimens

试件PEC-50-10-400 黏结-滑移曲线的不一致在于加载过程中H 形钢与混凝土间接触压力的变化，使得其黏结-滑移曲线表现出差异性；混凝土沿腹板方向变形产生的泊松效应也使H 形钢与混凝土之间的黏结性能得到提高；混凝土强度的提高会使得泊松效应更加明显.

4 数值模拟

Abaqus 软件中可以通过定义非线性弹簧Spring2 来模拟H 形钢与混凝土的之间的黏结性能，确定应力与位移之间的关系.

4.1 前处理

（1）单元选择及材料属性：H 形钢和混凝土单元类型选取实体单元C3D8R，钢筋单元选取桁架单元T3D2，在划分网格阶段将钢筋单元设置成桁架Truss 单元；焊接H 形钢板与混凝土材料属性见表1和表2.对混凝土的压缩行为以及拉伸行为［18］进行定义，确定混凝土的拉伸和压缩下的损伤因子以及非弹性应变和开裂应变，试件尺寸参数见表3.

（2）分析步及作用：初始增量步设置为0.02，最小增量步默认为1×10-5，最大增量步为1 000 是满足计算要求的；在相互作用模块（Interaction），定义钢筋和箍筋组成的钢筋笼与混凝土的嵌入关系，在H 形钢底面和混凝土顶面设置参考点，耦合H 形钢表面并作用位移荷载；混凝土顶面设置成固定端.

（3）网格划分：网格划分时将H 形钢底板与H 形钢分割开分别划分网格，考虑到后期定义非线性弹簧单元节点的建立，在本文中定义混凝土与H 形钢的网格划分一致.

（4）定义非线性弹簧：应用Python 软件查询H形钢单元与混凝土单元的各连接点坐标，依据黏结-滑移曲线确定非线性弹簧F-D 之间的关系，对于黏结方向上的弹簧刚度依据黏结滑移模型确定，与黏结界面相对应的2 个方向上的弹簧刚度定义为无限大.

4.2 后处理

试件PEC-40-10-400 的Mises 应力云图见图6.由图6 可见，试件PEC-40-10-400 中H 形钢所受正应力由加载端向自由端逐渐减小，混凝土的应力变化则与之相反，这是由于仅有黏结接触提供混凝土与H形钢之间的黏结，而混凝土相当于自由端受力，因此表现出应力由加载端向自由端逐渐增加的趋势.

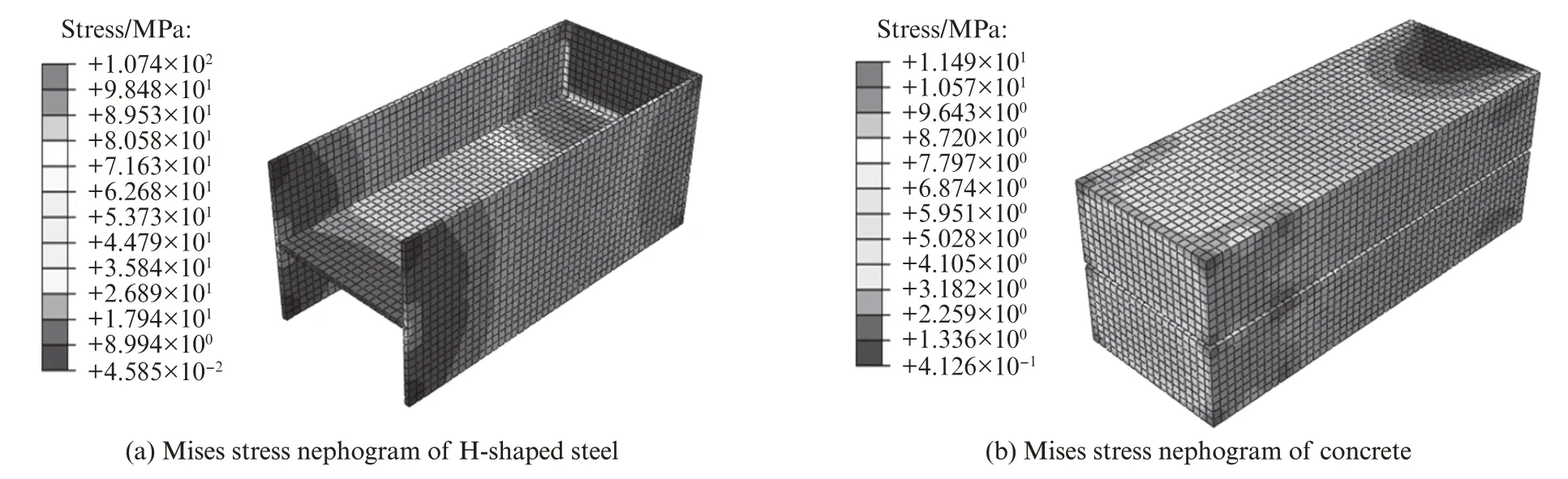
图6 试件PEC-40-10-400 的Mises 应力云图Fig.6 Mises stress nephogram of specimen PEC-40-10-400

图7 为试件黏结-滑移曲线模拟结果和试验结果的对比.由图7 可见，Abaqus 模拟结果与试验结果总体相符.

4.3 误差分析

通过图7 对比分析发现，初始黏结滑移强度模拟值偏大，原因是试验条件下的混凝土浇筑及振捣可能使界面处存在缝隙或空洞；滑移阶段后黏结强度的模拟值较试验值偏低，原因可能是GB 50010—2010《混凝土结构设计规范》定义的弹塑性行为与按照本试验配合比制备混凝土的弹塑性形为存在差异性.

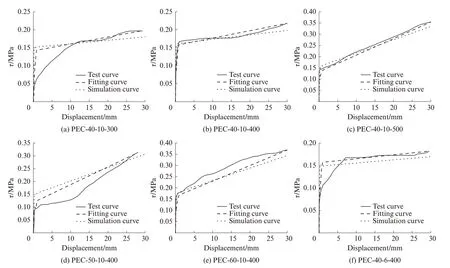
图7 试件黏结-滑移曲线模拟结果与试验结果的对比Fig.7 Comparison of simulation results and test data of bond-slip curves of specimens

5 结论

（1）黏结长度、混凝土强度和膨胀剂掺量与H 形钢与混凝土之间的黏结力呈正相关.排除试验误差以后，初始黏结强度与极限黏结强度的比值在20%～35%范围内保持稳定.

（2）H 形钢与混凝土之间的黏结应力主要由摩擦应力提供，摩擦应力是化学胶结力的294%，但在微滑移极限阶段，考虑黏结长度的摩擦应力是化学胶结力的42%～47%.

（3）折线式函数模型较好地反映了H 形钢与混凝土之间的黏结滑移本构；利用非线性弹簧建立的黏结滑移模型较好地反映了H 形钢与混凝土之间的黏结性能.