再生混凝土棱柱体与立方体抗压强度关系模型
高文昌 , 张 欢 ,*, 耿 悦 ,3, 杨 华
(1.哈尔滨工业大学土木工程学院,黑龙江哈尔滨 150090;2.哈尔滨工业大学结构工程灾变与控制教育部重点实验室,黑龙江哈尔滨 150090;3.华南理工大学广东省现代土木工程技术重点实验室,广东广州 510641)
随着中国工程建设的不断发展,建筑垃圾产量 不断上升,其中废弃混凝土约占30%~40%[1],其处置问题亟待解决.将废弃混凝土破碎筛分,形成再生骨料,进而制成再生混凝土,是提高建筑垃圾利用率、从根本上解决其处置问题的主要手段[2-3].现有研究[4-7]及工程实例[8]已证明再生混凝土在结构工程中的适用性.
根据GB 50010—2010《混凝土结构设计规范》,棱柱体抗压强度(fcp)是混凝土结构设计的核心参数,由立方体抗压强度(fcc)计算得到.因此,混凝土棱柱体与立方体抗压强度关系的准确性是结构安全设计的关键.现有研究[9-11]表明,再生骨料的掺入会显著改变混凝土棱柱体抗压强度与立方体抗压强度关系:再生骨料取代率(r)为 100% 时,fcp/fcc可发生-21%~37% 的变化[12-15].然而,已有再生混凝土棱柱体与立方体抗压强度关系模型[11-23]预测精度较低,模型间差异可达45%.
因 此 ,基 于 搜 集 的 13 篇 参 考 文 献[9,12,15,18,21-22,24-30]中共计139 组普通强度再生混凝土fcp与fcc试验数据,分析了以往模型离散性较大的原因,确定了再生骨料取代率(r)与吸水率(wa)这 2 个关键参数,并发现了二者的耦合效应.考虑上述影响因素,提出了再生混凝土棱柱体与立方体抗压强度关系预测模型;为方便使用,基于再生骨料分类,进一步提出了简化模型;最后系统地研究了模型不确定性的数据特征,为再生混凝土结构的可靠度分析提供了建议.
1 现有模型分析
目前,国内外学者已基于试验结果对再生混凝土 fcp与 fcc的关系模型开展了研究[11-23].马静等[12]、肖建庄[13]、姚大立等[16]、柴园园等[17]、吴淑海等[18]、向星赟等[19]通过试验结果拟合建立了再生混凝土fcp/fcc关系模型.上述模型认为fcp/fcc是常数,不随r 等参数变化,其 fcp/fcc预测结果范围为 0.67~0.85.而孟茁超等[11]、Zhou 等[14]、胡波等[20]、李旭平[21]、Zhang 等[22]考虑 r 的影响建立了fcp/fcc关系模型.此外,肖建庄等[23]在考虑r影响的同时,还引入了混凝土密度的影响.
现有再生混凝土棱柱体与立方体抗压强度关系模型预测结果对比见图1.由图1 可见,各模型预测结果之间差异较大,甚至趋势相反,最大相差可达45%.例如,在 Zhang 等[22]的模型中,fcp/fcc随 r 增大而降低;而在 Zhou 等[14]的模型中,fcp/fcc随 r 增大而增大 .上述显著差异主要由再生骨料物理性质差异[31]所致.上述模型建立过程中所用再生骨料的吸水率(wa)范围为2.7%~9.3%.然而,现有模型均是基于单一再生骨料来源提出的,不能反映再生骨料物理性质的影响.为此,有必要基于大量试验数据,分析再生骨料物理性质对再生混凝土fcp/fcc的影响,确定关键影响参数,提出考虑再生骨料物理性质影响的再生混凝土棱柱体与立方体抗压强度关系预测模型.
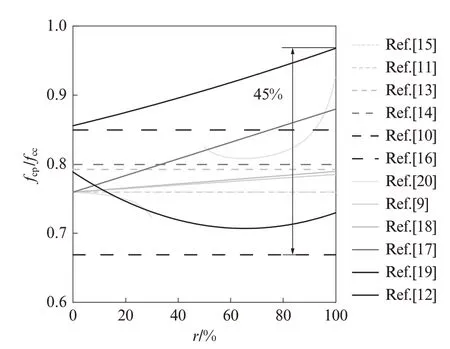
图1 现有再生混凝土棱柱体与立方体抗压强度关系模型预测结果对比Fig.1 Comparison of predicted results from different models for the relationship between prism and cube compressive strengths
2 关键参数确定
为确定影响再生混凝土棱柱体与立方体抗压强度关系的关键参数,搜集了13 篇参考文献[9,12,15,18,21-22,24-30]中共 139 组普通强度再生混凝土 fcp与fcc试验数据.为减小数据离散性,仅采用了无矿物掺和料且再生骨料未经强化处理的试验结果.搜集到的试验参数范围较广:水灰比(mw/mc)为0.35~0.57;fcc为 21~54 MPa;fcp为 15~44 MPa;r 为 0%~100%;wa为2.7%~9.3%.
通过系统分析发现,再生骨料取代率r 与吸水率wa是影响fcp/fcc的关键参数.图2 分析了再生骨料取代率r 与吸水率wa的影响.由图2 可见:当wa>8.0%时,与r=0%相比,r=100%时,fcp/fcc增大了27.1%;在r=100%的情况下,随着wa由3.0%增大到8.0%,fcp/fc增大了55.6%.

图2 再生骨料取代率和吸水率的影响Fig.2 Influence of recycled aggregate replacement ratio and water absorption ratio
由图2 还可以看出,r 与wa的影响存在显著的耦合效应,随着wa的增大,r 的影响趋势显著改变,甚至相反,即r 对fcp/fcc的影响由降低作用变为增大作用.例如:相对于r=0%的情况,对于wa<3.0%的再生骨料,r=100%时fcp/fcc降低了19.3%;而对于wa>8.0%的再生骨料,r=100%时fcp/fcc增大了27.1%.本文分析认为,该耦合效应主要是由r 与wa对混凝土断裂带的相反影响导致的.具体而言,对于相同配合比的混凝土,影响其抗压强度的关键因素为断裂带宽度与长度[32].混凝土断裂带越狭长,其应力释放区越大、有效承压部分越小,强度也就越低.随着混凝土形状由立方体变为棱柱体,其断裂带宽度未发生改变,而断裂带长度变大,从而导致混凝土棱柱体抗压强度低于立方体抗压强度,即 fcp/fcc<1[33].再生骨料的掺入会影响混凝土的断裂带宽度,进一步改变断裂带长度对强度影响的占比,从而影响fcp/fcc.再生骨料的影响主要表现在2 个方面:一方面,再生骨料表面附着大量的残余砂浆[34],r 的增大显著降低了混凝土中天然骨料的平均粒径[30],进而降低了断裂带宽度[33,35],从而增大了断裂带长度对强度影响的占比,最终起到降低fcp/fcc的作用.另一方面,由于再生骨料wa较大,一般需要引入附加水以保证混凝土的流动性[9,29,34].wa的增大会显著增大混凝土水灰比,降低水泥砂浆强度,增大断裂带宽度,从而降低断裂带长度对强度影响的占比,最终起到增大fcp/fcc的作用.因此,当wa较低时,主要表现为残余砂浆的影响,即随着r的增大,fcp/fcc降低;而当wa较高时,主要表现为附加水的影响,即随着r的增大,fcp/fcc增大.
数据分析结果显示,在参数范围内,fcp/fcc与混凝土fcc无显著关系.图3(a)、(b)分别给出了r=0%与r=100% 情况下混凝土立方体抗压强度的影响[9,12,15,18,21-22,24-30].由图 3 可以看出,普通、再生混凝土 fcp/fcc与fcc的关系趋势线均接近水平.该结果与现行规范GB 50010-2010 一致,即普通混凝土的fcp/fcc为常数.对比图3(a)、(b)可以看出,再生混凝土fcp/fcc的离散性大于普通混凝土.再生混凝土数据的变异系数(COV)为10.2%,大于普通混凝土的变异系数(7.0%).该差异主要是由再生骨料物理性质的离散性引起的.
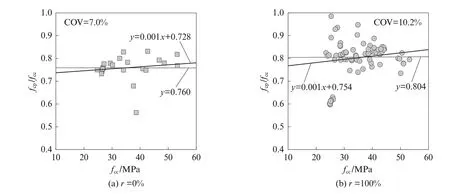
图3 混凝土立方体抗压强度的影响Fig.3 Influence of cube compressive strength
3 模型的建立与验证
为减小普通混凝土数据离散性造成的影响,通过建立再生混凝土fcp/fcc与普通混凝土fcp/fcc的关系,提出再生混凝土棱柱体与立方体抗压强度关系模型:

式中:αc1RAC、αc1NAC分别代表再生混凝土、普通混凝土的fcp/fcc;kRAC为再生混凝土修正系数.
考虑以下3 点来确定kRAC:当r=0%时,kRAC=1,此为边界条件;相同wa下,fcp/fcc与r呈线性关系(见图1);r 与 wa存 在 耦 合 效 应 .由 此 确 定 kRAC的 计 算 式如下:
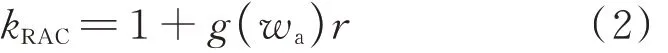
式中:g(wa)为再生骨料吸水率wa的函数.
为 确 定 g(wa)的 形 式 ,以 r=100% 的 试 验 结果[9,12,15,18,21-22,24-30]为 例 ,给 出 了 再 生 骨 料 吸 水 率 wa对kRAC的 影 响 ,见 图 4.由 图 4 可 见 ,wa与 kRAC为 对 数 关系,且拟合效果较好.

图4 再生骨料吸水率对kRAC的影响Fig.4 Influence of water absorption ratio of recycled aggregate on the factor kRAC
基于试验数据,采用对数形式对g(wa)进行回归分析:
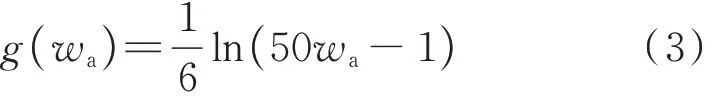
将式(2)、(3)代入式(1),得到再生混凝土棱柱体与立方体抗压强度关系模型:
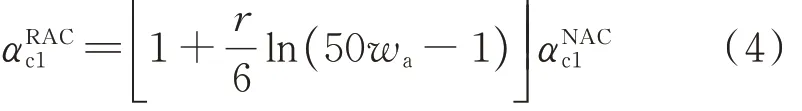
采 用 搜 集 的 13 篇 参 考 文 献[9,12,15,18,21-22,24-30]中 共139 组普通强度再生混凝土棱柱体抗压强度与立方体抗压强度试验数据,对所提模型(式(4))进行验证,结果见图 5.图 5 中,(fcp/fcc)exp为试验结果,(fcp/fcc)pre为模型预测结果.由图5 可见,所提模型可较好地预测再生混凝土棱柱体与立方体抗压强度关系fcp/fcc,99%的预测误差在±15%以内,预测结果与试验结果之比的平均值AVE=1.011,变异系数COV=5.4%.
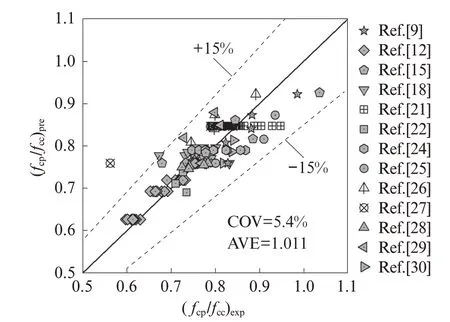
图5 所提模型预测结果与试验结果对比Fig.5 Comparison between the predicted results using the proposed model and experimental results
4 模型简化与验证
为方便设计人员使用,将基于再生骨料分类对所提模型(式(4))进行简化 .现行规范GB/T 25177—2010《混凝土用再生粗骨料》中,基于再生骨料性质将再生骨料分为Ⅰ、Ⅱ、Ⅲ类.而考虑到所搜集文献中提供的参数无法严格确定再生骨料分类,且数据分析结果显示wa为关键参数,简化模型采用GB/T 25177—2010 标准中基于吸水率的再生骨料分类,即:Ⅰ类,0%≤wa≤3%;Ⅱ类,3%<wa≤5%;Ⅲ类,5%<wa≤8%;wa>8%的再生骨料不宜应用.
对于Ⅱ类与Ⅲ类再生骨料,简化模型采用平均吸水率(Ⅱ类wa=4%,Ⅲ类wa=6.5%)作为代表值;考虑未经强化处理的再生骨料一般吸水率较高,采用2.5%作为Ⅰ类再生骨料吸水率代表值.将各类再生骨料的吸水率代表值代入式(4),得到仅有单一变量r的简化模型:

式中:kwa为基于吸水率的再生骨料分类系数,其取值如表1 所示.

表1 再生骨料分类系数kwa的取值Table 1 Values for recycled aggregate classification coefficient kwa
采用搜集的试验数 据[9,12,15,18,21-22,24-30]对简化模型进行验证,结果如图6所示.由图6可见,尽管对所提模型进行了简化,但是其仍具有较好的预测精度,预测结果与试验结果之比的平均值AVE=1.008,变异系数COV=5.8%,相对原始模型精度而言,降低不显著.
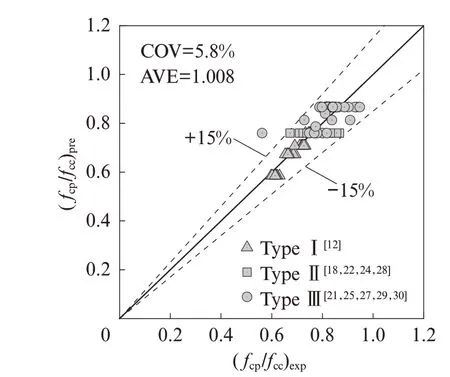
图6 简化模型预测结果与试验结果对比Fig.6 Comparison between the predicted results using the simplified model and experimental results
5 模型不确定性的统计分析及其与关键参数的相关性分析
5.1 统计分析
再生骨料来源多样、物理性质离散性高,导致再生混凝土力学性能具有较高的离散性[31].再生混凝土结构设计时应进行可靠度分析.模型不确定性的分布类型与分布参数的确定是可靠度分析的基础[36].基于搜集的试验数据[9,12,15,18,21-22,24-30],对所提模型开展不确定性的统计分析,以确定其分布类型.
为表征所提模型的不确定性,引入模型预测结果的偏差,作为随机变量θ.
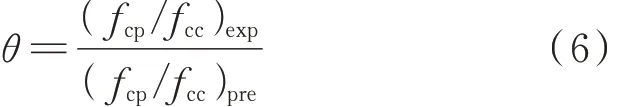
采用拟合优度检验与极大似然估计法,对随机变量θ 进行统计分析,结果见图7.由图7 可见,随机变量θ 的经验累积分布函数(ECDF)与拟合累积分布函数(CDF)吻合良好,结果可通过显著性水平为0.05 的A-D 和K-S 检验.这表明所提模型预测结果的不确定性服从正态分布,其平均值μ=1.011,标准差σ=0.054.
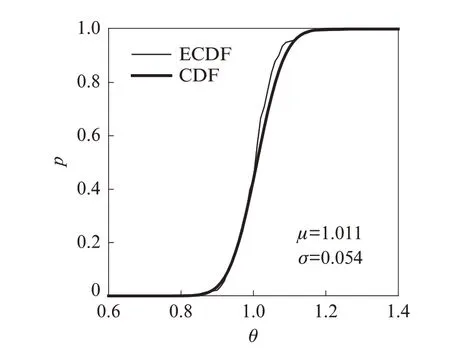
图7 随机变量θ 的统计分析结果Fig.7 Statistical analysis results of random variable θ
5.2 相关性分析
为提高可靠度分析结果的精确性,对随机变量θ与关键参数的相关性进行了分析[37].基于搜集的试验数据[9,12,15,18,21-22,24-30],采用 Pearson 相关系数(R),分析了随机变量 θ 与 r、fcc、wa、fcc之间的相关性,如图 8 所示.由图8可见,θ 与各参数无明显关系,R值在-0.013~0.022之间.Weber 等[38]指出,当|R|<0.35 时可认为各参数间的相关性较弱.该分析结果证明,所提模型已充分考虑了r与wa的影响,且证实了fcc对fcp/fcc无影响的结论.因此,在可靠度分析中可忽略所提模型与上述参数之间的相关性.
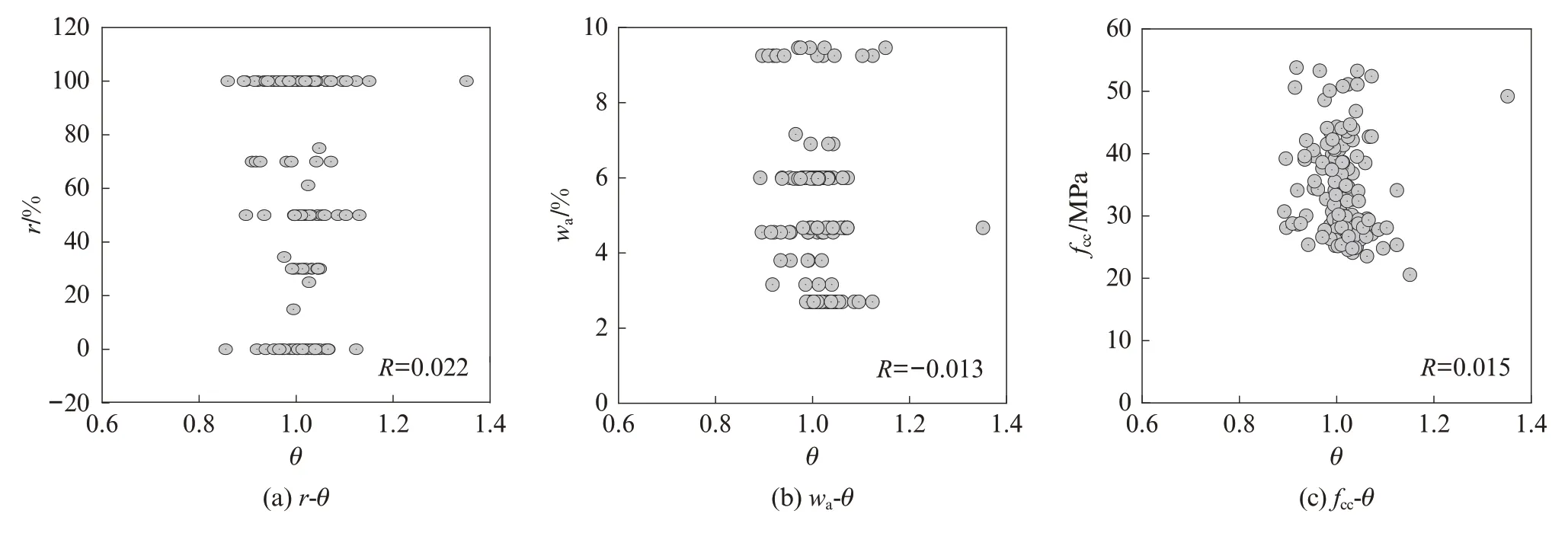
图8 θ 与关键参数的相关性Fig.8 Correlation between θ and the key parameters
6 结论
(1)基于对文献数据的系统分析,发现再生骨料取代率r、吸水率wa是影响再生混凝土棱柱体与立方体抗压强度之比fcp/fcc的关键参数,且二者之间存在显著的耦合效应,即不同wa下,r 的影响趋势不同,甚至相反.当0%≤wa≤3.0%时,r=100%相对于r=0%,fcp/fcc降低19.3%;而当 wa>8.0%时,r=100%相对于r=0%,fcp/fcc增大27.1%.
(2)基于试验数据,提出了考虑r、wa与二者耦合效应的再生混凝土棱柱体与立方体抗压强度关系预测模型.模型精度较高,预测结果与试验结果比值的平均值为1.011,变异系数为5.4%.为方便设计人员使用,基于再生骨料分类,进一步提出了再生混凝土棱柱体与立方体抗压强度关系简化模型.该简化模型形式简单,且精度并未显著降低,简化模型预测结果与试验结果比值的平均值为1.008,变异系数为5.8%.
(3)所提模型预测结果的不确定性服从正态分布,其平均值为1.011,标准差为0.054;且所提模型预测结果的不确定性与r、wa、fcc等参数的相关性较弱,相关系数在-0.013~0.022 之间.在可靠度分析中,可忽略上述参数对所提模型不确定性的影响.
(4)在模型建立过程中,所用试验结果中再生混凝土使用的是未经强化处理的再生骨料.在未来工作中,建议针对不同再生骨料强化处理方式的影响开展试验与理论研究,以验证和修正所提模型.

