考虑粗糙度和相对密实度下砂土-混凝土桩接触面力学特性试验研究
陈琛,冷伍明,2,杨奇,2†,徐方,3,魏丽敏,2
(1.中南大学土木工程学院,湖南长沙,410075;2.中南大学重载铁路工程结构教育部重点实验室,湖南长沙,410075;3.湖南铁院土木工程检测有限公司,湖南长沙,410075)
土体-结构物接触面相互作用问题广泛存在于实际工程中,如边坡挡墙支护、土钉、土工格栅-土体、桩土接触等[1-4].土体-结构物的相互作用在很大程度上是通过接触面的荷载传递来实现的.一直以来,关于土体-结构物接触面力学特性的研究被认为是解决土体-结构物二者相互作用问题的基础.其中涉及的非线性、大变形和局部不连续等力学问题,也是岩土工程中的难点和热点问题.因此,开展对土体-结构物接触面力学特性的研究既有理论意义又有工程应用价值.
国内外学者利用直剪、环剪等试验手段和DEM等数值仿真计算,就粗糙度、材料硬度、相对密实度、颗粒集配、磨圆度、含水率和法向应力等因素对土-结构物接触面力学特性的影响开展了诸多研究[5-10].在诸多影响因素中,接触面粗糙度一直被认为是影响界面剪切强度的重要因素之一,并得到广泛的关注.界面粗糙度被定义为“随机型”和“结构型”两类.对于“随机型”粗糙度,Uesugi 等[11]开展了砂土-混凝土接触面的直剪、单剪试验,研究发现接触面相对粗糙度存在临界值,接触面摩擦系数并非随相对粗糙度一直呈线性递增关系,当粗糙度大于该临界值时,摩擦因素将趋于砂土自身摩擦系数.Frost 和Han[12]通过直剪仪和改良的界面剪切设备,开展了砂土-纤维聚合物界面剪切特性的研究,研究发现结构物表面粗糙度、法向应力、初始密实度和颗粒形态对剪切强度有较大影响,而剪切速率和试样厚度则影响较小.Dove 和Frost[13]开展了渥太华砂、玻璃珠-聚乙烯土工膜界面剪切试验,基于接触力学和摩擦理论探究了颗粒形态、材料硬度对剪切机制的影响,结果表明材料表面的粗糙度与材料硬度存在相互耦合,共同影响接触面力学特性,在高法向应力下的软质表面,不可忽视颗粒形态所产生的“犁滑作用”对剪切强度的贡献.Han 等[14]利用界面直剪实验开展了接触面粗糙度、颗粒几何形态和集配对砂土-不同锈蚀程度钢板接触面摩擦角的影响研究.对于“结构型”粗糙度,Hryciw 和Irsyam[15]开展了砂土-带肋钢板接触面的直剪试验,研究发现存在最优的肋间距,既可避免剪切中颗粒堵塞凹槽,又可以充分调动土体参与变形协调而形成“被动阻力”.Chen 等[16]基于规则型粗糙度的形态特征提出了改进的灌砂法来量定界面粗糙度,利用大型直剪仪开展了红黏土-混凝土接触面界面剪切试验,试验结果表明粗糙度对界面剪切强度有显著影响,接触面峰值强度随粗糙度增加而增大.
现场试验表明土体的相对密实度对土体-结构物的摩擦阻力产生较大的影响,对于灌注桩和连续墙等结构尤其如此[17-20].目前,有关相对密实度对土体-结构物接触面力学特性影响的研究如下:Fakhar⁃ian 等[21]通过直剪仪开展了不同密实度下砂土-粗糙钢板力学特性研究,研究发现初始密实度、法向应力和恒定的法向刚度对接触面摩阻力和破坏时剪切位移有较大影响,并就不同密实度下滑动摩擦、剪切破坏发生阶段与剪切应力-切向位移曲线对应关系进行了定量划分;O'rourke 等[22]利用大型直剪仪,研究了土体密实度对砂土-聚合物界面特性的影响;王军等[23]通过大型单调直剪、循环直剪试验研究不同密实度下的砂土-格栅界面剪切特性,发现密砂-格栅界面发生剪切软化现象,密实度增加会提高筋土界面抗剪强度,剪胀增强.综上所述,尽管有不少学者开展了界面粗糙度对土体-结构物接触面剪切特性影响的研究,但试验中所设计的结构物凹凸深度较小(0.001~10 mm),且与实际工程中结构物粗糙度缺乏关联,难以表征和模拟如灌注桩、地下连续墙等结构物表面粗糙度.此外,对于相对密实度的研究,现有文献缺乏系统和清晰的认知.“规则型”混凝土表面粗糙度与相对密实度对砂土-混凝土接触面力学特性的影响研究鲜有报道.
鉴于此,本文利用现场钻孔灌注桩的粗糙度分布概率,基于灌砂法基本原理,构建了表面光滑和规则型粗糙混凝土板来模拟实际桩侧表面粗糙度.开展了不同密实度下砂土-混凝土接触面的大型直剪试验,研究了粗糙度、相对密实度对砂土-混凝土接触面剪切应力-切向位移关系、峰值剪切强度、割线摩擦角、峰值界面摩擦系数等影响规律.试验成果对深入了解土体-混凝土接触面力学特性、构建土体-结构物接触面本构模型具有重要意义.
1 试验方案
1.1 试验设备
试验采用位于高速铁路建造技术国家研究中心实验室内的TYJ-800大型直剪仪.仪器主要由4个部分组成,分别是液压伺服单元、测控单元、加载单元、制作单元,如图1 所示.该设备采用全数字环闭控制系统,可实现自动化采集数据.上、下剪切盒尺寸长×宽×高为:500 mm×500 mm×150 mm.在进行界面直剪试验时,以结构物替换下剪切盒,安置在由钢板、螺杆和螺母组成的结构物升降板上,通过调节高度使结构物与上剪切盒贴合,如图2所示.

图1 大型界面直剪仪器主要单元Fig.1 Main element of large-scale shear apparatus
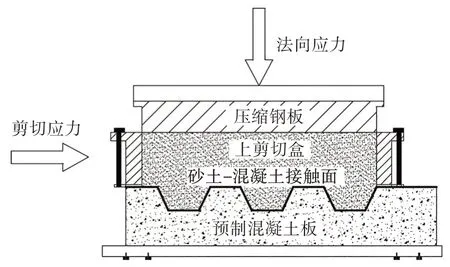
图2 砂土-混凝土接触面示意图Fig.2 Schematic view of cross section of sand-concrete interface
1.2 试验材料制备
1.2.1 砂土
试验用土为湖南湘江河砂,级配曲线如图3所示.依据颗粒分析试验和美国规范ASTM D2487-17e1[24]确定为粗砂,平均粒径D50=0.75,最大孔隙比emax=0.73,最小孔隙比emin=0.43,相对密度Gs=2.55,砂土试样含水率w为12%.详细基础物理参数如表1所示.
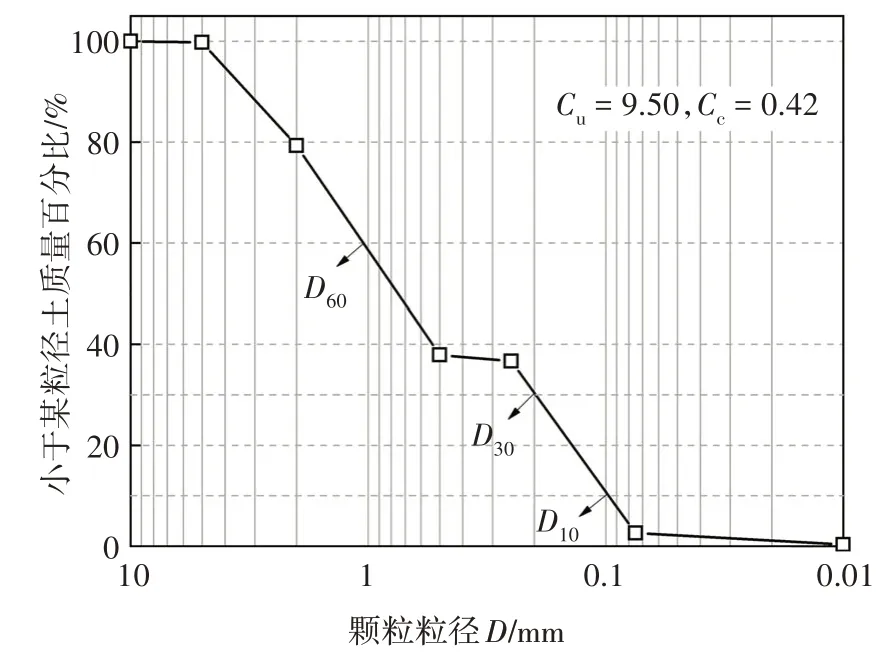
图3 湘江河砂级配曲线Fig.3 Particle size distribution of Xiangjiang River sand
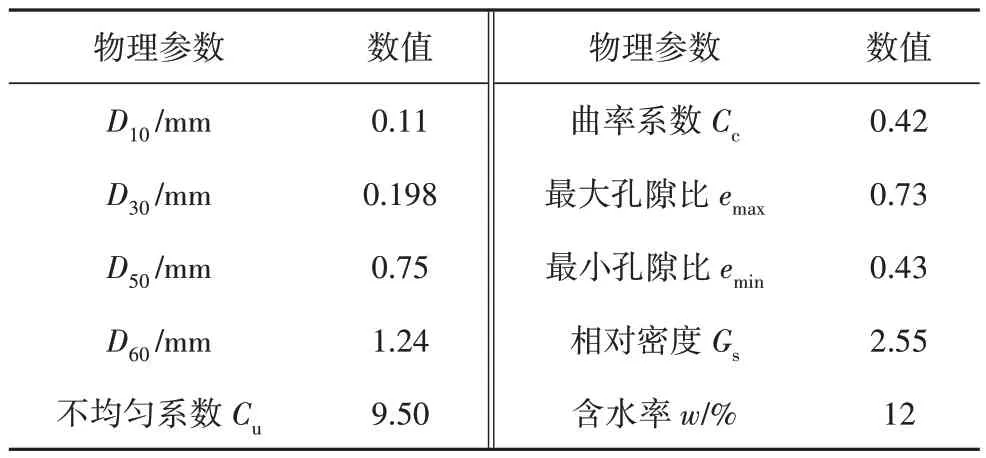
表1 湘江河砂基础物理力学参数Tab.1 Basic physical and mechanical properties of Xiangjiang River sand
为探究密实度对砂土-混凝土接触面力学特性的影响,设置相对密实度Dr为73%、47%和23%分别对应密实、中密和松砂3 种状态.为保证试验中砂土试样的相对密实度,推导出填筑砂样质量ms与相对密实度Dr、试样体积v的关系式,可表示为:
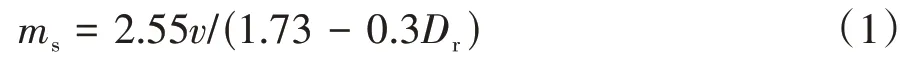
预设试样初始相对密实度为73%、47%和23%,对应孔隙率为0.51、0.59、0.66,根据混凝土板凹槽尺寸和上剪切盒体积计算得到试样填装质量.
1.2.2 混凝土板
根据文献[5]中的方法,基于现场钻孔灌注桩孔径检测结果,统计得到桩径与径向凸出尺寸的总体分布概率,利用灌砂法来建立桩侧粗糙度I与径向凸出尺寸的关系,计算后选取分布概率较大的粗糙度表征值10 mm、20 mm、30 mm 作为试验混凝土板的粗糙度值.为模拟混凝土预制桩表面粗糙度,制作了一块表面无凹槽的光滑混凝土板;为模拟灌注桩桩侧表面的粗糙度,在混凝土板表面设置了梯形凹槽结构,如图4 所示.利用混凝土板槽深h与桩侧粗糙度I的关系[5],得到相应混凝土梯形凹槽对应高度h分别为20 mm、40 mm、60 mm.采用C50 混凝土制作长×宽×高为570 mm×570 mm×100 mm 的混凝土板,如图5所示.
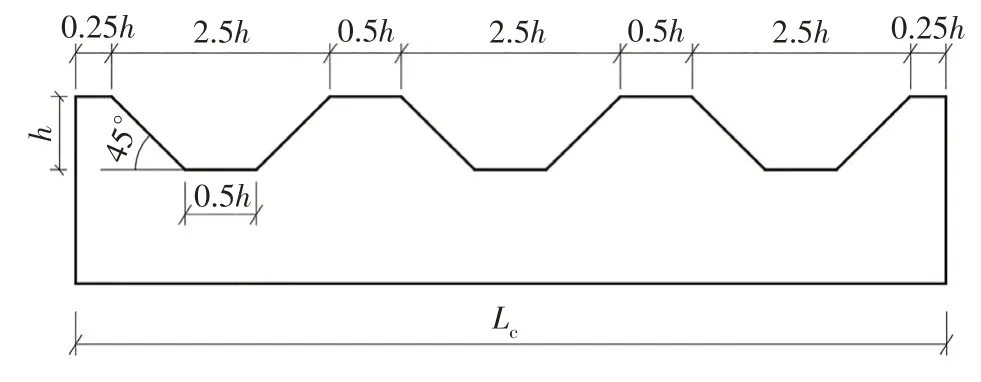
图4 混凝土板截面尺寸Fig.4 Section size of concrete block

图5 预制混凝土板试样Fig.5 Concrete blocks with different roughness
1.3 试验过程及加载方案
将混凝土板安放在大型直剪仪升降台上,然后安装上剪切盒,调节升降台高度使混凝土板上沿与上剪切盒下沿紧挨.根据公式(1)按照试样的预设相对密实度、混凝土板凹槽尺寸和上剪切盒体积计算得到试样填装质量,将试样砂土分三层填筑,依据填筑高度计算得到每次填筑砂土的质量,利用夯锤逐层压实至指定高度,以确保均匀和密实,最终达到设定相对密实度.一般灌注桩的设计长度小于60 m,为贴近实际工程情况,试验加载的法向应力确定为50 kPa、150 kPa、250 kPa 和350 kPa.剪切过程中,剪切速率设置为1.0 mm/min[25].当剪切位移u达到50 mm时,终止试验.具体试验方案见表2.

表2 砂土-混凝土接触面直剪试验方案Tab.2 Testing programs for sand-concrete interface
2 试验结果及分析
2.1 剪切应力-切向位移
2.1.1 砂土自剪结果
通过大型直剪试验获得不同相对密实度砂土自剪试验结果,选取密砂、松砂试样的剪切应力-切向位移关系曲线进行对比,如图6所示.

图6 不同密实度下砂土剪切应力-切向位移变化曲线Fig.6 Curves of shear stress-horizontal displacement of sand sample with different densities
由图6 可知,不同法向应力下密砂的剪切应力-切向位移关系曲线总体呈软化型.剪切应力随切向位移的增加而增大,达到峰值后逐渐衰减,并趋于稳定的残余剪切状态.法向应力越大,峰值强度越大,其对应的切向位移也越大.相反,松砂的剪切应力-切向位移关系曲线表现为硬化型.剪切应力随着切向位移增加在初期增长较快,而后增长速率减缓至0,剪切应力也随之保持稳定.由此可见,相对密实度对砂土剪切应力-切向位移关系曲线发展形式和剪切强度大小有较大影响.
2.1.2 砂土-混凝土接触面直剪试验结果
通过砂土-混凝土接触面直剪试验,获得密砂、松砂接触面直剪试验的剪切应力-切向位移关系曲线,如图7所示.


图7 不同相对密实度下(Dr≈73%,23%)砂土-混凝土接触面剪切应力-切向位移变化关系曲线Fig.7 Curves of shear stress-horizontal displacement of sand-concrete interface with different relative densities(Dr≈73%,23%)
由图7(a)可知,对于光滑接触面,密砂的剪切应力在初期随切向位移增大而近似线性增长,达到峰值后出现轻微衰减,而后保持稳定.剪切应力-切向位移曲线表现为轻微软化型.由图7(b)~(d)可知,随着粗糙度增加,密砂的剪切应力-切向位移曲线转变为明显的软化型.剪切应力达到峰值后,出现明显的峰后衰减,最终趋于稳定状态.此外,粗糙度的增加同时导致剪切应力峰后衰减幅度的降低,即接触面的软化特征随粗糙度增加而减弱.例如当粗糙度I=30 mm 时,法向应力50 kPa、150 kPa、250 kPa、350 kPa 对应峰值强度分别为76.44 kPa、157.24 kPa、214.92 kPa、264.52 kPa,至残余强度的衰减率分别为8.79%、11.77%、9.32%、3.51%.这与文献[26]所得结论相一致.这说明对密砂而言,接触面粗糙度对剪切应力-切向位移曲线的发展程度影响较大.
相同粗糙度下,密砂达到峰值强度所需切向位移随法向应力的增大而增加.相同法向应力下,密砂达到峰值强度所需切向位移随粗糙度增加而增大.这是由于粗糙度的增加,导致土体颗粒与结构面接触面积增大,参与剪切过程中变形协调的土体范围也增加,从而达到破坏状态所需要的切向位移亦随之增加.对于松砂,随着粗糙度增加,其剪切应力-切向位移曲线表现出硬化型特征.
综上所述,粗糙度对砂土-混凝土接触面的剪切应力-切向位移曲线的发展形式影响较小,而相对密实度则对该曲线发展形式起主导作用.
2.2 接触面强度指标参数分析
2.2.1 接触面峰值剪切强度
为分析粗糙度和相对密实度对砂土-混凝土接触面剪切强度的影响,对于不同相对密实度下砂土-混凝土接触面的切向位移-剪切应力关系曲线,分别取软化型曲线的峰值强度和硬化型曲线的剪切应力最大值作为接触面的峰值剪切强度,如表3 所示.根据表3 得到不同相对密实度下接触面峰值剪切强度-法向应力关系曲线,如图8所示.
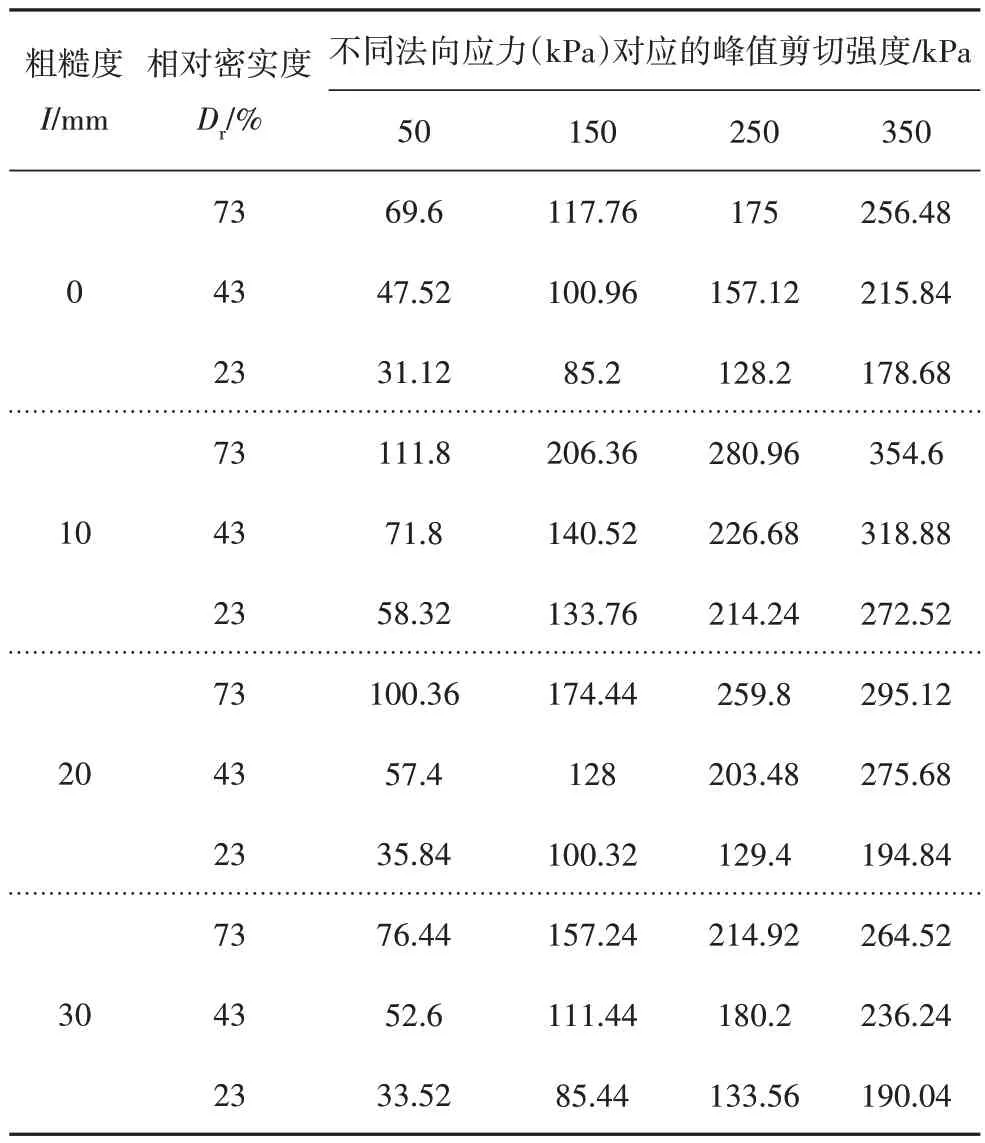
表3 砂土-混凝土接触面峰值剪切强度Tab.3 Peak shear strength of sand-concrete interface
由图8 可知,在相同粗糙度下,砂土-混凝土接触面峰值剪切强度随法向应力增加近似非线性增长.相对密实度越大,峰值剪切强度非线性增长越明显.Frost 和Han[12]在砂土-纤维聚合物界面直剪试验中也发现类似结论.周国庆等[27]和Hosseini 等[28]将这种现象归结于界面土体的剪胀变化.相对密实度较大的土体,剪切过程中颗粒间容易出现破碎,随着法向应力增加,剪胀性减小,颗粒间翻滚、嵌入与摩擦程度降低,导致峰值剪切强度的变化增量减小.此外,同一相对密实度下,接触面峰值剪切强度随法向应力增加所产生的变化增量逐渐降低.例如相对密实度Dr=73%下,法向应力由50 kPa增至350 kPa,粗糙度I=10 mm 的峰值剪切强度变化增量分别为84.57%、36.15%、26.21%.
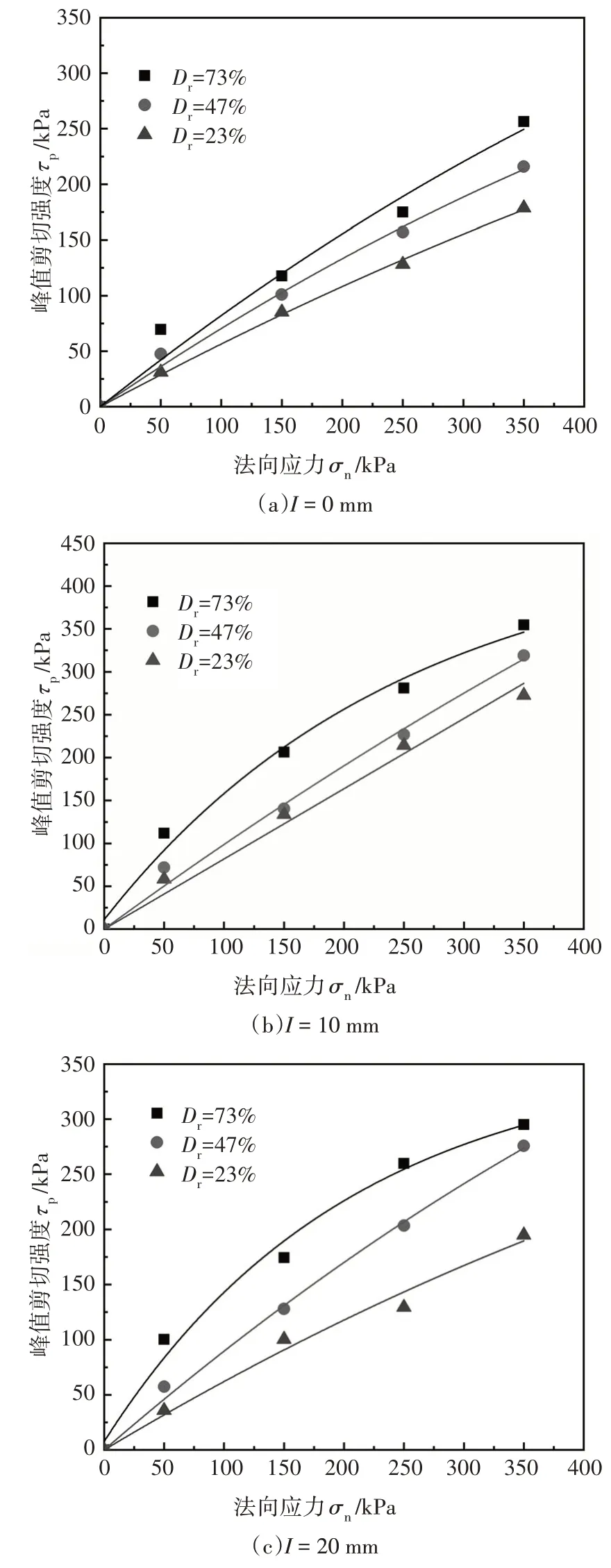

图8 不同相对密实度下接触面峰值剪切强度-法向应力的变化曲线Fig.8 Curves of interface peak shear stress-normal stress with different relative densities
相对密实度在一定程度上影响砂土-混凝土接触面的剪切强度关系,在理论计算和数值仿真中应根据实际受力情况及土体密实程度、结构物粗糙度等情况构建本构方程[28].
2.2.2 接触面割线摩擦角
由于不同相对密实度下砂土-混凝土接触面峰值剪切强度-法向应力的变化曲线存在一定的非线性,通常采用割线摩擦角φsec来表征接触面的强度指标[29].由图8 获得不同相对密实度下砂土-混凝土接触面割线摩擦角,通过数据拟合得到接触面割线摩擦角-法向应力的关系曲线,如图9 所示.拟合曲线相关系数R2>0.903 1,相关性较好,割线摩擦角与法向应力的拟合方程可以表示为:
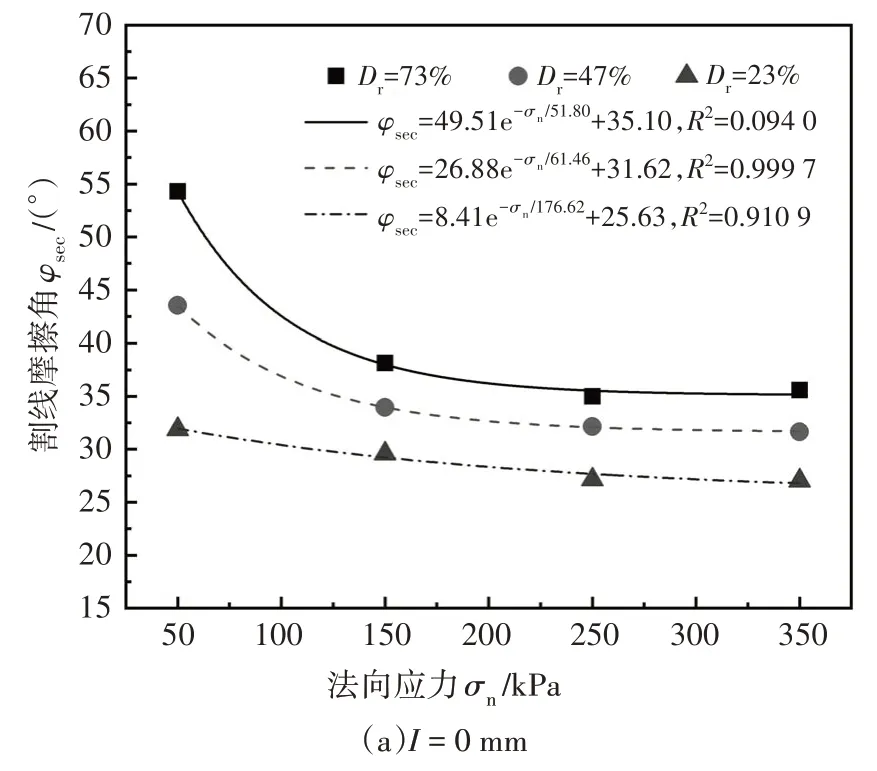
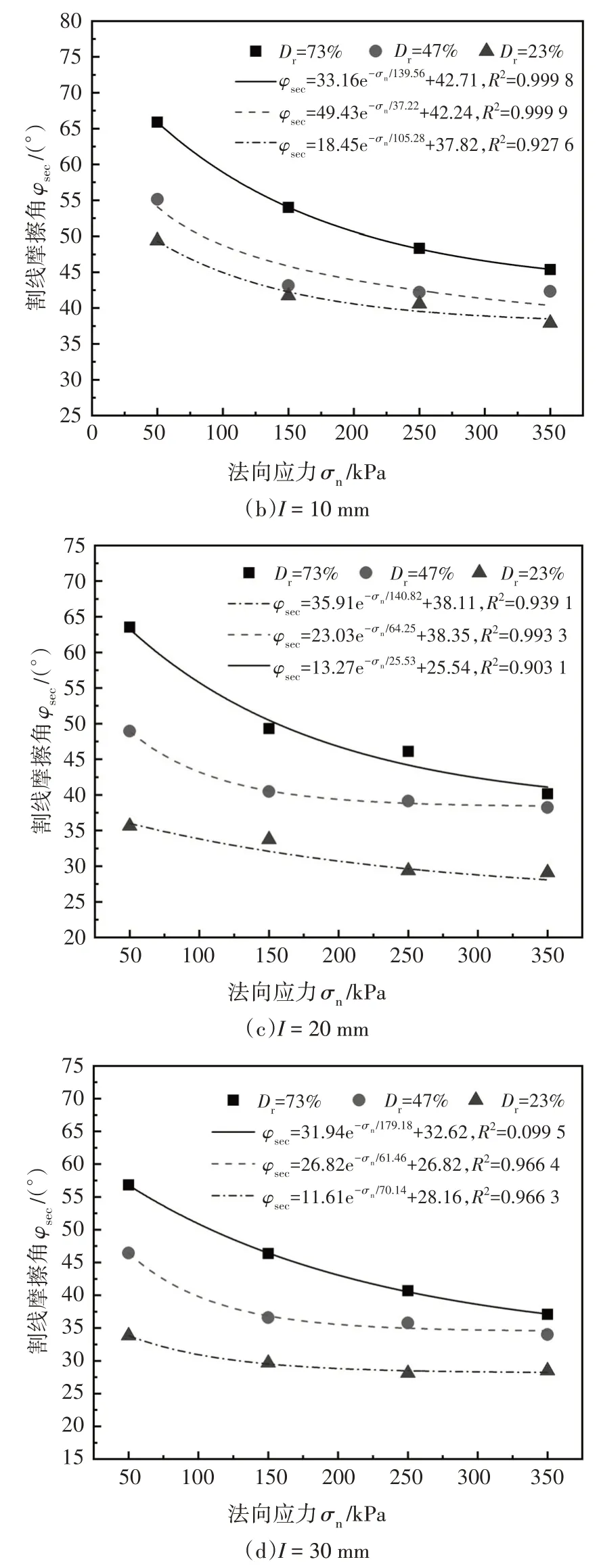
图9 不同相对密实度下割线摩擦角-法向应力的变化曲线Fig.9 Curves of secant friction angle-normal stress with different relative densities

式中:φsec为接触面割线摩擦角;σn为法向应力;A、B、C为拟合参数,可通过数据回归分析获得.
分析图9 可知,在相同粗糙度下,接触面割线摩擦角随法向应力增加近似呈指数衰减,割线摩擦角的衰减速率先增大后变小.例如,当I=0 mm 时,法向应力由50 kPa 增至350 kPa,Dr=73%试样的割线摩擦角对应的衰减率分别为22.05%、5.27%、1.52%.在相同法向应力下,相对密实度越大,接触面割线摩擦角越大,法向应力增加导致割线摩擦角随相对密实度变化的衰减速率越小.I=20 mm,法向应力在50 kPa 和350 kPa 时,Dr=73%、47%、23%对应割线摩擦角衰减速率分别为22.37%、17.28%、5.30% 和12.93%、2.32%、0.82%.说明相对密实度降低会减小接触面割线摩擦角对法向应力影响的敏感性.
2.2.3 接触面峰值界面摩擦系数
桩-土接触面力学特性除了可以用峰值剪切强度τp和接触面割线摩擦角φsec表征外,还可以由界面摩擦系数μp来反映.为了直观反映法向应力和粗糙度对接触面摩擦系数的影响,本文采用峰值界面摩擦系数μp[30]表征砂土-混凝土接触面抗剪强度特性.峰值界面摩擦系数μp可定义为峰值剪切强度τp与所施加法向应力σn的比值,表达式如下:

根据表3 和公式(3)计算得到不同相对密实度下砂土-混凝土接触面及砂土自剪峰值界面摩擦系数,如表4所示.基于表4结果,采用最小二乘法拟合获得砂土-混凝土接触面及砂土自剪峰值界面摩擦系数与法向应力的变化曲线,如图10 所示.拟合相关系数R2>0.89,相关性较好,峰值界面摩擦系数与法向应力的拟合方程可表示为:
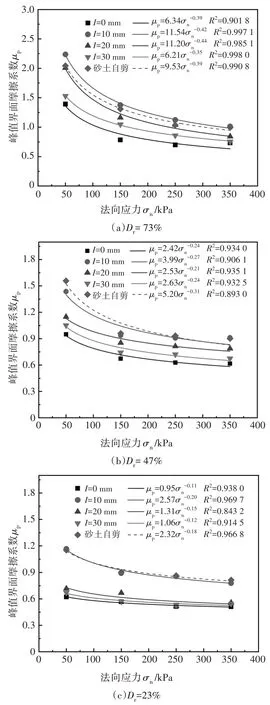
图10 接触面峰值界面摩擦系数-法向应力变化Fig.10 Curves of peak friction coefficient-normal stress of the interface
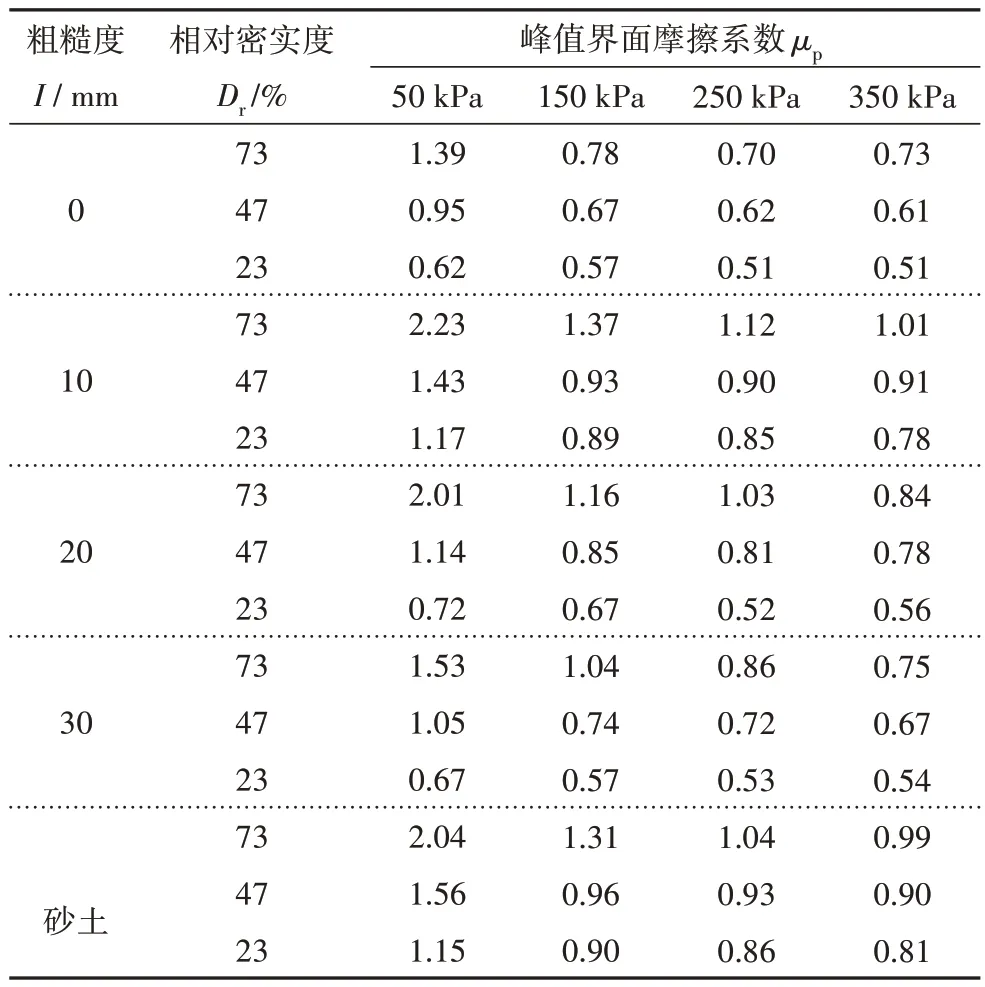
表4 砂土-混凝土接触面峰值界面摩擦系数Tab.4 Peak friction coefficient of sand-concrete interface

式中:μp为峰值界面摩擦系数;σn为法向应力;A、B为拟合系数,表征峰值界面摩擦系数μp随法向应力的增大而衰减的程度.
由表4、图10可知,不同相对密实度下峰值界面摩擦系数随法向应力增加近似呈幂函数衰减,法向应力越大,峰值界面摩擦系数衰减速率越小.例如粗糙度I=20 mm时,σn由50 kPa增加至150 kPa,Dr=73%的试样对应的μp由2.01减小为1.16,衰减率为42.29%;而σn由150 kPa增加至350 kPa时,μp衰减率为27.5%.
尽管峰值界面摩擦系数随法向应力增加而衰减,但并不说明接触面剪切强度的降低.由2.1 节分析可知,相同粗糙度下,法向应力越大,接触面抗剪强度越高.其规律可以解释为:随法向应力σn的增加,峰值剪切强度τp的增量变化较小,导致τp/σn的比值减小,即使得峰值界面摩擦系数μp在高法应力下作用逐渐趋于平稳.此时法向应力增量引起的峰值剪切强度τp增量变大,导致峰值界面摩擦系数不会持续减小.这一规律与张玲等[31]、王协群等[32]的研究中所得结论相一致.
此外,粗糙度对峰值界面摩擦系数影响较大.不同相对密实度下,峰值界面摩擦系数满足的关系,其中表示粗糙度为x的峰值界面摩擦系数.由此可知,存在临界粗糙度Icr=10 mm,当粗糙度I 为了分析粗糙度对接触面力学特性的影响,并判断剪切过程中接触面的剪切破坏位置,采用归一化割线摩擦角φsec/φs来表征砂土-混凝土接触面抗剪强度.其中,φsec为接触面割线摩擦角;φs为相同密实度下砂土割线摩擦角,具体参数见表5. 表5 砂土-混凝土接触面割线摩擦角Tab.5 Secant friction angle of sand-concrete interface 图11 为不同法向应力下砂土-混凝土接触面归一化割线摩擦角-粗糙度关系曲线.由图11 可知,不同密实度下,归一化割线摩擦角随着粗糙度增加(0 mm→10 mm)而增大,后随粗糙度增加(10 mm→30 mm)而减小.归一化割线摩擦角随粗糙度的变化规律同样证明了临界粗糙度Icr的存在.即当I 图11 接触面归一化割线摩擦角-粗糙度变化曲线Fig.11 Curves of normalized secant friction angle-roughness of the interface 砂土-混凝土接触面剪切破坏位置常通过接触面剪切强度与砂土自剪强度的大小来判断,剪切破坏面常发生在抗剪强度相对较小的位置.对于中密、松砂而言,归一化割线摩擦角φsec/φs始终小于1.0,即说明接触面抗剪强度要小于砂土自剪强度,此时剪切破坏面可能发生在接触面上.而对于密砂而言,归一化割线摩擦角φsec/φs更接近1.0;当达到临界粗糙度Icr时,φsec/φs超过1.0.这说明接触面抗剪强度要大于砂土自剪强度,此时剪切破坏面可能发生在土体中. 由表5 绘制得到不同法向应力下砂土-混凝土接触面割线摩擦角-相对密实度的变化曲线,如图12所示.由图12 可知,相同法向应力下,接触面割线摩擦角随相对密实度的增大而增加.例如法向应力σn=50 kPa 时,粗糙度I=10 mm 的试样相对密实度为23%、47%、73%,对应的接触面割线摩擦角为49.39°、55.14°、65.9°.通过数据拟合得到割线摩擦角与相对密实度的变化曲线,发现二者存在良好的线性关系,相关系数R2>0.803 5.其拟合方程为: 图12 接触面割线摩擦角-相对密实度变化曲线Fig.12 Curves of secant friction angle-relative density of the interface 式中:A、B均为拟合参数,分别表征接触面割线摩擦角φsec随相对密实度增大而增加的程度以及除相对密实度外的其他因素对割线摩擦角φsec的影响. 相同粗糙度下,接触面割线摩擦角φsec的增长速率随法向应力增加逐渐减小.例如在粗糙度I=10 mm下,法向应力50~350 kPa 对应的接触面割线摩擦角φsec的增长速率分为33.43%、29.38%、19.70%、19.06%.相同法向应力下,无论相对密实度如何变化,光滑接触面的割线摩擦角始终是下限值,而临界粗糙度Icr=10 mm的接触面割线摩擦角始终是上限值. 本文利用现场实测桩径曲线所获的桩侧粗糙度分布频率,构建了可模拟实际桩侧粗糙度的混凝土接触面.采用大型直剪仪开展了砂土-混凝土接触面直剪试验,探究了不同粗糙度和相对密实度对砂土-混凝土接触面力学特性的影响规律.主要研究结论如下: 1)密砂在光滑接触面下,剪切应力-切向位移曲线呈轻微软化,随着粗糙度增加,曲线软化趋势越明显.密砂达到峰值强度所需切向位移随法向应力、粗糙度增加而增大.松砂的剪切应力-切向位移曲线始终呈硬化趋势.密实度对剪切应力-切向位移曲线发展形式起主导作用,而粗糙度对曲线的发展程度影响较大. 2)界面峰值剪切强度随法向应力增加近似非线性增长,相对密实度越大,非线性增长越明显.接触面割线摩擦角随法向应力增加呈指数衰减,但随相对密实度增加呈线性增长.相同粗糙度下,相对密实度越大,接触面割线摩擦角越大. 3)不同相对密实度下接触面峰值界面摩擦系数则随法向应力增加呈幂函数衰减,衰减速率逐渐减小,这并不代表剪切强度的减小,而是剪切强度的增量变化较小所导致.光滑接触面的峰值界面摩擦系数始终是砂土-混凝土接触面的下限值,砂土自剪的峰值界面摩擦系数却不总是其上限值.对密砂而言,当粗糙度达到临界值时,容易产生“被动阻力”,使得砂土-混凝土接触面峰值界面摩擦系数超过砂土自剪的峰值界面摩擦系数;对中密砂、松砂而言,砂土自剪的峰值界面摩擦系数仍然是其上限值. 4)存在临界粗糙度Icr,当I2.3 粗糙度对接触面力学特性的影响
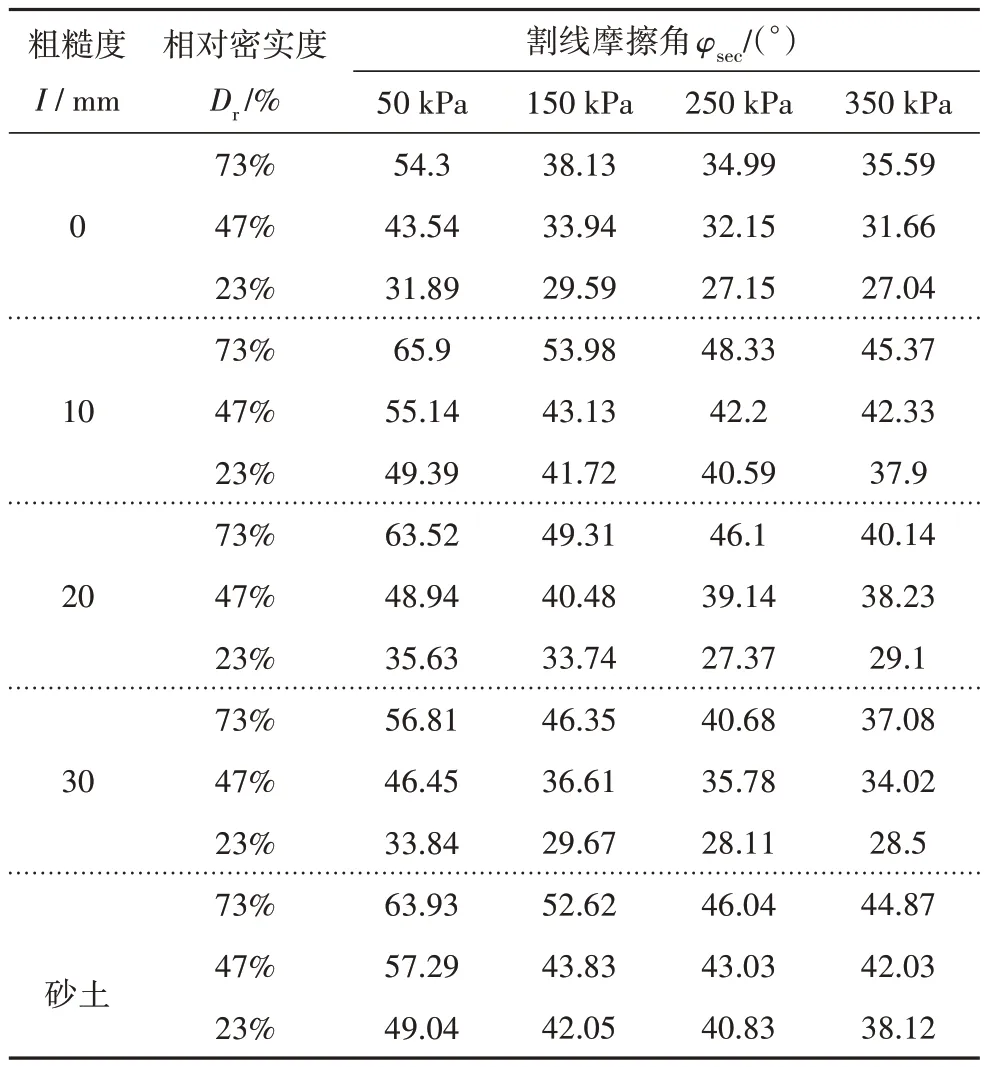

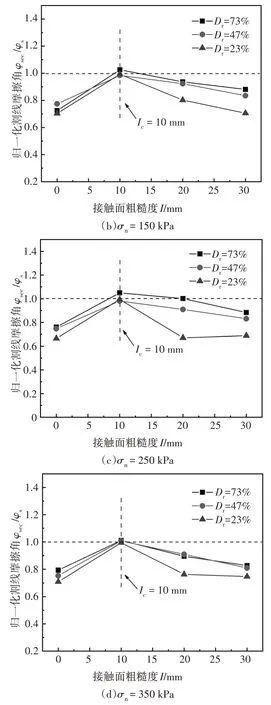
3.4 相对密实度对接触面力学特性的影响
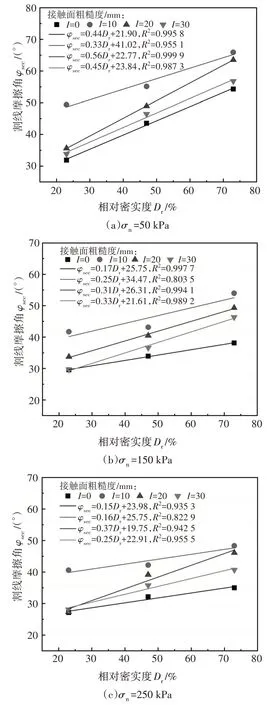


3 结论

