斜坡段桥梁基桩受力与变形分析的传递矩阵法

尹平保，王翱，赵衡，杨铠波，赵明华

［1.长沙理工大学土木工程学院，湖南长沙，410114；2.湖南大学岩土工程研究所，湖南长沙，410082；3.桥梁工程安全控制教育部重点实验室（长沙理工大学），湖南长沙，410114］

在山区修建公路和铁路时，受地形、地貌等水文地质条件的制约，有些路段往往会采用半路半桥或全高架桥的形式来跨越峡谷与河流，因此难免会将桥梁桩基设置在峡谷或河岸斜坡上，而形成斜坡基桩［1］.位于斜坡上的桥梁基桩，其主要承受上部结构传递下来的竖向荷载、水平荷载和偏心弯矩等.但由于基桩前后土体不对称导致的“斜坡效应”，其水平承载特性与常规的平地桩差异显著［2-4］.

为深入分析斜坡段桥梁基桩的水平承载机理及影响规律，赵明华等［5］通过室内模型试验，研究了复杂荷载作用下高陡横坡段桥梁双桩基础的内力与位移变化发展规律及破坏模式；Deendayal 等［6］通过室内模型试验，研究了基桩长径比和斜坡角度的共同作用对桩基承载特性的影响.Sawant等［7］通过有限元数值模拟，分析了水平荷载作用下斜坡坡度变化对桩身弯矩以及位移分布规律的影响.在此基础上，赵明华等［8］和尹平保等［9］综合考虑“P-Δ”效应和桩土相互作用，提出了陡坡段桥梁基桩受力分析的改进有限杆单元法及幂级数法；尹平保等［10-11］基于Mat⁃lock 黏土p-y曲线及双曲线型砂土p-y曲线，推导了斜坡段桥梁基桩内力与位移分析的有限差分解.总体来说，有关斜坡基桩内力与位移计算方法主要有幂级数法、有限差分法和有限杆单元法等［12-15］.其中，我国《公路桥涵地基与基础设计规范》（JTG 3363—2019）［16］主要采用线弹性地基反力法的幂级数通解，即基于m法计算桩身内力与位移，并提供了大量图表以供查询.而以有限杆单元和有限差分为主的数值计算方法，虽然计算精度较高，但其计算过程以及编程均比较复杂，难以在实际工程中推广运用.矩阵传递法［17-18］是国内外近40年来兴起的一种计算方法，其力学概念清晰，能充分考虑桩身截面尺寸变化、土体各向异性以及复杂边界条件等，具有计算精度高，编程简单等优点，便于实际工程的应用.

鉴于此，拟在现有研究基础上，充分分析斜坡段桥梁基桩的水平受荷特点，建立考虑斜坡效应的桩-土相互作用模型及桩身挠曲微分方程；基于m法和传递矩阵法，推导桩身内力与位移分析的理论解答，编制相应的计算程序；再通过试验结果，验证理论解答及计算程序的可靠性；进而分析斜坡坡度和桩顶水平荷载对桩身受力与变形的影响.

1 桩身内力与变形分析的传递矩阵法

1.1 计算模型及挠曲微分方程

实际工程中，斜坡上的桥梁基桩可分为两段：一是桩身位于坡面以上的自由段l0；二是桩身位于坡面以下的入土段lp，如图1所示.

假设桩顶主要承受轴向荷载P0、横向荷载Q0及偏心弯矩M0的共同作用，以桩顶轴心为原点可以建立wO'Z坐标系；再沿桩身纵轴线自上而下依次将桩身划分为N段；其中，自由段分为k段，入土段分为N-k段.在图1所示的计算模型中，以第i微元段桩顶中心为原点，可建立wiOiζi坐标系，见图2.

图1 桩-土相互作用模型Fig.1 Pile-soil interaction model

图2 基桩第i微元段受力分析示意图Fig.2 Force analysis of the micro element section i of the pile

通过对第i微元段进行受力分析，即可建立该微元段的挠曲微分方程：

式中：wi为第i微元段桩身水平位移；ζi为第i微元段计算点到段顶的距离；EiIi为第i微元段桩身抗弯刚度；P0，i为第i微元段顶所受轴向力；b1，i为第i微元段桩的有效计算宽度；qi为第i微元段所在岩土层的水平地基抗力；fi为第i微元段桩身轴力增长系数.

假设桩身自重和桩侧摩阻力沿深度呈线性发展，则桩身轴力增长系数fi的表达式为［14］：

式中：γc，i为第i微元段桩身有效重度；τi为第i微元段对应的桩侧岩土体极限摩阻力，i≤k时，τi=0；Ai和Di分别为第i微元段桩身截面面积和周长.

基于m法假定，第i微元段对应岩土层的水平地基抗力qi可表示为［18］：

式中：m为地基比例系数，当i≤k时，m=0.

将式（2）和式（3）代入式（1）整理可得：

1.2 传递矩阵解答

式（4）可采用幂级数法进行求解，设其解答为：

式中：ηi，0，ηi，1，ηi，2及ηi，3均为待定系数.

根据关系式θi=wi'，Mi=EiIiwi''，Qi=EiIiwi'''+Piwi'与式（5）可得第i微元段的桩身转角θi、弯矩Mi和剪力Qi分别为：

联立式（5）和式（6）消除待定系数ηi，j可得：

式中：wi，0、θi，0、Mi，0及Qi，0分别为第i微元段顶端（ζi=0）的水平位移、转角、弯矩和剪力；Vi为第i微元段的内力与位移传递矩阵，其可表示为：

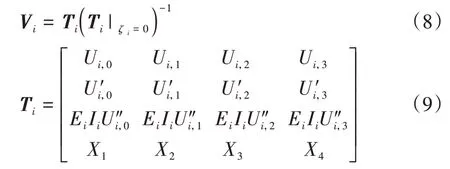
式中：

若第i和i-1微元段桩身内力与位移连续，则有：

根据式（7）和式（11），可得第i微元段与基桩顶端之间内力和位移的传递关系：

式中：Vi-1=Vi-1|ζi-1=li-1；w0、θ0、M0及Q0分别为桩顶水平位移、转角、弯矩及剪力.

对于常规的桥梁桩基，其桩顶边界条件有自由、固定、铰支和弹嵌等；而桩端边界条件有自由、固定等［9，18］，对位于斜坡上的嵌岩桩，通常可假定其桩端边界条件为固定.

若桩顶和桩端边界条件均为自由，则w0、θ0、M0和Q0满足以下关系：

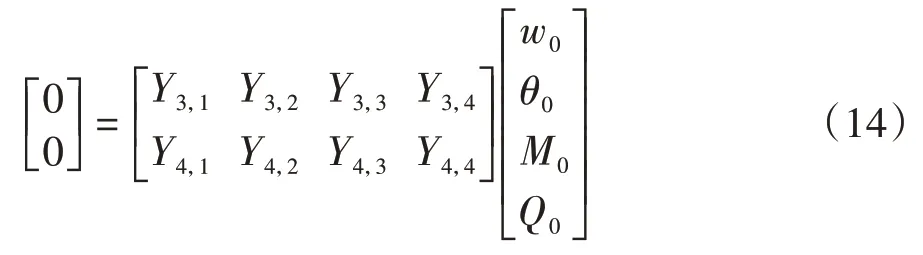
式中：YI，J为矩阵中第I行第J列元素.

式（14）中M0和Q0已知，求解式（14）即可得到w0和θ0.同样地，根据其他边界条件，亦可求解相应的w0和θ0.上述求解过程，均可编程计算.

2 斜坡地基比例系数的试验确定

桩前坡体的存在将导致斜坡地基比例系数与平坦地基有一定差异.虽然我国《公路桥涵地基与基础设计规范》（JTG 3363—2019）［16］中已给出平坦地基比例系数的取值范围，但有关斜坡地基比例系数的确定则缺乏相应的规定或说明.为此，以实际工程中的斜坡基桩为原型，通过室内模型试验测试斜坡地基比例系数，并建立斜坡与平坦地基比例系数间的关系式.

2.1 试验概况

本模型试验主要以湖南省张家界至花垣高速公路泗溪河大桥中某位于斜坡上的桥梁基桩为原型，该基桩总长25.0 m，自由段长7.0 m，入土段长18.0 m，基桩所在边坡坡度约为30°～ 50°.该斜坡地层自上而下依次为：含砾石的粉质黏土（厚约1.0 m），强风化-中风化砂岩（厚约15.0 m），以下为微风化砂岩.本试验采用直径d1=60 mm 的钢管桩测试地基比例系数，而以直径d2=75 mm的PPR管桩测试加载过程中桩身受力与变形.模型桩长度为2 000 mm，自由段和入土段均为1.0 m，桩端嵌入混凝土中0.2 m 以模拟嵌岩.钢管桩身弹性模量Es=1.35 GPa，PPR 管桩身弹性模量Ep=0.37 GPa.模型斜坡填土分为黏土和砂土，其中黏土坡度α=0°、15°、30°及45°，其物理力学参数为：内摩擦角φ=24°，黏聚力c=35.4 kPa，重度γ=18.5 kN/m3，含水率w=15.1%，塑限wP=27.8%，液限wL=45%，曲率系数Cc=3.12，不均匀系数Cu=12.5.而砂土坡度α=0°、30°、45°及60°，其物理力学参数为：内摩擦角φ=39°，含水率w=2.4%，重度γ=15.7 kN/m3，曲率系数Cc=1.05，不均匀系数Cu=8.57.试验用土的级配曲线如图3 所示，具体的模型试验布置如图4所示.

图3 试验用土级配曲线Fig.3 The grading curve of soils

图4 模型试验布置图（单位：cm）Fig.4 Layout of model tests（unit：cm）

2.2 试验加载

试验加载装置由定滑轮、钢丝绳、挂钩和砝码组成.采用慢速维持荷载法分级加载［19］，通过砝码在桩顶施加定向水平荷载，每级荷载为25 N，按0、5 min、15 min、30 min、60 min 的时间间隔采集试验数据.各级荷载稳定标准为变形速率小于0.01 mm/5 min 或累计变形速率小于0.1 mm/h.当某一级荷载作用下坡体开裂严重或桩土交界处位移达到30 mm 时，即可终止加载.

2.3 斜坡地基比例系数mα值的测试原理

如图4 所示，在桩顶逐级施加级水平荷载Q，并用百分表测量水平荷载作用点处桩身水平位移Y1和桩土交界面处桩身水平位移Y2.据此可计算相应坡度下的等效地基比例系数nα值，其计算式为［19］：

式中：H1为水平荷载作用点距桩土交界面的距离；H2为试验桩埋入土体的长度；Q为施加的水平荷载；Y1为水平荷载作用点处桩身水平位移.

斜坡地基比例系数mα与等效地基比例系数nα之间的关系式为：

式中：b1为基桩计算宽度［16］.

2.4 试验结果与分析

通过试验并结合式（15）和式（16），可得斜坡地基比例系数mα与桩土交界面处桩身水平位移Y2之间的关系曲线，如图5和图6所示.Y2=6 mm 时对应的斜坡地基比例系数mα，如表1所示.

表1 实测斜坡地基比例系数mαTab.1 The tested value mα of sloping ground

由图5和和图6可以看出，斜坡地基比例系数mα值随桩土交界面处的桩身水平位移Y2增大而呈非线性关系减小；当桩土交界面处桩身水平位移相同时，斜坡坡度越大，斜坡地基比例系数mα值越小；相对而言，黏土斜坡地基比例系数大于砂土斜坡.

图5 黏土斜坡地基mα-Y2曲线Fig.5 The mα-Y2 curves of clay slope ground

图6 砂土斜坡地基mα-Y2曲线Fig.6 The mα-Y2 curve of sand slope ground

根据表1，经非线性拟合可得斜坡地基比例系数比值λ与斜坡坡度α之间的关系式：

黏土斜坡地基：

砂土斜坡地基：

式中：λ=，mα为斜坡坡度为α的地基比例系数，m0为平地地基比例系数.

斜坡地基比例系数比值λ与斜坡坡度α之间的关系曲线如图7 所示.由图7 可知，斜坡地基比例系数比值λ随斜坡坡度α增加而成非线性关系减小；拟合得到的λ-α关系曲线与实测结果吻合较好.

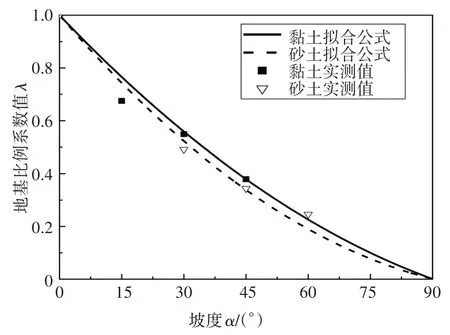
图7 λ-α关系曲线Fig.7 The relation curves of λ-α

3 试验验证及影响因素分析

3.1 试验验证

为验证斜坡基桩内力与位移计算传递矩阵法的合理性，以黏土斜坡模型试验中水平荷载Q0=150 N为例，计算得到不同坡度下桩身水平位移和弯矩随埋深的变化发展规律曲线，其与试验结果的对比如图8和图9所示；地面处桩身水平位移及桩身最大弯矩对比如表2所示.

图8 不同坡度下桩身水平位移曲线Fig.8 Horizontal displacement of piles under different slopes

图9 不同坡度下桩身弯矩曲线Fig.9 Bending moment of piles under different slopes

表2 桩身弯矩与位移计算结果对比Tab.2 Comparison of bending moment and displacement of piles

由图8 和图9 可知，对于黏土斜坡中的模型桩，当试验荷载Q0=150 N 时，不同斜坡坡度条件下实测桩身水平位移和弯矩曲线与计算曲线均吻合较好.另外，表2 显示理论计算得到的桩身最大弯矩和桩土交界面处桩身水平位移结果与试验结果之间的最大误差为8.54%，由此可验证斜坡段桥梁基桩受力与变形分析的传递矩阵法及程序是合理可行的.

3.2 影响因素分析

为进一步探讨斜坡坡度及桩顶水平荷载对桩身内力与位移的影响，以张花高速中某斜坡上的桥梁基桩为例［20］，利用传递矩阵法对其进行影响因素分析.该基桩所在斜坡的坡度约为40º；基桩自由段长为4 m，直径为1.8 m；入土段长度为25 m，直径为2.0 m；桩身混凝土弹性模量Ec=29.6 GPa.桩侧岩土体地基比例系数m=4.0 MN/m4；作用在桩顶的轴向荷载P0=7 312 kN，水平力Q0=50 kN，弯矩M0=520 kN·m.

3.2.1 斜坡坡度的影响

受斜坡效应的影响，斜坡段桥梁基桩的受力与变形与平地桩差异如何尚值得深入探讨.为此，保持其他参数不变，分别计算斜坡坡度α=0°、20°、40°及60°时桩身水平位移和弯矩，其沿深度的变化发展规律曲线如图10和图11所示.

图10 不同坡度下桩身水平位移曲线Fig.10 Pile displacement under different slopes

图10 和图11 显示，在相同的荷载水平下，基桩桩身水平位移和弯矩均随斜坡坡度增加而增大.当斜坡坡度α=0°、20°、40°及60°时，桩顶水平位移分别为2.87 mm、3.22 mm、3.73 mm 及5.35 mm；与α=0°（平地桩）相比，α=20°、40°及60°对应的桩顶水平位移增幅分别为12.2%、30.0%及86.4%.桩身最大弯矩随斜坡坡度增加而有小幅增大，当α=0°时，桩身最大弯矩位置约为坡面以下2.0 m处；而当α=60°时，桩身最大弯矩位置则下移至坡面以下4.0 m 处.由此可见，斜坡坡度增大会使桩顶水平位移显著增加，且对桩身最大弯矩位置有一定影响.这是因为斜坡坡度增大导致桩前浅层土体的水平抗力减弱，促使水平荷载向斜坡深处传递.当以桩身水平位移控制基桩水平承载力时，斜坡基桩的水平承载力将随斜坡坡度增加而减小.

图11 不同坡度下桩身弯矩曲线Fig.11 Bending moment of piles under different slopes

3.2.2 桩顶水平荷载的影响

在实际工程中，风荷载、车辆制动荷载等水平荷载将会通过上部结构传递至桩顶.为探讨水平荷载对斜坡段桥梁基桩内力与桩顶水平位移的影响，假定其他参数相同，分别计算水平荷载Q0=0 kN、50 kN、100 kN 及150 kN 时的桩身水平位移和弯矩，其沿深度的变化发展规律曲线如图12和图13所示.

图13 不同水平荷载下桩身弯矩曲线Fig.13 Bending moment curve of piles under different lateral loads

由图12 和图13 可知，对于斜坡坡度α=40°的斜坡基桩，桩身水平位移和桩身弯矩均随桩顶水平荷载增加而显著增大.当桩顶水平荷载Q0=0 kN、50 kN、100 kN 及150 kN 时，桩顶水平位移分别为2.25 mm、3.73 mm、5.47 mm 及7.29 mm，后者与前者相比，桩顶水平荷载每增加50 kN，对应的桩顶水平位移增幅分别为65.8%、46.6%及33.3%；同样地，当Q0=0 kN、50 kN、100 kN 及150 kN 时，桩身最大弯矩分别为527.6 kN·m、801.0 kN·m、1 170.1 kN·m 及1 484.8 kN·m，也就是说桩顶水平荷载每增加50 kN，对应的桩身最大弯矩增幅分别为51.8%、46.1%、26.9%.由此可见，桩顶水平荷载对斜坡基桩桩身水平位移和最大弯矩的影响更为显著.

4 结论

根据斜坡段桥梁基桩的水平承载特性，建立了考虑斜坡效应的桩-土相互作用模型及桩身挠曲微分方程，推导了基桩受力和变形分析的传递矩阵解答，测试了黏、砂土斜坡地基比例系数，验证了传递矩阵解答的合理性，并开展了相应的影响因素分析.得到的主要结论如下：

1）与传统的有限元法相比，斜坡段桥梁基桩受力和变形分析的传递矩阵法，能充分考虑桩身截面尺寸变化及复杂边界条件，其力学概念清晰、参数少且易获取、无需建模，计算效率高，便于应用.

2）斜坡地基比例系数随桩土交界面处桩身水平位移增大而呈非线性关系减小；桩身水平位移相同时，斜坡坡度越大，斜坡地基比例系数越小；坡度相同时，黏土斜坡地基比例系数大于砂土斜坡.

3）在相同的荷载水平下，斜坡坡度越大，基桩桩身水平位移和弯矩也越大；斜坡坡度由0°增加至60°，其桩顶水平位移约增大86.4%，桩身最大弯矩约增大4.6%，桩身最大弯矩位置约下移2.0 m.

4）斜坡坡度相同时，基桩桩身水平位移和桩身弯矩均随桩顶水平荷载增加而显著增大；桩顶水平荷载每增加50 kN，桩顶水平位移平均增大48.6%，而桩身最大弯矩平均增大41.6%.