基于LabVIEW 的主动磁悬浮轴承位移传感器故障识别

杨昕红，郑安琪

（1.沈阳职业技术学院 人事处，辽宁 沈阳 110045；2.沈阳工业大学，辽宁 沈阳 110870）

1 传感器探头失效的主要形式及仿真方法

磁浮轴承的工作特点决定了其对转子的实时位移需要不间断地测量，以便于调整其位置。电涡流传感器具有结构简单、灵敏度高、无油污染等优点，被广泛应用于工程中的位移测量。同样，也经常用于磁浮轴承的位移测量［1］。工作人员可以通过安装在转子附近的电涡流传感器探头掌握转子的工作状态。但探头处于恶劣的工作环境，在工作过程中容易受到振动和高速气流等干扰。因此，探头是位移传感器最脆弱的部分［2］。

探针故障的种类繁多。依据功能受损程度的不同，可以把传感器探头失效问题划分为部分故障和整体故障：前者意味着探头可以继续工作，但是已经出现一定程度上的功能障碍，如松动和线圈老化等现象［3］；后者意味着探头出现严重问题，已经无法完成检测任务，如线圈短路等现象。传感器探头失效会导致传感器输出异常，若处理不及时，则无法确保磁浮轴承安全可靠地运行。

实际上，在传感器的输出信号中除了转子位置信号以外，还夹杂着无效信号。换一个角度看，可以将此无效信号视为向传感器输入的干扰信号。因此，在建立故障传感器模型时，采用在传感器上叠加干扰信号的方法来模拟探头的故障。

2 磁力轴承工作原理

图1 为单自由度主动磁悬浮轴承（仅考虑转子干涉和探头故障）的示意图。传感器以差分方式测量转子位置［4］。图1 中每个结构的具体说明如表1所示。

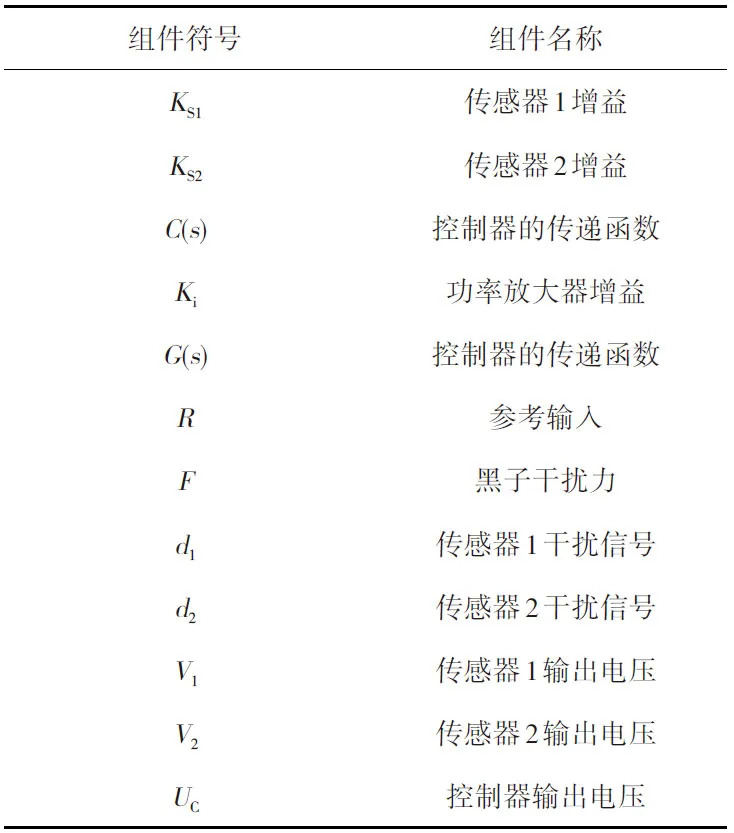
表1 单自由度差动位移传感器磁力轴承结构组件

图1 单自由度差动位移传感器磁力轴承结构

图2 为使用LabVIEW构建的单自由度AMB控制系统仿真模块。PID 调节模块的参数调节方法主要有理论计算法和实验法。本文通过反复调试PID模块参数，观察响应曲线，最终得出最佳参数值。试验结果为P=4.5，积分为100，导数为0.1，Ki=1.04。

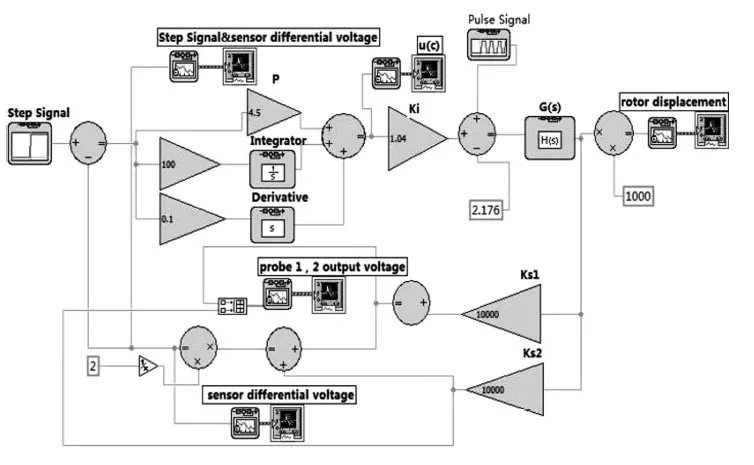
图2 基于LabVIEW 的电磁轴承控制系统仿真模块

PID 控制的仿真结果如图3 所示。在0.5 s 时2 A脉冲信号给出的响应波形如图4 所示。系统参考电压设为2.5 V。

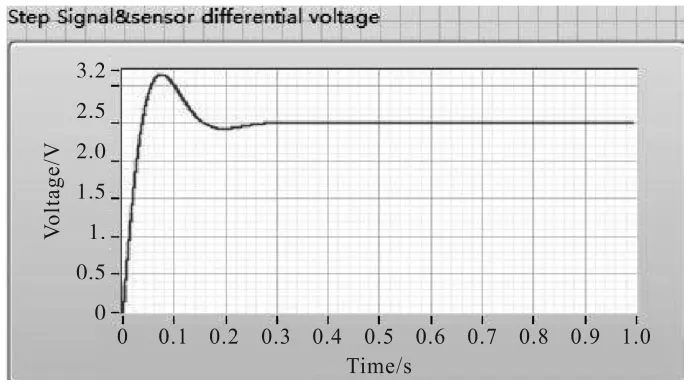
图3 PID 控制仿真结果

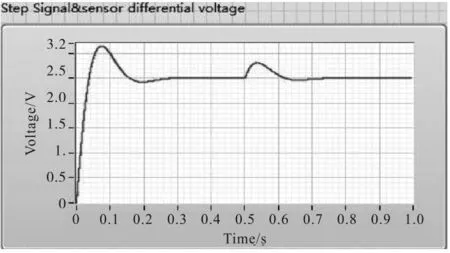
图4 转子冲击响应仿真结果

3 位置传感器故障检测

通过图1 的等效变换得到3 种结构简图，如图5所示。

图5 差模转子位移测量用磁浮轴承的3种结构

由图5a可推得输出与输入之间的关系：

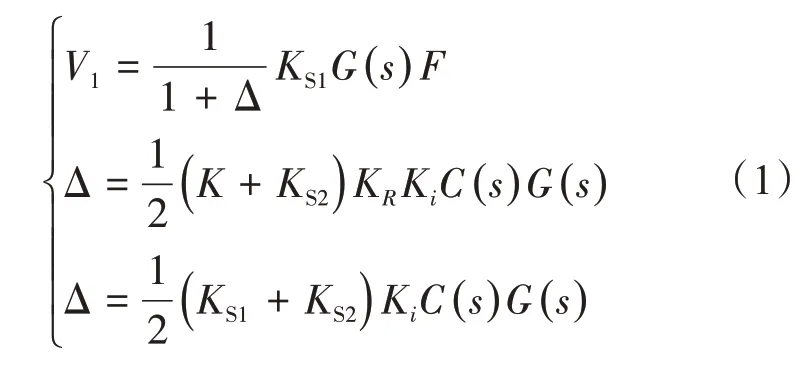
根据图5b之间的传递函数可以得到V1和d1之间的关系：

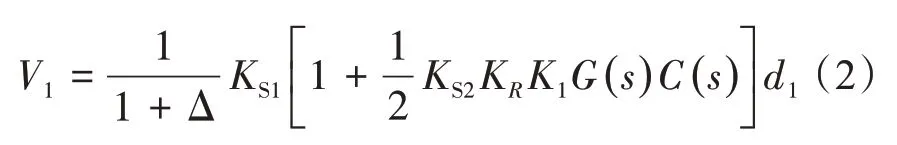
根据图5c之间的传递函数可以得到V1和d2之间的关系：

V2、d1、d2和f的计算方法如下：

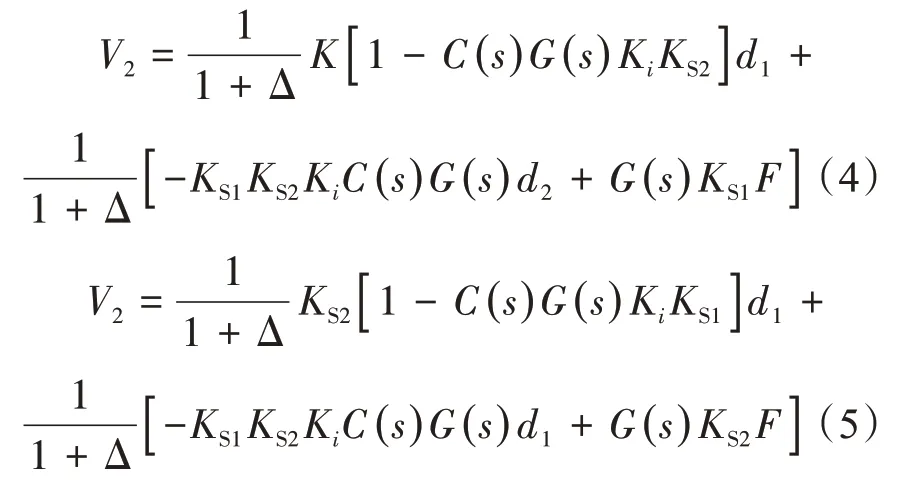
根据式（4）和式（5），可以推断出两个位移传感器输出信号之间的差异：

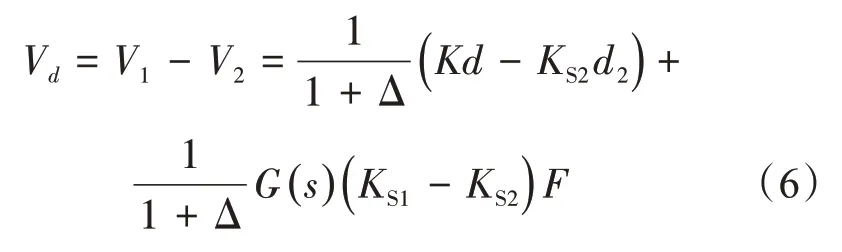
假设两个位移传感器的特性完全相同：

则式（6）可以简化为

由（8）可以看出：当两个传感器的参数一致时，其输出信号的差异仅仅与探头故障相关，这一结论可用于诊断位移传感器的故障。若输出差值不为0，则说明存在探针故障。当然，在实际应用中不存在参数完全一致的两个传感器，因而定义了一个误差阈值Vtol。如果信号之间的差异使两个传感器满足式（9），则表明探针没有故障；反之，探针有故障。

4 基于DFT的故障位移传感器识别

由式（8）可知：这两个探针中的任何一个有错误都会引起Vd发生改变。通过监测Vd可以发现探头故障，但无法识别，必须找到有效的方法来识别发生故障的传感器探头。

4.1 直接判别分析

在正常情况下，传感器的输出信号应在一定范围内；当传感器发生故障时，输出信号将超过正常信号范围。因此，如果位移信号超过正常范围，则可以肯定传感器发生故障。直接判断的优点是检测速度快，缺点是只能识别某些特定的故障［5］。

4.2 离散傅立叶变换（DFT）

只有当传感器的输出信号超过正常范围时，直接判断分析才有效。但如探头松动等故障，只在一定程度上影响输出，不会导致输出超过正常范围。对于这种不完全失效，需使用离散傅里叶变换（DFT）来识别［6］。

由图1 可知，控制器的输出信号、传感器的扰动信号与转子的扰动力的关系如下：

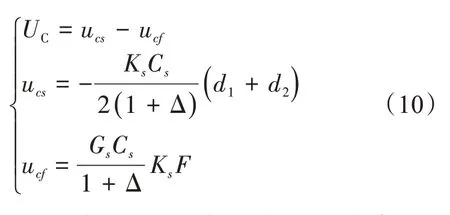
式中，UC包含两个部分：一个部分与探针故障(ucs)有关，另一部分与转子的干涉力(ucf)有关。

假设传感器1失效：

假设传感器2失效：

将式（11）带入到式（10）中，得

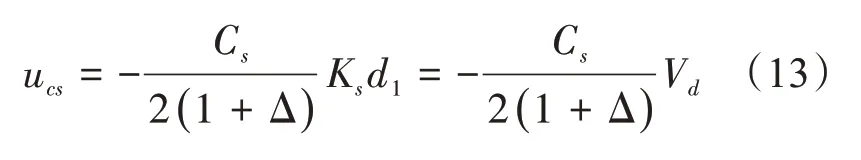
将式（12）带入到式（10）中，得

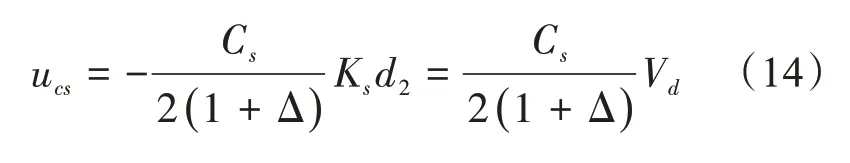
式（13）和式（14）可以统一如下：

如果传感器1失效，ucs和Vd之间的比例系数为负，其相位差为180°；如果传感器2失效，ucs和Vd之间的比例系数为正，其相位差为0°。

5 模拟分析

为了证明上述理论分析的结果，以单自由度主动磁轴承为研究对象，利用LabVIEW 模拟提出的传感器故障识别算法，仿真程序如图6所示。

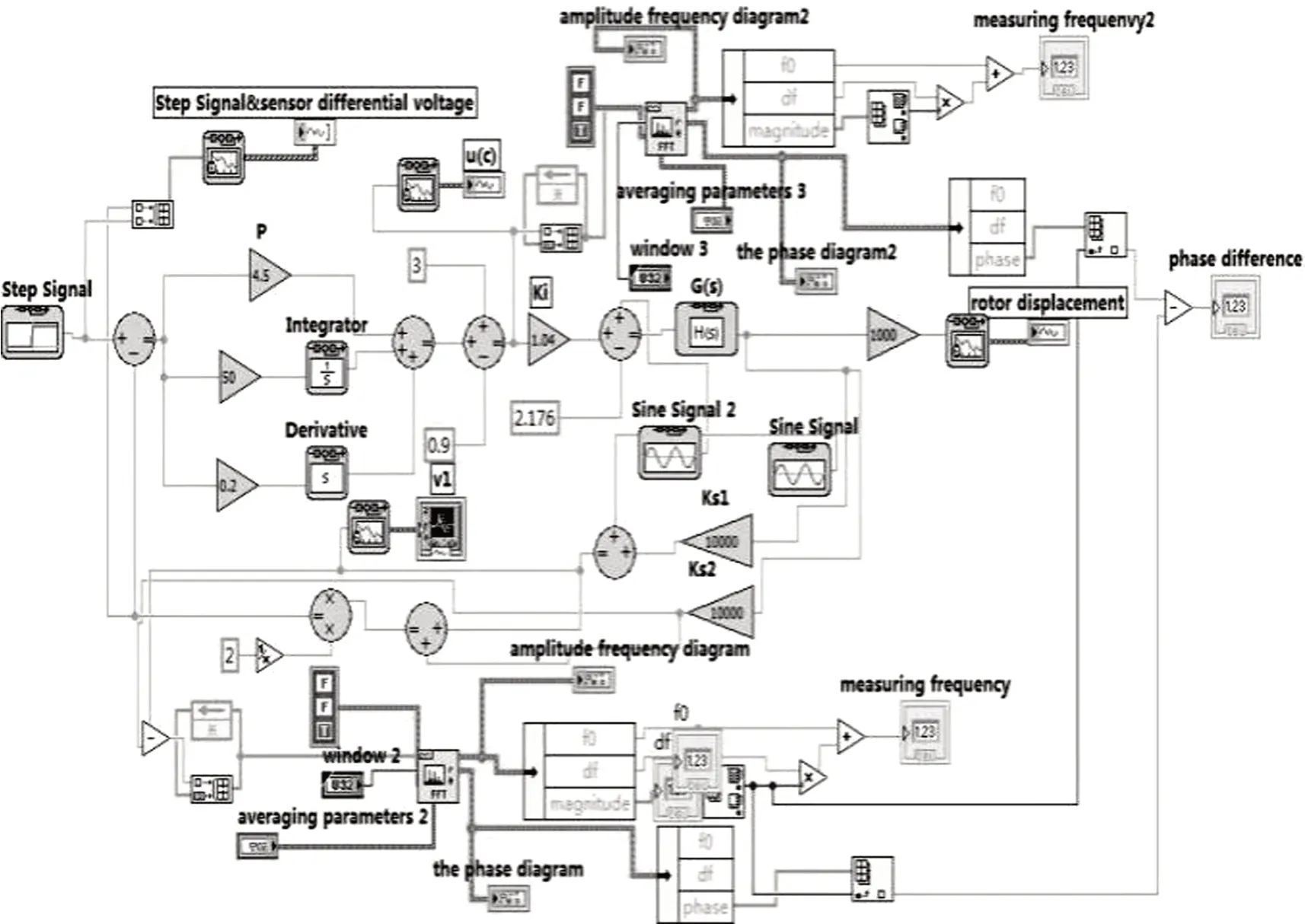
图6 基于LabVIEW 的传感器故障识别算法仿真程序

在图6中，通过在传感器上叠加幅值为2 V，频率为300 Hz 的正弦干扰信号来模拟探头故障。通过在转子上叠加1 A 和100 Hz 的正弦干扰力来模拟转子中的离心力。在模拟开始时，干扰信号叠加在相应的传感器上。

当故障信号叠加到传感器1 时，传感器差分信号的幅度谱控制器输出信号如图7所示。当探针1失效时，传感器差分信号在300 Hz 处产生峰值，可以确定探针故障。同时，控制器输出信号的幅度谱也在相应的错误信号频率产生峰值（如图7b）。图8 为传感器1 故障时，传感器差分信号与控制器输出信号在300 Hz 故障信号频率下的相位差。当传感器1 发生故障时，传感器差分信号与控制器输出信号在300 Hz 时的相位差稳定在180°。仿真结果与理论分析结果一致。

图7 传感器1发生故障时对应的Vd和Uc幅度谱

图8 传感器1发生故障时Vd和Uc在300 Hz下的相位差

当同一故障信号叠加在传感器2 时，传感器差分信号和控制器输出信号的幅度谱如图9 所示。从图7 和图9 可以看出：传感器差分信号和控制器输出信号的频谱完全相同。图10 显示了传感器2在失效状态下且故障信号频率为300 Hz 时，传感器差分信号与控制器输出信号的相位差。

图9 传感器2发生故障时对应的Vd和Uc幅度谱

图10 传感器2发生故障时Vd和Uc在300 Hz下的相位差

如图10 所示，当传感器2 发生故障时，传感器差分信号与控制器输出信号在300 Hz 时的相位差稳定在0°。仿真结果与理论分析结果一致。

6 结论

本文以主动磁轴承为研究对象，采用差动位移传感器检测转子位移，然后根据模型，不仅推导出控制器关于转子干扰和传感器故障信号的传递函数，而且推导出传感器差分信号关于转子干扰力和传感器故障信号的传递函数。通过分析控制器输出信号之间的关系、传感器的差分信号和不同传感器发生故障时的故障信号，得出以下结论：

1）如果两个传感器正常，则传感器之间的差分信号为0；如果其中一个传感器故障，则两个传感器的差分信号将增加。

2）如果传感器1 发生故障，则两个传感器的差分信号与控制器的输出信号在故障频率下的相位差为180°。

3）通过分析两个传感器差分信号的幅值频率特性，可以诊断传感器故障，进而分析两个传感器的差分信号与控制器在干扰频率下的输出信号之间的相位差，以确定哪个传感器失效。为了检验结论是否正确，采用LabVIEW 对传感器故障识别方法进行了仿真。仿真结果表明：该方法能够准确地检测传感器故障，识别故障传感器。