基于海鸥算法的综合能源系统优化规划研究

杨 硕，叶 鹏，刘俐利，王 欢，孙 峰

（1.沈阳工程学院 电力学院，辽宁 沈阳 110136；2.国网辽宁省电力有限公司盘锦供电公司，辽宁 盘锦 124000；3.国网辽宁省电力有限公司电力科学研究院，辽宁 沈阳 110000）

综合能源系统（Integrated Energy System，IES）作为解决当前能源问题的有效手段，具有能源的产生、分配、转换和调度的功能。同时，IES 提高了能源消耗效率，促进了清洁能源的发展和可再生能源的消纳。未来，随着综合能源技术的发展，IES 中的主要能源供应设备的类型将更加多样化，并且特征与传统电力系统不同［1-2］。IES 的规划是一种复杂的非线性、多目标、多约束的混合整数优化问题。为了更好地实现综合能源系统的规划，通常采用现代智能优化算法对系统规划问题进行求解，常用的算法有：遗传算法、禁忌搜索算法和粒子群优化算法等［3-5］。不合理的综合能源系统规划会影响系统的能源利用效率，为了充分发挥IES的作用，需要从整体上对其进行合理的配置。

与传统的独立能源供应模式相比，IES 中包含了更多的能源设备耦合，其能源网络更加复杂。不合理的配置将难以串联整个系统，为了更好地发挥系统的优势，需要对每个设备提前做好规划。关于IES 的规划优化，目前已经有大量学者进行了研究。文献［6］考虑了能源耦合设备类型选择和系统容量配置问题，应用混合整数线性规划算法，对建立的年综合经济性最优模型进行优化规划。文献［7］提出了一种双层的多目标规划模型，引入权重系数以系统的最小化投资成本、运营成本和碳排放最低为目标，上层采用鲸鱼算法进行优化，下层使用MATLAB/YALMIP/GUROBI 联合求解器，得到系统的最佳容量和经济性。文献［8］考虑了建设时序问题对园区综合能源系统规划的影响，基于统一母线模型，综合投资和运维费用，以系统建设的全寿命周期的经济性最优为目标，提出了一种分阶段的规划模型。文献［9］中引入了碳交易机制，对碳排放量进行制约，考虑设备投资和运维费用，采用两阶段鲁棒模型进行优化规划控制。文献［10］中建立了规划-运行两阶段模型，并应用粒子群算法对模型进行优化，得到了耦合单元最佳配置。目前，国内外对IES中规划优化的解算策略的研究普遍过于复杂，面临着求解过程繁琐、易陷入局部收敛的问题，效率较低。此外，缺乏对能源耦合单元的全面分析，针对规划应用所提供的可选择的耦合单元种类较少，大多都是确定的设备策略或应用场景，在给定的基础上进行设备优化。同时，对于能源耦合单元间的耦合程度解释不够，缺少与传统能源间的定量对比，难以准确地评估IES高能源利用率和良好的经济性。

本文以热电联产系统、光伏、地源热泵、燃气锅炉、电锅炉等能源耦合设备为核心，同时配置储能储热设备来灵活地应对系统负荷变化，并建立考虑投资成本、碳排放成本和一次能源消耗的多目标规划模型。本文引入海鸥优化算法［11-13］，该算法具有良好的全局寻优和局部寻优特点，结合IES 内各设备和母线等约束条件，对规划模型进行求解，最终得到系统经济性和环保性指标及耦合单元容量配置和调度方案。与传统的独立能源系统进行比较，以某IES 园区为例，验证算法的准确性，通过经济性和环保性指标证明IES的优势。

1 综合能源系统建模

1.1 典型能源耦合单元模型

1.1.1 热电联产系统

热电联产系统（CHP）将从系统外购买的天然气转化为电能和热能，其模型和运行约束条件为

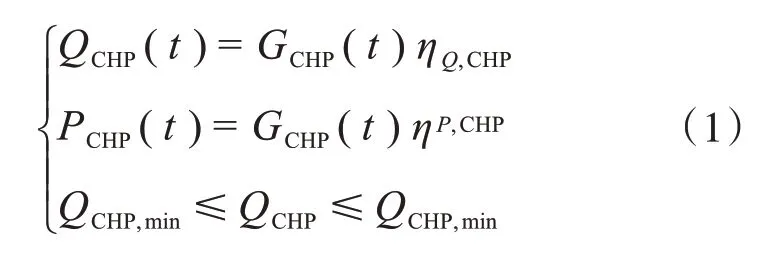
式中，QCHP(t)为在t时刻热电联产系统产生的热功率；PCHP(t)为在t时刻热电联产系统产生的电功率；GCHP(t)为在t时刻热电联产耗费的天然气功率；ηQ,CHP为热电联产机组的产热效率；ηP,CHP为热电联产系统的供电效率；QCHP,min和QCHP,max分别为热电联产系统供热功率的最小值和最大值。

1.1.2 光伏

光伏（PV）的发电功率与众多因素有关，包括光照、温度、设备的运行状态等。假设当光伏采用最大功率点跟踪控制策略时，其模型和约束条件［14］为

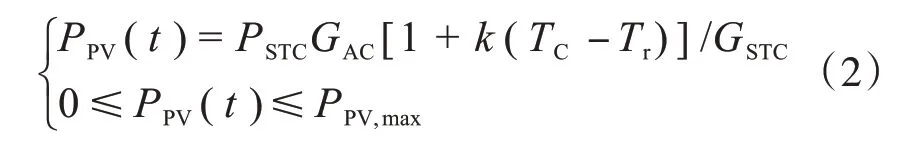
式中，PPV(t)为在t时刻光伏的发电功率；PSTC为在标准实验条件下的发电功率；GAC为光照强度；GSTC为在标准实验条件下的光照；k为温度系数；TC为光伏发电温度；Tr为参考值；PPV,max为光伏最大出力。

1.1.3 地源热泵

地源热泵（HP）作为系统中电热耦合的转换设备，通过耗费电能，将热能从低品质提升到高品质来满足系统热力需求，其模型和约束条件为

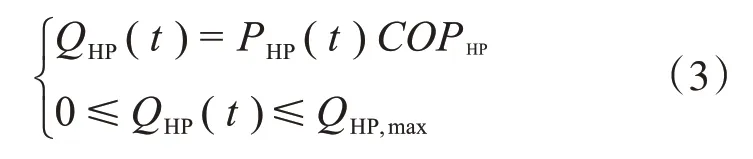
式中，QHP(t)为在t时刻的地源热泵产生的热功率；PHP(t)为在t时刻地源热泵耗费的电功率；COPHP为电热的转换效率；QHP,max为地源热泵供热功率的最大值。

1.1.4 燃气锅炉

燃气锅炉（GB）通过燃烧外部购买的天然气来满足系统热负荷需求，其模型和约束条件为

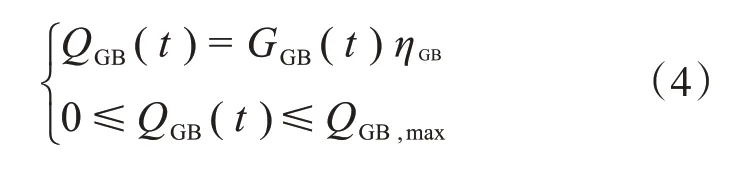
式中，QGB(t)为在t时刻燃气锅炉的产热功率；GGB(t)为在t时刻燃气锅炉耗气量；ηGB为燃气锅炉的效率；QGB,max为燃气锅炉供热功率的最大值。

1.1.5 电锅炉

电锅炉（EB）是系统内电热耦合的关键设备，其效率较高，极大地避免了能源的浪费，其模型和约束条件为

式中，QEB(t)为在t时刻电锅炉的产热功率；PEB(t)为在t时刻电锅炉耗电功率；ηEB为电锅炉的效率；QEB,max为电锅炉的产热功率的最大值。

1.1.6 储能装置

本文设计电储能（ES）和热储能（HS）装置来更好地提高能源的利用率，电储能和热储能的储能机理相似，均需满足如下约束条件［15-16］：

式中，P储能和P放能为单位时间段内设备的储放能功率；P储能,max和P放能,max分别为储能功率最大值和放能功率最大值；W容量为设备容量；η储能和η放能分别为设备储能和放能效率；SOC(t)为在t时刻装置的荷电状态；SOCmax和SOCmin分别为设备的荷电状态的最大值和最小值；SOC(0)和SOC(T)分别为储能设备的运行初始和结束时的荷电状态。

电储能模型为

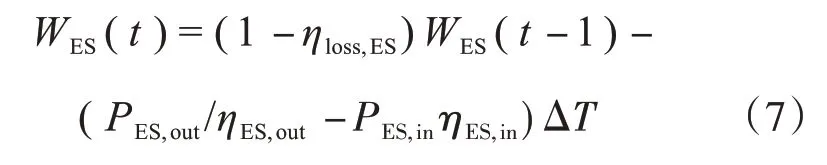
式中，WES(t)和WES(t-1)分别为t和t-1时刻储电装置的容量；ηloss,ES为设备自放电损耗率；ηES,in和ηES,out分别为充电和放电效率；PES,in和PES,out分别为设备的充电和放电功率。

热储能模型为

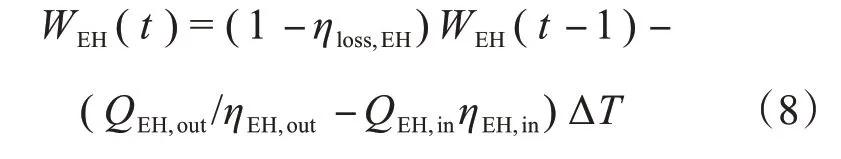
式中，WEH(t)和WEH(t-1)分别为t和t-1 时刻储热装置容量；ηloss,EH为设备自散热损耗率；ηEH,in和ηEH,out分别为充热和放热效率；QEH,in和QEH,out分别为设备的充热和放热功率。

1.2 基于统一母线的综合能源系统模型

在确定了综合能源系统各耦合单元模型的基础上，为了更形象地描述各部分的耦合关系，采用统一母线的建模理论［17］，对综合能源系统整体建模，如图1所示。考虑综合能源系统实际情况的同时，根据耦合设备类型建立了包括电母线、天然气母线和热母线，并规定了3条母线的功率约束条件。

图1 综合能源系统统一母线式结构模型

1）电母线功率平衡约束

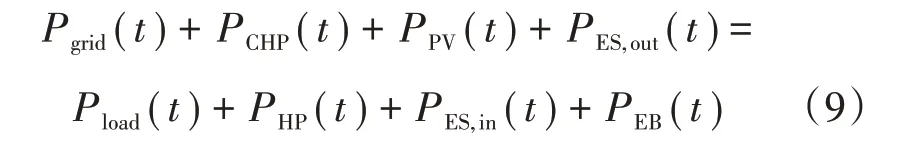
式中，Pgrid(t)为在t时刻外部电网输入的电功率；PES,in(t)和PES,out(t)分别为在t时刻电储能设备的充电和放电功率；Pload(t)为在t时刻系统的电负荷需求功率。

2）热母线功率平衡约束

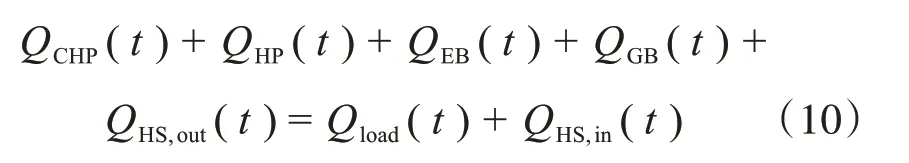
式中，QHS,in(t)和QHS,out(t)分别为在t时刻储热装置的充热和放热功率；Qload(t)为在t时刻系统的热负荷需求功率。

3）天然气母线功率平衡约束

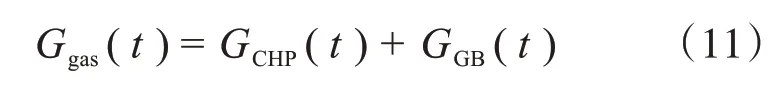
式中，Ggas(t)为在t时刻系统从外部购买的天然气功率。

2 综合能源系统规划模型

2.1 目标函数

综合考虑系统内的热、电、气耦合设备配置，本文提出了一种多目标规划模型，结合不同的热、电负荷比率及系统的全寿命周期运行条件，以年投资最小、CO2排放量最低和一次能源耗费值最小为目标，建立了多目标的规划优化函数，通过优化算法求解并确定各耦合单元的容量。

1）目标函数1：年投资成本（Ycost）

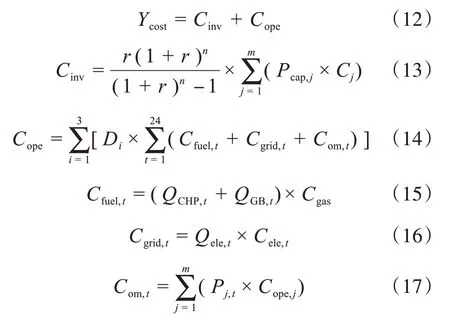
式中，Cinv是设备的初始投资等价成本；Pcap,j是第j个设备的额定容量；Cj是第j个设备每单位容量的初始投资成本；r为折现率；n为使用寿命；Di是第i个典型日持续时间的数量；Cfuel,t是系统耗费燃料的费用；Cgrid,t是系统向外部购电的费用；Com,t是系统运行和维护的总成本；QCHP,t是热电联产系统产生的热量；QGB,t是燃气锅炉产生的热量；Pj,t是第j个设备所消耗的能量；Cgas是系统消耗天然气转换成电能的燃料费用；Cele,t是用电设备的电网用电量；Cope,j是第j个设备的运行和维护成本。

2）目标函数2：CO2排放（YCO2）

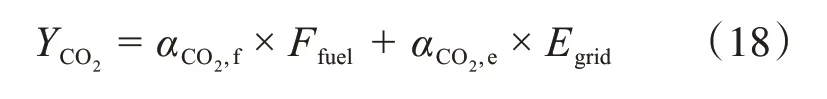
式中，αCO2,f是天然气排放系数；Ffuel是系统消耗的天然气总量；αCO2,e是来自电网的功率耗散因数；Egrid是提供给电网的电量。

3）目标函数3：一次能源消耗（YPEC）

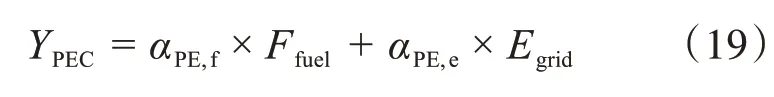
式中，αPE,f表示天然气的一次能源转换因子；αPE,e表示电网的一次能源转换因子。

引入权重将多目标规划优化问题转化为单个综合目标函数的求解，目标函数表述如下：

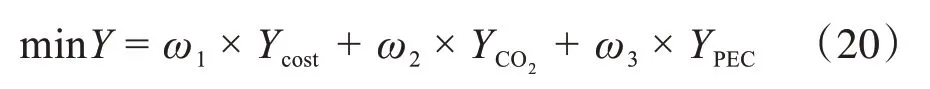
式中，ω1、ω2、ω3为目标的权重，均为1/3。

2.2 约束条件

1）功率约束平衡

整体上需要满足各条母线的功率平衡约束，如式（9）、式（10）、式（11）。

2）设备运行约束

各设备需要满足各自的运行约束，如式（1）～式（6）。

3）外部购能约束

综合能源系统存在从外部购买电能和天然气的情况，需满足如下约束：

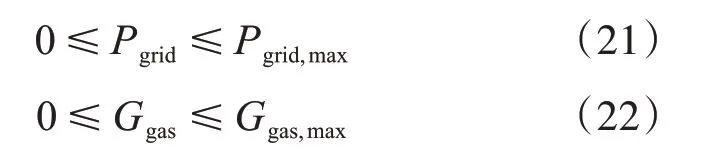
式中，Pgrid,max表示系统向外部购买电能的最大值；Ggas,max表示系统向外部购买天然气的最大值。

3 海鸥优化算法及解算策略

迁徙和攻击行为是海鸥最重要的特征。迁徙是海鸥从一个地方到另一个地方的季节性运动，通过寻找丰富的食物来获取能量。在迁徙期间，海鸥都是成群成组飞行，为了避免彼此之间的碰撞，海鸥的初始位置是不同的。在一个组群里，海鸥不断变动位置，朝着位置最佳的海鸥方向飞行。当海鸥迁徙时，海鸥群体在进攻时会做出自然的螺旋状运动来捕猎鱼虾等食物。这两种行为的表述如图2所示，分别对应了算法的全局搜索能力和局部搜索能力，结合算法与规划模型的对应关系，采用海鸥优化算法对规划模型进行求解。

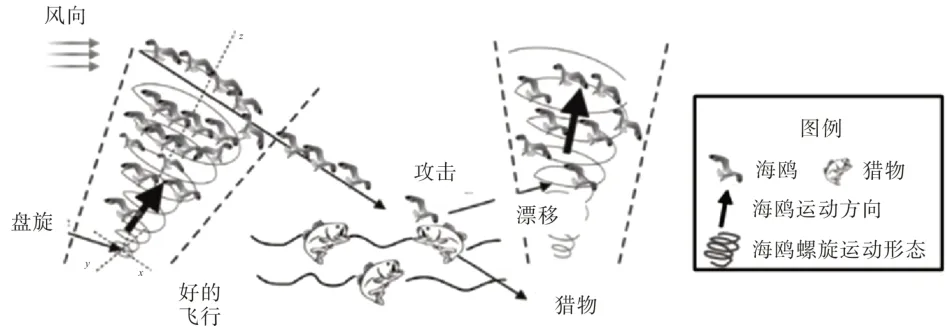
图2 海鸥迁徙和攻击方式

3.1 迁徙（全局搜索）

该算法模拟了海鸥种群的迁徙过程，在这一过程中，海鸥需满足一些条件。

3.1.1 避免碰撞

引入变量A，规避海鸥种群中每个海鸥个体间的相互碰撞，如图3所示。计算新的搜索代理位置：

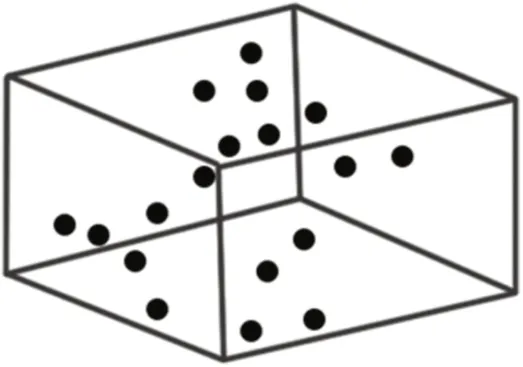
图3 避免碰撞

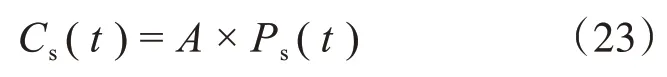
式中，Cs(t)表示不与其余搜索代理冲突的搜索代理的位置；Ps(t)表示搜索代理的当前位置；t表示当前迭代，也表示给定搜索空间的搜索代理的运动行为。

引入fc来控制变量A的频率，使得A从2 呈线性下降到0，用Maxiteration表示迭代的最大次数，即

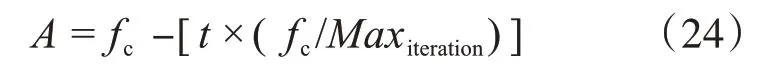
3.1.2 朝最佳位置方向移动

在避免与相邻海鸥之间的碰撞冲突后，搜索代理便朝着最佳位置的方向移动，如图4 所示。表达式为

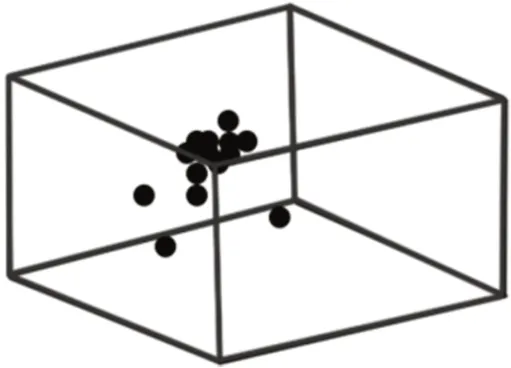
图4 朝最佳位置方向移动

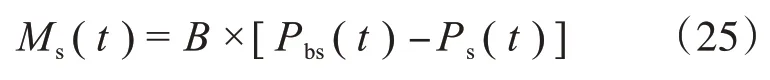
式中，Ms(t)表示最佳位置的方向；Pbs(t)表示最适合海鸥的最佳位置；B是随机数，用来平衡局部和全局的关系。

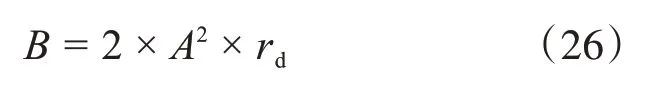
式中，rd为0到1内的随机数。

3.1.3 靠近最佳位置

海鸥移动到不与其他海鸥冲突的位置后，便向最佳位置方向飞行，从而抵达新的位置，如图5 所示。表达式为

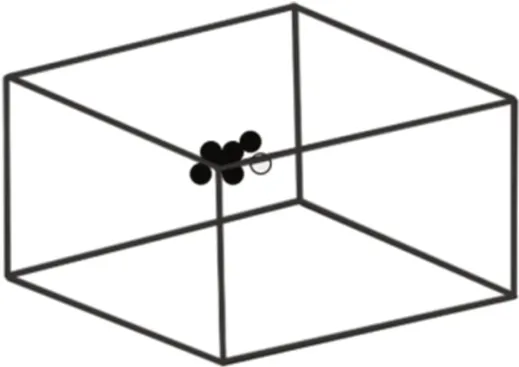
图5 靠近最佳位置

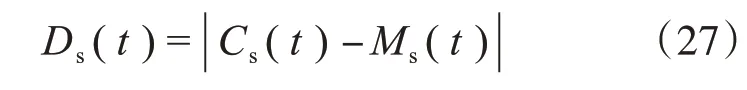
式中，Ds(t)是海鸥的新位置。

3.2 攻击（局部搜索）

海鸥在迁徙过程中通过翅膀的运动和身体重量之间的关系来保持攻击的最佳高度。当发现猎物时，海鸥通过不断地改变攻击角度和速度，以螺旋状的运动方式攻击猎物，轨迹如图6 所示。三维平面（x，y，z）中的运动行为表述如下：

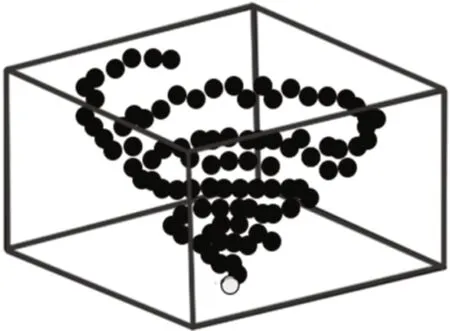
图6 海鸥攻击位置

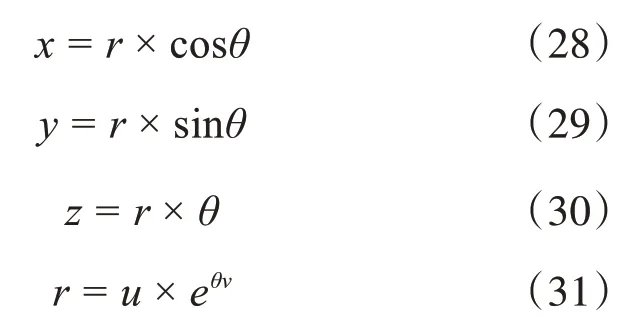
式中，r表示每个螺旋的半径；θ随机取0～2π中的角度；u和v为常数。

经计算可得到海鸥的攻击位置为

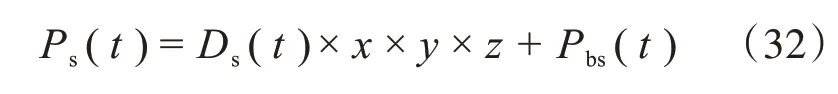
式中，Ps(t)是海鸥的攻击位置。

3.3 求解过程

上述的目标函数属于非线性混合整数问题，用海鸥优化算法进行求解，主要过程如下：

1）对算法中的参数A、B、Maxiteration、u、fc和v进行设置；

2）海鸥种群初始化；

3）若t＜Maxiteration；

4）使用适应度函数计算每只海鸥的适应度值；

5）rd取（0，1）中的随机数；

6）θ取［0，2π］中的随机数；

7）使用公式计算Ds和海鸥新位置Ps；

8）更新最佳海鸥位置和适应值；

9）得到最佳海鸥位置，并输出适应值，结束程序。

在综合能源系统规划模型中，海鸥迁徙过程中的最佳位置对应了目标函数的最优解，海鸥攻击猎物时的角度和速度对应着求解过程中各综合能源系统的合理配置容量，每个海鸥迁徙的最佳位置代表了优化问题中的每个可能解，海鸥迁徙时所处的最佳位置与所求的目标函数的最优解相对应。

4 算例分析

本文以中国北方的某工业园区为例，其中各种能源需求集中，主要为电负荷需求、热负荷需求和气负荷需求。园区规划的基本参数如下：天然气价为2.45 元/m3；电价分别为0.336 9元/（kW·h）（t=1 h～6 h）、1.193 3 元/（kW·h）（t=7 h～18 h）和0.752 5 元/（kW·h）（t=19 h～24 h）；光伏发电的补贴价格为0.42 元/（kW·h）；αPE,f为2.162 2 kg/（kW·h），αPE,e为0.997 kg/（kW·h）；工业园区的电力和热负荷峰值负荷分别为6 300 kW 和7 850 kW。典型日电热负荷需求如图7 所示。系统能源耦合设备费用信息如表1所示。

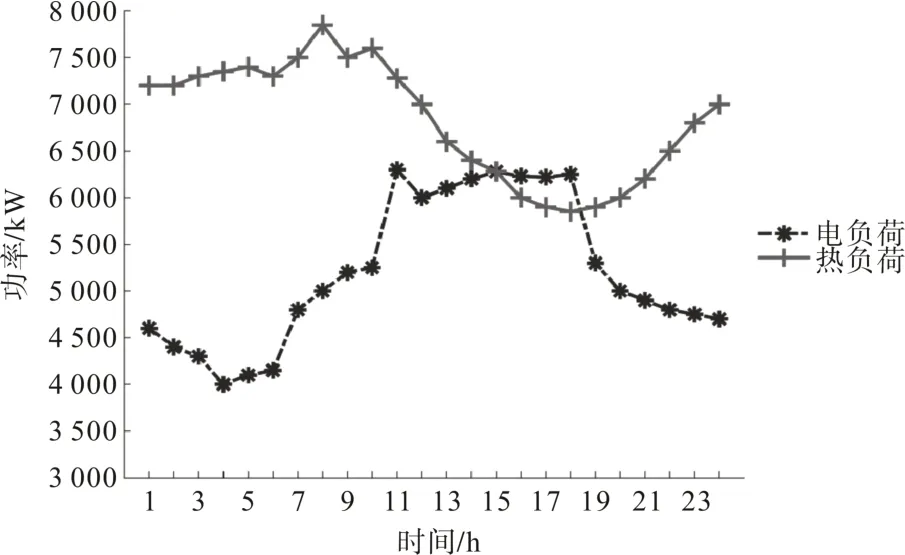
图7 典型日负荷需求

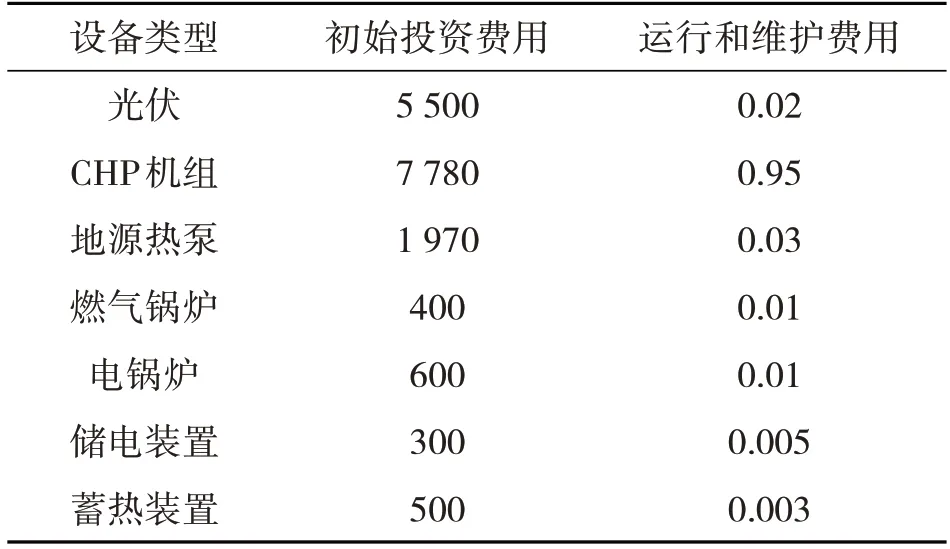
表1 设备费用 元/（kW·h）

经过多次迭代优化，目标函数的最优解为1.452×107。

4.1 各耦合单元容量配置

根据最佳结果分析，容量配置如表2所示。

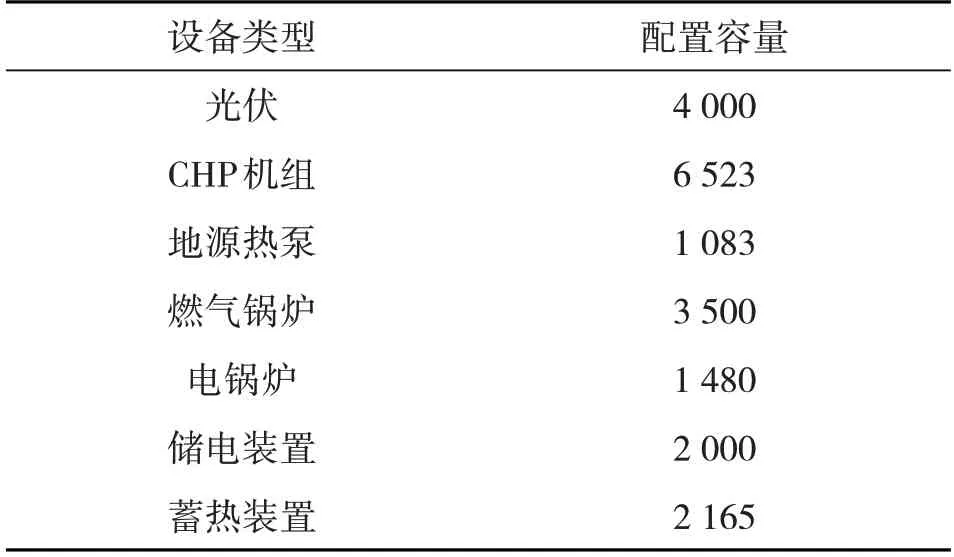
表2 最佳容量配置 kW

4.2 与传统能源供应模式相比较

传统的独立能源供应模式为电能仅从电网中购买，而热能则由燃气锅炉提供。表3 显示了IES中的多能源耦合供应模式与传统独立能源供应模式之间的经济性比较。

表3 IES与传统能源供应模式比较

由表3 可以看出：与传统的独立能源供应模式相比，IES 减少了60.41%的年度成本以及82.27%的CO2排放量。通过对比表明：IES 有效改善了系统内的能源结构，提高了能源的利用率，系统具有更好的经济和环保优势。

4.3 设备调度结果

图8和图9分别显示了典型日的电负荷和热负荷供给和设备调度情况。CHP 机组和光伏发电提供了绝大部分的电力来满足负荷需求，而当电网电价较低时，系统向外部电网采购一部分电能。热力负荷由系统内的热电联产系统、地源热泵、电锅炉和燃气锅炉联合承担。储电和蓄热装置的存储过程平衡了电负荷和热负荷的需求，具有“移位峰谷”的特点。这种能量供应结构将缓解电负载和天然气负载的峰值需求，提高了系统的经济性和可靠性。

图8 典型日电力调度

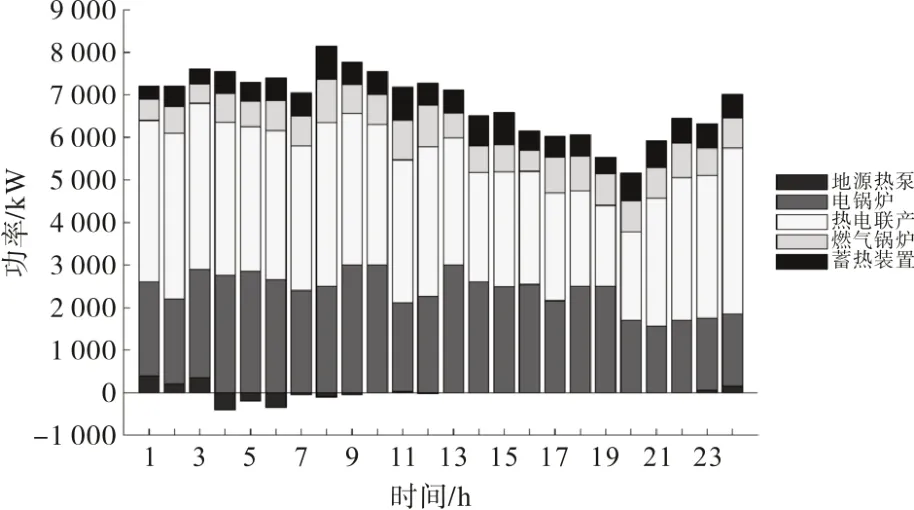
图9 典型日热负荷调度

5 结论

本文提出了一种基于海鸥优化算法综合能源系统的规划方法。海鸥算法作为一种新兴的算法，通过模拟自然界中海鸥的迁徙和攻击行为，使其具有较强的全局搜索和局部搜索能力，对建立的包括年投资成本最小、CO2排放量最低和一次能源消耗最低的多目标函数进行求解，同时考虑了多能源耦合、设备容量、购能等一系列的约束条件。算例结果表明：海鸥优化算法参数设置简单，不需要对结果再次优化，应用于综合能源系统优化中节省了时间，提高了求解效率，优化后的IES 充分发挥了电、气、热多能源和多能源设备间的耦合优势，与传统的独立能源供应模式相比，IES 的能源利用效率得到了显著提高，拥有十分明显的经济和环保优势。