伺服机构故障下运载火箭自适应重构方法

胡存明，张卫东，张桃源，张晓东，王鹏

（1.上海航天控制技术研究所，上海 201109；2.上海航天技术研究院，上海 201109）

0 引言

新一代捆绑运载火箭采用模块化设计，其芯级发动机和助推发动机一起参与姿态控制［1-2］，以提高控制能力，但这也导致伺服机构数量增加、故障概率增大。为了保证运载火箭安全可靠飞行，进一步提高故障情况下的适应能力，亟需开展针对伺服机构故障的高可靠冗余重构控制方法研究［3］。控制重构方法是伺服机构故障重构控制的关键点。常见的重构方法可归纳为非优化分配方法和优化分配方法。非优化分配方法主要包括：按比例系数分配、按指令需求分配、链式递增法分配［4-5］等。优化分配方法主要包括，伪逆法［6-8］、线性规划法［9-11］以及二次规划法［12］等。

目前，重构飞行控制主要以飞机为研究对象［13-14］，运载火箭重构控制研究刚刚起步。冯昊等［15］采用离线控制策略，基于控制力矩不变原则对运载火箭伺服机构卡死故障进行了重构，离线控制策略需要装订大量数据，适应性较差。BODSON［16］提出了迭代伪逆法，但当期望目标不可达时易引起较大平均误差，不适于在线控制分配。程堂明等［17］将伺服机构故障下的摆角分配问题转化为1 范数单目标约束优化问题，采用线性规划方法实现姿控重构。PETERSON等［18］认为针对考虑约束的二次规划最优求解，收敛速率慢，不适用于实时控制。黄盘兴等［19］针对重型运载火箭，考虑位置饱和约束限制，提出了一种伪逆法和不动点法相结合的混合优化控制策略。

本文针对运载火箭伺服机构故障带来的控制重构问题，提出一种计算效率高、误差小的自适应重构方法，给出完整推导过程，通过了数学仿真验证。

1 捆绑火箭动力学模型

以某捆绑运载火箭为研究对象，该火箭配置4 台助推器，各助推器配置单台发动机，芯级配置1 台发动机，芯级与助推发动机推力和最大摆角均相同。发动机和伺服机构布局示意如图1 所示。

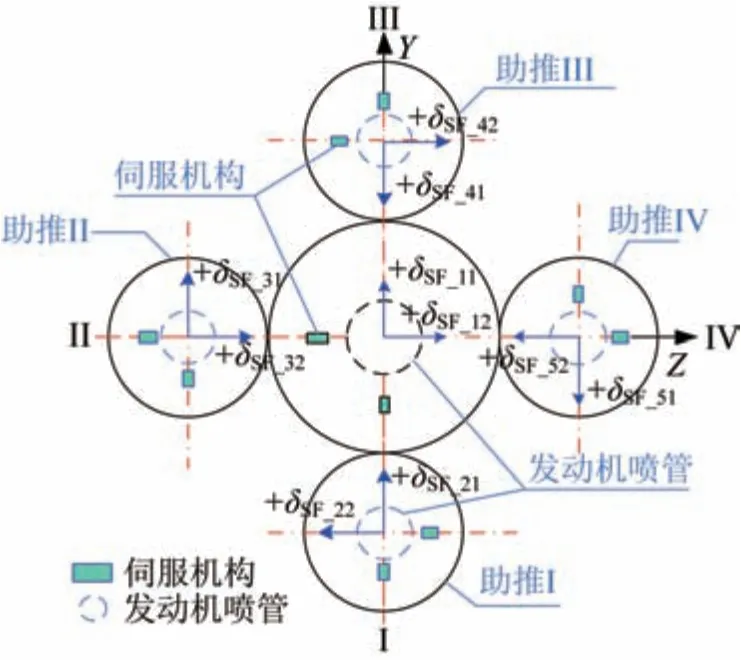
图1 某捆绑火箭发动机和伺服机构布局示意Fig.1 Layout of the engines and servo mechanisms of a launch vehicle

为考核伺服机构故障对姿态控制系统影响，需将伺服机构加入闭环控制，建立伺服机构与等效摆角关系。完整的闭环控制流程框如图2 所示。

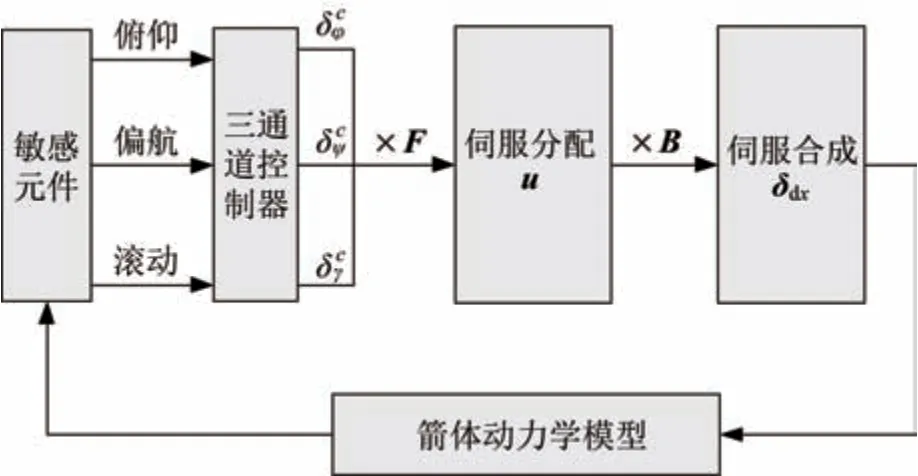
图2 运载火箭控制分配及合成控制流程框Fig.2 Flow chart of the control allocation and synthesis of a launch vehicle

基于发动机和伺服机构布局，建立考虑发动机振动方程的箭体动力学模型，在此只描述伺服故障重构所用模型。

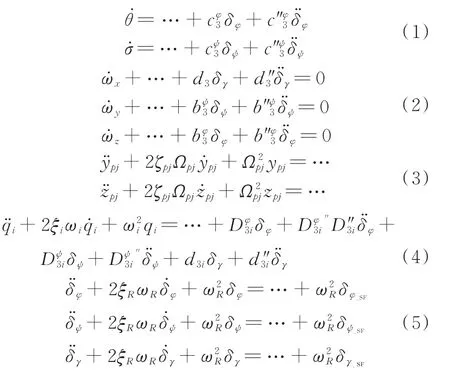
式中：φ、ψ、γ分别为俯仰、偏航、滚动姿态角偏差；ωz、ωy、ωx分别为俯仰、偏航、滚动角速率；θ、σ分别为弹道倾角、弹道偏角；δφ、δψ、δγ分别为三通道发动机合成等效摆角；δφ_SF、δψ_SF、δγ_SF分别为三通道伺服合成等效摆角；Ωpj、ζpj分别为晃动频率和阻尼比；ypj、Zpj分别为贮箱等效晃动质量位移；ωi、ξi、qi分别为火箭第i阶空间模态对应的频率、阻尼比和广义坐标；ωR、ξR分别为发动机频率和阻尼比；分别为刚体运动方程系数。未说明的模型符号的含义参见文献［20］。

针对上述动力学模型，定义状态量x和控制输入u，建立其状态空间模型。

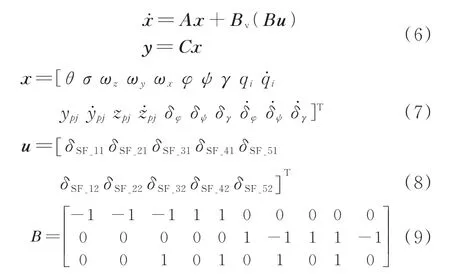
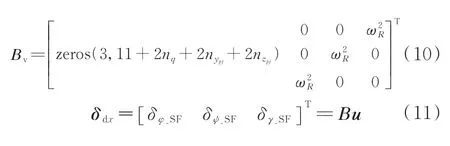
2 控制重构方法研究

基于运载火箭姿态控制模型，开展针对伺服机构故障控制中重构方法的研究。系统可控性要求故障后系统对箭体仍具有一定的控制能力，完成规定任务。控制重构方法中使用到的优化算法主要包括伪逆法、线性规划法、混合优化法。

2.1 基于SVD 改进的控制重构方法

假设rank(B)=r，控制分配模型为f(u)=Bu=Pδ=δf，定义摆角δ和矩阵系数P，控制矩阵B的奇异值分解（Singular Value Decomposition，SVD）为

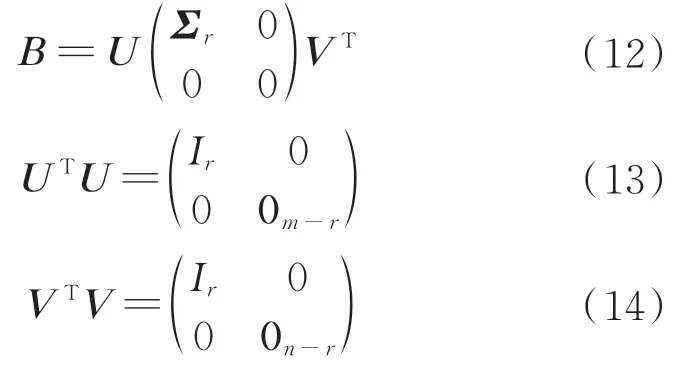
式中：U=(Ur Um-r)；V=(Vr Vn-r)；Σr为单位阵。

建立目标函数：

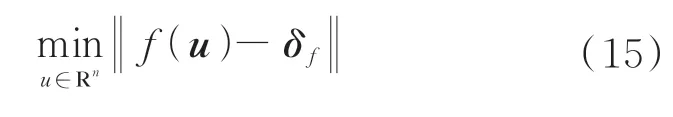
得到：

求取其无穷范数，可得：

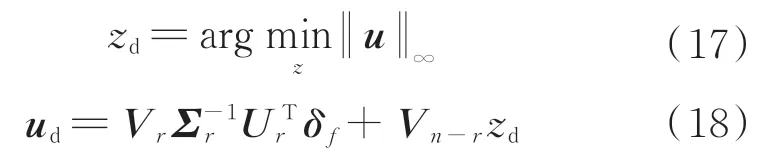
可得到最终的操纵输入：

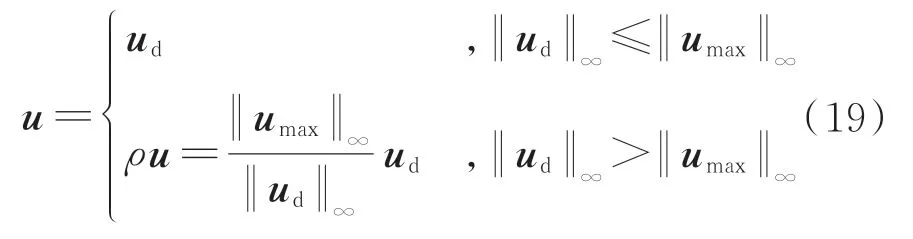
式中：ρ为比例缩放因子。

可以看出ud无穷范数的最小化保证了ρ的最大化，使得式（6）中：

为满足约束的共线最优解，等价于线性规划解。由于最小化无穷范数在实际情况中不便于使用，需近似处理。注意到：

又因为

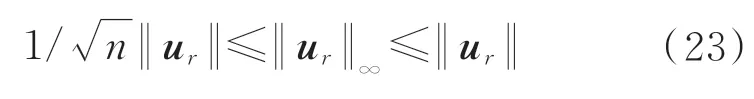
因此当n较小时，可用‖ur‖∞来近似最小化无穷范数，近似误差随n减小而减小。又

在火箭的控制重构中，一般有n≫m，假设r=m，此时：

就是无约束伪逆法的最优解。最终输入为

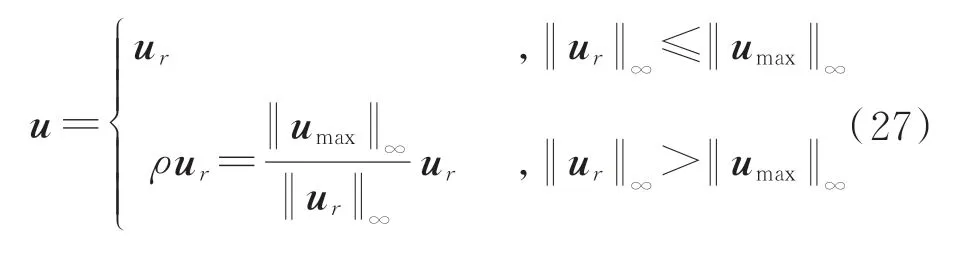
2.2 方法对比分析

针对自变量带约束的f(u)=Pδ问题，当Pδ1在可行集时，能找到u1满足f(u1)=Pδ1，当Pδ2在非可行集时，只能通过优化算法求解。以自变量约束在自由度xn，xn+1上形成的可行集边界为例，3 种常用优化算法差异对比如图3 所示。

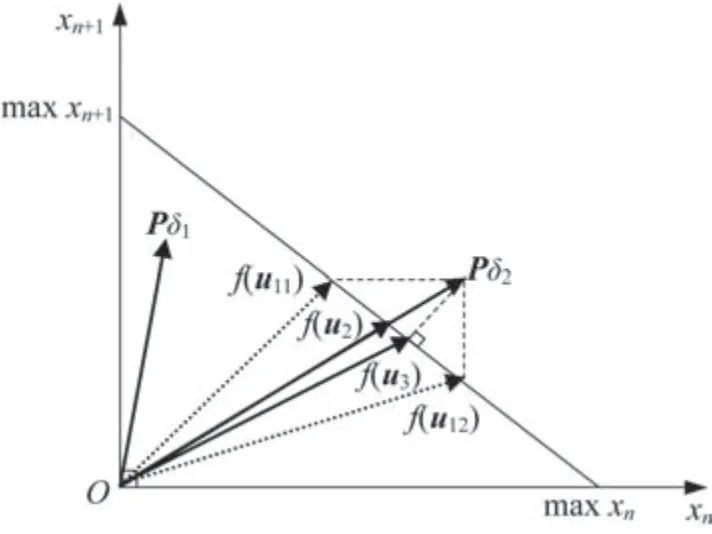
图3 控制重构优化算法对比Fig.3 Comparison of several control reconfiguration optimization algorithms

伪逆法极小化输入范数，但是不能充分考虑输入约束，常用的对输入直接截断方法虽然高效，但是会造成部分通道丧失控制能力。带截断的伪逆法在图3 中的优化结果为f(u11)到f(u12)的扇形区域，最终的值取决于xn，xn+1对截断输入的依赖程度。

线性规划法在Pδ2矢量方向寻找误差范数最小的解，最优解为目标矢量方向与对应可行集边界的交点，如图3 所示。因为线性规划法保证了优化结果与目标矢量方向相同，适用于产生目标力和目标力矩的应用场合。

混合优化法综合考虑了输入需求和输出误差范数。通过加权值改变输入代价和输出误差代价的权重，其可退化为伪逆法和误差最小法。误差最小法的优化目标为误差范数最小，最优解为目标矢量与可行集边界最近的点，即Pδ2在边界的垂线交点f(u3)。误差最小法适用于距离误差需求优于方向误差的应用场合。

伪逆法便于实现，复杂计算可离线实现，但会造成控制耦合问题；而线性规划法虽然优化输出始终保持与目标等效摆角矢量共线，但需要实时进行在线线性规划求解，对系统计算能力要求较高，且输入易饱和；混合优化法存在收敛问题和控制耦合问题。本文针对现有方法存在的缺点，提出了一种基于SVD 改进的控制重构方法。

基于SVD 的改进算法优化目标与线性规划法相同，在输入无约束情况下计算输入解集，通过最小化解集元素的无穷范数得到初始解，初始解是最有可能满足输入约束的解。若初始解u*满足输入约束，则直接得到最终输入为u*；否则，通过比例缩放因子ρ，使得输入u4=ρu*满足约束边界条件，同时由于：

保证了u4为满足共线输出特性的最优解，等价于线性规划解。改进方法与线性规划法优化结果对比如图4 所示。

图4 中：f(u42)=f(u2)为线性规划算法得到的最优解，也是改进方法得到次优解的上边界，f(u41)=为改进方法得到次优解的下边界，出现下边界的必要条件为

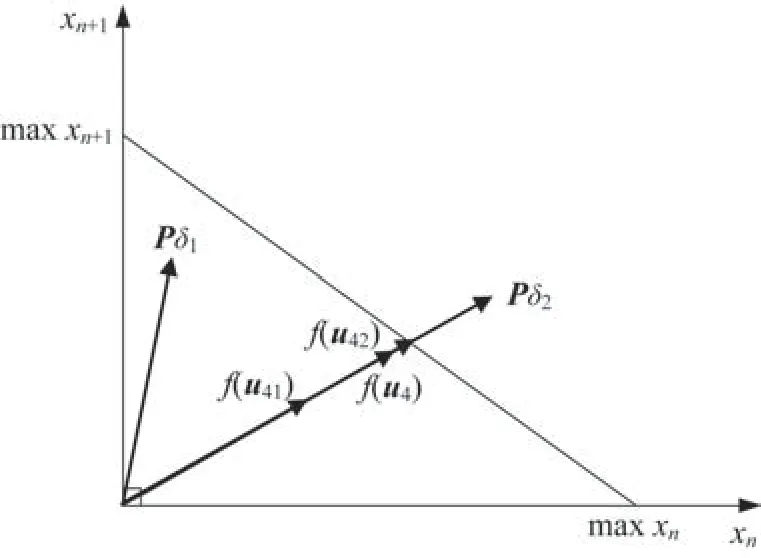
图4 基于SVD 改进的控制重构算法优化结果Fig.4 Optimization results of the improved control reconstruction algorithms based on SVD

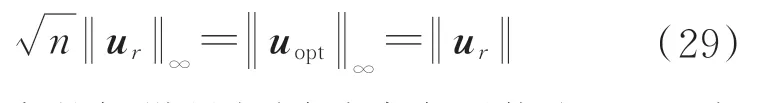
即当所有的操纵量相同时才有可能出现，而在实际情况中优化得到的操纵量通常集中在几个伺服机构。

3 仿真与分析

3.1 性能对比分析

基于伪逆法、线性规划法、混合优化方法以及改进方法的理论分析，以伺服机构故障为例对各优化算法进行性能仿真对比分析，仿真中用到的评价因素主要包括计算效率、等效摆角误差、操纵能量消耗、等效摆角矢量夹角。

假设δdx=[δφ_SFδψ_SFδγ_SF]T中δψ_SF=5∘、δγ_SF=5∘，δφ_SF在0.1°～40°范围内变化，各伺服最大摆角限幅取5°，模拟SF21、SF41 机构失效。对以上算法进行仿真得到的结果如图5 所示。

图5 优化算法性能评估对比曲线Fig.5 Comparison curves for performance evaluation of optimization algorithms

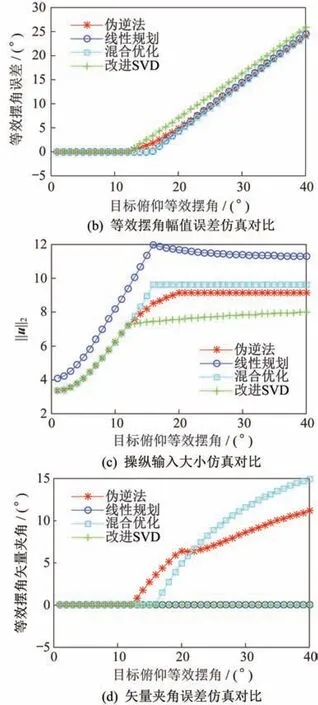
续图5 优化算法性能评估对比曲线ContinuedFig.5 Comparison curves for performance evaluation of optimization algorithms

首先，基于SVD 改进算法首先通过解除约束条件，SVD 得到满足分配方程所有解组成的可行解集，该解集可精确产生目标等效摆角；其次，通过缩放调整可行解集，使得新可行解集包含在约束边界形成的超平面内；然后，通过最小化可行解的无穷范数来最大化缩放因子得到满足共线特性的最优操纵输入，等价于线性规划解；最后，通过对最小化无穷范数的估计提高计算效率。

从图5（a）计算时间仿真对比可知，因改进方法使用范数估计，取消了迭代过程，显著提高了计算效率，使得改进方法和伪逆法具备最高的计算效率。而线性规划法需要迭代求解，导致计算时间增加。混合优化法计算时间与迭代步数直接相关，过高的迭代步数显著增加计算时间，而过低的迭代步数影响混合优化算法收敛效果。图5（b）等效摆角幅值仿真对比曲线表明，基于SVD 改进方法相比线性规划和伪逆法具有稍大的幅值误差。改进方法针对所有可行解集选取具备共线特性的最优解，在不使用范数估计时，理论上改进方法将获得与线性规划相同的解。范数估计在提高计算效率的同时，引入了估计误差。

图5（c）操纵输入对比可知改进方法具有较小的操纵输入。因线性规划法迭代过程容易使操纵输入陷入约束边界，易使伺服机构动作过大进入饱和状态。混合优化法通过加权值综合考虑了等效摆角误差和操纵能量消耗，使得操纵能量消耗相对较小。相比伪逆法，改进方法使用了缩放因子，因此，操纵输入相对较小。图5（d）矢量夹角仿真结果表明，改进方法和线性规划法由于具备输出共线特性，与目标等效摆角矢量不存在方向误差，而混合优化法和伪逆法方向误差随目标等效摆角增加而增大。

定义控制重构相对误差：

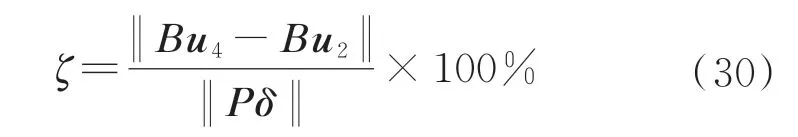
经推导，理论误差上边界为

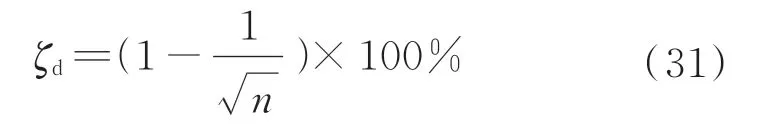
仿真算例实际误差、理论误差上边界绘制如图6 所示。由于实际操纵量集中在几个通道，因此范数估计引入的理论误差上边界与理论边界相差较远，实际误差近似上边界更接近算例中仿真实际误差。各伺服机构摆角控制曲线如图7、图8 所示。

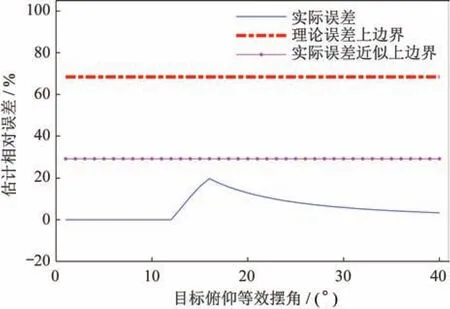
图6 范数估计引入的相对误差Fig.6 Relative error introduced by norm estimation

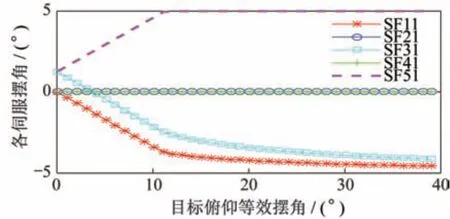
图7 俯仰方向伺服机构摆角控制曲线（SVD 改进方法）Fig.7 Swing angle curves of pitch servomechanism（improved method based on SVD）

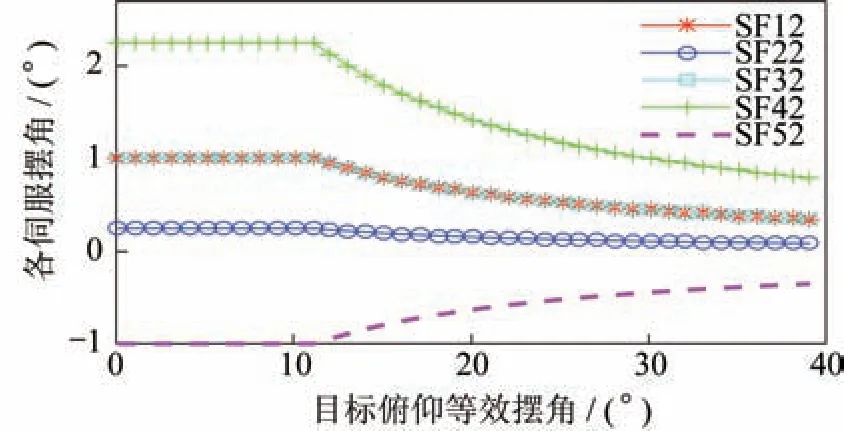
图8 偏航方向伺服机构摆角控制曲线（SVD 改进方法）Fig.8 Swing angle curve of yaw servomechanism（improved method based on SVD）

对比分析仿真性能，充分表明了改进方法具有操纵能量消耗相对较小的优势，同时结合了伪逆法计算高效、线性规划法输出共线的特点。改进方法的优势为：便于实现，控制不耦合，可实时计算，伺服机构能量消耗小等，而增加的相对较小的等效摆角误差可通过适当增加控制时长等方法弥补。

3.2 数学仿真验证

为考核基于SVD 的改进方法在运载火箭伺服机构故障重构控制中应用的可行性和有效性，需基于运载火箭带控制分配及合成闭环控制模型开展数字仿真验证。仿真算例条件为：起飞后30 s，助推器Ⅰ的SF21 卡死在5°，起飞后50 s，助推器Ⅲ的SF41 也卡死在-5°。仿真结果对比如图9～图14 所示。由图可知：SF21 在30 s 出现卡死故障后，如果不采取重构措施，在30～50 s，依靠箭体自身的鲁棒性，剩余正常伺服机构摆角增大，姿态角偏差振荡后收敛；但当SF41 在50 s 也发生故障后，伺服控制摆角限幅，姿态快速发散，而采用改进方法进行在线分配，可以实现伺服故障下控制力矩快速在线重构。同时，将故障伺服机构卡死摆角引入前馈控制，可实现姿态角偏差与正常状态一致，系统稳定，证明了该方法的可行性和有效性。

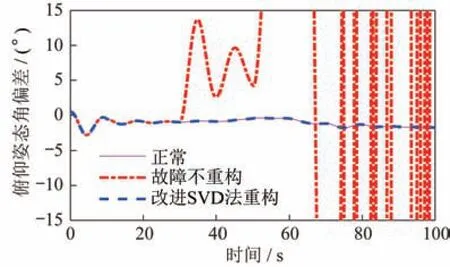
图9 俯仰姿态角偏差曲线对比Fig.9 Comparison of the deviation curves of the pitch attitude angle

图10 滚动姿态角偏差曲线对比Fig.10 Comparison of the deviation curves of the roll attitude angle

图11 伺服机构SF21 摆角曲线对比Fig.11 Comparison of the swing angle curves of servomechanism SF21

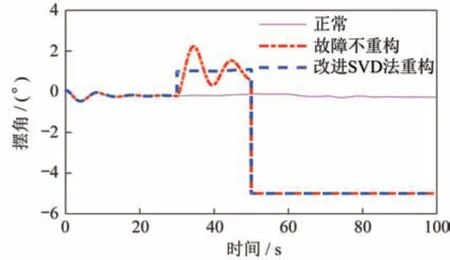
图12 助推伺服机构SF41 摆角曲线对比Fig.12 Comparison of the swing angle curves of booster servomechanism SF41

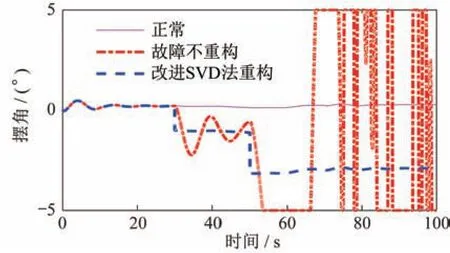
图13 芯级伺服机构SF11 摆角曲线对比Fig.13 Comparison of the swing angle curves of corestage servomechanism SF11

图14 助推伺服机构SF31 摆角曲线对比Fig.14 Comparison of the swing angle curves of booster servomechanism SF31

4 结束语

本文针对捆绑运载火箭飞行中伺服故障下控制重构问题，完成了对伪逆法、线性规划法、混合优化法3 种常用优化算法的分析和评估，并针对现有算法存在的缺点，提出了基于SVD 改进的控制重构方法。理论分析和性能仿真对比都充分表明该方法兼顾了伪逆法的计算高效、线性规划法的输出共线等优点，对不同构型火箭都有较高的拓展应用价值。通过开展运载火箭伺服机构故障重构控制的数值仿真，验证了该方法的可行性和有效性，证明可满足工程应用条件。