一类具有快速增权的非线性椭圆方程解的存在性①

郑文静， 陈尚杰， 李麟

1.重庆工商大学 数学与统计学院，重庆 400067；2.经济社会应用统计重庆市重点实验室，重庆 400067

考虑如下发展方程：

(1)

(2)

具体可参见文献[1].热方程作为抛物型偏微分方程，不仅可以用来描述热传导过程，也可以用来描述多种反应的扩散过程，诸如液体流动、传染病扩散、生物种群的迁移、生物分子的运动以及飞行器的冷却与保护等.目前关于用变分原理来研究相关增权问题解的存在性和不存在性，受到了国内外学者的广泛关注并取得了丰硕的研究成果.

文献[2]研究了在非线性项f(x，u)分别满足超线性条件和渐近线性条件的情况下，方程(2)基态解的存在性.除此之外，更多的学者研究了方程(2)中非线性项f(x，u)具有临界增长的情况，即如下方程：

(3)

其中

文献[3-8]研究了N≥3且非线性项临界增长的情况，通过改变方程(3)中a(x)，b(x)的取值及讨论q和参数λ的取值范围，分别得到了相应方程的基态解、非径向解、非径向对称基态解、变号解、衰减解、非平凡解和多解的存在性结论.文献[9-10]研究了方程(3)带有凹凸非线性项的情况，其中文献[9]运用极小化理论和山路定理证明了方程存在两个非负解，文献[10]在文献[9]的基础上，运用测试函数和山路定理得到了方程非平凡解的存在性.

与上述方程略有不同，文献[11]考虑了带非局部项的椭圆型偏微分方程

(4)

目前关于该类具有快速增权的方程的研究多限于非线性项为具体函数，如方程(3).而在非线性项为抽象函数(如方程(4)的右边)的情况下，该类方程的解是否存在，还尚未可知.

基于对以上带权重K(x)的方程的研究及文献[11，15]的启发，本文将研究如下一类带有一般非线性项的椭圆型方程解的存在性问题：

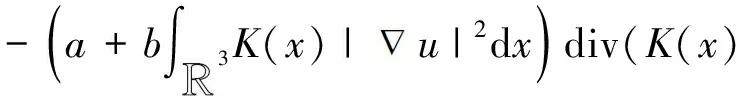
(5)

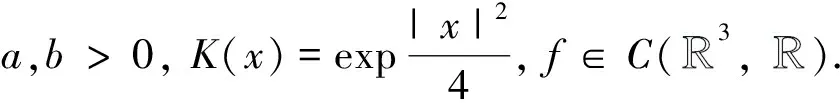
由于方程(5)不是点态恒等的，且其右端是一个抽象函数，我们不能确定范数项与非局部项的竞争关系.并且关于该类方程是否存在基态解这一问题，暂无学者做相关研究.因此本文不能利用文献[2，11]的方法证明方程(5)解的存在性.为了解决这一问题，受文献[2，15]的启发，本文考虑将方程放入一个加权的Sobolve空间中以解决空间失紧问题，并对非线性项f(x，u)做一些恰当的假设，利用山路定理来证明解的存在性.对非线性项f(x，u)的假设如下：

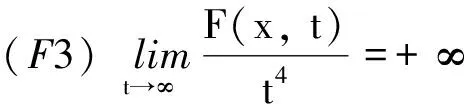
(F4)(局部AR条件) 存在l>0，C2>0，使得

本文的主要结果为：

定理1假设条件(F1)-(F4)成立，则方程(5)有一个非平凡解.

定理2假设条件(F1)-(F3)和(F5)成立，则方程(5)有一个基态解.

注1对于方程(5)，目前还没有类似的结论，且关于本文中给出的条件，可以找到满足条件的函数，如F(x，t)=t4log(1+|t|).

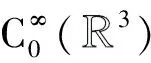
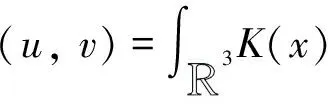
范数为

对∀q∈[2，6]，定义空间

对∀q∈[2，6]，可以定义

Sq=inf{‖u‖2：u∈X，‖u‖q=1}

方程(5)相应的能量泛函为

(6)

显然，I(u)是连续可导泛函，且其导数形式为

(7)

如果对∀v∈X，u∈X满足〈I′(u)，v〉=0，则u∈X是方程(5)的弱解.

Γ={γ∈C([0，1]，X)：γ(0)=x0，γ(1)=x1}

若泛函I满足(C)c条件(既对任何满足I(un)→c，(1+‖u‖)I′(un)→0的序列{un}都有一个收敛子列)，则c是I的一个临界值，且c>max{I(x0)，I(x1)}.

证设{un}是泛函I的一个(C)c序列，即满足

I(un)→c(1+‖u‖)I′(un)→0

(8)

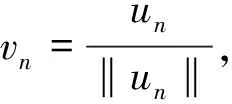
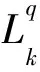
定义集合

则meas(B)≥0.下面分两种情况考虑：

情况1 若meas(B)>0，根据‖un‖→∞可以得到，当n→∞时，有|un|→∞(∀x∈B).因此，由Fatou引理可得

(9)

又由条件(F1)，(F2)和(F3)知，对∀M>0，存在CM>0，使得

(10)

因此由定理3有

(11)

根据(9)式和(11)式，当n→∞时，有

不等式两边矛盾，说明假设错误，则序列{un}是有界的.

-C3|t|≤f(x，t)≤C3|t|

因此存在C4>0，使得当|t|≤l时，

f(x，t)-4F(x，t)≥-C4|t|2

f(x，t)-4F(x，t)≥-C5|t|2

因此有

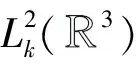
上面已证明对泛函I的任一(C)c序列{un}在空间X中都是有界的.现证序列{un}在空间X中有一个强收敛的子列.因为序列{un}是有界的，所以存在一个子列{un}(仍记为{un})和u∈X，使得

un⇀ux∈X

由(6)式和(7)式可以得到

整理得

当n→∞时，显然有

〈I′(un)-I′(u)，un-u〉→0

(12)

由序列{un}在X中的有界性，且在空间X中un⇀u，则当n→∞时，有

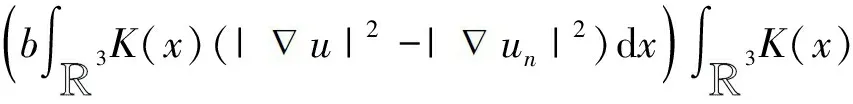
(13)

由条件(F1)，(F2)知，存在C6>0，使得

|f(x，t)|≤C6|t|+C6|t|p-1p∈[4，6)

结合Hölder不等式，有

(14)

结合(12)，(13)和(14)式可以得到‖un-u‖→0，证毕.

引理2设条件(F1)-(F3)成立，则泛函I满足山路几何结构：

(i)存在ρ，r>0，使得对任意的u(‖u‖=ρ)，有I(u)≥r；

(ii)存在φ∈X，使得‖φ‖>ρ和I(φ)<0.

证(i)由条件(F1)和(F2)知，对∀ε>0，存在Cε>0使得

结合定理3，有

又因ε任意小，而p∈[4，6)，因此存在ρ，r>0(ρ足够小)，对任意的u(‖u‖=ρ)，都有I(u)≥r>0成立.

令t足够大，则存在φ=tu使得‖φ‖>ρ和I(φ)<0.

定理1的证明从引理2可以看出，泛函I具有山路几何结构.而引理1已证明泛函I满足(C)c条件，从而泛函I有临界值，即存在u∈X满足I(u)=c>0，I′(u)=0，则u为方程(5)的一个非平凡解.

定理2的证明观察条件(F5)可以推出条件(F4)，因此将条件(F5)换成条件(F4)成立时，引理1和引理2均成立，因此由条件(F1)-(F3)和(F5)可以得出方程(5)有一个非平凡解.令

m=inf{I(u)：u∈X{0}，〈I′(u)，u〉=0}

假设u是泛函I的任意一个临界点，由条件(F5)得

因此

0≤m≤I(u)<+∞

设{un}是泛函I的临界点构成的序列，使得I(un)→m，因为u0是临界点，所以有I′(un)→0，因此{un}是在水平m上的一个(C)c序列，因而其存在收敛子列(仍记为{un})，设其极限为u0，易知I′(u0)=0，即u0为方程(5)的解.又由Fatou引理可得

因此，方程(5)存在一个基态解u0.