一类带有p-Laplacian算子的分数阶微分方程边值问题的多重正解①
胡芳芳, 刘元彬, 张永
1.伊犁师范大学 数学与统计学院,新疆 伊宁 835000;2.伊犁师范大学 应用数学研究所,新疆 伊宁 835000;3.新疆工程学院 数理学院,新疆 昌吉 830091
带p-Laplacian算子的微分方程主要来源于非牛顿流体理论和多孔介质气体的湍流理论.学者从多孔介质方程[1]中抽象出p-Laplacian方程,随后此类方程被广泛地应用到诸多领域,且p-Laplacian算子在许多物理工程的实际应用中可以更加具体地解释一些复杂的物理现象,所以,越来越多的学者研究带有p-Laplacian算子的分数阶微分方程解的存在性[2-6].
随着科学技术的进步和学者的深入研究,分数阶微分方程模型引起了数学学者们的广泛关注,在过去的几十年里,分数阶微分方程的成果丰硕[7-10],如:不同边值条件下的正解性,其主要研究方法包括锥上不动点定理、上下解方法、单调迭代方法等[11-13].
文献[14]利用Banach压缩映射原理和Guo-Krasnosel’skii不动点定理得到了以下具有p-Laplacian算子的边值问题
(1)
文献[15]利用Guo-Krasnosel’skii不动点定理和上下解方法得到了具有p-laplacian算子的Caputo分数阶微分方程边值问题
(2)
的正解存在性的一些新结果.其中
2<α≤3φp(s)=|s|p-2sp>1
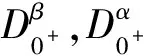
文献[16]运用单调迭代法得到了分数阶微分方程边值问题
(3)
的正解的存在性结果.其中
α<0γ≤2β>0 1+β≤α
0<ξ,η<1φp(s)=|s|p-2sp>1
Dα,Dβ是标准的Riemann-Liouville型分数阶导数.
基于上述研究,本文利用p-Laplacian算子考虑分数阶微分方程边值问题
(4)
1 预备知识

其中等式右端在[0,+∞)内有定义.

其中n是不小于α的最小整数.
引理1[18]设u(t)∈C[0,1]∩L1[0,1],且α>0,则
其中n是不小于α的最小整数.
引理2[18]设u(t)∈L1(0,1),且α>β>0,则
其中n是不小于α的最小整数.
引理3[18]设ρ>0,μ>0,则
引理4设y∈[0,1],1<β≤2,2<α≤3,则分数阶微分方程边值问题
(5)
有唯一解

(6)
其中
(7)
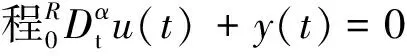
由边值条件
u(0)=u′(0)=0
可得
c2=c3=0
(8)
因为α>β,对(8)式两边进行β阶微分,可得
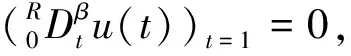
即
其中
引理5设g∈[0,1],1<β≤2,2<α≤3,则分数阶微分方程边值问题
(9)
有唯一解
(10)
其中
(11)
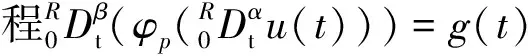
由边值条件
可得
d2=0
即
即
由引理4可知
引理6函数G(t,s),H(t,s)满足如下性质:
(i)对任意的t,s∈[0,1],G(t,s)≥0,H(t,s)≥0;
证(i)由函数G(t,s),H(t,s)的表达式可知(i)显然成立.
(ii)若0≤s≤t≤1,则一定有
0≤t-s≤t-ts=t(1-s)
因此
(t-s)α-1≤tα-1(1-s)α-1
当0≤s≤t≤1时,有
当0≤t≤s≤1时,有
即
(iii)若0≤s≤t≤1,则一定有
0≤t-s≤t-ts=t(1-s)
因此
(t-s)β-1≤tβ-1(1-s)β-1
当0≤s≤t≤1时,有
当0≤t≤s≤1时,有
即
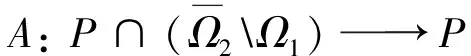
(i)‖Ax‖≤‖x‖(x∈P∩∂Ω1),‖Ax‖≥‖x‖(x∈P∩∂Ω2);
(ii)‖Ax‖≥‖x‖(x∈P∩∂Ω1),‖Ax‖≤‖x‖(x∈P∩∂Ω2).
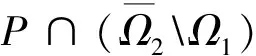
引理8[20]设P为实Banach空间E中的一个锥,
Pc={x∈P:‖x‖ P(θ,b,d)={x∈P:θ(x)≥b,‖x‖≤d} (i){x∈P(θ,b,d):θ(x)>b}≠∅,且对x∈P(θ,b,d)有θ(Ax)>b; (ii)当‖x‖≤a时,‖Ax‖≤a; (iii)当x∈P(θ,b,c)且‖Ax‖>d时,θ(Ax)>b. 那么A至少有3个不动点x1,x2,x3,满足 ‖x1‖ 记E=C[0,1],在E中定义范数 则E为Banach空间.定义锥P⊂E为 P={u∈E:u(t)≥0} 定义锥P上的非负连续泛函θ为 证设Ω是P的任意有界集,即存在一个常数γ>0,使得∀u∈Ω,都满足‖u‖≤γ.由于f(t,u(t))是连续的,则对于t∈[0,1],存在m>0,使得 0≤f(t,u(t))≤m 令 所有T(Ω)是一致有界的. 由于G(t,s)在[0,1]×[0,1]上是一致连续的,因此G(t,s)是一致连续的.对任意的ε>0,存在δ>0,使得当t1,t2∈[0,1],t1 于是 定理2假设f(t,u(t))为C[0,1]×[0,+∞)上的连续函数,其中 若存在两个正常数r2>r1>0,使得 (i)当(t,u(t))∈[0,1]×[0,r1]时,f(t,u(t))≥φp(Nr1); (ii)当(t,u(t))∈[0,1]×[0,r2]时,f(t,u(t))≤φp(Mr2). 则方程(4)至少有一个正解u,使得r1<‖u‖ 证令 Ω1={u∈P:‖u‖ 当u∈∂Ω1时,有 0≤u(t)≤r1t∈[0,1] 由(i)和引理6得 从而 ‖Tu‖≥‖u‖u∈∂Ω1 令 Ω2={u∈P:‖u‖ 当u∈∂Ω2时,有 0≤u(t)≤r2t∈[0,1] 可从(ii)和引理6得 从而‖Tu‖≤‖u‖,u∈∂Ω2. 总之,通过引理7可知,方程(4)至少有一个正解u,且满足r1<‖u‖ 定理3假设f(t,u(t))为C[0,1]×[0,+∞)上的连续函数,若存在满足0 (i)当(t,u(t))∈[0,1]×[0,a]时,f(t,u(t))≤φp(Ma); (ii)当(t,u(t))∈[0,1]×[b,c]时,f(t,u(t))≥φp(Nb); (iii)当(t,u(t))∈[0,1]×[0,c]时,f(t,u(t))≤φp(Mc). 则方程(4)至少有3个正解u1,u2,u3,且满足 下面证明引理8的条件(i)也是满足的.很明显, {u∈P(θ,b,d):θ(u)>b}≠∅ 若u∈P(θ,b,d),对任意的0≤t≤1有b≤u(t)≤d,通过(ii)可得 即对任意的u∈P(θ,b,d),θ(Tu)>b.因此满足引理8中的条件(i). 最后,我们证明引理8的条件(iii)也是满足的.对任意的u∈P(θ,b,c),都有θ(Tu)>b.因此,引理8的条件(iii)也成立. 综上所述,引理8的所有条件都满足.根据引理8,可以得出方程(4)存在3个正解u1,u2和u3,满足 例1考虑边值问题 其中 经过计算得 M≈1.766N≈2.949 应用定理3,例1至少有3个正解u1,u2,u3,且满足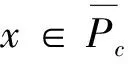
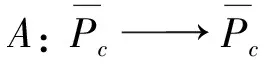
2 主要结论



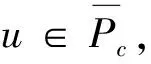
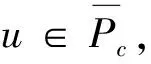
3 例子