重载长行程机械臂设计及力学性能分析

程 燚，吴斌方，石 康

(湖北工业大学机械工程学院，湖北 武汉 430068)

侯保林等[1]利用Houboult法求解重载高速送料机械臂的运动方程，针对做大刚体运动的典型机械系统获得具有普遍意义的运动规律。张莉[2]运用D-H参数法在静力学和模态分析基础上对重载冗余机械臂进行实操模拟和样机实验研究。武欣竹等[3]从伺服谐振和机械共振的角度对某桁架机械手的抖动现象进行分析，发现减速器输出轴连接键结构强度差是造成横梁振动的根本原因。毕厚煌等[4]设计出一种可实时调整碳棒电极高度的悬臂式起重机构，将丝杠机构柔性化以建立悬臂式起重机的刚柔耦合模型，对比刚体模型与刚柔耦合模型的仿真结果，获得更加接近实际运行情况的数据，为整体结构进一步优化打下基础。王相兵等[5]运用多柔体动力学理论，结合拉格朗日定理、虚功原理等，建立挖掘机机械臂柔性体模型，并对其进行仿真和数值求解，对比两种不同操作结果验证建模的正确性，同时，数值求解得到模态相关参数为结构的进一步优化提供参考。为了实现重载和长行程的生产需求，本文设计了一款全新的送料机械臂。

1 送料机械臂设计工作原理及应用

1.1 送料机械臂

由于棒料芯模较重，采用对称的双臂结构可有效增强机械臂承载能力。考虑到该棒料芯模两端均有低精度的圆柱面，芯模长5～13 m不等，采用对称联合作业的机械臂设计，不仅可以根据芯模实际长度调整距离，还能保证芯模在运输过程中的平稳性。此外，通过上部机械臂的左右运动将芯模在机床与机械臂间来回运输，机械臂底座上安装的轨道轮，可以实现在轨机械臂上的芯模长距离内外往复运输。机械臂整体行程不得低于2600 mm，上部机械臂行程设计为2380 mm，才能满足实际使用要求。送料机械臂主要由底座、伸缩系统及举升系统组成(图1)。

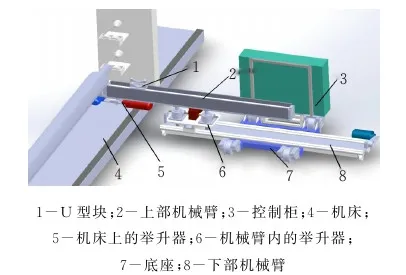
图1 送料机械系统结构

1.2 机械臂横梁构件

为了研究上部机械臂的固有频率和振型，将其从装配体中分离开来。上部机械臂主要包括两端的丝杆支撑座、连接举升机构的连接板、连接板两侧的加强筋和在导轨上滑动的滑块等几个部分组成(图2)。该结构主要为钢材焊接，在焊接后进行热处理以消除应力，在对其进行力学模型仿真分析时，可忽略焊接应力的影响，建模过程将其视为一个整体进行分析。

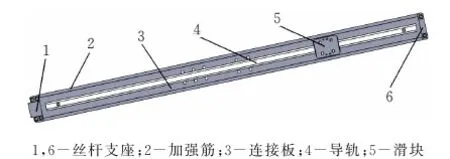
图2 上部机械臂组成结构

送料机械臂主要结构参数如表1所示。

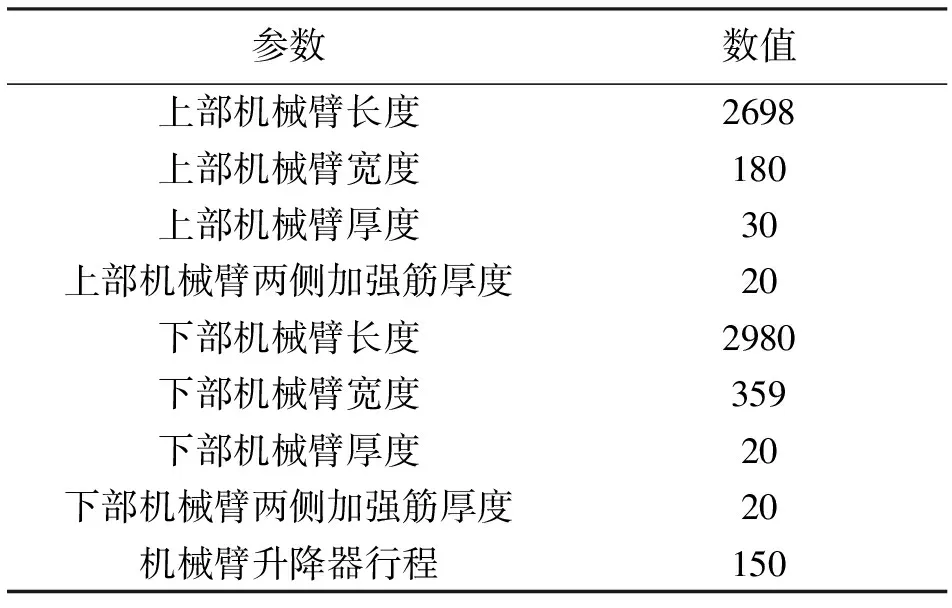
表1 机械臂的主要结构参数 mm

1.3 重载长行程机械臂

考虑到两机床中心距长达4938 mm，运行轨道距两侧机床中心距分别为2410 mm和2528 mm，而生产中心的门宽仅为3 m，故该机械臂设计为上下伸缩式结构，以保证送料机械臂满足同时运输两侧芯模的要求。芯模为阶梯轴类棒料芯模，芯模两端为可运输端，精度低；中间部位为缠绕成型区，精度极高。故考虑用U形块来承接该棒料芯模，利用对称机械臂进行联合作业，将棒料芯模运送到指定地点。图3、4为2～12 t棒料芯模的实物以及机床原始位置摆放。

图3 棒料芯模实物

图4 机床原始位置摆放

2 上部机械臂有限元分析

2.1 有限元模型的建立

在有限元分析之前，在不影响求解精度的条件下，对模型进行适当简化处理，忽略主体结构中的凹槽、倒角、小孔等加工细节，避免产生应力集中的现象。在不影响机械臂横梁强度的前提下，通过SolidWorks建立模型，并导入至ANSYS Workbench中，以满足有限元分析的要求。得到简化后的模型如图5所示。

图5 上部机械臂有限元分析模型

2.2 有限元模型网格划分

上部机械臂总体呈现细长梁形状，总长2698 mm，宽180 mm，高240 mm。由于上部机械臂主要用于承重，故最终选用的材料为结构钢Q235以保证机械臂的抗弯和承载能力。上部机械臂主要使用板材焊接。为保证其网格划分的质量，采用手动精细的网格划分方法以增加求解结果精度。划分成后，网格节点共计123311个，网格单元45614个。划分完成后的模型如图6所示。

1.2 仪器与设备 GC-MS-2010-plus型气相色谱-质谱联用仪，配有EI源，四级杆质量分析器；GC-MS Solution，日本岛津公司；NIST05版质谱图库；DHG-9070A型电热恒温鼓风干燥箱，上海一恒科学仪器有限公司；57330U型手动SPME萃取手柄及65 μm聚二甲基硅氧烷-二乙烯基苯(PDMS/DVB)萃取探头；20 mL精密螺纹口透明玻璃顶空进样瓶，美国Supelco公司。

图6 A级机械臂网格划分

2.3 约束条件及边界条件设置

定义上部机械臂中连接板方向为X方向，右端为正，沿着重力方向为Y方向，方向竖直向上，Z方向为丝杆支座方向，朝着操作者的方向为正。

对机械臂横梁臂添加约束。由于上部机械臂与举升机构相连接，故在上部机械臂上将位于下底面中心的10个孔位进行固定端约束。同时，当上部机械臂向左侧伸出，运载型芯时，机械臂左侧会搁置在机床上，防止型芯过重而导致机械臂发生侧翻。故在机械臂左侧设置固定端约束(图7)。

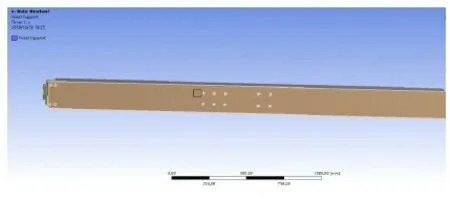
图7 上部机械臂约束

由于该机械臂的主要外力来源于型芯的压力以及自重，且型芯自重为12 t，为保证机械臂的正常使用，分析时将其设计为16 t；考虑到该机械臂采用一对对称的机械臂进行联合作业，对称的机械臂同时运载型芯时，每个机械臂均受到8 t外加载荷以及自身重力。根据上部机械臂的结构，当滑块位于上部机械臂右侧中点时，为上部机械臂的危险状态。对横梁添加的外力和重力如图8所示。

图8 横梁有限元分析载荷设置

2.4 有限元分析

对上部机械臂机械应力应变分析。上部机械臂在静力作用下的最大应力应变如图9所示，其中最大应变为0.090493 mm，最大应力为90.08 MPa，远小于材料的许用应力应变值。故结构强度符合机械臂的使用要求，不会出现在应力作用下被破坏的情况。

图9 机械臂在静力作用下的应力应变

对上部机械臂进行应力应变分析后，还需对其进行模态分析。图10为上部机械臂前六阶的振型云图，可知其固有频率在67.4671～312.61 Hz之间。

图10 上部机械臂的的前六阶振型云图

可以看出第一阶振形沿Z轴方向向内弯曲，第二阶振形沿Y轴方向向上弯曲，一、二阶振形最大变形量均发生在机械臂横梁左侧；第三阶振形是沿Z轴方向弯曲扭转，最大变形发生在机械臂横梁左侧；第四阶振形是绕Y轴扭转，横梁右侧变形较大；第五阶振形为Y、Z轴方向的扭转，最大变形量发生在机械臂横梁左侧；第六阶振形是沿Z轴扭转，最大变形出现在横梁中心附近。

3 上部机械臂的谐响应分析

在工作过程中由于轨道不平稳，上部机械臂受到来自外加载荷产生的周期性作用力，当作用力的频率与机械臂的固有频率相同时，将发生共振。

谐响应分析的通用方程

(1)

力矩阵F和位移矩阵{u}是简谐的，频率为ω，用复数形式表示为：

{F(t)}={Fmaxeiφ}eiωt=({F1}+i{F2})eiωt

(2)

{u(t)}={umaxeiφ}eiωt=({u1}+i{u2})eiϖt

(3)

φ为位移函数的相位角；实部u1=umaxcosφ；虚部为u2=umaxsinφ。

谐响应分析的运动方程为：

(-ω2)[m]+iω[C]+

[K]({u1}+i{u2})=({F1}+{F2})

(4)

谐响应运动的求解方法主要有：完全法和模态叠加法，其中最快速的求解方法是模态叠加法。模态叠加法计算原理是将模态分析中的特征向量乘以因子，然后求和即可。

对上部机械臂进行谐响应分析时，在滑块上施加一个激振力F，大小为68 600 N，在Workbench的Harmonic Response模块中观察上部机械臂在0～500 Hz频率范围内不同频域下最大变形趋势(图11)。

图11 上部机械臂0～500 Hz谐响应

由图11可知，在0～500 Hz的激振频域范围内，上部机械臂频率在100 Hz处时，最大变形为0.1194 3mm，此时上部机械臂发生共振现象。

4 上部机械臂的模态试验

通过模态分析结果可知，共振对上部机械臂及其两侧加强板影响最大，这将直接影响机械臂运输过程中的平稳性，甚至对机械臂整个系统造成破坏。因此，通过谐响应分析判定机械臂的持续动力特性，确保整个机械臂能够承受各种不同频率的正弦载荷。

为验证有限元模态分析结论的可靠性，对横梁进行力锤单点敲击，通过获取其他点多点响应的测试方法进行了模态试验(EXP)。试验过程中，将软绳连接悬梁并连接至模态分析传感器，通过传感器得到横梁主要部位的振动位移信号。将采集到的激励信号进行记录后，通过分析软件识别系统的模态参数。试验所得结果(FEM)与有限元计算结果对比(FEW)如表2所示。

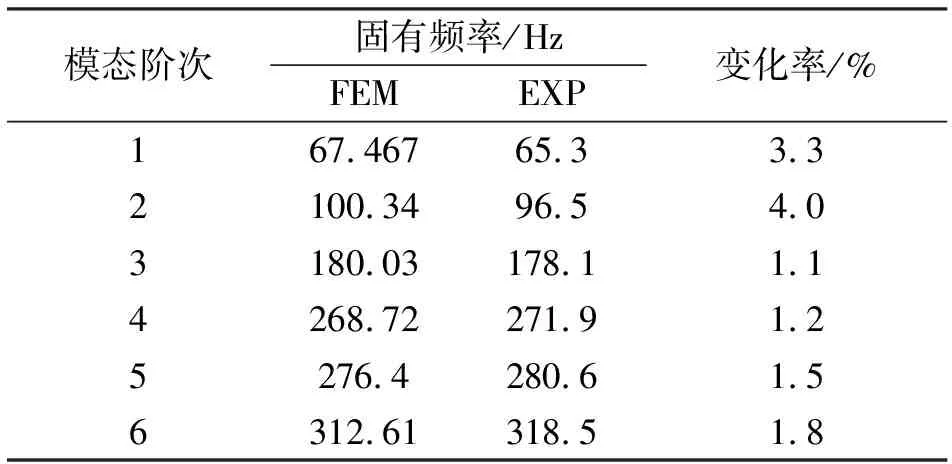
表2 横梁模态试验与有限元计算结果对比

由表2可知，模态试验与模态分析计算结果相比较，最大误差4.0%发生在第二阶模态分析处。该试验结果与有限元分析结果较为吻合，充分证明了采用有限元分析方法对自动上料机械臂进行模态分析时具有快速、可靠的优点。通过刺激频率和计算频率进行比较，避开固有频率，可以有效防止系统共振带来的影响，在一定程度上证明了本次试验方法对于机械臂设计的参考价值。

5 结论

1)根据生产需求，设计了一款重载长行程送料机械臂，并且通过有限元软件进行静态分析，得出最大应变为0.090 493 mm，最大应力为90.08 MPa，远小于材料的许用应力应变值，结构强度满足2～12 t棒料2700 mm长行程输送的设计要求。

2)通过六阶模态分析云图可以看出，上部机械臂的最大位移约为6 mm，位移距离较大，故需对各板材进行不同程度加厚，或者在合适的部位添加加强筋来保证机械臂的刚度。通过谐响应分析可以看出，当上部机械臂频率在100 Hz时，最大变形为0.119 43 mm。

3)对该送料机械臂进行模态实验研究，对比有限元分析结果，得出最大误差为4.0%，发生在第二阶模态分析处。该试验结果与有限元分析结果较为吻合，为避免共振提供了数据支持，为解决类似问题提供很好的借鉴。