共轴多组充退磁线圈均匀磁场优化设计研究
张健 陈绍露 张绍华 郭涛 刘超波 肖琦
(1 北京宇航系统工程研究所,北京 100076;2 北京卫星环境工程研究所,北京 100094)
0 引言
磁场模拟装置在航天器磁性控制[1-4]、舰船消磁等领域有着重要的应用[5,6]。磁场线圈是磁场模拟装置的主要组成部分,中心区域的磁场均匀度是关键技术指标之一[7-9],对其性能有直接影响。方形赫姆霍兹线圈是最简单的磁场线圈形式,加工制作方便,并且可以通过增加几何尺寸来满足均匀区指标要求,但是其代价是线圈常数降低,电源功耗增加,尤其在线圈空间尺寸受到限制时,均匀性指标很难满足设计要求。所以,在磁场均匀性要求较高,工程安装空间有限,励磁电源功耗受限等情况下,可以采用共轴多组线圈组合的方式加以解决。
随着线圈组数增多,各组线圈尺寸、安装位置、线圈匝数、电缆截面、电感电阻等参数,存在众多的组合形式,如果选择不合理会使得磁场均匀性降低,工程代价增加,甚至不能满足设计要求。所以,需要结合工程可行性约束条件进行优化设计与计算分析,使其综合指标性能达到最优。
线圈参数的计算有多种方法,常用的有高阶求导法[10,11]、智能优化法[12-16]等。随着线圈组数的增加,待优化参数也相应增加。张伟等利用磁位的拉普拉斯方程在球坐标系下的解,给出了典型的多段环形线圈的设计方法和过程[7];对于高阶求导法,4对线圈参数优化需要8阶求导[10],9对参数优化需要16阶求导[11],高阶求导法十分复杂。吕志峰等针对多线圈均匀磁场优化设计中的高阶求导及优化结果可信度评估问题,提出一种基于粒子群优化算法和有限元法相结合的多线圈均匀磁场优化设计方法[12];王志峰等利用差分进化算法对线圈的均匀磁场进行优化设计[13]。
多组线圈参数的计算问题可以归结为求解由物理指标(如磁场均匀度指标等)和工程约束条件(如线圈安装空间等)耦合的目标函数。线圈优化的目标函数中包含非线性函数,是非线性规划问题。非线性规划目前还没有适用于各种问题的一般算法,已有的各种方法都有其特定的适用范围。序列二次规划(Sequence quadratic programming,SQP)算法是目前公认的求解约束非线性优化问题最有效的方法之一[17-19]。与其他算法相比,序列二次规划法的优点是收敛性好、计算效率高、边界搜索能力强,因此受到了广泛的重视及应用。本文使用序列二次规划方法进行共轴多组充退磁线圈系统优化设计,通过优化线圈位置和驱动电流等参数来实现所需的磁场均匀度指标,并且给出了典型的多组矩形线圈在不同工程边界约束条件下的线圈优化参数、磁场均匀区及电参数的计算结果。
1 线圈参数及磁场计算
方形线圈和圆形线圈是工程中常用的两种线圈形式。方形线圈具有结构简单,加工制作方便的优点。不失一般性,本文以共轴正方形多组线圈为例,对磁场分布的均匀性指标进行参数优化研究。
图1 给出4个方形赫姆霍兹线圈系统及线圈离散单位电流元产生磁场示意图,坐标原点位于充退磁线圈系统的中心点。4个线圈大小相同,边长均为a。在实际应用中为保证励磁电流的同步性,4个线圈串联,通过电流为I,并假定逆着x轴正方向看电流是逆时针方向。需要说明的是,虽然每个矩形线圈的尺寸可以不同,但是考虑实际加工制作及工程应用,通常设置为相同的大小尺寸。为了满足轴向整体磁场的对称性,线圈绕制匝数也成对相等。因此,内侧线圈距离d1,线圈匝数相同,均为N1匝;外侧线圈距离d2,线圈匝数相同,均为N2匝。预先固定线圈边长a,需要优化的线圈参数有三组,即d1,d2和内外线圈电流比例(即,ck12=N1/N2)。随着线圈匝数增多,相应的待优化参数增加。
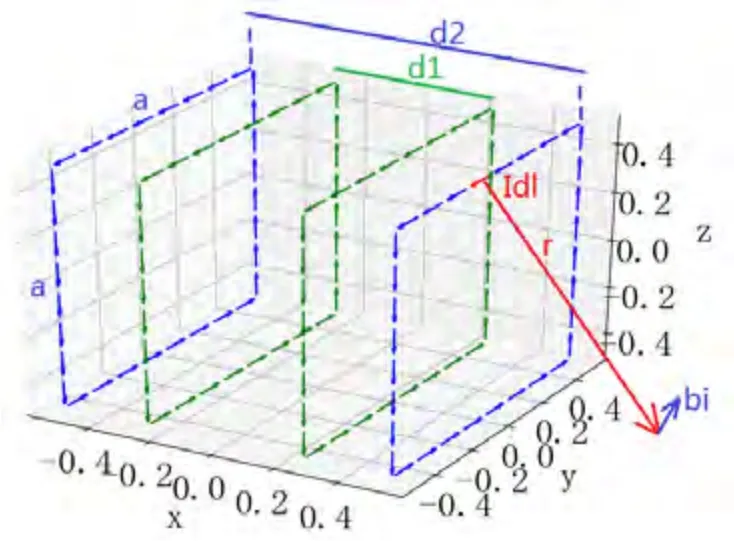
图1 4个方形赫姆霍兹线圈系统及线圈离散单位电流元产生磁场示意图Fig.1 Schematic diagram of 4 square Helmholtz coil systems and coil discrete unit current elements to generate magnetic field
优化时需要计算线圈系统在优化区域内多个空间点的磁场。对于方形线圈的磁场计算有很多种方法。解析法在中轴线上的磁场计算相对简单,但是偏离中轴线的磁场矢量解析公式非常复杂。有限元方法在计算大尺寸空心线圈的三维空间磁场时,对于细导线的网格划分与空间点的网格划分差别巨大,导致离散网格点过多、计算耗时甚至解不收敛。本文采用离散积分的方法来计算消磁线圈在空间点的磁场分布。把线圈电流等效为理想线电流模型,线圈离散成微小的电流矢量单元,根据毕奥萨伐尔公式,每个电流矢量单元在某个空间点P的磁场矢量计算公式如下:
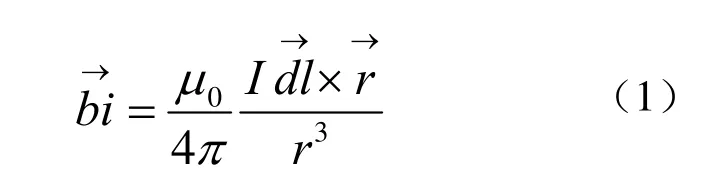
2 优化过程
共轴多组充退磁线圈均匀磁场优化设计过程如下:1)确定线圈组数及待优化参数;2)给出磁场均匀度的目标函数,并结合工程实际给出物理参数边界条件;3)采用序列二次规划优化算法对目标函数进行迭代寻优;4)线圈匝数取整化,再次寻优计算;5)数值仿真验证指标。
2.1 确定线圈组数及待优化参数
优化设计首先需要确定充退磁线圈所采用的线圈组数及对应的待优化参数,通常待优化参数随着线圈匝数增多而增多。例如:4线圈系统待优化参数有3个,即内线圈距离d1、外线圈距离d2及内外线圈电流比例ck12;6线圈系统的优化参数增加为5个,即内中外三对线圈的距离d1、d2、d3,中线圈与最内线圈电流比ck12,最外线圈与最内线圈电流比ck13。
2.2 定义磁场均匀度指标目标函数
一般采用磁场偏差来衡量磁场均匀度指标大小,磁场偏差值越小,表明磁场均匀度越好。在考察空间内取m个计算点,以线圈系统中心的磁场强度B0为参考,第i个考察空间点的磁场偏差定义为:

本文采用磁场平均相对误差作为磁场均匀度指标的目标函数,平均相对磁场偏差定义为:
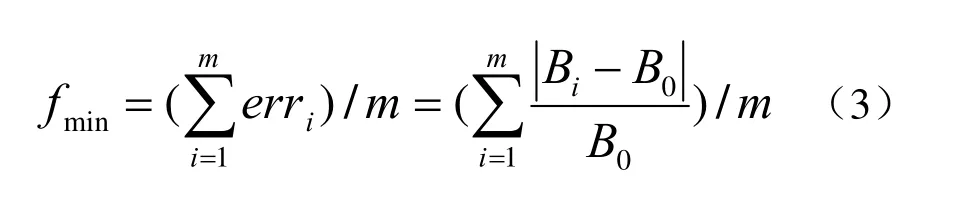
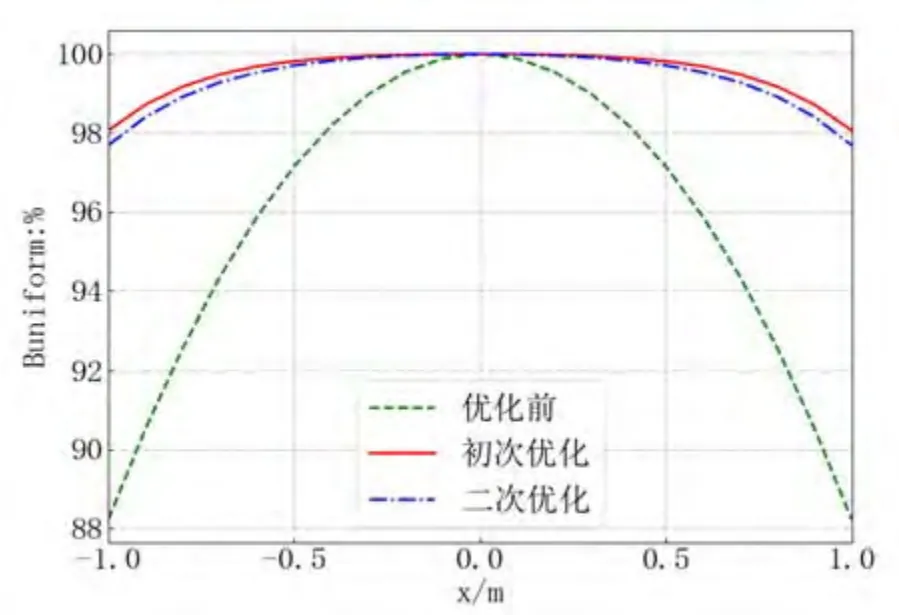
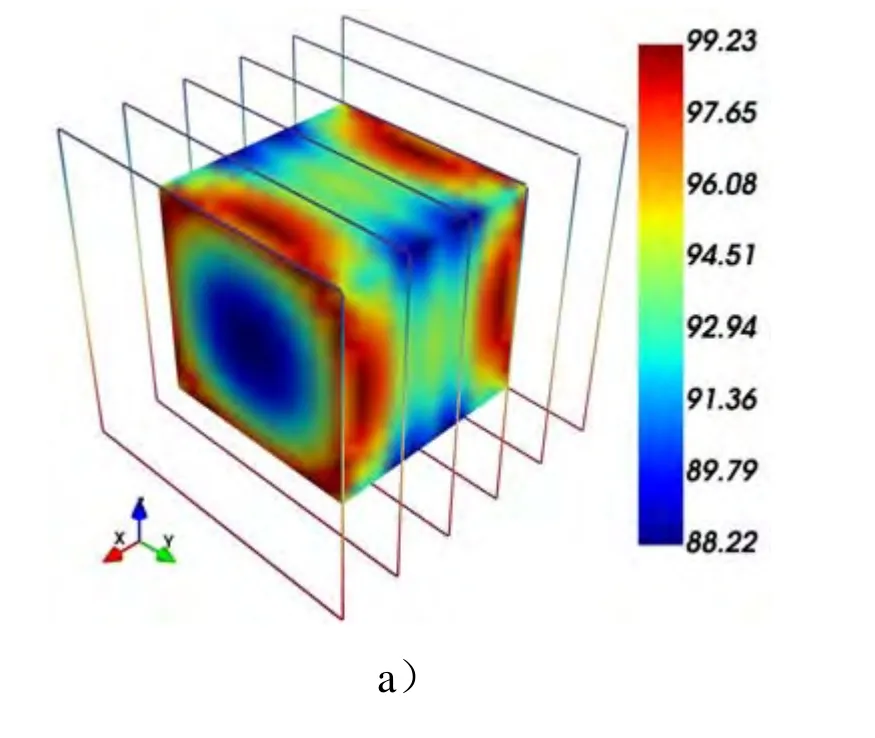
式(3)中,m为网格点总数。根据式(3),可以引入平均相对磁场均匀度指标越大代表磁场均匀度越高。根据2.1知道,对于4线圈系统是关于参数(d1,d2,ck12)的函数,对于6线圈系统是关于参数(d1,d2,d3,ck12,ck13)的函数。实际工程对线圈距离有限制,体现为待优化参数的边界条件,一般要求d2>d1,d3>d2,d3 线圈优化的目标函数 minf是非线性函数,并且通常包含多个约束条件,本文采用的序列二次规划算法是公认的求解约束非线性优化问题最有效的方法之一。序列二次规划把问题的求解主要分为两个步骤:第一步为通过泰勒展开,将原非线性优化问题转换为简单的二次优化问题;第二步为对简单的二次优化(QP)问题进行迭代搜索求解。在序列二次规划(SQP)的迭代过程中,每一步都需要求解一个或多个二次规划(QP)子问题。序列二次规划(SQP)算法流程见图2,具体算法参考文献[16-18]。 图2 序列二次规划(SQP)优化算法流程图Fig.2 Sequential Quadratic Programming (SQP) Optimization Algorithm Flowchart 线圈匝数需要整数化处理。步骤2.3对于磁场均匀度目标函数 minf计算中以内线圈电流I0=1A为基准,利用2.3中优化参数计算出线圈系统中心磁场强度B0。如果指标要求的中心点最大磁场强度为Bmax,励磁电源系统允许的最大电流为Imax,那么Bmax/B0就是线圈系统的安匝数,N1=Bmax/(B0*Imax)就是系统最内线圈组单个线圈的匝数,N2=N1/ck12=Bmax/(B0*Imax*ck12)是第2个线圈组单个线圈的匝数,N3=N1/ck13=Bmax/(B0*Imax*ck13)是3个线圈组单个线圈的匝数。这里用迭代寻优线圈电流比例系数计算得到的线圈匝数(N1、N2、N3)通常不是整数,而实际加工绕制都是以整数绕制的,所以需要对线圈匝数进行整数化处理。为保证线圈中心最大磁场强度,一般需要对小数向上取整。线圈匝数整数化之后,其它线圈参数就不是最优了,因此需要固定线圈匝数整数化后的电流比例,对其它的可变参数以步骤2.3的结果为初始值,并在较小区域范围内进行二次寻优计算,得到最终线圈系统最优参数。 通过以上过程计算得到线圈系统的最优参数后,需要进行数值仿真计算,检验在该参数条件下磁场的均匀性指标是否满足技术指标要求。此外,需要综合考虑其它工程约束条件是否满足,如线圈系统电阻、电源最大功耗、电缆总重量等。如果不满足,则需要调整线圈系统的约束条件,如线圈个数或者线圈组合形式等,重新进行优化计算。在线圈加工过程中受到加工精度、加工公差及线圈绕制精度的影响,实际的磁场均匀度指标可能会与理论仿真计算结果有一定偏差,所以对于目标函数的优化计算一般需要留有一定余量,例如,如果某区域的目标函数是平均相对磁场均匀度 %100)1(min×-f不低于90%,也就是平均相对磁场偏差 minf<10%,在理论计算中可设置稍微严苛一些,如要求目标函数 minf必须不大于8%,为工程加工留有2%的余量。 结合工程应用,给出一个共轴6线圈充退磁系统的设计实例。为了给某系列包络尺寸不大于2m的卫星充退磁,要求设计一个空间尺寸长宽高不大于3m的方形共轴赫姆霍兹充退磁线圈系统,最大线圈间距3m,中心待考察卫星工作区域2m×2m×2m立方体均匀区的磁场均匀度不低于95%,中心点最大磁场强度不低于5mT,电源峰值电流不大于100A,充退磁励磁电源最大功耗不大于40kW。 下面给出该设计实例的优化计算过程及结果。根据普遍采用的方式,优化前的线圈宽度a=3m,6个线圈等间距(线圈间距3/5m),电流相等。设计优化计算中采用平均相对磁场偏差函数作为优化目标函数,以待考察中心区域的总体磁场偏差作为优化目标,而不是只考虑某一个点的磁场偏差。 表1给出了优化前、初次优化及线圈匝数取整二次优化的参数结果。优化前采用最常用的线圈参数,即6线圈等间距分布,匝数相等,d1=3/5m,d2=9/5m,d3=3m,ck12=1,ck13=1,中心待考察的2m×2m×2m立方体区域内的平均相对磁场偏差值为0.073428,最低均匀度为88.22%。初次优化后得到的最优线圈参数,d1=0.4426m,d2=1.3610m,d3=3m,ck12=0.8827,ck13=0.2630,中心待考察的2m×2m×2m立方体区域内的平均相对磁场偏差值为0.003259,最低均匀度为95.95%。优化前与初次优化对比,看出预定区域内的平均相对磁场偏差降低到了优化前的1/23,表明区域内的整体磁场均匀度都得到了很大提高。同时,预定区域内的最低磁场均匀度也由88.22%提高到95.95%。 表1 参数计算结果对比Table 1 Comparison of parameter calculation results 要求的中心磁场强度为5mT(即5000000nT),优化前单位电流(1A)得到的线圈常数为1536.58nT,最大允许电流为100A,则单个线圈匝数5000000/1536.58/100=32.53,取整为33匝,6个线圈共198匝;初次优化,以最内线圈通电1A为基准,计算得到的线圈常数是2579.58,所以计算得到充退磁线圈系统最内、中间、最外三组线圈的匝数分别为N1=5000000/2579.58/100=19.38,N2=N1/ck12=19.38/0.8827=21.95,N3=N1/ ck13= 19.38/0.2630=73.69。对称线圈匝数向上取整数之后,N1=20匝,N2=22匝,N3=74匝,线圈系统的总匝数为2×(N1+N2+N3)=232匝。 线圈匝数整数化之后,对于线圈距离参数进行二次寻优,得到d1=0.4272m,d2=1.3753m,d3=3m,ck12=20/22=0.86956,ck13=20/74=0.27027,中心待考察的2m×2m×2m立方体区域内的平均相对磁场偏差值为0.004858,最低均匀度为96.26%。线圈匝数取整并二次优化之后与初次优化相比较,最内与中间线圈组的间距d1与d2有稍微调整,平均相对磁场偏差值从0.003259增加到0.004858,符合预期。 图3是沿着线圈中心轴x=[-1m,1m]范围内,优化前、初次优化及线圈匝数取整二次优化的磁场均匀度对比图,虚线是优化前线圈等间距、等电流(匝数)的计算结果,实线是初次优化之后的结果,虚点线是匝数整数化之后二次优化的结果。由图2可知,优化前线圈系统在中心轴的磁场均匀度分布极其不均匀,不能满足技术指标要求,只有在x=[-0.6m,0.6m]范围内大于95%。初次优化后,在线圈中心轴x=[-1m,1m]区域范围内磁场均匀度整体提高到97.5%以上。在线圈匝数取整二次优化之后,均匀度稍微降低,但整体均匀度变化不大,仍然在97.5%以上。 图4中的子图(a)(b)(c)分别是优化前、初次优化及线圈匝数取整二次优化在中心区2m×2m×2m立方体表面的磁场均匀度分布图。图中的方框是6个方形线圈的位置,给出了中心区立方体6个表面的磁场均匀度等值面分布图。由图3(a)看出,待考察的立方体区域表面最低磁场均匀度88.22%,并且大部分表面磁场均匀度值低于90%,不满足磁场均匀度95%的指标要求。从图4(b)、(c)看出,全部区域满足磁场均匀度大于95%的指标要求;磁场均匀度在立方体的8个角点附近相对略差,其值大约在96%附近,这也符合矩形线圈在角点附近的磁场均匀度偏差的普遍规律。在4个侧面的大部分区域磁场均匀度在98.9%以上。所以,线圈系统优化之后整体磁场均匀度分布有显著提高,更能满足充退磁线圈对于中心工作区域的均匀度指标要求。 图3 沿着线圈中心轴x=[-1m,1m]范围内,优化前、初次优化及线圈匝数取整二次优化的磁场均匀度对比Fig.3 Along the coil central axis x=[-1m, 1m], the comparison of the magnetic field uniformity before optimization, the first optimization and the second optimization of the rounded number of coil turns 图4 均匀区磁场均匀度分布图,a)b)c)分别是优化前、初次优化及线圈匝数取整二次优化的结果Fig.4: The distribution diagram of the uniformity of the magnetic field in the uniform area, a) b) c) are the results of the optimization before optimization, the first optimization and the second optimization of coil turns 线圈尺寸优化设计完成后,需要根据充退磁电源允许的峰值电流和最大功耗等参数,选取电缆的尺寸,估算线圈电缆总电阻、总重量、电源功耗等。本设计方案允许的最大电流为100A,根据经验选取直径4mm的漆包铜线作为绕线电缆。铜线电阻率ρ通常取值1.75×10-8Ω/m,铜线电阻计算公式如下: 式(4)中a为方形线圈宽度,Nc为线圈系统总匝数,d为铜线直径取值4×10-3m。 分别对优化前及匝数取整二次优化的线圈物理常量进行计算,表2给出线圈物理常量的计算结果对比。得到优化前(Nc=198匝)的充退磁线圈参数:长度2376.00m,电阻3.31Ω,功耗33.09kW,重量265.73kg;线圈匝数取整二次优化(Nc=232匝)的充退磁线圈参数:长度2784.00m,电阻3.87Ω,功耗38.77kW,重量311.36kg。虽然优化设计后的线圈系统匝数、功耗与重量增加约17.2%,但是在中心待考察卫星工作区(2m×2m×2m立方体区域)的平均相对磁场偏差降低到了优化前的1/23,整体磁场均匀度得到了极大提升。 表2 线圈物理常量计算结果对比Table2 Comparison of calculation results of coil physical constants 本文基于序列二次规划(SQP)方法,对共轴多组充退磁线圈进行系统优化设计。用离散积分的方法计算消磁线圈在空间点的磁场,以待考察区域的平均相对磁场偏差作为优化目标函数,并考虑工程约束条件,优化计算出不同线圈位置和驱动电流等参数。对线圈匝数整数化后进行二次优化,提高了均匀区的指标。结合一个实际工程中的共轴6线圈系统设计案例,给出了详细的优化步骤及结果,对于线圈匝数取整及二次寻优有详细阐述。仿真计算结果表明,经过优化设计后的共轴充退磁线圈系统的磁场均匀度得到了极大提升,在中心待考察卫星工作区的平均相对磁场偏差降低到了优化前的1/23,其它电参数均能满足技术指标要求。2.3 序列二次规划算法迭代寻优

2.4 线圈匝数整数化及二次寻优
2.5 线圈系统均匀性指标验证
3 线圈设计实例

3.1 线圈匝数整数化处理

3.2 线圈电参数计算
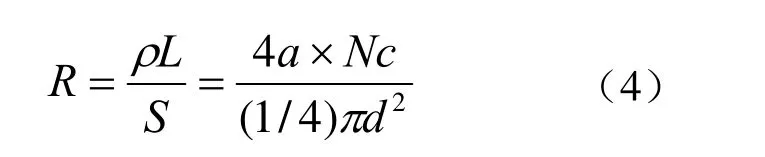

4 结论

