一种基于Logistic方程的图像加密算法

张应征,吴杰,涂立

(1.湖南工程职业技术学院 信息工程学院,湖南 长沙,410151;2.华中科技大学 计算机科学与技术学院,湖北 武汉,430074)

随着计算机技术与互联网应用的飞速发展,信息加密技术显得越来越重要,但传统的加密方法在图像加密方面存在局限性,如加密效率低、对大数据和像素间相关性很高的图像加密不适用等,而混沌作为一种复杂的非线性系统,对参数和初值的敏感度高,具有良好的遍历性和伪随机性,特别适用于加密,因此,近年来混沌理论被越来越多地应用到密码学。

本文拟首先分析混沌系统的特点,在一维Logistic混沌方程的基础上提出广义Logistic方程的模型,在分析研究广义Logistic方程的相图轨迹基础上,设计一种带有一次耦合项的二维广义Logistic方程,然后利用该方程生成一些具有随机性的序列,再将这些序列优化,并进行分段映射与仿真。

1 Logistic方程

Logistic方程是一个简单的非线性方程,又叫虫口模型[1],表示法为

其中0≤xn≤ 1,n∈ Z,0≤u≤ 4,u称为分岔参数,采用不同的u值进行迭代计算,整个系统会呈现出不同的特性。Logistic方程产生的序列由x的初值x0和分岔参数u控制,其中只要任何一个值有细微的差别,经过多次迭代计算以后,都会得到完全不同的实数序列[2],经过迭代计算后的效果图如图1所示,其中纵坐标表示输出序列分布x的范围;横坐标表示分岔参数u的取值范围(参数u取[0,4]的值)。

由图1可知:(1)当0≤u≤ 1时,无论选用什么样的初值x0,经过多次迭代计算后,最终产生的数值将是1个稳定值0,在这个范围内,系统没有混沌特性;(2)当1≤u≤ 3时,产生的迭代值是一个稳定的非0值;当u大于3时,系统将出现2个分岔,u=3是一个临界点;(3)在处,系统演化成4周期,也就是说,无论取什么初值xn系统都会稳定地收敛到一个4周期函数;当后,大量的倍周期分支出现在更加窄狭的u区间间隔里,这种周期倍化的演化过程没有限制,但相应的u有一个极限值:u=3.569 945 67…,当3.569 945 67＜u≤ 4时系统进入混沌区间。由图1可知,当3.569 945 67＜u≤4,初值x0经过迭代计算产生的序列是非周期性的,系统没有收敛性。

美国数学家Feigenbaum得出了一个结论:一个系统一旦发生倍周期分岔,必然导致混沌[3],并从Logistic方程发现该系统由倍周期分岔通向混沌的2个普适性常数,后来被称为Feigenbaum常数[4]。Logistic方程通过迭代计算可以产生一序列随机数列,这些随机数列可以应用于各种加密算法。加密是为了安全采取的一种手段,尽管Logistic方程有一定的优点,但是也存在一些安全隐患,例如混沌区存在一些空白窗,而且这些空白窗口与初始值无关,即无论选取什么样的初始值x0,空白窗都会存在。如图2所示,空白窗口出现在u=3.829的附近,在这些窗口中产生的序列只有少数的几个值,由此得到的序列没有随机性,而是几个确定的数值,用“空白窗”区间的序列来加密,系统没有任何安全性[5],因此加密时必须避开“空白窗”。

Logistic方程的另一个缺点就是,在Logistic方程的混沌区间3.569 945 67＜u≤4,如果分支参数u不等于4,那么得到的混沌序列就不会均匀分布在[0,1]区间,有的值无法取到,系统也就不存在遍历性,例如,由图2可知,如果选取分支参数u=3.75,无论经过多少次迭代计算,都不可能得到xn=0.1的值。要获得在[0,1]区间具有良好的随机性和遍历性的混沌序列,那么就只有选取根分支参数u=4.0,但是这等于是把密钥告诉了攻击者,使得加密算法失去了意义,因而加密者有必要设计一种更加优越的混沌方程。

2 广义Logistic方程及其分析

在经典Logistic方程的基础上研究广义Logistic方程[6]

其中参数的选择范围为:m∈Z,n∈Z,0＜xi＜1。

首先分析k的变化范围。因为f'(x)=kxm-1(1-x)n-1[m(1-x) -nx],f'(x)在区间[0,1]内仅存在1个零点,故f(x)在该区间内为单峰函数,且峰值为最大值。

为得到系统精确的分岔图,曾有人采用K均值聚类算法提取迭代数据中获得系统收敛的解[7],聚类的计算量非常大,而且算法复杂,并且当分岔解的个数增加时,聚类数以2的幂次增加,如果需要获得一定的精度,则需要很大的样本空间,聚类法其实并不适用于求解混沌系统的精确分插图。

以下计算特定的m和n参数下广义Logistic方程的Feigenbaum第一常数,从理论上证明广义Logistic方程同样具有混沌特性。注意到计算Feigenbaum第一常数,并不需要把所有分岔点对应的x,k值计算出来,进而注意到在分岔点处,x对k的斜率存在突变,因此选择分岔点处的k值即可,而经过足够次迭代后迭代数据中的xmax是容易计算的。实验证明系统在分岔点处存在比较明显的变化,当分岔点增多时,需要对k值作更加细致的研究。最后得到的经典Logistic方程以及m=2,n=1时的广义Logistic方程在各分岔点处的k值,迭代关系式为xi+1=kx2(1-xi)从而得出 Feigenbaum第一常数,数据如表1所示。

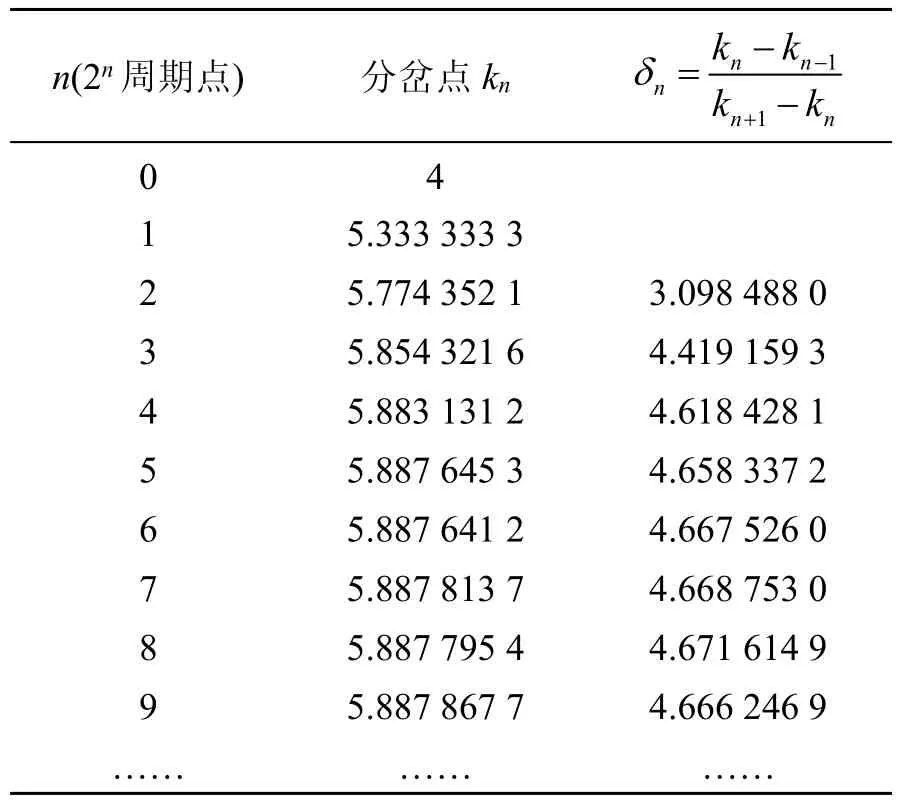
表1 Feigenbaum第一常数(m=2,n=1)

由表1可知,广义Logistic关系式[8]xi+1=kx2(1-xi)的Feigenbaum第一常数趋近于4.6(本研究暂时只讨论特定m值和n值下广义Logistic的混沌特性,并不需要研究该方程的Feigenbaum常数的精确值,所以这里只给出一个近似值)。

标准Logistic方程以及m=1,n=2时的广义Logistic方程各分岔点处的k值,迭代关系式为:xi+1=kx(1-xi)2得出的Feigenbaum第一常数如表2所示。

表2 Feigenbaum第一常数(m=1,n=2)

由表2可知,当迭代关系式为xi+1=kx(1-xi)2时,Feigenbaum第一常数趋近于4.6(由于计算时精度的选取关系,所以结果只是1个近似值)。

3 二维广义Logistic方程及其不动点分析

在广义Logistic方程的基础上,将二维广义Logistic混沌方程改进为

其中:x∈(0,1),y∈(0,1),n∈Z,u1=u2=u∈[0,1.2],r∈(0,1),其动力学行为是由u1,u2,r1,r2以及初始值x0和y0这6个控制参数所决定的。通过选取不同的控制参数组合,对系统的动力学行为进行全面的考察。如图3所示,纵坐标表示输出序列分布y的取值范围,分岔参数u的取值范围用横坐标表示,参数u的取值区间为[0,1.2],初始值x1=0.10,y1=0.11,r1=r2=0.1。

同理用纵坐标表示输出序列分布x的取值范围,分岔参数u的取值范围用横坐标表示,参数u取值区间为[0,1.2],初始值选取x1=0.10,y1=0.11,迭代计算后的分岔图如图4所示。

通过对二维广义Logistic方程的研究和实验,可知从整体上来说二维广义Logistic方程得到的分岔图和Logistic方程结构很相似,它具有经典Logistic方程应有的特性。从局部来看,二维广义Logistic方程的混沌区间发生了很大的变化,如参数u的取值范围就发生了很大的变化,二维广义Logistic方程比经典Logistic方程更加优越。更重要的是二维广义Logistic方程混沌区的混沌密度更高,且空隙距离缩小,二维广义Logistic方程的迭代图如图5所示。

为了在控制参数空间对二维广义Logistic方程的演化行为进行全面的研究,本研究选择性地选取不同的参数,作出二维广义Logistic方程的相图(见图6),第一条轨迹线为u1=u2=u∈[0.2,1.0]选取的初始点,当u=0.2时,系统趋向于相平面的一个稳定不动的点;随着r的增大,当u=0.3时,相平面出现了2个稳定的不动点。而当u=0.888时,2个不动点失稳,新的稳定状态围绕着原有的2个点演变为4条曲线(图6(a));u=0.92时,4条曲线演变为一条不规则的开口曲线(图6(b));u=0.95时,进一步变化,相平面演化成奇怪吸引子(图6(c));吸引子是描述运动的收敛类型,也就是当时间趋向于无穷大时,系统出发的非定常流的所有轨道都趋于某个稳定的范围(这种范围有复杂的几何结构)。随着u的不断增大到0.99时,系统又出现稳定的不动点(图6(d)),但是这些不动点数量较多,也就是说,给系统一个初始值x1,系统最后都会收敛到这些点上,或者说系统是一个多周期函数,这个函数的周期数就是这些不动点的个数;当u=1.0时系统出现越界,数值变得不可控,也不可预测。

图7、8、9是用相空间重构法的描述的二维广义Logistic方程的奇怪吸引子[9]。

由图6～9得到二维广义Logistic方程的奇怪吸引子的特点:

(1)从整体来看,二维广义Logistic方程系统是稳定的,吸引子外的一切运动最后都会收敛到吸引子内部,而内部吸引子的运动是不稳定的,类似于混沌;

(2)奇怪吸引子不一定都是集中的,有一些是分散的,或者稀疏的分布。从而这些奇怪吸引子具有无穷层次的机构相似性;

(3)由二维广义Logistic方程xn/xn+1=f(x)=xn/[uxn(1 -xn)]得到u(1 -xn),当,由此得到的是一个一元二次方程,即开口向下的抛物线。如图7所示。

通过理论分析和实验仿真得到如下的结论,当控制参数u1,u2相差较大,得到的结果大有区别。研究u1=0.72,u2=0.28且r∈(0.1,0.75)时二维广义Logistic方程系统行为的演化规律,二维广义Logistic方程的迭代分岔图如图10、11所示。当u1=0.8,u2=0.2、且r∈[0,0.6]时系统行为演变规律,如图12、13所示。

4 分段映射与仿真

分段线性映射是一种一维映射,这里通过对一般分段线性映射进行有效改进,得到如下的分段余弦函数(Piecewise cosine chaotic map,PCCM)[10],该方程为

其中,yn为初始混沌的序列值,且yn∈(0,1);t为系统的控制参数,并且t∈(0,0.5)。仿真实验证明,这种改进后的分段余弦映射具有很好的混沌特性和复杂的动力学行为。

通常可以使用序列的互相关函数进行量化分析,用来衡量混沌序列的性能优劣。当互相关函数值越小,表明被测序列的伪随机性越好。互相关函数的定义为

其中,xk、yk是在二元域[-1,1]上长度为p的2个混沌序列。

互相关性的分析是指在混沌方程中参数x1,r,u,y1等系统初值作微小的变化情况下,序列的相似度。如果互相关性越小,说明其混沌序列更好,反之则越差。

取初值u=3.9,x1=0.1和初值x1=0.1+10-15,利用Logistic方程进行迭代计算,分别生成2个具有1 000个迭代值的混沌序列,对这2个序列进行互相关性实验测试,并将测试的结果以图像的形式直观表示,结果如图14所示,经典Logistic混沌方程生成的混沌具有较小的互相关性,其相关性系数在0.35左右,因此经典Logistic方程生成的混沌序列具有较好的伪随机性。

取2组初值:u=0.958,x1=0.10,y1=0.11,r=0.1和x2=0.10+10-15,y2=0.10+10-15时,利用二维广义Logistic方程进行迭代计算,分别生成2个具有1 000个迭代值的混沌序列,对这2个序列进行互相关性实验测试,用来量化分析二维广义Logistic方程的性质,实验仿真结果如图15、16所示。

由图15可知,二维广义Logistic混沌方程生成的x1与x2序列的互相关性比较小,其相关性系数基本在0.22左右,因此二维广义Logistic方程生成的代表x向量的混沌序列具有良好的伪随机性。

由图16可知,二维广义Logistic混沌方程生成的y1和y2的互相关性也比较小,其相关性系数基本在0.004 8左右,因此二维广义Logistic方程生成的代表y向量的混沌序列也具有很好的伪随机性。

由式(1)、(3)的结果可知,二维广义Logistic混沌方程不管从x序列或者y序列方面来看,其互相性关系数均小于传统Logistic混沌方程的互相关性系数,可以说明,由二维广义Logistic方程生成的混沌序列比由经典Logistic方程生成的混沌具有更好的伪随机性。

由二维广义Logistic方程方程生成混沌序列,其中取初值x1=0.10,y1=0.11,r1=0.1,u=0.958,经过迭代65 536次得到y序列,然后取y序列的值代入式(4)进行分段计算,其分段余弦映射(Piecewise cosine chaotic map,PCCM)方程式(4)中的t=0.4。结果见表3。

表3 分段前后的序列信息

上述仿真结果证明,二维广义Logistic方程生成的混沌序列本身比经典Logistic方程生成的混沌序列优越,再通过分段映射方程对其混沌序列进一步的优化,这样就有利于混沌序列的又一次随机变化,由二维广义Logistic方程生成的混沌序列经过上述的优化,更加有利于图像加密。