基于虚拟阻抗与无源反步控制的MMC-BESS环流抑制策略

孔凡森，周建萍，茅大钧，周安杰，李逸凡

(上海电力大学自动化工程学院，上海 200090)

0 引言

近年来，光伏、风能等大规模可再生能源并网应用逐渐成为一种趋势[1 - 2]，但是也加剧了电网的功率波动，对现代电力系统提出了新的挑战[3 - 5]。为了减轻可再生能源的随机性和间歇性对电力系统带来的冲击，基于模块化多电平的电池储能系统(modular multilevel converter with integrated battery energy storage system，MMC-BESS) 应运而生[6 - 8]。凭借模块化程度高，易于拓展，灵活调节电压等优点，MMC-BESS得到了广泛研究[9 - 11]。但是MMC-BESS存在的环流会导致输出电压畸变，产生谐波影响电能质量；增加损耗，导致开关管发热，影响装置使用寿命[12 - 13]。因此抑制MMC-BESS桥臂环流显得十分重要[14 - 15]。

文献[16 - 17]提出了MMC的小信号模型建立与分析方法，对于系统的稳定性运行与控制具有重要意义。文献[18 - 19]介绍了几种MMC拓扑结构与通用的分析控制方法，将环流通过abc-dq坐标变换，dq轴的输出分量便于控制，抑制环流。文献[20]提出了比例谐振(proportional resonant，PR)加桥臂电流负反馈的控制方法，快速抑制环流，但是易受外部干扰影响，导致误差增大。文献[21]采用重复控制实现对环流的抑制，并加入PI控制，提高系统的响应速度，提升了动态性能，但控制精度较差。文献[22]应用了模型预测控制，来抑制二倍频环流和电容电压波动，鲁棒性强，控制简单，但计算量大，参数调制复杂。文献[23]提出了滑模控制(sliding mode control，SMC)方法并应用到MMC-STATCOM中，对MMC系统环流有着良好的抑制效果，但动态性能有待改进，且没有研究应用于三相系统之中。文献[24]将反步控制(backstepping control, BSC)应用于MMC环流抑制，体现出其控制跟踪速度快，暂态性能优异，但是控制精度不足。文献[25]建立了基于无源控制(passivity-based control, PBC)的MMC系统模型，采用正负序分离的方法，取得了良好的控制效果。文献[26]建立了基于端口受控耗散哈密顿系统的MMC模型，提出了无源反步的复合控制方法，兼顾了控制精度与响应速度，提升了系统鲁棒性，但没有考虑环流高次谐波。文献[27]建立了基于状态反馈精确线性化解耦的环流模型，运用了虚拟阻抗滑模控制抑制二倍频环流，取得了较好的效果，提升了系统稳定性。以上的非线性控制在MMC环流应用中已经得到验证，但是值得注意的是，这些控制均没有考虑环流中的高次谐波问题，但是在MMC-BESS系统中不应忽略。

综上所述，为了抑制 MMC-BESS的桥臂环流，本文建立基于EL模型的环流系统，提出了基于虚拟阻抗与无源反步控制(virtual impedance and passive back-stepping control, VI-PBSC)相结合的环流抑制策略。所提控制方法不仅能够保证系统满足全局稳定性，而且能够有效抑制环流二倍频分量，在外部扰动下，快速追踪参考值，动态性能好，鲁棒性强，此外还对环流高次谐波分量进行抑制。最后，通过MATLAB/Simulink仿真验证了所用方法的优越性。

1 MMC-BESS拓扑与数学模型

1.1 MMC-BESS拓扑结构

三相MMC-BESS的拓扑及其子模块结构如图1所示。每条支路含有2N个子模块，又分成上、下两个桥臂，N表示每个桥臂的串联子模块数。在本文中，下标k=(a, b, c)为相位；j=(p, n)分别代表上、下桥臂；i=(1, 2，…，N)为桥臂内的单个子模块。直流侧电压和相电压分别表示为Udc和Ujk。每个桥臂包含一个桥臂电感Lm，桥臂等效电阻Rm。

图1 三相MMC-BESS及其子模块结构图Fig.1 Configuration of MMC-BESS and its sub-modules

总体而言，MMC-BESS的拓扑结构与传统MMC一致。主要区别在于子模块的拓扑结构，除了采用半桥结构外，储能单元以不同的方式集成到每个子模块中，形成如图1所示的两种类型的子模块结构。对于SM-A型，电池直接连接到单个SM电容的两端上，此结构强迫电容电压跟随电池电压，会引起功率波动，损害电池寿命。SM-B型由DC/DC接口连接电容和储能单元，通过适当的控制策略，可以防止纹波流入电池，但同时也会降低转换效率。所以本文采用SM-B型子模块结构。

1.2 MMC-BESS环流EL模型

如图1所示，上、下桥臂电压可以等效为Upj、Unj，桥臂电流用ipj、inj表示，每相桥臂电流为：

(1)

式中：isj为交流侧相电流；izj为每相环流。

通过KVL可以建立MMC的内部电压电流特征方程，可以得到环流压降，即环流流过每个桥臂电抗产生压降

(2)

其值也可表示为

(3)

忽略高次分量，仅考虑环流直流分量和二倍频分量，则环流可表示为

(4)

式中：Idc为直流侧电流幅值；icirj为j相环流二倍频分量。

为了便于对环流分量的控制，将式(4)进行abc-dq变换。其变换矩阵为

(5)

将式(4)代入式(2)中并通过坐标变换，可得dq坐标系下的MMC内部电压电流特征方程为

(6)

式中：ucird和ucirq分别dq轴坐标系下的二倍频环流压降；icird和icirq分别dq轴坐标系下的二倍频环流。MMC相间环流的EL模型为

(7)

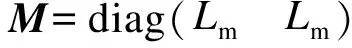
1.3 MMC-BESS环流EL模型无源性分析

假设在某系统中，V(x)为该系统的能量存储函数，Q(x)为该系统的正定函数，对任意T>0，满足以下的式(8)的耗散不等式，说明该系统是无源的。

(8)

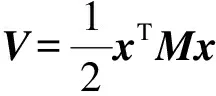
(9)

令y=x，正定函数Q(x)=xTRx， 则式(9)恒满足式(8)，MMC-BESS环流模型具有无源性。

2 环流VI-PBSC控制器设计

2.1 无源控制器设计

当MMC-BESS稳定运行时，由式(7)可得：

(10)

取误差能量函数为：

(11)

对式(11)求导：

(12)

Rdxe=(R+Ra)xe

(13)

式中Rd为系统注入阻尼后的正定矩阵。

将式(13)代入式(10)可得：

(14)

选取无源控制律：

(15)

将式(14)、式(15)代入式 (12)，可得：

(16)

联立式(6)、式(7)、式(15)，可以得到MMC-BESS环流无源控制器的控制规律：

(17)

2.2 无源反步控制器设计

MMC-BESS 环流无源控制器设计过程中一定程度上牺牲了对系统控制量的快速跟踪能力，所以加入反步控制来提升系统的动态响应性能。

将式(6)改写为

(18)

式中x1=icird；x2=icirq；a1=-Rm/Lm；a2=1/Lm。

设dq轴的环流误差为

(19)

对式(19)求导可得：

(20)

(21)

引入线性量k1z1、k2z2，提升系统的动态响应性能。定义环流控制量ucird、ucirq的值为：

(22)

式中：k1、k2为反馈增益，均大于0。最终得到MMC-BESS环流反步控制律为：

(23)

联立式(17)和式(23)可得基于EL模型的 MMC-BESS 环流无源反步控制律为

(24)

由式(24)可得基于EL模型的MMC-BESS无源反步环流控制器结构框图，如图2所示。

图2 无源反步环流抑制器示意图Fig.2 Diagram of the passivity-based backstepping circulating current suppression

2.3 附加虚拟阻抗设计

在传统MMC中，环流中高次谐波含量较少，在设计环流控制器中通常忽略不计。但是在MMC-BESS结构中，由于储能单元是分布式地集成在子模块中，通过DC/DC变换器与MMC连接，采用适当的控制方法可以隔绝大部分的纹波电流，但仍有小部分的高次谐波进入桥臂之中，需要对这部分高次谐波电流加以抑制。

针对桥臂中的高次谐波电流，有文献采用PR控制对特定频次的环流进行抑制，但是需要的控制器较多且和无源反步控制互相干扰，系统的控制精度下降。而虚拟阻抗不仅等效增加桥臂电抗，抑制高次谐波电流，还能分担无源反步控制中的二倍频环流抑制，避免因注入电阻过大引起的功率损耗问题。

图3(a)为虚拟电阻Rv和虚拟电抗Lv并联组成的虚拟阻抗。图3(b)为d轴附加虚拟阻抗控制，经过虚拟阻抗的压降修正量，与无源反步控制器的输出量组成d轴电压控制量，q轴电压控制量同理即可得出。最终修正方程为：

图3 附加虚拟阻抗控制Fig.3 Additional virtual impedance control

(25)

2.4 VI-PBSC控制器设计

综上所述，联立式(24)、式(25) 和图3可得基于EL模型的MMC-BESS 环流虚拟阻抗与无源反步控制框图，如图4所示。

图4 MMC-BESS整体控制框图Fig.4 Overall block diagram of MMC-BESS

3 环流VI-PBSC控制器设计

3.1 稳态运行下仿真运行分析

为验证基于EL模型的MMC-BESS的虚拟阻抗与无源反步环流控制策略的可行性，本文在Matlab/Simulink中，分别建立传统PI控制、无源控制(PBC)、反步控制(BSC)、无源反步控制(PBSC)和本文所提虚拟阻抗与无源反步控制(VI-PBSC)的五种仿真模型。稳态条件下，系统运行的仿真参数如表1所示。

针对桥臂环流的不同控制方法，本文均已调至最佳运行状态，此时各环流抑制策略的控制参数如表2所示。

表1 MMC-BESS系统仿真参数Tab.1 Parameters of the MMC-BESS system

表2 MMC-BESS各环流抑制策略控制参数Tab.2 Control parameters of the MMC-BESS CCSCs

系统在0.5 s时启动环流抑制，可以得到直流侧电压、电流波形图，交流侧电压电流波形图，a相上、下桥臂电流图与a相环流图等，具体波形如图5所示。

图5 稳态下VI-PBSC的仿真波形Fig.5 Waveforms of VI-passive and back-stepping circulating current suppression under steady state

稳态运行下的直流侧电压、电流如图5(a)所示，仿真在0.5 s时加入环流控制器。环流控制器接入主电路后，并未对直流侧产生扰动，没有发生电压电流脉动情况，通过抑制二倍频环流，提升了系统的稳定性；由图5(b)可知，MMC-BESS环流不影响交流侧输出外特性，系统运行平稳；由图5(c)可知，a相上、下桥臂电流幅值在400 A左右，波形接近标准正弦波；由图5(d)可知，a相环流在0.5 s前，上下峰谷差达到8 A，环流抑制器投入后，环流基本稳定在10 A，波动很小。

不失一般性地将三相环流中的a相用作分析，图6(a)为5种不同控制下a相环流的波形图，可以看到在加入环流控制器之前，相间存在较大环流，主要以二倍频环流为主，会产生较大损耗。图6(b)为5种模型下a相环流FFT分析图，可以直观地看到环流中的谐波含量(以直流量为基准)。系统在0.5 s时加入环流抑制器，通过图6可以分析5种控制在稳态下对环流的抑制能力。PI控制抑制能力有限，且会产生尖峰毛刺，效果最差，直流损耗最大，THD值为7.83%；PBC环流抑制器得益于注入阻尼的影响，对二倍频环流有着较强的抑制效果，但环流波形仍然有较大波动，直流损耗也较大，THD值为5.28%；BSC抑制器的环流波形与PBC波形接近，但直流损耗较无源控制有所降低，THD值为4.59%；PBSC环流抑制器综合前两者的优点，进一步提升了抑制能力，抑制环流的效果较好，直流损耗量较大程度降低，THD值也降低到了3.18%；VI-PBSC抑制器不仅针对二倍频环流，且对高次谐波同样进行抑制，所以其波形更加平稳，基本在Idc/3处上下波动，波动幅值最小，抑制效果最好，同时，虚拟阻抗替代了部分注入电阻的作用，进一步降低了直流损耗，THD值仅为1.73%。因此，可以验证VI-PBSC环流抑制器能够使系统有效降低环流二次及以上谐波影响，减小系统损耗。

图6 5种模型下a相环流及FFT分析Fig.6 Phase-a circulating current waveform and FFT analysis under five different models

3.2 有功功率突变时仿真运行分析

如图7(a)所示，初始设置 MMC-BESS并网控制回路有功功率参考值2 MW，无功功率参考值为0 Mvar；仿真时间到达0.5 s时加入环流抑制器；仿真时间在1 s时有功功率参考值由2 MW突增至3 MW，无功功率参考值保持不变；仿真时间在1.5 s时有功功率参考值突降至2 MW，无功功率参考值保持不变。

有功功率突变时，5种不同控制下a相环流变化如图7(b)所示。整体过程来看，基于VI-PBSC的抑制器的环流波动最小，受抑制程度最高；PI控制波动最大，抑制效果最差；PBC、BSC和PBSC环流抑制系统同样产生较大程度的波动情况。在1 s时有功突增，通过局部放大图可以看到，基于VI-PBSC环流波形最先到达稳定值，且没有过大超调，动态响应速度最快，其余4种控制都有明显的超调。同样在1.5 s有功功率突降时，基于VI-PBSC和PBSC环流控制系统响应速度最快，但PBSC波形存在明显的超调，VI-PBSC的动态性能更为出色。因此，基于EL模型的VI-PBSC环流抑制方法，在有功功率突变时，不仅响应速度快，超调小，且环流抑制能力更加出色，抗干扰能力更强，证明了VI-PBSC控制方法的动态性能优越性。

图7 5种模型有功功率突变时a相环流示意图Fig.7 Phase-a circulating current waveform of five different models with power mutation

3.3 负载突变时仿真运行分析

如图8(a)所示，初始设置负载电阻20 Ω，负载电感20 mH。在0.5 s时加入环流抑制器，1 s时负载突降20%，即此时负载电阻16 Ω，负载电感16 mH；1.5 s恢复初始值，其余参数保持不变。

负载突变时，5种不同控制下a相环流变化如图8(b)所示。整体过程来看，在1 s和1.5 s负载突变时，环流迅速跟踪变化，其中基于VI-PBSC抑制器的环流波动最小，进入稳态后抑制能力最强；PI控制由于整定参数无法变化，抑制效果最差，环流波动最大；PBC、BSC和PBSC环流波形都存在较大的稳态误差和波动。通过局部放大图可以看到，在1 s负载突降时，PI控制超调过大；PBC和BSC环流抑制器能够实现渐进跟踪，但波形存在明显超调；PBSC环流反应速度较快，但高次谐波造成的波动明显；基于VI-PBSC抑制器响应速度快，最先到达稳定值，超调小，稳定后环流抑制能力强，波动小。同样在1.5 s负载突增时，基于VI-PBSC的环流抑制器同样比其余4种控制动态性能强。因此，在系统外部参数发生变化时，基于EL模型的VI-PBSC抑制器具有抗干扰能力强，环流抑制能力好，响应速度快，超调小的优点，证明了VI-PBSC环流抑制策略的动态性能优越性。

图8 5种模型负载突变时a相环流示意图Fig.8 Phase-a circulating current waveform of five different models with load impedance mutation

3.4 直流侧电压突变时仿真运行分析

如图9(a)所示，初始设置直流侧电压6 000 V。在0.5 s时加入环流抑制器，1 s时电压突降10%，即此时直流电压为5 400 V；1.5 s恢复初始值，其余参数保持不变。

图9 5种模型直流电压突变时a相环流示意图Fig.9 Phase-a circulating current waveform of five different models with dc voltage mutation

直流电压突变时，5种不同控制下a相环流变化如图9(b)所示。从整体过程并结合局部放大图来看，在1 s和1.5 s直流电压突变时，VI-PBSC环流抑制器跟踪变化的速度最快，且到达稳态时波形最为平稳；PI控制存在较大超调，波形波动最大；PBC、BSC和PBSC环流波形在稳态时存在明显波动，抑制效果不如VI-PBSC，且动态反应速度稍差。在直流电压发生突变时，不管是环流抑制效果还是动态反应性能，基于VI-PBSC的环流抑制器都优于其余四种控制。

4 结论

针对MMC-BESS自身非线性特性，以及在运行过程中电容电压不均衡导致的环流问题，本文提出了基于EL模型的VI-PBSC环流抑制策略。结论如下。

1)该方法推导MMC-BESS无源控制律方程，调整能量函数，修正控制参数，确保系统满足Lyapunov稳定性定理；加入反步控制实现环流二倍频分量渐进跟踪，具有良好的动态性能；加入虚拟阻抗并行控制，抑制环流中的高次谐波分量，分担无源反步控制的环流二倍频抑制，减小系统损耗。

2)通过五种控制方法的建模仿真对比，结果证明了VI-PBSC环流控制策略显著降低了环流谐波分量，且超调小，响应速度快，提升了系统鲁棒性，有利于系统稳定、可靠运行。