基于强度折减法的伯斯阿木水库边坡稳定性分析

鲁克恩

（新疆维吾尔自治区水利水电勘测设计研究院有限责任公司，新疆 乌鲁木齐，830000）

1 工程概况

伯斯阿木水库工程位于新疆维吾尔自治区和硕县境内的清水河上，是一座具有灌溉、防洪等综合效益的水利工程。工程由拦河坝、表孔溢洪洞、深孔泄洪洞（导流洞改建）和灌溉放水洞等组成。水道建筑物联合进口边坡走向约300°～315°，闸井后边坡高陡，自然坡度65°左右，基岩裸露，岩性为大理岩，属中硬岩，基岩强风化层厚 2～3m，弱风化层厚 10～12m，岩层产状 305°～310°NE∠70°。总体来看，进口边坡高陡，岩体较完整，边坡整体稳定。另外，进口边坡为顺向坡，层理与进口边坡近平行。

联合进口段岩体临时设计开挖边坡为1:0.3，永久设计开挖边坡为1:0.5，每10m设一马道，马道宽2m。表孔溢洪洞闸室段两侧岩体直挖，闸井平台高程1 487.50m（1985国家基准高程，下同）至岩体高程1 557.50m，设计开挖边坡为1：0.5，每10m设一马道，马道宽2m。导流兼深孔泄洪洞和灌溉放水洞闸井两侧岩体高程1 423m以下岩体设计开挖边坡为1：0，每10m设一马道，马道宽2m，高程1 423～1 433m之间岩体设计开挖边坡为1：0.3，高程1 433m以上岩体设计开挖边坡为1：0.5，每10m设一马道，马道宽2m。截面如图1所示。

图1 边坡剖面图

边坡岩土体的成分主要是大理岩，由弱风化线分化成两部分，其力学参数如表1所示。

表1 岩体力学参数

2 强度折减法

2.1 边坡稳定的研究方法

当前，对边坡稳定性分析研究使用较多的方法有刚体极限平衡法和强度折减法。由于刚体极限平衡法需要预先假定滑动面，所以本文未采用。强度折减法以边坡的力学特性为强度储备，逐渐降低岩土体的力学特性并进行相应的数值计算，当数值计算显示失稳时，力学特性折减的倍数即为安全系数。强度折减法适应性较好，能够计算复杂地质条件下的边坡稳定性，且不需要假定滑动面。强度折减法最早由Zienkiewicz[1]提出，由于当时计算机技术的限制，未被大规模采用，后来随着数值算法改进和计算机技术的发展，该方法被大规模应用到边坡的稳定性研究中。国内不少学者也对强度折减法进行了相应研究，郑颖人[2-4]提出摩尔-库伦等面积圆屈服准则，并在土坡和岩质边坡中应用。连镇营[5]用强度折减有限元方法对开挖边坡的稳定性进行了较为全面的研究，认为弹性模量、泊松比、剪胀角和侧压力系数对边坡的安全系数影响不大。姜庆飞[3]提出了一种主动岩层组合式局部强度折减法，对三层边坡进行局部强度折减和全局折减分析，加固后坡体稳定性明显提高。陈愿成[6]提出了考虑残余强度的动态强度双折减系数法，实现了对边坡潜在滑带的拓展过程模拟。本文基于ansys软件，使用强度折减法对此工程进行稳定性分析。

2.2 强度折减法的基本原理

根据M-C屈服准则，作用在斜截面上剪应力与正应力的关系为：

式中，c是黏聚力；φ是内摩擦角；τ为剪切面的抗剪强度；σn为剪切面的正应力。

岩土体发生的破坏大多以剪切破坏为主，强度折减的材料强度以抗剪强度为主即[7，8]：

式中，F为材料的强度折减系数；τ′为折减后抗剪强度。

将公式（2）做相应处理，得到

式中，c′为折减后的黏聚力；φ′为折减后的内摩擦角。

强度折减法的失稳判别方法主要有三种：（1）数值计算未能收敛；（2）滑块体某特征点的计算位移较之前折减系数下的计算位移有明显突变；（3）塑性区发生贯通，贯通区域一侧为滑动面。对于边坡失稳的判别方式，不同学者持有不同态度。赵尚毅[9]认为塑性区贯通是破坏的必要条件，但不是充分条件；刘金龙[10]、栾茂田[11]认为有限元计算的数值收敛性受多种因素的影响，因而由此所得到的安全系数的合理性及其唯一性受到了质疑。基于失稳判定的不确定性，本文对不同的边坡失稳判据进行了对比分析。

3 天然及开挖工况的稳定性分析

3.1 计算模型

建立有限元计算模型如图2所示，总共剖分成4 124个单元，单元主要以四边形单元为主，同时也含有少量三角形单元。

图2 边坡有限元计算模型

3.2 边坡塑性区扩展

3.2.1 天然工况塑性区扩展

天然工况计算得到的塑性区如图3所示，随着折减系数的增大，塑性区也随之增大。折减系数从1.0增大到1.80时，边坡无塑性区。当折减系数增大到1.85时，在坡角处产生塑性区；随着折减系数的增大，塑性区向后发展；当折减系数增大到2.10时，塑性区的宽度也有所增大；折减系数增大到2.18时，塑性区接近贯通，计算也未收敛。

图3 天然工况塑性区图

3.2.2 开挖工况塑性区扩展

开挖工况计算得到的塑性区如图4所示，随着折减系数的增大，塑性区也随之增大。折减系数从1.0增大到1.80时，边坡无塑性区。当折减系数增大到1.80时，在坡角处产生塑性区；随着折减系数的增大，塑性区向后发展；当折减系数增大到2.00时，塑性区的宽度也有所增大；折减系数增大到2.09时，塑性区接近贯通，计算未收敛。

3.3 失稳判据分析

从图3和图4可知，塑性区在计算不收敛之前未达到贯通，由于有限元计算不收敛的因素有很多，计算不收敛不能说明边坡已经失稳，因此，本文引入位移突变的失稳判据，以证实边坡达到失稳。天然工况和开挖工况两种工况下某特征点位移随折减系数变化曲线如图5所示。

图4 开挖工况塑性区图

图5 位移随折减系数变化规律

由 5（a）和 5（b）可知，随着折减系数增大，位移前期变化较小，后期变化较大。两种工况下，当折减系数增大到2.18和2.09时，位移相比于上一次有明显变化，同时计算也未收敛。即计算不收敛和位移突变同时发生，在本工程的计算中，位移突变为失稳依据和计算不收敛具有一致性，即在位移突变时，有限元程序无法从有限元方程组中找到一个既能满足静力平衡又能满足应力-应变关系和强度准则的解，计算无法收敛。虽然有限元计算的收敛性受到很多因素的影响，但将计算不收敛和位移突变两种判据同时考虑，其准确性会提高。

在计算不收敛时，塑性区仍未贯通，但位移已经有明显的突变，说明在底部塑性区两侧已经开始产生相对滑动，从而导致边坡局部失稳。塑性区贯通的失稳判据在边坡局部破坏中适用性较差。

3.4 开挖对边坡稳定的影响

通过塑性区得到最危险滑裂面，开挖前后的滑裂面如图6所示。天然工况的失稳特征和开挖工况的失稳特征一样，但是滑裂面有所不同。相较于天然工况，开挖工况下的最危险滑裂面较为陡峭，更加平直。开挖后的边坡安全系数为2.09，小于天然工况的2.18。文献[3]认为边坡角度越大，安全系数越小，本工程开挖工况边坡角度较天然工况大，所以开挖后的安全系数更小。

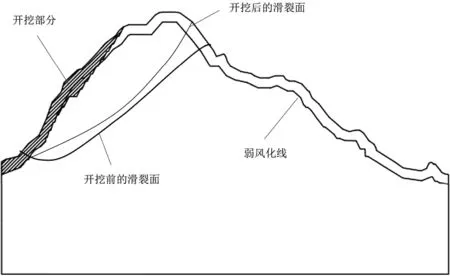
图6 天然工况和开挖工况最危险滑裂面

4 结语

（1）通过强度折减法的计算，伯斯阿木水库工程最危险的失稳方式为局部失稳而非整体失稳。天然工况的安全系数为2.18，开挖工况的安全系数为2.09，两种工况都满足稳定要求。

（2）两种工况下边坡的失稳特征一样，从该边坡的塑性区从坡脚开始，逐渐向上扩展，在塑性区扩展至贯通前已经全部失稳。

（3）开挖后，由于边坡的角度更大，安全系数变小，稳定性较差，最危险滑裂面也发生变化。由于开挖后边坡稳定性较差，建议做一些支护措施，例如施加预应力锚索。

（4）强度折减法的计算不收敛判据和位移突变判据具有一致性，两种方法相结合，计算得到的结果更加准确。塑性区贯通的失稳判据在局部失稳中并不适用。