基于坝基塑性损伤的重力坝极限抗震能力研究

田 晔，吴邦彬，周清勇，高 俊

（1.江西省安义县水利局，江西 安义，330500；2.南昌工程学院，江西 南昌，330099；3.江西省水利科学院，江西 南昌，330029；4.江西省南昌县联圩河道堤防中心，江西 南昌，330200）

0 引言

高坝震例和实测资料表明，地基岩体中由于微裂隙的存在，更易发生损伤和破坏，但目前进行重力坝数值仿真时，大多将坝基设为线弹性材料，仅考虑坝体的损伤破坏。Koyna坝作为混凝土重力坝遭受地震灾害的典型案例，众多学者对其进行数值分析时发现：若将地基设为线弹性材料，坝踵附近的混凝土会出现损伤破坏[1～3]。但实际震害显示Koyna重力坝坝踵附近混凝土并没有出现损伤破坏，这是由于将地基设为线弹性不能反映其真实损伤破坏情况所导致的[4]；徐金英、王星等[5]通过对比研究考虑坝基塑性损伤时和坝基线弹性时的鲁地拉重力坝极限抗震能力，结果发现：考虑坝基塑性损伤能明显减轻重力坝坝体损伤程度，可以更加真实的模拟出大坝的抗震承载能力。因此，考虑坝体-坝基整体损伤进行重力坝抗震研究十分有必要。为了更为实际地反映重力坝在遭受地震作用后的损伤破坏情况，本文利用Lee和Fenves[6]提出的塑性损伤模型，根据混凝土与岩体材料的相似性，将混凝土塑性损伤模型推广到岩体材料[7]。以我国西南某拟建混凝土重力坝为研究对象，建立了考虑坝体-坝基整体塑性损伤的三维有限元动力计算模型，并对模型的正确性进行了验证。采用时程分析法分析了该坝在不同地震强度下的震损情况，并以坝体裂缝贯通上下游为失稳判别标准对大坝的极限抗震能力进行了评价。

1 计算理论

1.1 混凝土塑性损伤理论

混凝土塑性损伤模型本构关系：

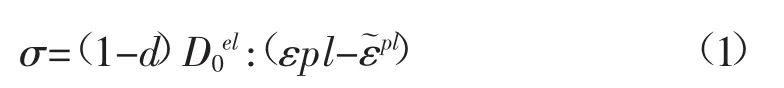
式中：σ 为应力；d为损伤变量（0≤d≤1）；ε 为应变；为塑性应变；D0el为无损弹性刚度。

损伤后的弹性模型表示为：

2 整体损伤模型的验证

为了证明本文所建重力坝-坝基整体损伤模型是正确的，将本文计算出的Koyna重力坝损伤破坏情况与前人的计算结果进行对比验证。Koyna重力坝坝高103m，坝基底部和坝顶宽分别为70.2m、14.8m，坝前水位91.75m。建立图1所示有限元模型。地基范围为：上、下游、深度方向地基各取1.5倍坝高。模型中防渗帷幕中心线距坝体上游面7m，帷幕深度为1/2坝前水位高度，取45.5m。坝体、坝基均设为塑性损伤材料。

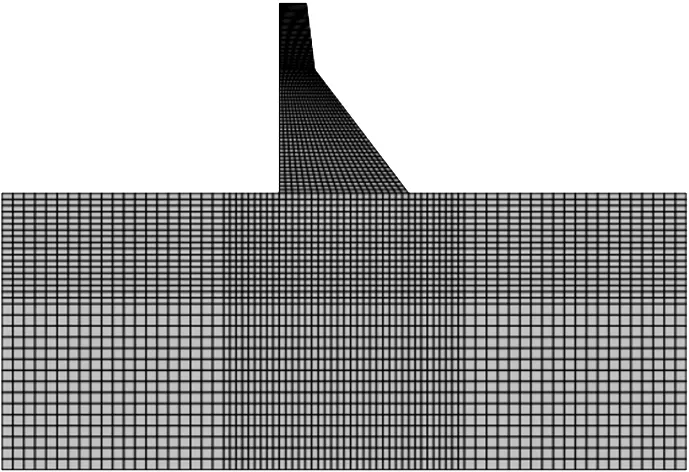
图1 Koyna重力坝有限元模型

计算采用的坝体混凝土、基岩材料参数见表1和表2，防渗帷幕取值与坝体混凝土相同。

表1 坝体混凝土材料属性

表2 基岩材料属性

同时输入水平向峰值加速度为0.474g和竖向峰值加速度为0.312g的Koyna实测地震波（如图2所示）。在截断边界处施加粘弹性人工边界[8]以防止地震波发生反射。

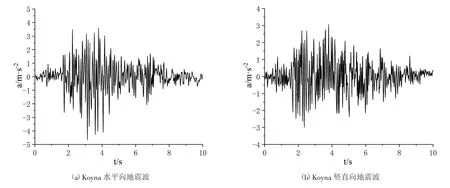
图2 Koyna实测地震波

图3给出了考虑坝基塑性损伤时，地震结束时的坝体损伤分布图。从图中可以看出，坝体在下游折坡处附近形成贯通上下游的裂缝，坝踵附近损伤区域主要位于坝基岩体并沿深度方向开展，坝踵处的混凝土并没有损伤开裂，而Koyna坝实际震害情况是震后并未发现坝踵出现拉裂，本文的数值仿真结果与实际相符[9]。将本文考虑坝体-坝基整体损伤下的Koyna坝损伤分布与文献[9]计算出的损伤分布情况（图4）进行对比，可以看出坝体均在折坡处附近形成贯通的裂缝，坝基损伤区域主要位于坝基岩体并沿深度方向开展，证明本文所建重力坝-坝基整体损伤模型的正确性。

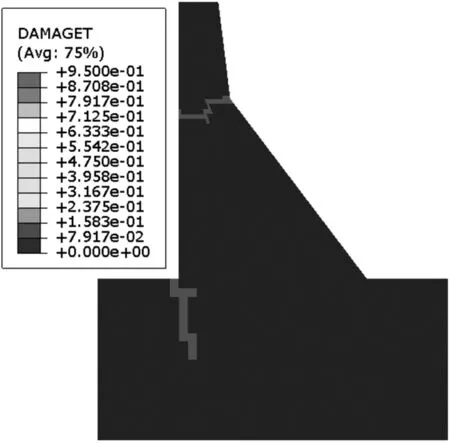
图3 Koyna坝体-坝基损伤分布图

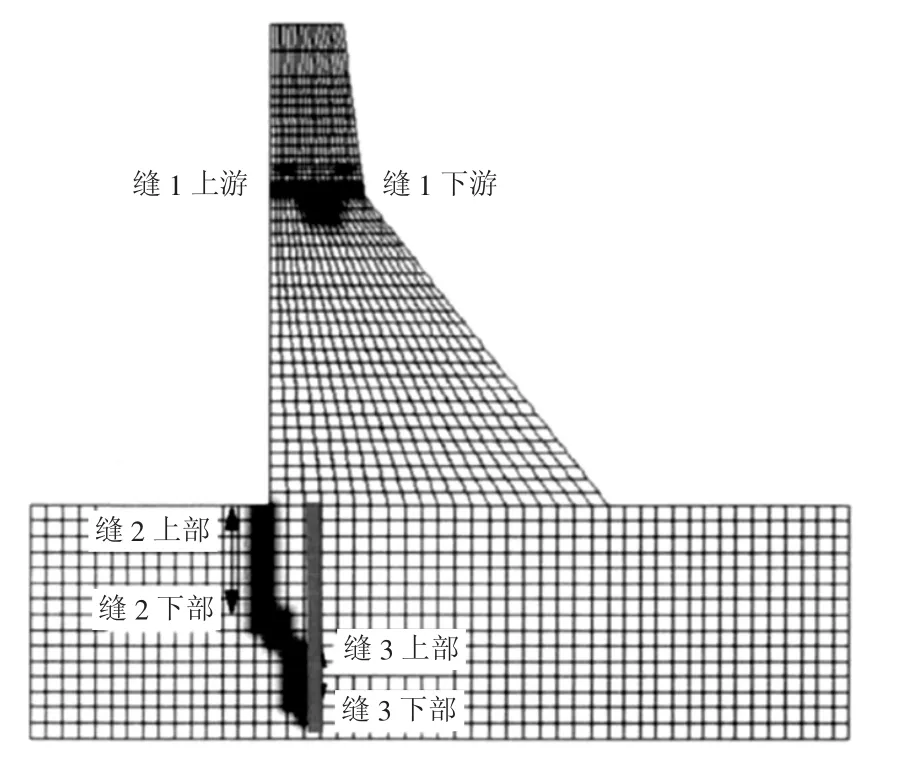
图4 文献[9]计算出的Koyna坝损伤分布情况

3 重力坝整体损伤模型的建立及抗震能力分析

3.1 工程概况及有限元模型

我国西南某拟建重力坝坝底高程2 339.00m（黄海高程，下同），坝顶高程2 481.00m，坝高142.00m，坝宽122.20m，坝段厚22.00m，正常蓄水位2 477m。坝段材料分区及有限元计算模型如图5、图6所示，坝体根据混凝土材料划分成4个分区，坝基根据岩层走向分层建模，坝基上、下游及其深度方向均取1.4倍坝高。坝体、坝基采用塑性损伤材料，基岩材料的损伤参数采用将混凝土损伤曲线对应岩体抗拉强度进行相应折减的方式来确定[7]。动水压力以Westergaard附加质量法施加。初始地应力场按工程岩体分级标准中关于初始应力场评估的规定，竖向地应力为岩体自重γh，水平向地应力取1.2γh[10]。计算中采用材料参数见表3。

图5 坝体与坝基关键点示意图

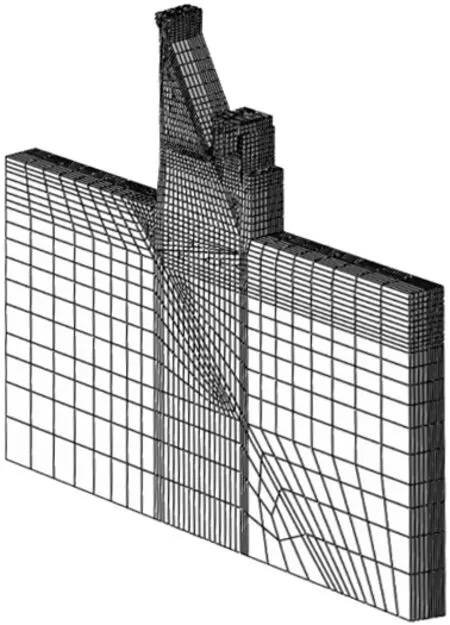
图6 三维有限元计算模型

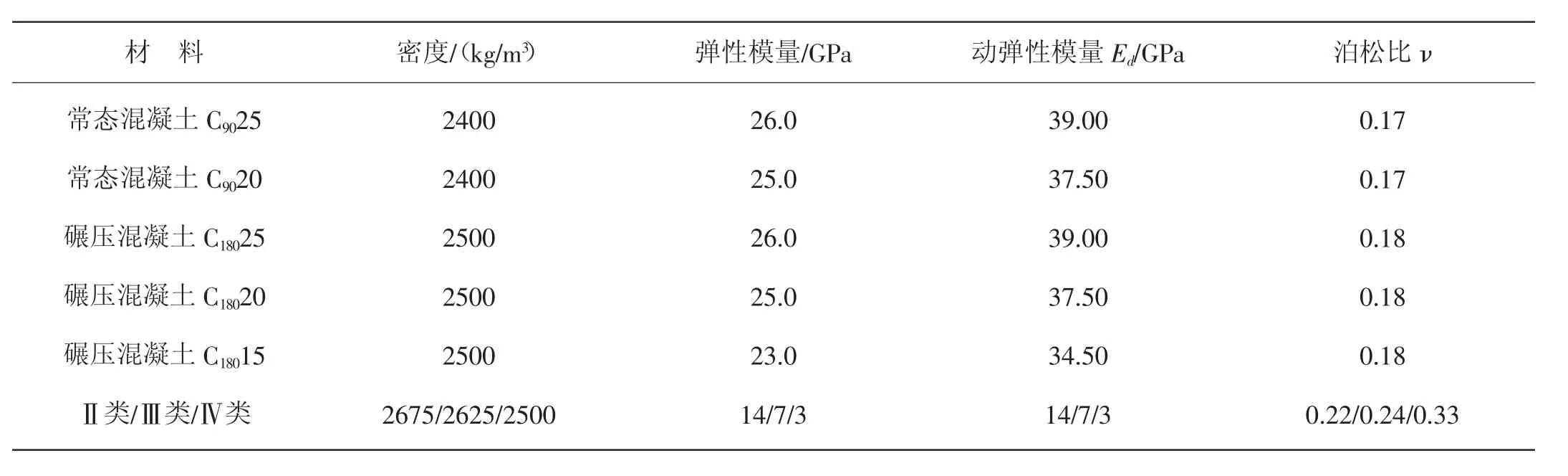
表3 材料参数表

本工程设计地震峰值加速度0.316g，校核地震峰值加速度0.3651g。根据场地反应谱合成图7所示的设计地震动时程曲线，水平向峰值加速度为0.316g，竖直向峰值加速度为0.211g，地震动持时为31s。为了使地震作用后的位移曲线趋于平稳，本文在有限元软件中设定动力分析步的总时长为35s。在截断边界处施加粘弹性人工边界[8]以防止地震波发生反射。

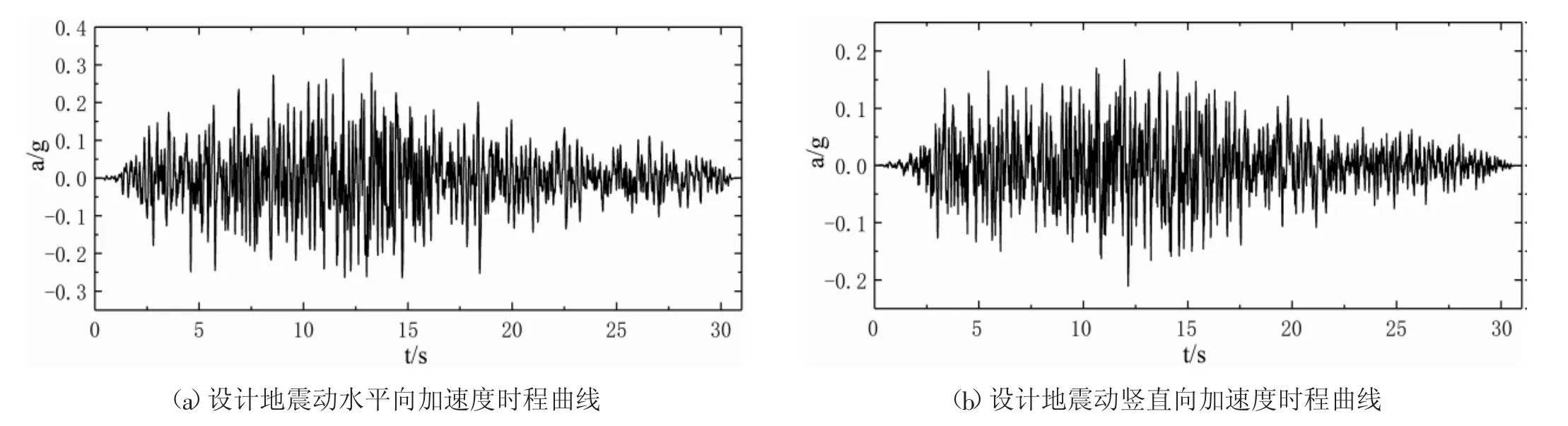
图7 设计地震动时程曲线

3.2 极限抗震能力分析

图8是不同强度地震波作用下坝体损伤区域分布图，可以看出，在0.316g的设计地震动作用后，坝体在下游折坡处附近出现轻微损伤，当0.3651g的校核地震动作用后，下游折坡处附近损伤区域范围扩大，随着地震动强度的不断增加，下游折坡处损伤区域不断向上游面扩展，当地震动强度为0.5g时，下游折坡处损伤区域贯通上游，此时重力坝上部坝体可视为脱离块体，重力坝产生失稳，因此可以判定该重力坝的极限抗震能力为0.5g，相应超载系数为1.58。随着地震强度的不断增加，坝基损伤区域主要沿着软弱夹层不断开展。

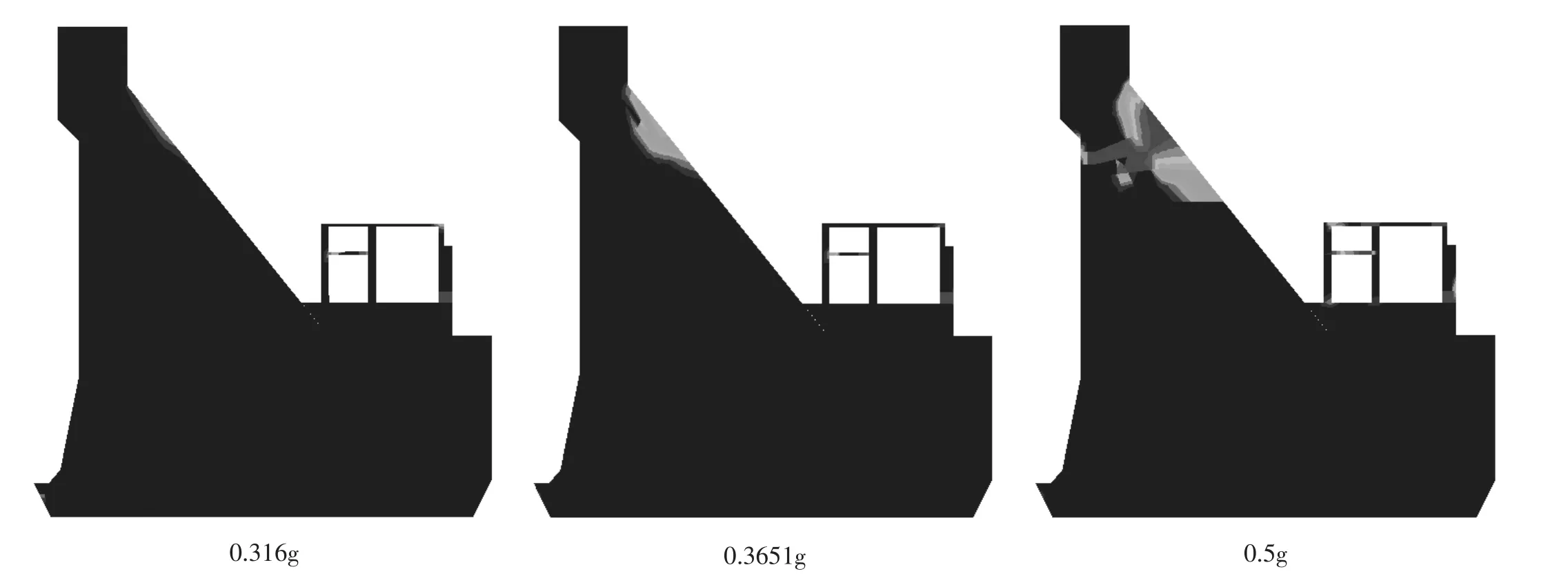
图8 超载地震动作用下的坝体损伤分布图

4 结论

在考虑坝体-坝基整体损伤的基础上，基于时程分析法可以对我国西南某拟建重力坝在不同强度地震下的震损情况进行分析。并以坝体裂缝贯通上下游为失稳判别标准可以对重力坝的极限抗震能力进行评价，且评价结果符合大坝动力特性。

通过计算实例可知，考虑坝体-坝基整体损伤非线性，对设计地震动不断进行超载，当地震动强度为0.5g时，下游折坡处损伤区域贯通上游，此时重力坝上部坝体可视为脱离块体，重力坝产生失稳，因此可以判定该重力坝的极限抗震能力为0.5g。

需要说明的是，本文的基岩损伤模型，在目前阶段建议仅用于前期分析和抗震评价，用于真实设计应同时计算线弹性情况和弹塑性情况，综合分析大坝-坝基的整体安全。