基于非线性微分方程的机械臂运动位置控制方法
宁海成
(咸阳职业技术学院,陕西 咸阳 712000)
0 引言
近年来,随着科学研究的不断发展,机械臂技术也在不断进步,与机械臂相关的生产劳动、医疗卫生、监控装置和农业种植等领域均提出增强机械臂运动位置控制能力的要求[1]。为了紧跟当下社会机械装置更新迭代的速度,满足用户提出的要求,需要对机械臂运动位置的控制性能进行研究。
陈恩志等[2]提出一种采用干扰观测器的水下滑翔蛇形机器人纵倾运动控制方法,但该方法存在机械臂关节节点位置跟踪效果差的问题;龚道雄等[3]提出一种气动肌肉拮抗驱动机器人关节的类人运动控制方法,但该方法存在机械臂运动位置控制能力差的问题;张新良等[4]提出一种双目视觉伺服的4-DOF机械手臂运动控制方法,但该方法也存在机械臂运动位置控制能力差的问题。
为了解决上述方法中存在的问题,提出基于非线性微分方程的机械臂运动位置控制方法。
1 机械臂动力学及非线性微分方程
1.1 机械臂动力学分析
机械臂是由双转动关节连接1个平移关节所组成的多组三连杆[5]结构复合体,每个关节由该关节连接处的液压缸[6]驱动,正常情况下,液压缸伺服阀呈关闭状态,可由人工或系统自动开启。机械臂内部三连杆结构如图1所示。

图1 机械臂内部三连杆结构
图1中标注的三连杆节杆长度和关节角度与机械臂的整体运动息息相关,根据图1中L、Q、r的运动坐标系,可以推导出机械臂内部随机三连杆结构的运动轨迹方程式为
(1)

式(1)主要描述机械臂内部单独三连杆结构的运动轨迹,考虑到机械臂内部多组三连杆结构协同作业,需要对机械臂内部多组三连杆结构的协同运动方式和邻近2组三连杆结构的端点移动方向进行研究。设机械臂内三连杆结构的总数为x,以机械臂内部单个三连杆结构运动轨迹为基础,根据冗余机械臂自由度原理,可以推测机械臂内部多组三连杆结构的运动协作关系和邻近2组三连杆结构的端点移动方向。冗余机械臂自由度原理的表达式为:
(2)
(3)
λ为邻近2组三连杆结构的移动方向;P(w)为多组三连杆结构的的运动协作关系矩阵。
以三连杆结构的运动协作关系矩阵为基础,通过对矩阵进行加权,进而获取机械臂内每个关节的动力权重。矩阵加权[7]的表达式为
(4)
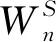
采用梯度投影法量化单位关节的运动权重,使机械臂处于运动饱和状态,有利于机械臂动力学目标函数的建立。梯度投影法的量化表达式为
(5)
μ为梯度投影常数;l为单位关节量化系数;t为探索步长。根据机械臂单位关节的运动权重量化结果,可以推导出机械臂动力学目标函数,机械臂动力学目标函数表达式为
(6)
i为机械臂运动关节参与数量;g为运动关节移动角度的平均值;r为机械臂运动过程中液压机耗能量。
1.2 机械臂的非线性微分方程
在获取机械臂动力学目标函数后,将目标函数进行分解重构,获取机械臂梁单元视角下的非线性微分方程。梁单元视角下,关于机械臂的非线性微分方程将机械臂整体看作多截面、多节点坐标系的杆件状模型,模型的弯曲、拉伸和变形与各截面节点坐标系的弹性位移[8]有关。设截面的2节点坐标系分别为(x0,y0)和(x1,y1),当截面两端的弹性曲率与节点坐标纵向转率的比值超过β时,模型运动参数满足机械臂运动阈值;当截面两端的弹性曲率与节点坐标纵向转率的比值小于β时,模型运动参数不满足机械臂运动阈值,即此时的模型运动无意义。梁单元视角下节点坐标位置的设置如图2所示。

图2 梁单元视角下节点坐标位置的设置
从图2梁单元视角下节点坐标位置的设置可知,节点坐标位置的选择与单位向量转角和转率的取值有关,想要获取单位向量转角和转率的有效取值,需要在模型中加入Lagrange方程[9],获取单位向量转角和转率的几何刚度,并利用梁单位视角下模型动能和势能相结合所获取的非线性耦合参数,将Lagrange方程输出的几何刚度转变成与单位向量对应的刚性位移。刚性位移对于节点坐标的位置选择具有十分重要的意义,在刚性位移的指导下,模型中的各节点坐标整齐排列,且每个单位向量的转角和转率都满足有效取值。Lagrange方程的表达式为
(7)
ω为Lagrange系数;K为单位向量的转角约束变量;X为单位向量的转率约束变量;t为参与获取单位向量转角和转率的模型内节点坐标总数;A为刚性向量。根据Lagrnge方程获取到的单位向量转角和转率的几何刚度表达式为
(8)
σ为几何刚度的常数;S为单位向量转角的空间几何刚度;θ为单位向量转率的位移几何刚度。
非线性耦合参数的表达式为
(9)
f(w)为模型动能系数;f(v)为模型势能系数;(τg)i为非线性耦合参数的输出结果。
将Lagrange方程的输出结果与非线性耦合参数相结合,获取到单位向量对应的刚性位移,单位向量对应的刚性位移获取公式为
(10)
Jx为刚性向量指导节点位置的横坐标;Jy为刚性向量指导节点位置的纵坐标;κ为耦合参数;sin(k0-k1)为邻近节点坐标的刚性距离;tan(k0+k1)为单位向量指导节点的间距;cos(k0+k1)为指导节点坐标的刚性距离;cos(k0-k1)为刚性向量节点的间距。
刚性位移的获取解决了模型内节点坐标的位置排列问题,在已知机械臂动力学目标函数的基础上,利用节点坐标求权矩阵对模型内节点坐标的排列顺序进行赋值,达到重构机械臂动力学目标函数的目的,进而获取机械臂非线性微分方程。坐标求权矩阵的表达式为
(11)
Q为坐标求权系数;G为非线性矩阵赋值率。
最终获取的机械臂的非线性微分方程表达式为
(12)
D为非线性微分方程的常数;Z为机械臂动力学参数。
2 机械臂运动控制模型的建立
CPG神经网络[10]是由多组功能不同的神经元共同偶联而形成的分布式振动网络,该网络结构不仅能激活输入数据的周期性振动信号,还能采集输入数据的运动信息,控制数据的律动节奏,因此CPG神经网络又被称为周期性动力学控制系统。CPG神经网络控制输入数据运动节律的具体操作与第3方神经网络双层级拓扑结构有关,该结构对于运动控制模型的建立具有重要意义。第3方神经网络双层级拓扑结构的数学表达式为
(13)
v为双层级传感神经元的数量;l为机械臂运动控制参数。
利用非线性微分方程获取机械臂动力学参数,并以此为样本数据投入到第3方神经网络双层级拓扑结构中,构建运动控制模型。该模型保留了CPG神经网络的激活与采集功能,同时增加运动状态监视功能和Kuramoto运动稳定功能,使机械臂能够顺利控制运动曲线,矫正运动轨迹偏移所带来的机械臂动力误差。运动控制模型的数学表达式为
(14)
cos(Mi-Mj)为运动状态监视周期;ri,j为运动稳定系数。
运动控制模型矫正机械臂运动轨迹偏移的数学表达式为

(15)
a为机械臂偏移曲线的斜率;b为运动控制模型识别机械臂运动轨迹偏移的概率。
运动控制模型矫正机械臂运动轨迹偏移如图3所示。

图3 运动控制模型矫正机械臂运动轨迹偏移
基于CPG神经网络建立的机械臂运动控制模型能够顺利控制机械臂的运动位置,提高机械臂在生产工作中的效率,加快了机械设备智能化的发展。
3 实验与结果
为了验证基于非线性微分方程的机械臂运动位置控制方法的整体有效性,需要对其进行测试。
选择A、B、C等3种不同型号的机械臂作为实验样本,采用不同方法对3种型号的机械臂分别进行检测,检测内容包括机械臂关节节点控制结果和机械臂运动位置控制结果,根据检测结果推断各方法的运动控制能力。
3.1 机械臂关节节点控制结果
机械臂关节节点的控制建立在节点位置准确跟踪的基础上,采用本文方法、文献[2]方法和文献[3]方法分别跟踪3组不同型号的机械臂关节节点运动角度,并将不同方法针对3种机械臂关节节点运动角度的平均跟踪结果与实际机械臂关节节点运动角度相比较,通过分析不同方法对于机械臂关节节点运动角度的跟踪误差,对比不同方法对机械臂关节节点的控制性能。不同方法对机械臂关节节点运动角度的跟踪结果对比如图4所示。
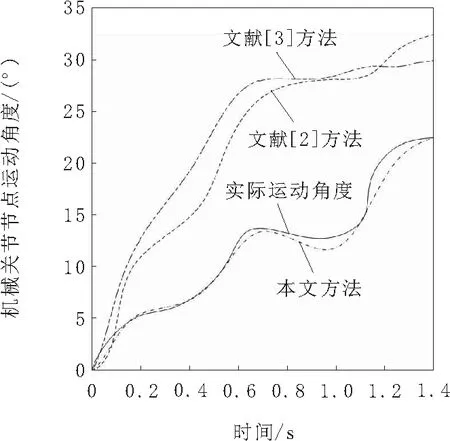
图4 不同方法对机械臂关节节点运动角度的跟踪结果
由图4可知,文献[2]方法和文献[3]方法对3种机械臂关节节点运动角度的平均跟踪结果与实际机械臂关节节点运动角度呈现整体偏离的趋势,本文方法对3种机械臂关节节点运动角度的平均跟踪结果与实际机械臂关节节点运动角度几乎吻合。说明本文方法的节点位置跟踪效果好,即本文方法对机械臂关节节点的控制效果好,这是因为本文方法结合了非线性微分方程,获取到了对机械臂运动位置控制效果显著的机械臂动力学参数,使得平均跟踪结果的误差降至最低,为机械臂关节节点的控制打下良好的基础。
3.2 机械臂运动位置控制结果
为了进一步验证不同方法下机械臂的运动位置控制性能,采用本文方法、文献[3]方法和文献[4]方法分别对3种型号的机械臂运动位置进行控制,对比3种型号机械臂的目标运动位置与不同方法控制下的运动位置,分析不同方法对机械臂运动位置的控制结果,以此展现不同方法对机械臂运动位置控制性能。机械臂的目标运动位置与不同方法控制下3种型号机械臂的运动位置对比如图5~图7所示。

图5 机械臂的目标运动位置与本文方法控制下的

图6 机械臂的目标运动位置与文献[3]方法控制下的

图7 机械臂的目标运动位置与文献[4]方法控制下的
由图5可知,本文方法控制下3种型号的机械臂运动位置与目标运动位置几乎一致,完美贴合目标运动曲线,说明本文方法对于机械臂的运动位置控制能力强,控制系统出现误差导致运动轨迹偏移的几率低。由图6和图7可知,文献[3]方法和文献[4]方法控制下3种型号的机械臂运动位置与目标运动位置并不一致,运动位置控制能力差。经上述对比可知,本文方法在不同型号机械臂中的都能表现良好的位置控制能力。
4 结束语
机械臂不论是在生产流水线上,还是在科学研究领域都起到相当重要的作用,因此对机械臂的要求也越来越高。传统的机械臂在工作期间常表现出运动位置不受控的问题,为了提高机械臂的运动位置控制能力,提出基于非线性微分方程的机械臂运动位置控制方法。如何保证机械臂提升运动位置控制能力的同时,加快机械臂的运动速度,提升生产劳动或科学研究的效率,是研究人员下一步工作的重点。

