大跨度高大平房仓粮堆热湿传递过程的数值模拟及试验

袁越锦， 戴 航， 石天玉， 李倩倩

(1.陕西科技大学 机电工程学院, 陕西 西安 710021; 2.国家粮食和物资储备局科学研究院, 北京 100037)

0 引言

储粮平房仓因其容量大、进出仓便利、造价低的特点被广泛应用.目前国家储备粮库中所建的粮仓仓型80%以上为平房仓[1].而大跨度高大平房仓作为平房仓的一种，通过在跨度方向上的中间位置增加两组对称式进风风道，将粮面上的冷空气引入粮堆，其优点在于提供了特殊大跨度仓型的横向通风系统的技术实施方案[2].大跨度高大平房仓装粮线高、跨度大、通风系统双侧分布的工艺特点和土地的高利用率为其提供了广阔的应用和发展空间.

粮食在仓储过程中影响其安全的主要生态变化是粮堆的霉变、发热和仓内害虫的生命活动，而影响生态变化的重要因素是粮堆及仓储环境的温度和湿度[3].Marcelino C R等[4]提出，冷却干燥通风是一种通过把粮食温度和水分降低到安全阈值，从而降低储粮变质率的有效方法.

横向通风作为常用的粮仓降温保水通风方式，既避免了径向通风的地上笼铺设造成的粮食进出仓不便，实现了粮食进出仓机械化，也大大加强了粮食的热湿对流.杨冬平等[5]通过实验验证了横向通风技术在大跨度稻谷平房仓的应用上具有良好的通风降温效果.G.R.Thorpe[6]建立了一维数值模型，以物性参数对横向通风过程的影响进行了研究，分析了粮食储藏中传热传质过程对通风效果的影响.陈桂香等[7]、王远成等[8]、王珂等[9]通过建立粮堆干燥通风过程的热湿耦合模型并与实验值进行对比，说明数值模拟可应用于粮堆横向通风过程研究并指导粮仓通风系统优化.俞晓静等[10,11]在粮仓的宽度方向上进行了不同相对湿度差条件下的横向通风数值模拟研究，分析了降温保水的最佳送风条件.但横向通风在大跨度平房仓的应用中仍存在通风路径长，粮堆温度在跨度方向上分层大等工艺问题.且目前尚未有基于数值模拟对54 m大跨度高大平房仓进行热湿传递的应用研究.

本研究以黑龙江省绥化市秦家粮库58号高大平房仓的降温通风实验为研究对象，采用数值模拟的方法对大跨度高大平房仓的降温保水横向通风工艺进行研究，分析了中间风道进风、双侧负压吸出式通风工艺的降温保水效果，探究了通风过程中粮堆的温度场变化、54 m大跨度平房仓在不同温差和不同通风风速下实现降温保水的所需时间.研究结果可以为实仓通风操作提供技术依据，保障粮食的安全储存.

1 试验部分

1.1 粮仓结构

实验仓长度为54 m，跨度为24 m，高11 m，粮堆高度8.2 m.该粮仓采用横向通风系统，两侧布置主风道和竖向支风道，两侧各设2个600 mm直径的出风口.4个出风口处各设置1个负压风机.仓房横向27米处有支撑柱，支撑柱两侧各设10个竖向支风道，支风道上端开口，为进风口.粮堆表面中心支风道进风口以外的区域均覆盖塑料薄膜.大跨度高大平房仓横向通风工艺如图1所示.粮堆中间支风道(通风笼)上端为进风口，粮堆两侧支风道下部水平段竖向外侧为出风口.通风过程中，气流由进风口进入中间支风道，通过中间支风道壁面并穿过粮堆后进入粮堆两侧支风道，并由设置于粮堆两侧支风道下端的负压风机吸出.

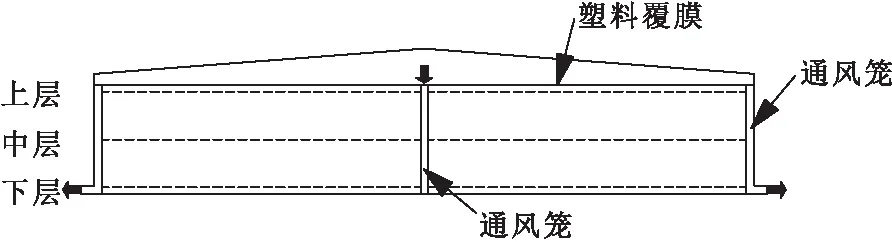
图1 大跨度高大平房仓横向通风工艺示意图

1.2 试验粮种及方法

本试验采用试验粮种为黑龙江绥化粳稻，水分含量为14.5%，数量为6 721吨.实验环境为冬季气候，气温-10 ℃～-21 ℃.具体实验过程如下：从11月17日开始，11月27日结束，总共通风240 h.打开仓内通风窗，同时开启仓底南北两侧的风机进行通风.实验采用4台7.5 kW风机，系统总风量为38 740.44 m3/h，南北两侧4个出风口各设置一台.

目标粮仓装备了数字式粮堆温湿度检测系统，通风过程中测量点共198个，横向6行、纵向11列，高度方向分3层布局，检测精度为±0.2 ℃，上层检测点距离粮面0.5 m，中层检测点位于粮堆中心高度，下层检测点距离仓底0.5 m.符合LS/T1203-2002的规范要求.粮堆温度和水分均通过数字式温湿度检测系统定时测定.

1.3 试验结果

通风前粮堆相对湿度情况如表1所示，通风后粮堆相对湿度情况如表2所示.上层水分通风后比通风前减少0.3%，中层水分通风后比通风前减少0.3%，下层水分通风后比通风前减少0.2%，整个粮堆的水分通风前后水分减少0.3%，粮堆水分保持效果好.

表1 通风前粮堆相对湿度情况

表2 通风后粮堆相对湿度情况

图2为通风0 h至240 h各竖向截面平均温度变化.可看出各截面粮食平均温度均呈下降趋势，且最终均下降至-7 ℃～-15 ℃.

图2 竖向截面平均温度变化

本次实验风量固定，粮堆内垂直方向上的空气流速由粮面至仓底逐渐降低，水平方向上的空气流速由中间支风道向两端逐渐下降，使得粮堆内温度分布不均.采用双侧负压吸出全覆膜式的降温保水横向通风工艺，有效解决了仓房跨度大导致的降温不均.实验结果表明，本次54米跨度稻谷仓横向保水通风降温保水效果较好.

2 高大平房仓粮堆热湿耦合模型的建立

2.1 物理模型

横向通风时，由于粮仓长度方向的温度和水分的梯度相对于粮仓高度和跨度方向上较小，分析粮仓内部温度和水分分布规律时，可以将其简化为二维问题进行研究[6].以实验仓为研究对象，由于在横向通风过程中粮面为覆膜状态，且进风口只有中间的支风道，故可以将覆膜视为绝热边界，对粮面覆膜及以下的区域进行建模.构建了如图3所示的物理模型.粮仓跨度为54 m，粮面覆膜高度为8.2 m.粮仓中间和两侧均设置有直径为600 mm的通风管道，气流由中间通风管道上进口进入，并由仓底两侧的负压风机经出风口吸出.本模型共划分网格134 634个.

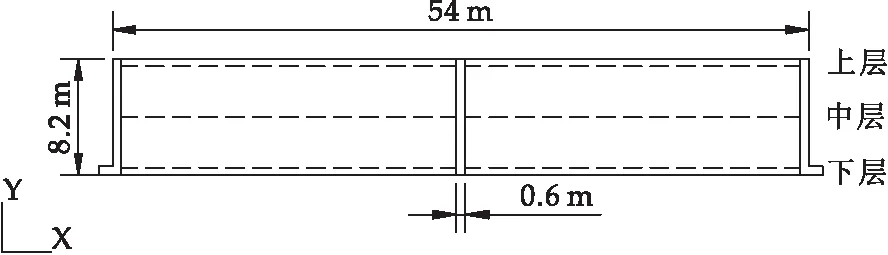
图3 物理模型

2.2 数学模型

假设粮堆为密度均匀的多孔介质，满足局部热平衡原理[12].由于粮堆内部通风阻力较大，气流在粮粒间隙中的流动速度很慢，可将气流在粮堆内的流动看作层流.粮堆通风热湿耦合的控制方程如下.

2.2.1 连续性方程

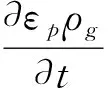
(1)

式(1)中：εp为孔隙率；ρg为空气密度，kg/m3；u为湿空气的表观速度，m/s；为哈密顿算子.

2.2.2 动量方程

粮堆内部流动空气的动量变化符合动量守恒原理.

(2)

(3)

式(2)、(3)中：p为压力，Pa；I为内能，J/kg；K为黏性力，N/m2；μ为动力粘度，Pa·s；κ为渗透率，m2；β为压缩系数，1/Pa.

2.2.3 水分迁移方程

对于粮堆内的水分迁移可由局部热平衡理论推导得出.

(4)

式(4)中：w(φw)为蓄水量函数；t为时间，s；ug为气相速度场，m/s；ωv为蒸汽质量分数；gw为水汽通量，kg/(m3·s)；ul为液相速度场，m/s；ρl为液相密度，kg/m3；gIc为毛细管液体通量密度，kg/(m2·s)；G为水汽源，kg/(m3·s).

w(φw)=εp(ρlsl+ρgωv(1-sl))

(5)

式(5)中：sl为液态水饱和度.

gw=-ρgDeffωv

(6)

式(6)中：Deff为有效扩散系数，m2/s

(7)

式(7)中：φw为相对湿度；csat为饱和浓度，mol/m3.

(8)

式(8)中：κrl为液态水相对渗透率；μl为液态水的动力黏度，Pa·s；pA为绝对压力，Pa；g为重力加速度.

2.2.4 能量方程

对于粮堆内的能量方程可由热力学第一定律推导得出，

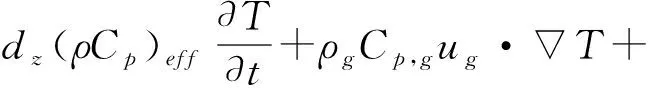
(9)

式(9)中：(ρCp)eff为有效体积热容，J/(m3·K)；T为温度，K；ρgCp,gug为湿空气的传热系数，W/(m2·K)；ρlCp,lul为液相水传递的传热系数，W/(m2·K)；q为单位面积热通量W/m2；Q为热源，W/m3；q0为向内热通量，W/m2；Qevap为潜热源，W/m3；dz为厚度，m.

(10)

式(10)中：keff为有效导热系数，W/(m·K).

(ρCp)eff=θsρsCp,s+εp((1-sl)ρgCp,g+slρlCp,l)

(11)

式(11)中：θsρsCp,s为多孔基体有效体积热容，J/(m3·K)；Cp,g为气相热容，J/(kg·K)；Cp,l为液相热容，J/(kg·K).

keff=θsks+εp((1-sl)kg+slk1)

(12)

式(12)中：θs为多孔基体的体积分数；ks为多孔基体导热率，W/(m·K)；kg为气相导热率，W/(m·K)；kl为液态水的导热率，W/(m·K).

(13)

Qevap=Gevap·Lv

(14)

式(13)、(14)中：Ωv为蒸汽质量分数；Gevap为相变系数，kg/(m3·s)；Lv为相变潜热，J/kg；Mv为水蒸气摩尔质量，mol/m3；ux为湿空气在x方向上的表观速度，m/s；uy为湿空气在y方向上的表观速度，m/s.

2.3 边界和初始条件设置

在本试验中，边界和初始条件的设置分别如表3和表4所示.

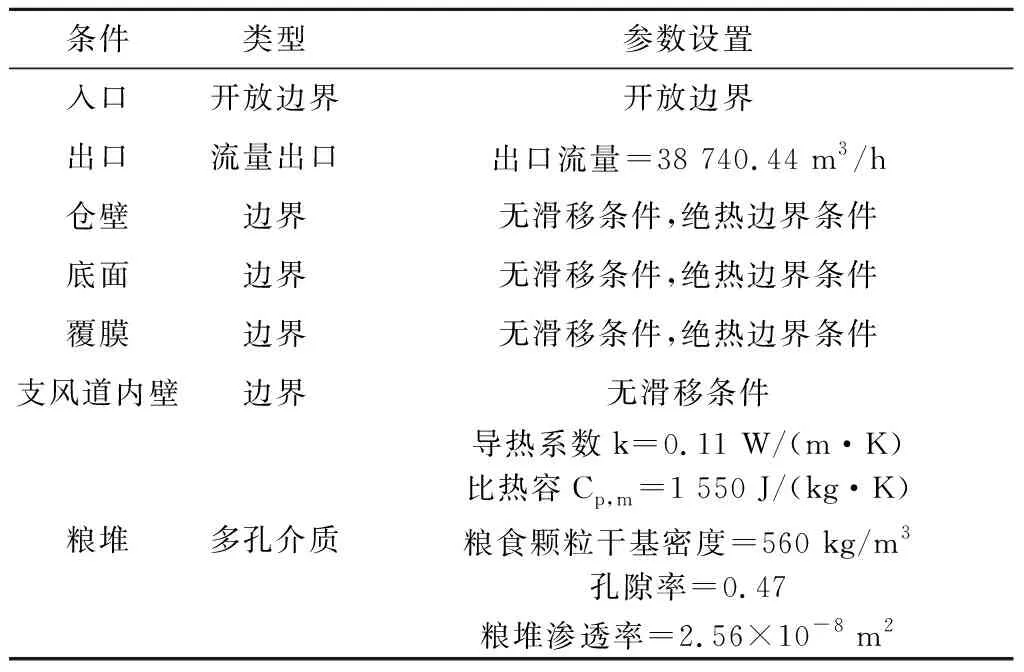
表3 边界条件设置

表4 初始条件设置

3 结果验证与分析

3.1 数值模拟的准确性验证

图4为实仓实验和模拟实验的平均温度结果对比，图4中粮堆实测平均温度可由图2得到.可以看出，实仓实验的平均温度值与模拟实验的平均温度值的变化趋势基本相符，表明该数值模拟模型可以较准确的预测温度的变化.实仓实验的温度值略小于模拟实验的温度值，原因是模拟实验中将覆膜视为完全绝热的边界，实仓实验中粮堆表面覆膜与支风道、覆膜与粮仓壁面之间无法完全封闭，存在一定的能量损失.

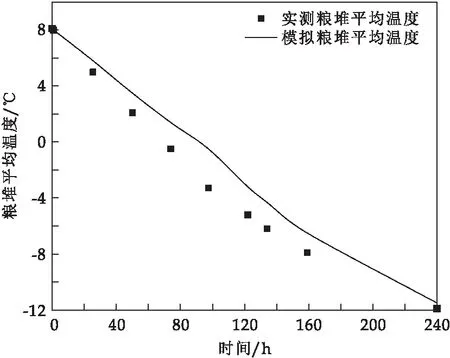
图4 实仓实验和模拟实验的平均温度结果对比

粮堆的上层位置取距粮堆表面0.5 m处二维水平截线，中层位置取粮堆中心高度处二维水平截线，下层位置取距仓底0.5 m处二维水平截线，并对各层水分取平均值.

图5为开始通风时粮堆初始水分和通风240 h时后粮堆水分比较.可以看出，实仓实验中粮堆各层水分下降幅度0.2%～0.3%，数值模拟实验中粮堆各层水分下降幅度为0.1%～0.2%，仅相差0.1%，与实验基本吻合.数值模拟的整个粮堆的平均水分由通风前的14.5%下降至14.3%，与实仓实验值14.2%基本吻合，仅相差0.1%.进一步证明该数值模拟模型具有较高的精度.

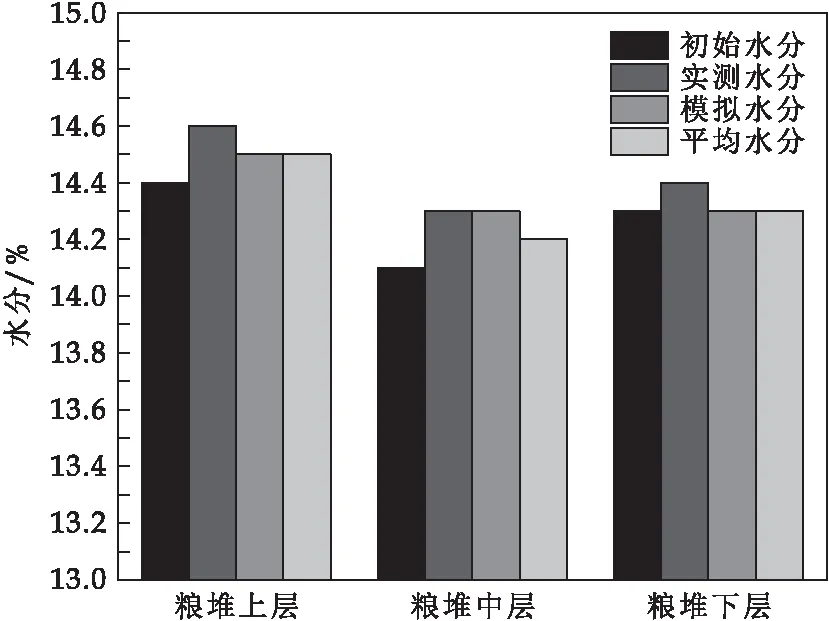
图5 粮堆初始水分和通风240 h时粮堆平均水分比较

3.2 通风过程的流场

通风时粮堆内的流场如图6所示，空气流动的动能由仓房两端的负压风机提供.由于粮面有覆膜，空气由平房仓中间支风道的上端开口进入并充满整个中间支风道后，沿水平方向穿过整个粮堆，经两侧的支风道流入底部的主风道，再由主风道出口的负压风机吸出.进口和出口处的空气流速较大，达1.26 m/s，表观风速均为0.026 1 m/s.中间支风道的空气通过支风道上的通孔通向两侧的粮堆内，支风道内的空气流速由上至下不断下降，且由于在支风道底部空气会产生回旋，使支风道下部空气流速下降较上部空气流速下降更快.

图6 通风时粮堆内部空气速度场

3.3 数值模拟通风240 h时的温度场和水分场

本次模拟目的为分析粮堆内部温湿度变化，故在对模型计算结果的后处理中进行了定义选择，只显示粮堆部分的计算结果.

图7为通风240 h时粮堆的水分场，图8为通风240 h时粮堆的温度场.由图7可以看出，通风结束后粮堆水分分布均一.主要原因是本模型依据实际粮堆初始水分分布情况(上中下三层水分相差最大为0.2%)进行设置，可近似认为初始粮堆水分分布均匀，同时结合图6，由于粮堆内部通风阻力较大，气流在粮粒间隙中的流动速度很慢，可将气流在粮堆内的流动看作层流，速度场分布基本均匀.由图8可以看出，通风结束后温度场除贴近两侧通风管道出高于-7.8 ℃其余部分均低于-7.8 ℃，模型整体通风均匀性较好，降温保水效果明显.

图7 通风240 h时粮堆水分场

图8 通风240 h时粮堆温度场

3.4 数值模拟通风过程中的温度变化结果分析

图9为通风172 h粮堆内部的温度场，图10为通风200 h粮堆内部温度场.由图10可看出，粮仓跨度15 m和40 m处粮堆的中上部均出现了局部温度较低的区域，其原因是中间支风道内空气的速度由上至下逐渐降低，导致粮堆底部空气流速低于中部和上部，使得粮堆中上部温度下降较下部更快.结合图9可看出，当冷锋面沿气流方向2/3处后，剩余部分温度下降缓慢，对于靠近出风口粮堆部分温度下降尤为缓慢.原因是粮堆为吸湿性多孔介质，通风时会产生解吸湿过程，吸收粮粒间气流的热量.由于热量在传递过程存在延迟和衰减现象，在与风口距离不同的粮层间存在一定的温度梯度，离进风口较远的粮层温度变化较为缓慢[9].

图9 通风172 h时粮堆温度场

图10 通风200 h时粮堆温度场

3.5 数值模拟不同进风温度和出风速度对粮堆降温时间的影响

根据LS/T 1202-2002《储粮机械通风规程》中对通风温度的规定[13].开始通风时，粮堆平均温度和进风温度差值应大于等于8 ℃.这是根据节能降耗的经济性原则提出的.当温差大于8 ℃的时候，温差增大对于减少降温时间没有显著意义；温差在0 ℃～8 ℃内，温差减小会导致降温时间急剧增加，在温差接近0 ℃的时候，降温时间趋于无穷大[14].故模拟了粮堆初始平均温度和进风温度差值大于等于8 ℃时，不同进风温度和出风速度对粮堆降温时间的影响.

图11是不同进风温度下的表观速度和所需降温时间变化趋势，使用不同进风温度的气流对粮仓内的粮堆进行降温，随着进风温度由-17 ℃逐步提升至-4 ℃，表观风速呈下降趋势，粮堆平均温度从8.2 ℃下降至0 ℃所需的时间由37 h增长至108 h，粮堆平均温度从8.2 ℃下降至0 ℃所需的时间呈增长趋势.主要原因是随着进风温度的上升，进风与粮堆初始温差逐渐减小，传热效率降低，同时，进风和粮堆初始温差的减小也导致表观风速的降低，减少了粮堆和粮堆内气流的换热，降低了降温速率，延长了降温时间.

图11 不同进风温度下的表观速度和所需降温时间变化趋势图

图12是不同出口风速下的表观速度和所需降温时间变化趋势图，使用不同出口风速的气流对粮仓内的粮堆进行降温，随着出口风速由0.24 m/s不断提升至0.31 m/s，表观风速呈下降趋势，粮堆平均温度从8.2 ℃下降至-11 ℃所需的时间由228 h缩短至176 h，粮堆由8.2 ℃降至-11 ℃所需时间呈减少趋势.主要原因是随着出口风速的加快，加快了粮堆和粮堆内气流的换热，提高了降温速率，缩短了降温时间.

结合图11、图12，交点处的出口风速和进风温度为最经济的通风工艺.进风温度为-9 ℃时计算得表观风速0.019 3 m/s，可采用4台3 kW风机进行通风作业，粮堆平均降温至0 ℃所需电量为696 kW·h.出口速度为0.28 m/s时计算得表观风速0.022 m/s，可采用4台7.5 kW风机进行通风作业，粮堆平均温度降至-11 ℃所需电量为6 090 kW·h.

图12 不同出口风速下的表观速度和所需降温时间变化趋势图

4 结论

本文以黑龙江绥化秦家粮库58号平房仓为研究对象，对双侧负压吸出全覆膜式的降温保水横向通风工艺进行了数值模拟研究，对比分析了实验和数值模拟的数据，得出以下结论：

(1)采用双侧负压吸出全覆膜式的降温保水横向通风工艺可以实现粮堆的降温保水通风，解决了仓型跨度过大，导致的粮堆降温不均的问题，且保证了通风过程中粮堆水分基本不变.

(2)粮堆初始平均温度相同时，进风温度由-17 ℃提升至-4 ℃，通风时间由37 h延长至108 h.出口速度由0.24 m/s提升至0.31 m/s时，通风时间由228 h缩短至176 h.

(3)利用数值模拟软件进行建模，可对实验过程进行模拟，直观地查看通风过程中粮堆内的流速、温度和水分的变化情况.为实仓降温通风保水操作提供参考，保障粮食的安全储存.

(4)改变进风温度或出口风速会对所需的通风时间产生影响，建立进风温度与表观风速、出口风速与表观风速的关系可得到经济的通风时间，并为选择合理功率的风机提供依据.