深层高产碳酸盐岩油藏试井解释模型及其应用

金子一, 贾 品, 程林松, 张向阳, 孙兆乐, 胡江鹏

(中国石油大学(北京) 石油工程学院, 北京 102249)

0 引言

深层高产碳酸盐岩油藏普遍具有埋藏深、压力高、基质致密、裂缝发育、构造复杂等特点.不同油藏，甚至同一油藏不同构造位置的储层特征都存在差异[1].其储集空间包括形状多样、大小悬殊、分布不均的孔隙、裂缝等，同时由于较高的产量带来的近井地带高速非达西流动，流体在储层中的渗流规律复杂，常规试井模型的适用性欠佳，给储层参数反演带来了极大的不便[2].

早在20世纪60年代，苏联的Barenblatt等[3]和美国的Warren等[4]就提出了双重孔隙介质的概念，促进了双重介质渗流规律的研究.目前，国内外学者对双重孔隙介质油藏试井解释开展了大量研究工作.早期，葛家理等[5]研究了圆柱形裂隙油藏中心一口井定压生产时的渗流特征，求得了数学模型在各边界条件下的解析解.赵子刚等[6]针对双重介质油藏无限大地层和圆形封闭地层压力分布的数学模型，给出了具有井储和表皮井的压力响应样板曲线图.随后，贾永禄[7]研究了考虑表皮和井储的圆形封闭双重介质地层中心一口井生产的有效井径试井数学模型，采用Laplace变化求得拉式空间的解并通过Stehfest数值反演将拉式空间解转换到真实空间.贾永禄等[8]针对井筒周围污染及地层的非均质情况，建立了双重介质复合油藏试井解释数学模型并给出该问题的现代试井样板曲线.此外，王建忠等[9]建立了考虑裂缝渗透率变化模型和变渗透率模量的双重孔隙油藏压力动态模型，由于模型复杂只能得到数值解.陈引弟[10]建立并求解了考虑井储、表皮及应力敏感的双重介质油藏试井数学模型，绘制了三类边界条件下的无因次井底压力及压力导数曲线，最后将Saphir得到的数值解与零阶摄动解进行对比.傅礼兵等[11]基于Izbash指数式方程建立井筒附近存在高速非达西渗流的数学模型，利用Boltzmann变换得到模型的解析解，同时讨论了渗透率、孔隙度和流体黏度等参数对非达西渗流的影响.此外，国内专家学者也对深层高产双重孔隙介质油藏试井解释做了大量研究[12-17].

目前，对于深层高产碳酸盐岩油藏试井模型的研究主要存在2点缺陷：一是,多以摄动变换考虑应力敏感.摄动变化本身是忽略了二阶量，模拟精度下降，并且通常适用于一般强度的应力敏感，对于高强度应力敏感不适用；二是,针对高产量带来的近井地带高渗流速度导致的高速非达西流动，一般方法常采用非线性处理，计算速度较慢，拟合效率偏低.

为弥补已有研究的不足，本文将在前人的基础上，针对深层高产碳酸盐岩油藏两大特征，分别引入拟压力和表皮系数，考虑大埋藏深度带来的强应力敏感问题以及高产量、高渗流速度造成的高速非达西流动，建立裂缝孔隙型双重介质试井解释模型，分析压力曲线特征及敏感性参数的影响，并通过T油田某实例井生产动态数据反演储层关键参数，以验证解析解模型结果.

1 物理模型

考虑非均质矩形封闭油藏中，一口直井(如图1所示，k为地层渗透率，x、y、h分别为储层长度、宽度和高度).储层为深层高产碳酸盐岩裂缝孔隙型双重介质，通过井筒的流动是经过裂缝的，基岩作为源，且介质之间发生拟稳态窜流.

模型的基本假设条件：

(1)地层水平等厚，地层中心一口井，井以定产量生产；

(2)产层厚度全部打开，流体径向流入井内；

(3)地层流体和岩石微可压缩，流体为单相，且压缩系数为常数；

(4)地层流体在近井地带为高速非达西渗流，其他区域满足线性达西定律；

(5)考虑储层裂缝系统的强应力敏感作用；

(6)考虑井筒储存和表皮的影响，忽略重力和毛管力的影响.

图1 深层高产碳酸盐岩油藏裂缝孔隙型双重介质物理模型示意图

2 数学模型

深层高产碳酸盐岩油藏的模型构建过程中主要考虑裂缝系统的强应力敏感和高速非达西流动.储层应力敏感主要指上覆地层有效应力相对变化引起储集空间(孔隙、裂缝及溶洞)发生形变，导致储层物性参数变化的现象，裂缝型碳酸盐岩储层应力敏感尤为突出[18].油气开采过程，储层应力敏感可能引起储层渗透率损失加剧，渗流能力受到制约，产量随之降低，认识和量化裂缝型储层渗透率应力敏感具有重要意义.对于应力敏感问题，应力敏感系数表示有效应力每改变单位压力时，单位渗透率的改变值，其表征了储层渗透率随应力变化的敏感程度，该值越大代表储层敏感性越强[19].引入应力敏感系数γf和渗透率模量，则裂缝渗透率可表示为：

(1)

kf=kfie-γf(pi-pf)

(2)

式(1)～(2)中：k为岩石初始渗透率，D；∂k为渗透率改变值，D；∂p为有效应力改变值，atm；γf为应力敏感系数，atm-1；kfi为裂缝初始渗透率，D；kf为裂缝当前渗透率，D；pi为原始地层压力，atm；pf为裂缝渗透率，atm.

为使渗流方程线性化，定义基质系统拟压力为ψm，裂缝系统拟压力ψf.由于只考虑裂缝系统的应力敏感，故基质系统拟压力ψm等同于Pm，而裂缝系统拟压力ψf为：

(3)

储层中的油气渗流通常遵循达西定律，但在深层高产碳酸盐岩油藏中，由于渗流速度大，特别是在井底附近，流体将呈非达西高速流动[20].室内试验和开发实践表明：当流体的渗流速度较大时(雷诺数Re>0.1)，呈现出高速非达西渗流，达西定律无法准确地描述其渗流规律[21].对于高速非达西问题，引入与流量相关的表皮系数sd表示，则其所引起的附加压力降为：

(4)

(5)

对于裂缝型双重介质单相流体渗流数学模型的建立，需综合以下方程[22]：

根据质量守恒原理，建立无限大地层裂缝型双重介质油藏流体不稳定渗流的基本微分方程如下所示：

裂缝系统：

(6)

基质系统：

(7)

初始条件、内边界条件：

ψf|t=0=ψm|t=0=0

(8)

(9)

外边界条件考虑无限大外边界：

(10)

引入有效井径，定义量纲压力、量纲距离、量纲时间、量纲存储系数及其他参数为：

式(6)～(10)中：rD—无因次井径；rw—井筒半径，cm；r—地层某点离井筒中心的距离，cm；tD—无因次时间；ψD—无因次拟压力；ψi—原始地层拟压力，atm；ψ—地层某点的压力，atm；q—地面产量，cm3/s；B—体积系数，无因次；t—时间，s；s—表皮系数，无因次；φ—孔隙度，%；Ct—综合压缩系数，atm-1；h—储层厚度，cm；CD—无因次存储系数；C—存储系数，cm3/atm；λ—窜流系数；αm—形状因子，cm-2；km—基质系统渗透率，μm2；kf—裂缝系统渗透率，μm2.

得到以下无因次数学模型：

(11)

(12)

初始条件、内边界条件：

ψfD|tD=0=ψmD|tD=0=0

(13)

(14)

考虑无限大外边界：

(15)

3 模型求解

对以上方程作基于tD/CD的Laplace变换，并利用初始条件，整理可以得到:

(16)

(17)

对以上方程在Laplace空间上进行求解，对公式(17)求解得：

(18)

将公式(18)带入公式(16)化简得：

(19)

由上式整理可得：

(20)

可令：

(21)

则有：

(22)

内边界条件：

(23)

对于无穷大外边界，则模型的解为：

(24)

(25)

式(25)中：u为拉普拉斯变量；K0、K1分别为零阶、一阶第二类贝塞尔函数.

在油气藏的实际生产中，一口生产井的井底压力除受地层流体及渗流环境的影响外，还要受到井筒储集效应和表皮效应等因素的影响.Van Everdingen A F[23]指出，在Laplace空间中将无因次井底压力PwD带入以下等式可以考虑井筒储集效应和表皮系数的影响，同时若生产井以定井底流压生产，则可以得到考虑应力敏感性和高速非达西的无量纲井底拟压力为：

(26)

4 曲线分析

4.1 流动阶段划分

对上述三类外边界条件下的Laplace空间的解析解，利用Stehfest数值算法进行数值反演，可以得到实空间的解Pw，从而利用数值解编程绘制无因次试井样版曲线.

图2 裂缝孔隙型储层无量纲井底压力及压力导数双对数曲线

由图2可知，深层高产碳酸盐岩油藏裂缝孔隙型储层压力响应曲线有6个阶段：

第Ⅰ段是早期井筒储集效应.两条曲线为直线段，且斜率为1.井筒储集效应的大小用井筒储集系数C来表示，单位为m3/MPa，反映了井筒流体每增加或减小单位压力引起的井筒流体受弹性压缩性影响的体积变化量.

第II段为表皮效应阶段.当开井生产一段时间后，井底压力下降，地层流体开始流入井底后，地层压力下降，压力波开始在地层中扩散.地层压力降落幅度大小首先受表皮系数的影响，储层污染越严重，表皮系数越大，附加压力损失也就越大.根据无因次压力的定义，无因次压力与地层压力降线性相关，因此表皮系数越大，无因次试井样版曲线位置越高，压力导数曲线“驼峰”效应越明显，对应现场关井前的产量越大，井底污染越严重.

第III段为地层裂缝系统径向流阶段.因天然裂缝渗透率远大于基质渗透率，天然裂缝的流体优先流入井筒，天然裂缝网络中流体径向流入井筒.在此阶段，基质流体并未流动，因此基质系统压力(Pm)等于原始地层压力(Pi)，天然裂缝系统压力(Pf)大于井底流压(Pwf)，但小于基质系统压力，有压力关系式Pi=Pm>Pf>Pwf.试井样版曲线上的压力导数曲线呈一条水平线是地层裂缝系统径向流的特征响应，反映压力波以圆形向外传播.

第IV段为地层基质系统向天然裂缝系统窜流阶段.在天然裂缝系统与基质系统压力差的作用下，基质流体向天然裂缝系统中窜流，再经天然裂缝系统流入井筒.在此阶段，基质系统流体流动而发生能量衰竭，基质系统压力小于原始地层压力(Pi)，有压力关系式Pi>Pm>Pf>Pwf.试井样版曲线上的压力导数曲线呈“V”形状的凹子，是基质系统流体向天然裂缝系统窜流的特征响应.

第V段为地层基质系统和天然裂缝系统整体径向流阶段.基质流体向天然裂缝系统窜流结束，基质系统压力和天然裂缝系统压力同步衰竭，基质和天然裂缝系统中流体整体径向流入井筒.在此阶段，有压力关系式Pi>Pm=Pf>Pwf.试井样版曲线上的压力导数曲线呈一条水平线，是基质系统和天然裂缝系统整体径向流的特征响应.

第VI段为外边界响应阶段.压力波传到边界后，基质和天然裂缝系统仍整体径向流入井筒.若为恒压外边界，边界处有恒定的压力Pe，则渗流最终将达到稳定流动状态.试井样版曲线上的压力导数曲线急剧下掉，是定压外边界特性响应.若为封闭外边界，则渗流最终将达到拟稳定流动状态，无流体渗流穿越边界，边界处压力对距离坐标的法向导数为0，地层中基质和裂缝系统压力同步衰竭，且任意一点的压力随时间的变化率为一常数.试井样版曲线上的压力和压力导数曲线急剧上翘，最终交会成一条单位斜率的直线，是封闭外边界特性响应.

4.2 影响因素分析

深层高产碳酸盐岩油藏裂缝孔隙型储层压力响应特征主要考虑4个影响因素，分别为：储容比、窜流系数、应力敏感及表皮系数.

4.2.1 储容比ω与窜流系数λ

裂缝储容比ω代表裂缝系统的弹性储容能力占总系统的弹性储容能力的百分数[21].ω越小，则天然裂缝系统的储集能力越弱，基质系统的储集能力越强，基质和裂缝系统的储集能力差异性就越大，反映基质向裂缝窜流的压力导数曲线的凹子就越深.由图3可知，裂缝储容比ω的大小决定窜流段压力导数曲线下凹的深度和宽度，裂缝越发育，凹子越窄越浅.

图3 储容比ω对曲线形态的影响

根据基质系统向裂缝系统窜流系数的定义[21]，基质和裂缝渗透率之比越小，即基质和裂缝系统渗透率差异越大，窜流系数越小.λ决定窜流段压力导数曲线凹子出现时间的早晚.基质系统向裂缝系统窜流的时间越早，基质系统流体流动而发生能量衰竭越早，则基质系统压力降低到小于原始地层压力的时间越短，地层裂缝系统径向流持续时间就越短.由图4可知，窜流系数λ影响凹子出现时间早晚，裂缝基质差异越大，窜流时间越晚，凹子越往右移.

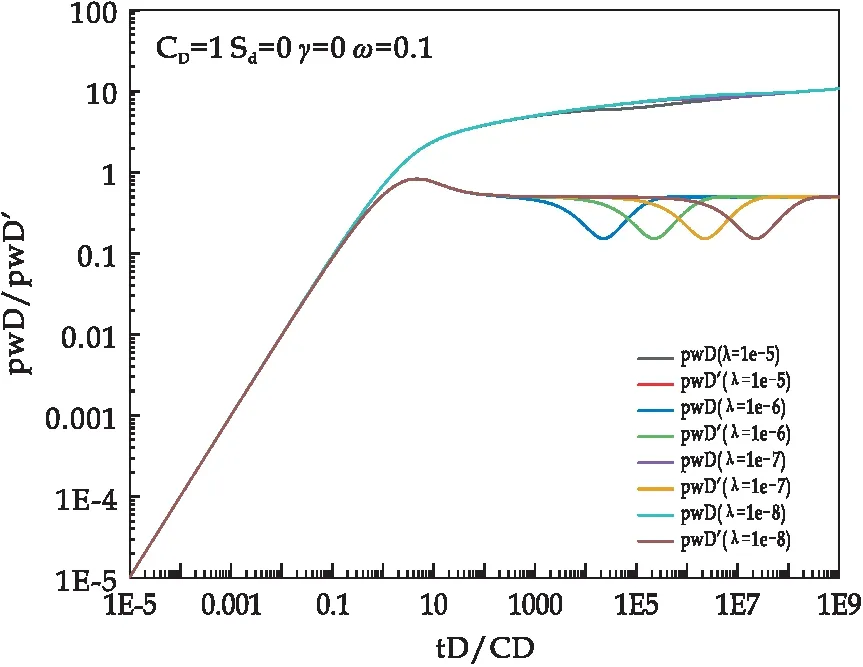
图4 窜流系数λ对曲线形态的影响

4.2.2 应力敏感γ与表皮系数Sd

由图5可知，考虑应力敏感对无量纲压力及压力导数双对数曲线有较大影响.在第Ⅰ阶段，应力敏感影响可以忽略；但进入第Ⅱ阶段后，无量纲压力及压力导数曲线均随应力敏感系数增加而有所抬升，且随时间增加，曲线上升幅度越大；其中，在第Ⅲ阶段和第Ⅵ阶段中，随应力敏感系数增加，无量纲压力导数曲线水平段值以0.5为起点逐渐增大，起点处对应应力敏感系数为0，此时无应力敏感效应.上述变化规律的原因在于，井筒储集阶段中，井筒供液来源主要为井筒存储，储层的渗流能力对该阶段影响不大；而井筒储集阶段结束后，储层各储集空间成为井筒的供液来源，应力敏感效应制约了储层渗流能力，应力敏感效应越强，对应生产现场驱动流体流动所需压力越高.

图5 应力敏感γ对曲线形态的影响

由图6可知，由于在近井地带出现高速非达西渗流，流体流动不再满足达西定律.近井地带的渗流速度越大，其非达西渗流影响的区域越大，非达西渗流的特征也越明显.其他参数保持不变，表皮系数越大，附加压降越大，压力波传播越慢，压力及压力导数曲线位置越高，对应现场关井前的产量越大，井底污染越严重.

图6 高速非达西表皮系数Sd对曲线形态的影响

5 实例应用

为了验证模型的准确性，选取中国西部T油田某深层高产碳酸盐岩油藏作为研究对象.T油田某油藏是大型碳酸盐岩裂缝型油藏，储集、渗流空间主要为大小不同的溶蚀孔隙、微裂缝组成，埋深在4 360～5 200 m，地层压力48.20～57.60 MPa，储层非均质性严重，油藏类型和储层中裂缝分布较复杂.同时，较大的埋藏深度带来的强应力敏感和较高的关井前产量造成的近井地带高速非达西渗流对试井解释及储层参数反演带来了巨大的挑战.

通过改变储容比ω、窜流系数λ、应力敏感系数γ、高速非达西表皮系数Sd等影响参数，绘制解析解模型下的压力及导数的双对数理论曲线.将生产现场得到的压力数据点经过预处理之后，通过Bourdet算法求解压力导数，绘制实际曲线.最后通过最小二乘法等算法拟合理论曲线与实际曲线，进行参数反演并与试井商业软件计算结果进行对比.

模型基础数据如表1所示，实例井测试段生产动态如图7～8所示，解析解模型计算拟合结果如图9所示，商业软件计算拟合结果如图10所示，解析解模型与商业软件部分结果对比如表2所示.

表1 模型输入参数

续表1

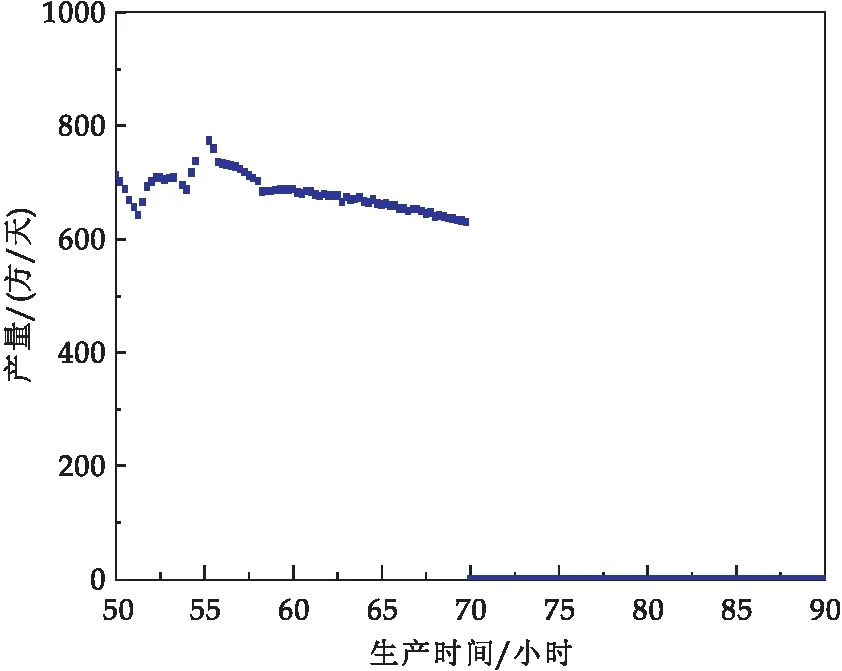
图7 实例井测试层段产量曲线

图8 实例井测试层段压力曲线

图9 解析解模型压力恢复拟合曲线

图10 商业软件压力恢复拟合曲线

表2 解析解与商业软件结果对比

由图9、图10及表2可知，压力恢复曲线出现明显的“凹子”，反映裂缝系统与基质系统之间的窜流，确定实例井测试层段为裂缝孔隙型双重介质，且解析解模型与实测井压力及压力导数曲线拟合结果更好，特别是在表皮阶段和后期曲线上翘阶段.根据解析解模型计算结果显示，弹性储容比0.16，窜流系数1.00×10-5，裂缝系统弹性储存能力较弱.此外，解析解模型能反演得到商业软件无法得到的高速非达西表皮系数为2.61，应力敏感系数为0.027，反映生产现场关井前的产量较大，同时该储层的应力敏感效应较强，驱动流体流动所需压力较高.

6 结论

本文针对深层高产碳酸盐岩油藏的强应力敏感和高速非达西两大特点，分别引入拟压力和高速非达西表皮系数来表征，通过无因次化和拉氏变换得到了拉普拉斯空间的数学模型，得到井底压力解析解，并通过最小二乘法拟合实现储层参数反演.

(1)裂缝孔隙型储层的压力响应样板曲线存在6个流动阶段，基质与裂缝的窜流阶段出现“凹子”.储容比越小，窜流现象越明显，窜流系数越小，窜流发生的时间越晚.

(2)在大埋藏深度带来的强应力敏感的影响下，储层渗流能力受到制约，压力导数曲线上移，且应力敏感强度愈强，曲线上翘幅度越大，生产现场驱动流体流动所需压力越高.同时，产量越大，对应的高速非达西表皮系数越大，附加压降越大，压力及压力导数曲线位置越高.

(3)基于T油田某实例井生产动态通过解析解模型反演得到应力敏感系数0.027、高速非达西表皮系数2.61、储容比0.16、窜流系数1.00×10-5等关键参数，现场应用实例拟合结果进一步证明了模型的准确性与实用性.