潜水一维非稳定流方程的数值求解与工程应用

李 茹，鲁海峰

(安徽理工大学 地球与环境学院，安徽 淮南 232001)

0 引言

研究潜水非稳定运动规律对于工程建设、地下水动态预报都有着重要的意义。潜水一维非稳定流方程在基坑降水水位、区域地下水流水位、沟渠流水位等预测预报方面有着广泛应用。目前众多学者针对潜水一维非稳定流方程的求解问题开展了大量的研究，如任红蕾等[1]建立了含阶梯函数型源汇项的沟渠附近潜水非稳定渗流模型，应用Laplace变换性质，求出了模型解析解，并利用数值法验证了解析解的可靠性；秦志忠[2]建立基坑降水有限元模型，探究了基坑周边水位降深变化曲线；王照亮、郭昆等[3-4]通过建立数学模型以及水文地质概念模型，利用FEFLOW数值模拟软件研究了地下水流场、分层的均衡性、潜水埋深、潜水水位；徐进、刘能胜等[5-6]基于Neuman模型，利用伽辽金法与正交解析函数族推导了解耦形式的加权余量方程式，并在编制Fortran计算程序实现数值求解的基础上，提出了潜水非稳定流的半解析数值求解格式；张年学等[7]提出了一种新的解析方法，对隔水层正倾和反倾两种情况，选取适当坐标，将含水层分为上下两部分，根据层间越流流量变化率相等原理与质量守恒定律，导出全微分方程，获得了解析解；夏强等[8]针对河渠间潜水的一维非稳定运动，考虑了补给强度的时变性，根据Boussinesq方程的第一线性化方法，应用Duhamel原理得到了方程的解析解。

上述研究成果在一定程度上对于潜水一维非稳定流方程的求解及应用起到了积极的指导作用，但联合采用解析解和数值解系统探讨此类水流方程的求解精度以便更好地指导实际工程的研究成果则较少。为此，本文采用分离变量法与有限差分法，以一类边界条件为例，系统探讨潜水一维非稳定流方程的求解方法与精度变化规律，拟为工程实践提供理论指导。

1 潜水一维非稳定流方程模型及求解

1.1 方程建立

在描述河间区域地下水流、排水沟渠等地下水头随时间变化的非稳定渗流场时，一般可建立潜水一维非稳定流方程，在初始条件下地下水头有一个二次函数形式的降深时，潜水一维非稳定流方程模型初始降深曲线如图1所示。

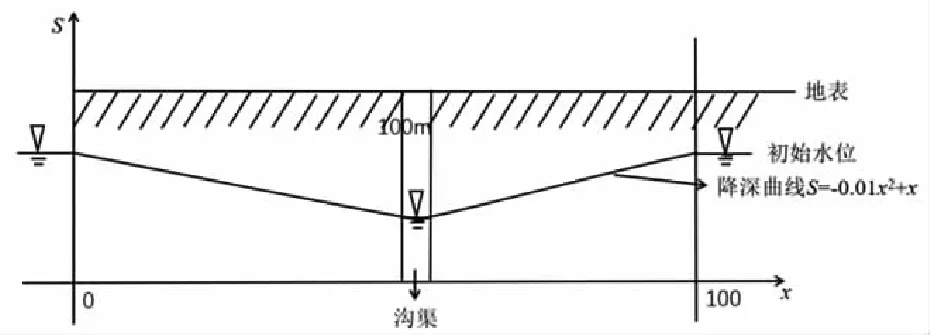
图1 一维非稳定流方程模型初始降深曲线

在一类边界条件[9]下，潜水一维非稳定流的偏微分方程及其定解条件为：

(1)

式中，T为含水层导水系数(m2/d)，μ为潜水含水层给水度，S为水位降深(m)，x为含水层宽度方向坐标(m)，t为时间(d)，L为研究潜水含水层水头降深变化的范围长度。

1.2 方程求解

偏微分方程的求解方法一般有解析法和数值法等[10]，解析法通常采用分离变量法，数值法通常采用有限差分法。本文同时采用这两种方法求解，对数值解的精度进行系统讨论和分析，并将显式差分法和隐式差分法不同网格密度的数值解与解析解进行对比。

1.2.1 解析法

由式(1)可知，该方程为二阶偏微分方程，边界条件为一类边界条件，且此边界条件为齐次[11]。所以这里采用分离变量法来求解，具体求解过程如下。

将二阶齐次偏微分方程转化为两个常微分方程。假设给定方程的解具有以下形式：

S(x，t)=X(x)T(t)，

(2)

(3)

由式(1)中的边界条件可得：

(4)

将方程(3)分为两个部分进行求解，结合给出的边界条件，根据λ取值的正负，最后推出给定问题的特征值是：

(5)

对应的特征函数分别具有以下形式：

(6)

这里Cn是任意常数。

由式(6)得到的方程通解及式(1)中的初始边界条件S(x，0)=-0.01x2+x，可得：

(7)

由此解析解方程可表示为：

(8)

取L=100 m，T=51 m2/d，μ=0.3，根据式(8)，运用Matlab软件求解出降深S随时间t变化的规律曲线，如图2所示。

图2 解析法求出的降深随时间变化的规律曲线

由图2可以看出，在一定时间内，降深S在含水层区间范围内呈规律性变化，降深在边界处的水位不变，在区间中部最大。由于含水层区间两侧有水源的径流，可补给该潜水含水层，因此降深随时间的增大而减小，经过第10 d后，最大降深已经小于5 m，水位恢复较快。

1.2.2 数值法

解析法一般只能针对方程以及边界较为简单的情形求解，随着计算机技术的飞速发展，数值法已成为偏微分方程的主要求解方法。本文分别采用显式差分和隐式差分两种方法进行数值法求解[12]，并将求解结果与解析解进行对比，进而讨论求解精度。

1.2.2.1 显式差分法

将式(1)中的x方向分成n个节点，共有(n-1)个间隔；将t分成m个节点，共有(m-1)个间隔；将偏微分方程写成差分方程，x方向步长为h，t方向步长为k。可得到如下方程：

(9)

由式(1)和方程(9)联立可得：

(10)

进一步对式(10)中的步长h和k进行变换，得：

(11)

Si，j+1-Si，j=γ(Si+1，j+Si-1，j-2Si，j)。

(12)

将式(12)变换，得：

Si，j+1=γSi+1，j+(1-2γ)Si，j+γSi-1，j。

(13)

式(13)为该模型的显式差分方程式。运用Matlab软件求解出降深S随时间t变化的规律曲线，如图3所示。

图3 显式差分法求出的降深随时间变化的规律曲线

由于显式差分法剖分的网格数会对计算结果产生较大的影响[13]，为探讨网格数对精度的影响规律，本文分别设置三种不同密度的网格。低密度网格时间t的步长为0.2 d，x的步长为10 m，结果为图3中的虚线部分，从中可以看出，在时间开始时刻即t=0 d时，函数图像曲线较为曲折，与解析法模拟出的结果相差较大；在t=6 d时函数图像曲线较为光滑，可近似拟合解析法计算结果。中密度网格时间t的步长为0.02 d，x的步长为1 m，中密度网格显式差分图像如图4所示。由图4可以看出，当方程中的参数γ≥0.5时，计算结果不收敛，无法给出方程的解，这是由显式差分法的固有缺陷造成的[14]。高密度网格时间t的步长为0.002 d，x的步长为1 m，结果为图3中的实线部分，从中可以看出，函数图像曲线整体光滑，在x=0处的同一时刻，通过此方法模拟出的结果与解析法模拟出的结果基本吻合；在接近区间中点即x=50 m时，得到的结果准确度较低。

图4 中密度网格下显式差分法计算结果

1.2.2.2 隐式差分法

由于显式差分法对网格剖分有着较高的要求，下面讨论隐式差分法的求解过程。将式(1)写为隐式差分格式，可得：

(14)

由式(1)和方程(14)联立可得：

(15)

Si，j+1-Si，j=γ(Si+1，j+1+Si-1，j+1-2Si，j+1)。

(16)

将式(16)变换后为：

(1+2γ)Si，j+1-γSi+1，j+1-γSi-1，j+1=Si，j，

(17)

式中，i=2，3，…，n-1，共(n-2)个节点。由此可建立方程组为：

(18)

根据此方程可变换为以下矩阵形式：

(19)

根据式(19)，采用追赶法在Matlab软件中进行求解，并给出降深S随时间t变化的规律曲线，结果如图5所示。

图5 隐式差分法求出的降深随时间变化的规律曲线

为探讨网格数对精度的影响规律，同显式差分法一样采用三种不同密度的网格。低密度网格时间t的步长为0.2 d，x的步长为10 m，结果为图5中的虚线部分，从中可以看出，在网格密度过低时，计算结果存在较大的偏差。高密度网格时间t的步长为0.002 d，x的步长为1 m，计算结果为图5中的实线部分，从中可以看出，随着网格数的增加，曲线更为光滑，计算结果更为精确，当t=0 d时，所呈现的曲线为初始降深，初始最大降深为25 m，随着时间的增加，在地层同一点处的降深不断减小。

为了与显式差分法进行对比，同样采用显式差分法中的中密度网格，时间t的步长为0.02 d，x的步长为1 m，结果如图6所示。对比图6和图4可以看出，隐式差分的网格剖分不受γ取值的限制，在不满足γ<0.5时，计算结果依然收敛，由此显示出隐式差分法的优越性。

图6 中密度网格下隐式差分法计算结果

1.3 结果对照

为反映各种计算方法的精确度，选取其中一组数据进行误差对比。这里选取时间为6 d时的数据，对照结果如表1所示。

表1 部分节点降深取值对照表 m

2 实例应用

下面对潜水一维非稳定流方程在一类边界下的各种求解方法进行实例运用。某地铁线路在建设施工过程中，在基坑开挖时遇到了潜水含水层，这将会对工程建设以及基坑开挖产生重大影响[15]。图7为某地铁线路建设过程中基坑开挖示意图。基坑开挖宽度为20 m，深度为15 m，长度为100 m，可视为潜水一维非稳定渗流。根据岩土勘察结果，场地潜水含水层水位埋深为3 m，含水层厚度为17 m，岩性主要为粉砂，含水层渗透系数K=5.1 m/d。工程设计时采用井点抽水方式对基坑进行降水，为准确掌握抽水停止后水位恢复情况，采用潜水一维非稳定流方程进行求解。

2.1 建立模型

假设抽水一定时间后，地下水位的降深曲线满足二次函数形式(如图7所示)，以下将讨论抽水停止后基坑水位恢复情况，其水位降深方程为：

(20)

其定解条件可描述为：

(21)

含水层渗透系数K=5.1 m/d，含水层厚度M=20 m，给水度μ=0.3，将潜水含水层线性化[16]，可得到含水层导水系数T=K(M/2)=51 m2/d。

图7 某地铁线路基坑开挖示意图

2.2 求解方程

根据前面的研究结果，采用解析法和隐式差分法进行求解，图8为隐式差分法和解析法模拟抽水停止后水位恢复的动态演变过程。

图8 某地铁线路基坑降深恢复曲线

通过图8可知，地铁工程的不同时间段对地下水位的影响程度不同。停止抽水时，该基坑地下含水层中部即x=50 m处的水头降深最大，为25 m。随着时间的变化，地下水位慢慢恢复，在停止抽水后第4 d水位恢复速率减慢，到第10 d水位基本恢复，直至最后地下水降落漏斗消失，水位恢复到初始状态，且地下水环境趋于平稳。根据结果分析可知，基坑停止抽水1 d后基坑中部水位已上升到坑底。

3 结论

(1)对潜水一维非稳定流水位降深规律进行研究，建立降深随时间变化的方程模型，借助分离变量法和有限差分法求解方程的解析解和数值解，对数值解剖分不同密度的网格，采用显式差分法和隐式差分法进行求解，以此讨论计算精度变化规律。

(2)显式差分和隐式差分求解方法的模拟结果相差不大，在相同密度网格剖分下，显式差分法较隐式差分法的求解精度要高，但显式差分法存在网格约束条件，在实际应用时需注意网格剖分密度。

(3)实例应用表明，潜水一维非稳定流方程可很好地用于实际工程，为工程建设过程中地下水渗流计算提供理论基础。