基于改进FCPM的工程项目施工动态规划研究

刘大江

(唐山学院 土木工程学院，河北 唐山 063000)

0 引言

关键路径法(Critical Path Method，CPM)是对大型复杂项目进行计划、调度与控制的重要且有效的工具[1]。传统CPM的成功实现必须基于施工规划中有清晰的活动持续时间，然而，工程项目的一次性、项目活动实现的不可重复性、实现过程的复杂性和环境的不确定性，致使工程项目活动的持续时间难以被准确预测、项目数据信息失真，从而导致施工规划或计划出现严重偏差。计划评审技术(Program Evaluation and Review Technique，PERT)也是一种安排大型复杂项目计划的管理方法，它虽引入了基于概率分布(如正态分布、β分布等)假设的三时估计法来表达项目活动持续时间的不确定性，但恰当的概率分布需要历史统计数据和人的判断确定，而不能随机假设；并且在工程实践中，尚无对活动乐观的、正常的和悲观的持续时间进行规范定义，导致相关概率分布假设很难成立。显然，以传统方式处理不确定性状态下的施工动态规划问题难以获得满意的效果，而基于模糊理论的施工动态规划被认为比基于概率论的更加有效。因此，模糊关键路径法(Fuzzy Critical Path Method，FCPM)被广泛应用于求解项目施工动态规划问题。

基于FCPM的项目施工动态规划分析需要实现三个目标[2]：(1)识别项目的最高风险活动和路径，即识别不可浮动的关键活动和关键路径；(2)计算项目最终完成时间，即总工期；(3)确定进度计划中每项活动的总时差。同时，还应当妥善解决两方面关键问题：(1)项目总工期、最早和最迟时间参数的模糊最大值或最小值运算；(2)涉及最迟时间参数和总时差的模糊减运算可能产生的不可行解。

文献[3][4]应用模糊数的符号距离排序法，求得了项目模糊网络的关键路径；文献[5]通过定义基于广义模糊数质心的排序函数，判别了最早和最迟时间参数，识别了项目模糊网络的关键路径；文献[1][6]通过建立线性规划模型，计算了时间参数的下限值和上限值，获得了每项活动最早和最迟时间的隶属函数，从而确定了项目模糊网络的关键路径和路径的关键程度；文献[7][8]通过定义模糊活动时间的关键性，以及利用通过线性规划模型计算出的路径的关键度，确定了项目模糊网络的关键路径；文献[9]采用字母序排序法对活动的模糊时间参数进行排序确定了其关键性，识别了关键路径；文献[10]通过定义将模糊数转换成实数的排序函数，实现了对模糊网络各项活动时间参数的计算和关键路径的确定；文献[11]-[14]提出利用距离测度的排序法计算每个活动的模糊时间参数，确定了项目网络关键路径和总工期。

上述研究不同程度地解决了模糊数最值运算和关键路径识别问题。文献[3]-[10]均采用先将模糊数转换为实数再进行比较的模糊数的弱比较方法确定项目模糊网络的关键路径，但这种方法使数据的原始信息损失大，且规避了相关时间参数的计算，不能有效实现项目施工动态规划分析的全部目标；文献[11]-[13]给出了距离测度公式，对于两个完全相等的模糊数应用其计算出的距离却大于零，这与事实相悖，同时，这些文献均未考虑活动持续时间模糊状态下关键路径可能发生变化的事实。文献[14]提出了基于理想点的距离测度公式，虽在一定程度上弥补了上述研究的不足，但与最大和最小理想点距离同时相等的两个模糊数却无法比较大小。另外，针对在最迟时间参数和总时差计算过程中规避模糊减运算可能产生的不可行解问题，学界也开展了大量卓有成效的研究，比如在应用交互式模糊减法[15-16]、求解模糊方程法[17]、线性规划法[18]、扩展模糊算术运算模型[19]、新多项式算法[20]、八角形模糊减法式[21]等方法时由于注意增设了非负约束条件，故均不同程度地规避了模糊减运算产生的不可行解问题，然而这些研究由于未考虑模糊数偏序关系与左右展宽的非负约束等情况，模糊减运算产生的不可行解问题尚未得到有效解决。

鉴于此，本文提出一种基于向量集成相似度排序算法和修正的模糊减运算标准算法的改进的FCPM，以提高项目施工动态规划分析的合理性和有效性。

1 梯形模糊数基础理论

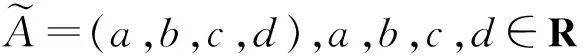
(1)

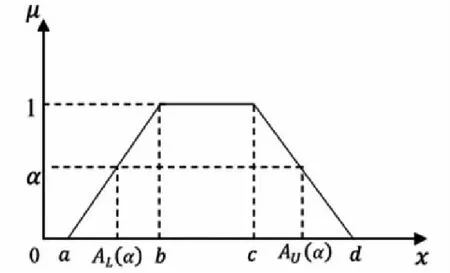
图1 梯形模糊数

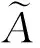
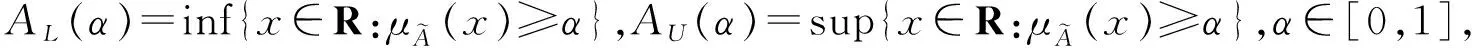
(2)

Aα+Bα=[AL(α)+BL(α)，AU(α)+BU(α)]；

(3)

Aα-Bα=[AL(α)-BU(α)，AU(α)-BL(α)]；

(4)

λAα=[λAL(α)，λAU(α)]，λ∈R且λ≥0；

(5)

max(Aα，Bα)=[max(AL(α)，BL(α))，max(AU(α)，BU(α))]；

(6)

min(Aα，Bα)=[min(AL(α)，BL(α))，min(AU(α)，BU(α))]。

(7)

2 改进的FCPM

2.1 向量集成相似度排序算法[23]

向量集成相似度排序算法是利用梯形模糊数的等效参数形式，通过区间数与二维向量的信息转换，集成比较信息向量与理想信息向量的范数相似度和方向相似度的信息，客观、综合地反映比较信息向量与理想信息向量相似程度，以确定梯形模糊数大小的一种排序方法。

向量集成相似度排序算法主要解决的是模糊施工动态规划分析中递推计算活动最早和最迟时间参数、识别关键活动和关键路径、确定总工期等问题。

2.1.1 确定转换信息向量

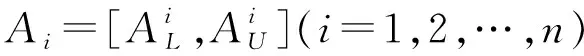
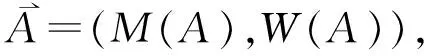
(8)

显然，任意一个区间数X均可用M(X)和W(X)描述，那么对于区间数A和B，当且仅当M(A)=M(B)且W(A)=W(B)时，A=B。

2.1.2 确定理想信息向量

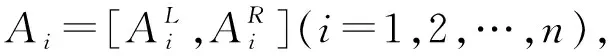
(9)

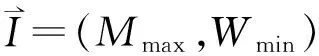
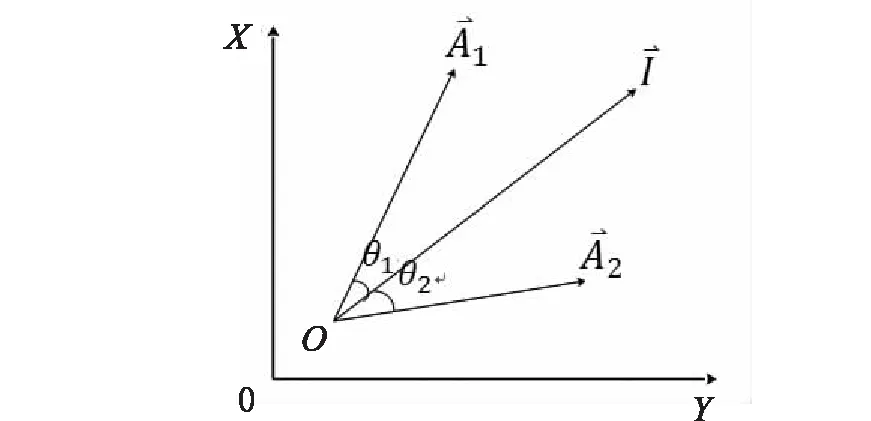
图2 比较信息向量与理想信息向量

2.1.3 计算向量集成相似度

2-范数为：

(10)

内积为：

(11)

夹角为：

(12)

范数相似度为：

γ=

(13)

方向相似度为：

(14)

集成相似度为：

(15)

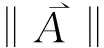
2.1.4 模糊数排序

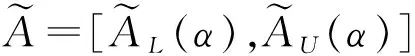
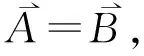
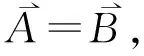
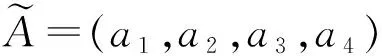
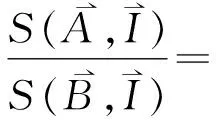
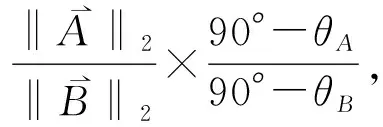
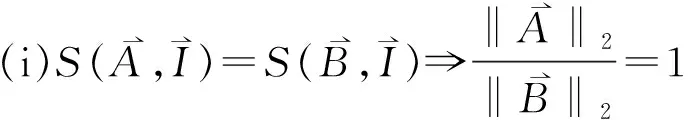
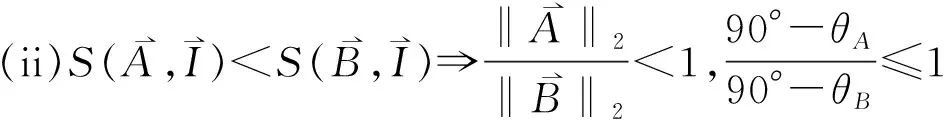
因此，定理2成立。

基于式(10)-(15)，逐一计算并比较每个比较信息向量与理想信息向量的集成相似度。由定理2可知，集成相似度越大，其对应的模糊数相对越优，从而完成对模糊数的排序。

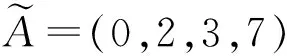
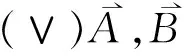
2.2 修正的模糊减运算标准算法[22]

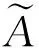
模糊减运算标准算法[29]：

(16)

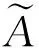
虽然计算获得了非负解，但其明显与区间数定义中AL≤AU的规定相悖，致使计算结果毫无实际意义。因此，将式(16)修正为式(17)。

(17)

3 改进的FCPM施工动态规划分析的实现

改进的FCPM施工动态规划分析的实现过程与CPM一致，但需要应用梯形模糊数和相关代数进行运算，本文以单代号网络计划为例阐述其实现过程。单代号网络计划的节点信息一般包括：活动名称(N)、节点编码(i)、活动持续时间(Di)、最早开始与结束时间(ESi与EFi)、最迟开始与结束时间(LSi与LFi)和总时差(TFi)，如图3所示。

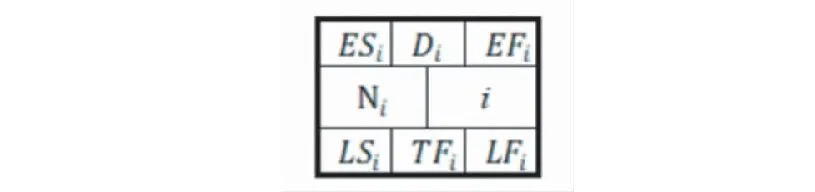
图3 单代号网络计划的活动节点

基本步骤如下：

Step 1 构建项目施工模糊网络。

选择网络计划类型，确定每项活动的逻辑关系与活动模糊持续时间，设置虚拟开始节点(Sn)和结束节点(En)。活动持续时间以梯形模糊数的等效参数形式表示，虚拟开始节点：DSn=[0，0]，ESSn=[0，0]，EFSn=[0，0]。

Step 2 枚举模糊网络的全部路径并计算每一路径上活动持续时间之和。

根据式(3)进行模糊加运算，设模糊网络存在m条路径，则路径x的持续时间之和为：

(18)

Step 3 识别模糊网络关键路径并计算项目总工期。

关键路径判别标准：活动持续时间之和最长的路径是关键路径。

关键活动判别准则：关键路径上的活动均为关键活动。

项目总工期：

T=max(Tx)。

(19)

Step 4 计算活动的最早开始与结束时间。

活动i在路径x上的最早开始时间：ESxi=EFxh，h∈pred(i)，其表达如图4所示。

图4 活动i在路径x上的最早开始时间

活动i的最早开始与结束时间分别按式(20)(21)计算，其表达如图5所示。

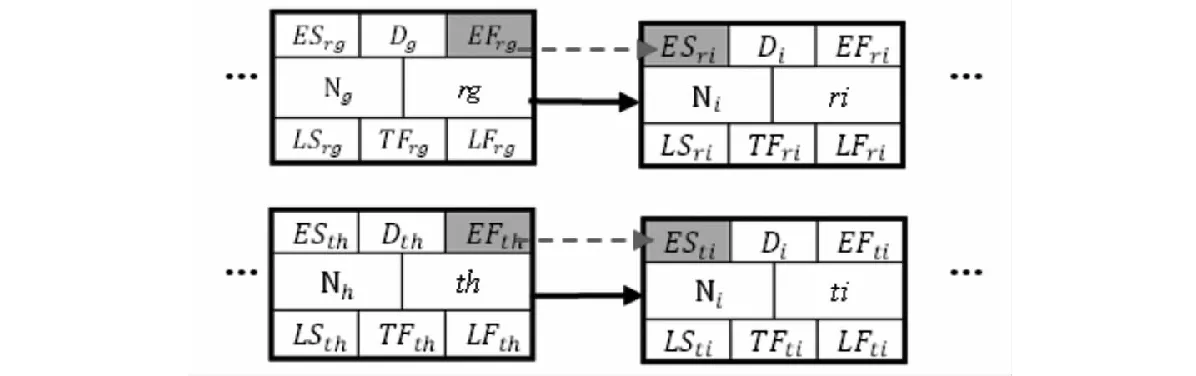
图5 活动最早时间

(20)

EFi=ESi+Di。

(21)

Step 5 计算活动的最迟开始与结束时间。

虚拟结束节点：DSn=[0，0]，LFSn=[EFEn，EFEn]，LSSn=[EFEn，EFEn]。模糊减运算据式(17)，逆向递推计算模糊最迟开始与结束时间，如式(22)(23)所示，其表达见图6。

(22)

LSi=LFi-Di。

(23)

图6 活动最迟时间

Step 6 计算活动的总时差。

TFi=LSi-ESi或TFi=LFi-EFi。

(24)

Step 7 活动持续时间模糊状态下的关键路径变化情况分析。

根据不确定状态下α∈[0，1]的变化情况，描绘各条路径的变化轨迹，并对关键路径变化情况作出分析。

4 实证分析

某项目为预制装配式混凝土(PC)剪力墙结构。承包商试图通过合理地确定总工期和关键路径，制定科学的施工动态规划，有效识别与规避施工风险，优化配置施工资源。以该项目标准层PC叠合楼板的施工为例，利用改进的FCPM进行施工动态规划分析。

依据PC叠合楼板施工工艺及特点，构建单代号施工网络(A-on-N)，如图7所示，活动的逻辑关系为FTS。通过专家对既有类似项目(相同或相近的结构类型、施工方式、建设规模和质量标准等)活动持续时间数据的统计与测算，并充分考虑承包商施工水平和工作效率，获得以梯形模糊数表示的该项目活动的持续时间。例如，经统计的类似既有项目A-J中“PC楼板吊装”的持续时间如表1所示。经专家综合分析确定“PC楼板吊装”模糊持续时间为(1，2，3，4)。

图7 某项目标准层PC叠合楼板的施工网络

表1 类似项目中“PC楼板吊装”的持续时间 d

同理，其他活动的模糊持续时间(为简化计算均取整数)和逻辑关系(FTS)如表2所示。

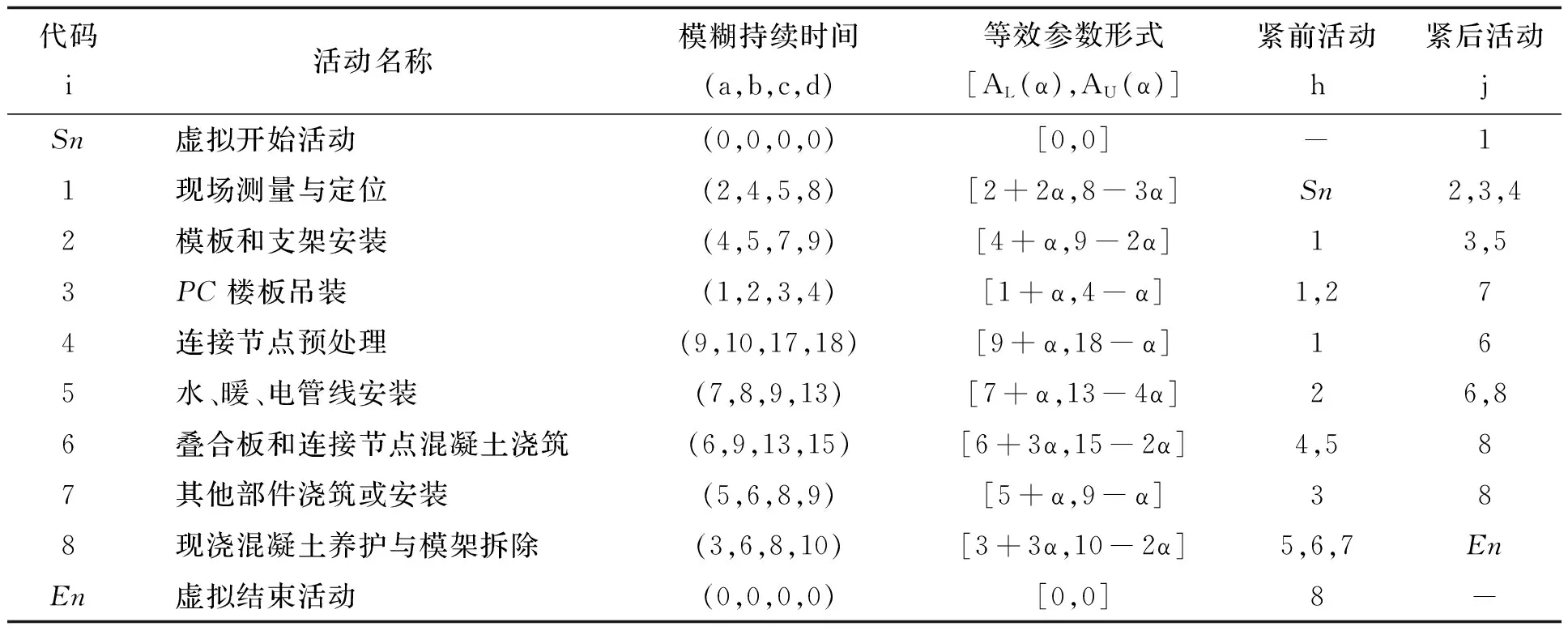
表2 活动模糊持续时间和逻辑关系 d

基于改进的FCPM的PC叠合楼板施工动态规划分析的实现过程如下：根据式(2)实现PC叠合楼板施工网络的梯形模糊活动持续时间的等效参数形式转换，如表2所示。枚举PC叠合楼板模糊施工网络的全部路径，计算其对应的持续时间，如表3所示。

表3 模糊施工网络路径及其持续时间

根据式(18)(19)，不同α∈[0，1]水平下PC叠合楼板施工的总工期和关键路径如表4所示。

表4 不同α水平下的项目总工期和关键路径

表4显示：α由0.2变化为0.3时，关键路径从1-4-6-8转换成1-2-5-6-8(如图8所示)，项目总工期和时间参数均随不同α水平而发生改变。当α取(0.2，0.3)中某一值时，路径1-4-6-8和1-2-5-6-8的信息向量具有完全相等的集成相似度，二者均为关键路径。这表明，在活动持续时间模糊状态下，施工网络是动态的，关键路径和项目总工期随不同α水平的变化而改变，而且模糊施工网络可能同时存在多个关键路径。该项目施工网络的路径变化情况如图9所示。

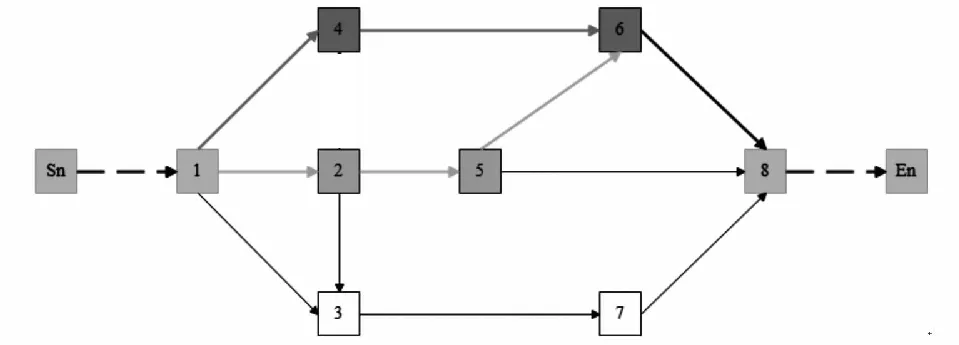
图8 关键路径的转换轨迹

图9 不同α水平下施工网络的路径变化情况

5 结论

基于向量集成相似度排序算法与修正的模糊减运算标准算法的改进的FCPM成功实现了施工动态规划分析的三个目标，通过定义梯形模糊数等效参数形式，可靠地实现了施工动态规划由模糊性向确定性的转化；向量集成相似度排序算法有效解决了模糊项目总工期、最早与最迟时间等参数计算的模糊最值问题；修正的模糊减运算标准算法最大限度地消除了模糊减运算结果的任意扩张，显著降低了计算过程中数据原始信息的损失，并合理消除了不可行解的产生；关键路径枚举法在简化计算工作的同时，可快速确定关键路径和项目总工期；至关重要的是，对模糊持续时间状态下关键路径的变化情况进行剖析，无疑将进一步提高施工动态规划分析的客观性。实证分析表明，改进的FCPM计算和推理简单、适应性和可操作性强。

然而，此改进的FCPM对于快速准确地枚举大型复杂项目网络的全部路径仍存在一定困难，需协同BIM、人工智能等技术开发工程项目施工动态规划智能分析系统，以进一步提升工程项目施工动态规划分析的绩效和水平。