环形混凝土截面压弯承载力逆算法的解析解

章胜平 陈 旭 兰树伟

(1. 昆明理工大学 建筑工程学院， 昆明 650504； 2. 昆明学院 建筑工程学院， 昆明 650214)

圆形或环形混凝土截面具有美观、风阻小、水流阻力小等优点，采用离心法、快速抽芯法工艺施工经济，在现浇或预制柱墩、管柱、管桩中应用日益广泛[1]．现有规范圆形或环形截面压弯承载力计算简化公式存在一些假定条件[2]，不是精确解．如，圆形或环形混凝土截面公式假定为均匀配筋，而在实际工程中，抗滑桩、支护桩、桥墩等圆形或环形构件具有直径大、弯曲方向单一并且方向明确的特点，若均匀配筋，受压区、中性轴附近钢筋应力小，造成材料浪费和经济损失[3]．混凝土等效矩形应力模型是基于矩形截面假定，在等效合力假定条件下圆形或环形截面合力比矩形截面更靠近中性轴[4]，若再假定相同合力位置则高估了承载力，偏于不安全．另外，规范简化公式是以受压区高度对应的圆心角为未知量，简化公式不是圆心角的单调函数，在迭代法程序中，若假定的圆心角初值不在精确解附近则可能造成难以收敛或不收敛情况．

文献[5]给出圆形和环形截面抗滑桩的非均布配筋计算方法，但没有考虑矩形截面假定对等效矩形应力参数的影响．环形混凝土截面除了考虑截面宽度非线性，还应考虑受压区与内圆之间的关系[6-7]．压弯承载力计算准确性取决于混凝土等效应力计算的准确性，美国ACI协会研究报告[8]分析了高强混凝土实验结果反算得到的等效矩形应力参数，文献[9]基于理论推导提出了等效三角形应力的一套参数，文献[10]对应变梯度影响的等效矩形应力参数进行了实验研究，文献[11]对非矩形截面参数进行了实验研究．为此，本文按照由应变计算内力的逆算法(不需要迭代)，基于数值条带逆算法，理论推导了环形混凝土截面等效矩形应力参数的一套解析解，获得环形截面均匀、非均匀、对称、非对称配筋压弯承载力计算的统一电算方法．

1 解析解推导

本文解析解推导基于逆算法[12-13](已知应变求内力)，在数值条带法基础上，进一步将应力-应变本构方程代入积分，解析求解积分，计算内力再反算等效矩形应力参数，获得解析解．

1.1 正截面承载力计算逆算法

逆算法不同于数值迭代法，不需要假定应变．数值迭代法也称为应变协调分析，当截面特性和轴力(N)已知时，假定应变3～5次，钢筋应力按照本构关系曲线，混凝土应力按照本构曲线或等效矩形应力块，若所假定应变满足轴力平衡方程的允许误差(δ)，则由应变求出弯矩(M)极限值，如图1(a)所示．数值迭代法需要软件操作人员知晓如何假定应变，理解允许误差，能根据承载力合理调整允许误差大小，对结果具有一定的判断能力．虽然该法比现有规范简化方法更精确，但用于实际工程不方便．

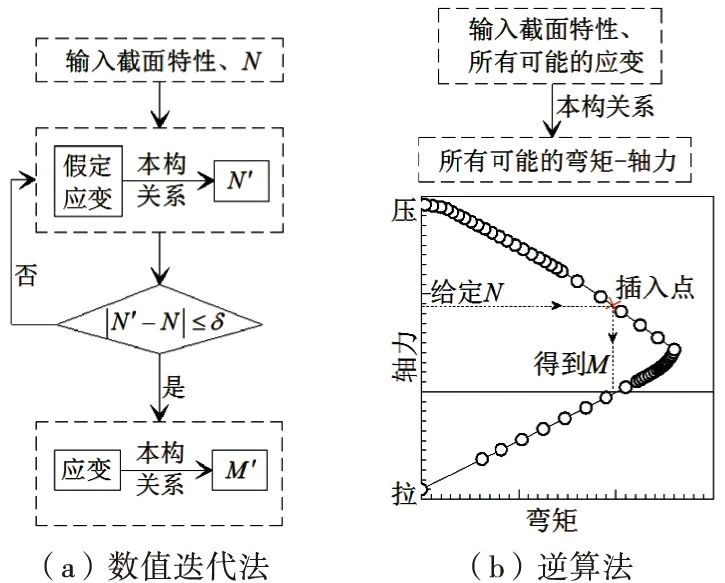
图1 正截面承载力计算

逆算法是已知截面特性，按照极限状态所有可能的应变，按照本构曲线，得到所有可能的弯矩-轴力极限值．利用插入法函数，获得已知轴力对应的弯矩极限值，如图1(b)所示．计算过程中积分求解能用数值积分(1.2节)，也能用解析法(1.3节)．解析法用普通计算机程序计算仅需1～2 s．数值法电算时间略多于解析法，与条带划分数量有关，条带划分数量对结果的精度也有影响．数值法能用于迭代算法，也能用于不迭代算法，本文数值法指基于逆算法的数值积分条带法(不需要迭代)．

1.2 等效矩形应力参数的积分公式

分别以环形截面外圆圆周和内圆圆周几何坐标为变量(见图2(a))，建立圆心角与应变之间的关系

(1)

式中：ε为圆心角θ对应的外圆应变；εi为圆心角θ对应的内圆应变；εc1为下缘应变；εc为上缘应变；r为无量纲化外圆半径；ri为无量纲化内圆半径；R为外圆半径；Ri为内圆半径，下标i表示内圆．

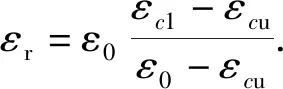
图2(b)五个应变区域表示了极限状态所有可能的应变，从区域①变化至区域⑤，混凝土受压边缘应变εc可能小于极限值，钢筋(受拉)也可能未屈服．按照图2(b)五个应变区域，确定式(1)应变εc1和εc的取值，可得正截面承载力所有可能的弯矩-轴力极限值[14]．这五个区域按照应变变化规律划分，从轴心受拉开始，最终到达轴心受压．区域①中εs固定为极限应变(1%)，εc由1%变化至0；区域②εs固定为极限应变(1%)，εc由0至极限应变(εcu)；区域③εc固定为εcu，εs由1%至εy；区域④εc固定为εcu，由εs为1%至εc1为0；区域⑤εr固定为ε0，εc由εcu至ε0．区域①全部受拉，属于小偏心受拉的范围；区域①、②界限为大、小偏拉临界；区域②、③属于大偏心受拉、纯弯、大偏心受压；区域③、④界限为大、小偏压临界；区域④、⑤属于小偏心受压；区域⑤全部受压．

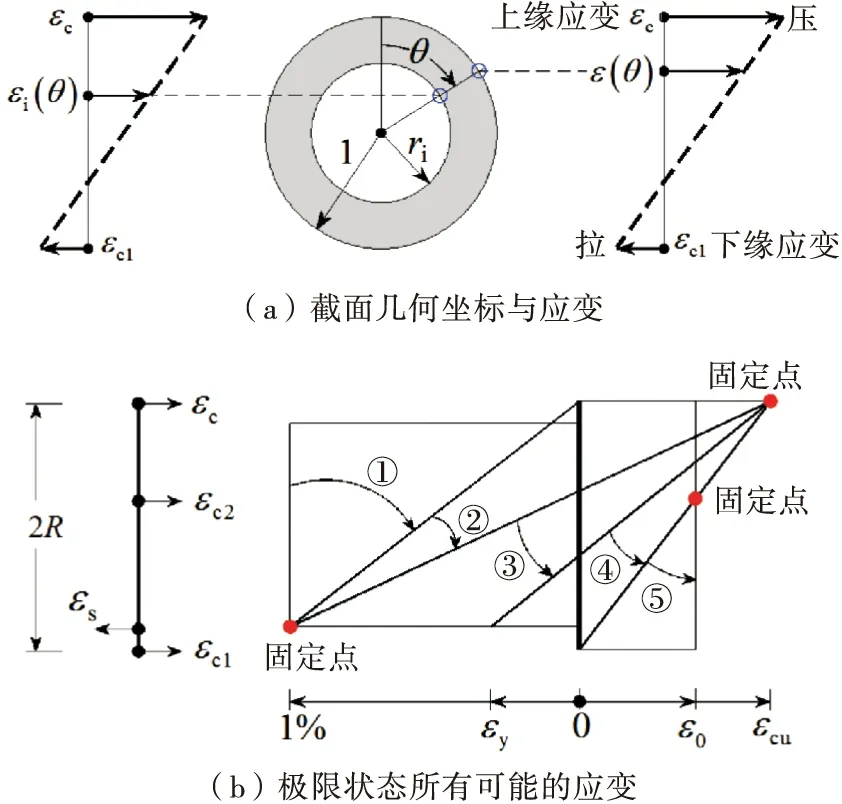
图2 应变图

(2)

式中：ε0为混凝土轴压应变极限；fc为混凝土轴心抗压强度．

则，混凝土应力与应变之间的关系可表示为

(3)

式中：εcu为混凝土压弯应变极限．

需要说明的是，式(3)第1式表示混凝土受拉时应力为0，这是较多混凝土结构设计规范对正截面承载力计算所采用的基本假定．由此假定可知当应变位于图2区域①时(小偏心受拉区)，混凝土应力为零，拉力完全由钢筋承担，因此本文的混凝土等效矩形应力参数对此区域不做分析．

假想环形截面内圆充满同样的材料，则环形截面内力等效于外圆内力减去内圆内力，如图3所示．

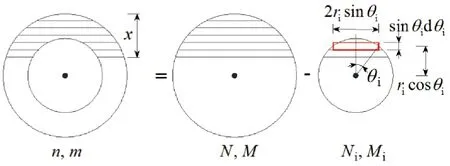
图3 内力计算

沿高度方向将截面划分为若干个条带，条带宽度、高度和偏心距如图3所示，则外、内圆轴力(N)与弯矩(M)分别为

(4)

(5)

无量纲化轴力(n)和弯矩(m)分别为

(6)

(7)

已知轴力和弯矩，可以反算设计参数．环形与矩形截面不同，混凝土合力位置不在矩形应力块高度中点，有受压区高度系数还需再计算合力位置．因此本文参考德国规范[15]，假定受压区高度系数β1=1，即虚拟应力块高度=真实受压区高度．等效矩形应力参数选择应力参数α和力臂参数k，其优点是按照力臂参数可以直接建立弯矩方程，这对非矩形受压区设计使用更方便．α和k计算式为

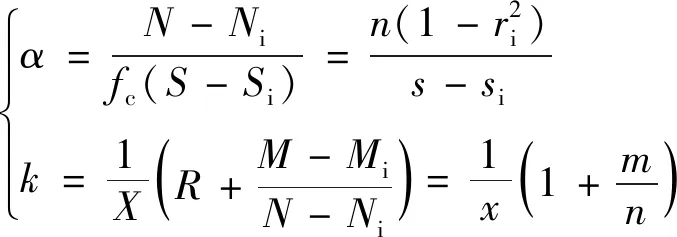
(8)

式中：S和Si分别为外圆受压区面积和内圆受压区面积；X为受压区高度；s、si和x分别是这3个变量的无量纲化．

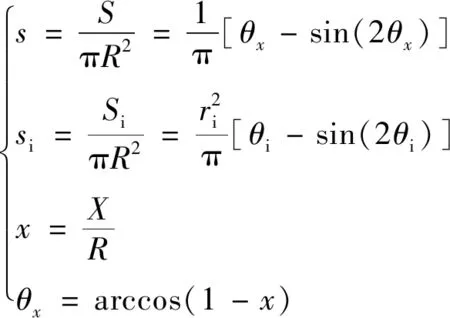
(9)

内圆圆心角与受压区的位置有关，受压区高度可能在内圆上部、内圆范围或者包括整个内圆，因此内圆圆心角有3种情况(如图4所示)．内圆圆心角计算公式为

(10)

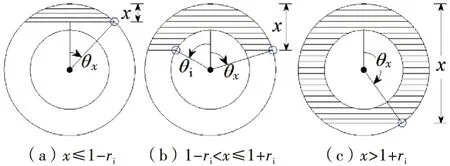
图4 3种受压区

将式(6)、(7)数值积分，代入式(8)得到设计参数的数值解．数值积分是一种相对精确计算方法，如图5所示．

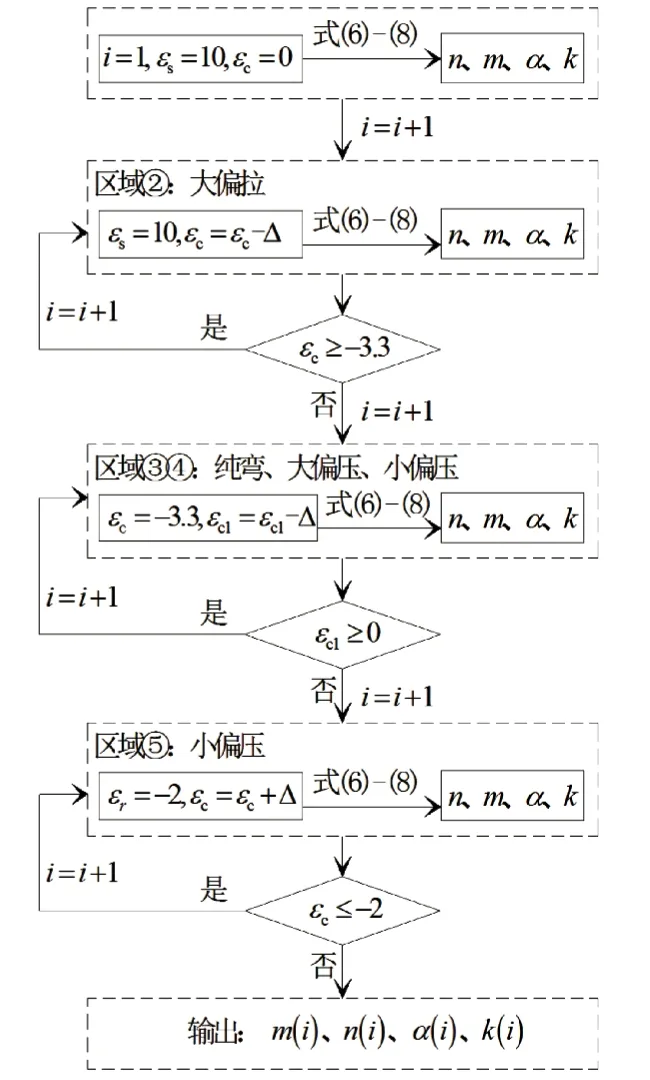
图5 数值法计算框图

为了分析数值法计算的特点，计算分析了条带划分数量对参数的影响，结果如图6所示．计算中采用了如下假定条件．

1)ri=0.7，ε0=-2‰，εcu=-3.3‰，εy=2.175‰．

2)下缘钢筋与截面近边缘距离as=0.2R．

图6 条带数量的影响

从图6可以看出，随着条带数量增加，α和k在收敛，说明编程正确．对于α，30个条带和100个条带两条曲线几乎重叠(如图6(a)所示)，说明α对条带划分数量不太敏感．对于k，30个条带曲线数据波动大，100个条带曲线数据波动较小(如图6(b)所示)，说明k对条带划分数量敏感．由此可见，数值法在软件应用时，使用者需要知晓什么变量对结果影响大．另外，在设计中提供多种方法，还能用于结果的相互验证．

1.3 等效矩形应力参数的解析解

数值法是采用数值积分(如梯形法)计算内力公式的积分，解析法则是将应力本构方程代入积分，解析求解，获得解析解．在数值法基础上，解析法还须进一步考虑应力分段函数、受压区范围等情况，根据不同情况推导相应的解析解．环形截面解析解推导，建立在圆形截面基础上，圆形截面应力图分为图7所示的3种情况．

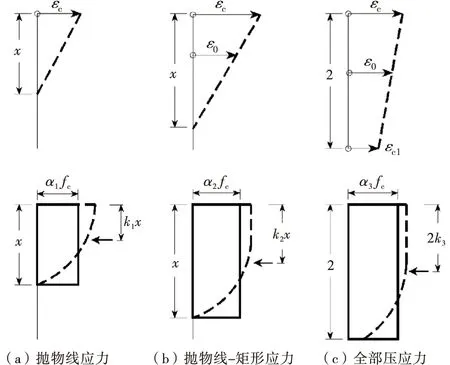
图7 3种应力图

对3种应力图，假设参数α1和k1表示抛物线应力情况解析解，α2和k2表示抛物线-矩形应力情况，α3和k3表示全部压应力情况．将式(3)代入式(6)、(7)，化简、整理，得到圆形截面等效矩形应力参数的解析解

立体几何的学习，一般体现为“直观感知——操作确认——思辨论证——度量计算”这样一个认知过程．本题给出图形便于学生感知，第一问要求学生进行论证，并在此基础上进行度量计算，考查学生的观察、想象、分析、判断及推理能力．立体几何的学习需要学生具备必要的空间想象能力、推理论证能力和运算能力，这对于学生后继学习具有重要意义，更是相关技术职业工作必不可少的基础能力．

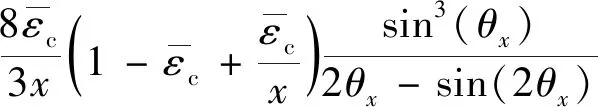
(11)

(12)

(13)

(14)

(15)

(16)

式中：θ0为图7(b)、(c)所示应变ε0对应的圆心角．

利用外圆、内圆参数解析解，得到环形混凝土截面等效矩形应力参数解析解

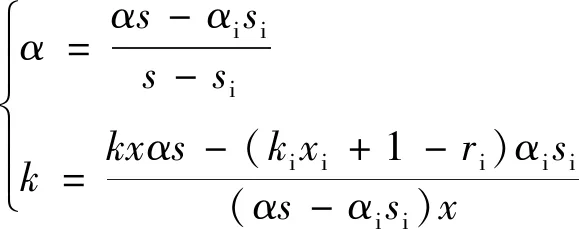
(17)

解析法计算框图是在数值法框图基础上，利用解析解计算弯矩、轴力和参数．在选择公式时，解析法设置条件语句，如上缘应力未塑化选择公式(11)、(14)，上缘应力塑化选择公式(12)、(15)．从计算公式看，解析解公式冗长复杂，推导或程序编制过程，可能出错，因此需要与数值解不断地对比、校正，以获得最终正确的解析解．另外，相比规范简化方法，解析解是精确解．解析解能用于软件设计，也能用于简化方法推导与验证．

1.4 解析解验证

按照图6假定条件，采用解析法计算等效矩形应力参数，结果如图8所示．从图8可见，数值解收敛于解析解，由此解析解获得验证．

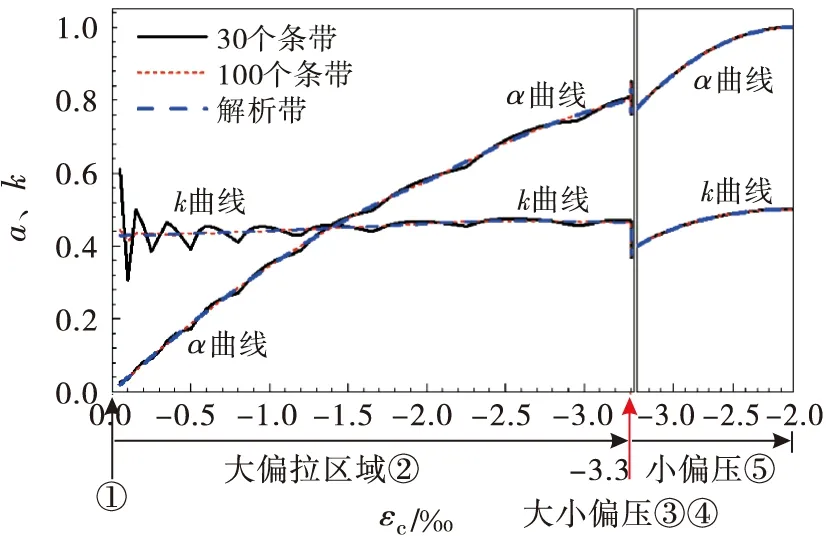
图8 解析解的验证

另外，从图8曲线数值分析还可以看出：

1)应力参数α曲线变化幅度较大，从0变化至1，力臂参数k曲线变化幅度小，数值在0.4左右．

2)当混凝土上缘应变达到极限值(εc=-3.3‰)，纯弯、大偏压和小偏压破坏的区域③和④，α曲线数值为0.76至0.845，k曲线数值为0.37至0.465．

3)小偏压破坏的区域⑤，随着偏心距减小趋近于轴心受压，α曲线数值从0.78逐渐增加趋近于1，k曲线数值从0.4逐渐增加趋近于0.5．

2 解析解算例

基于1.3节等效矩形应力参数解析解，钢筋按照应变计算应力，能够实现均匀、非均匀、对称、非对称配筋压弯承载力计算的统一公式，即

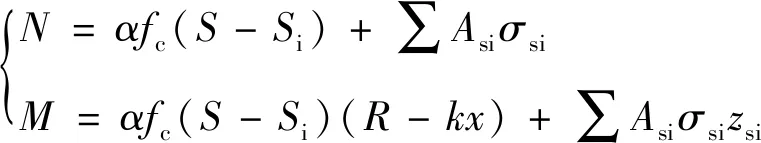
(18)

式中：Asi、σsi和zsi分别表示第i根钢筋的截面面积、应力和高度坐标，高度坐标以形心轴为原点，向下为正．

需要说明的是，通常简化方法将受力钢筋等效为钢环，这存在一定程度的简化，而实际上在应变已知的条件下对每根钢筋单独计算应力、内力在程序实现上没有难度，因此式(18)对钢筋内力采用直接叠加法．

已知非对称配筋环形混凝土截面受弯构件(如图9所示)，仅在受拉区120°角范围内均匀布置7根Φ22钢筋(受拉钢筋截面面积As=2 661 mm2)，其它部分配置构造钢筋，钢筋抗拉强度设计值fy=360 N/mm2，钢筋受拉屈服应变εy=1.8‰，混凝土抗压强度设计值fc=14.3 N/mm2．

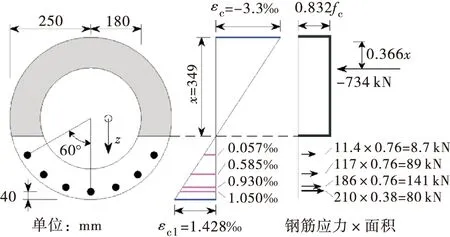
图9 压弯承载力算例

假设截面为区域④的小偏压状态，εs=-1.05‰，εc=-3.3‰，按照自编程序进行压弯承载力计算，则应力参数α=0.832，力臂参数k=0.366，应变和应力结果如图9所示，轴力Nu=-145 kN(受压)，弯矩Mu=150 kN·m．

3 结 论

按照正截面承载力计算的逆算法，不需要迭代，推导了环形混凝土截面混凝土应力设计参数解析解，建立了均匀、非均匀、对称、非对称配筋压弯承载力计算的统一公式，可以获得下列结论：

1)解析法公式虽然复杂，但解析解是精确解，数值解收敛于解析解，本文推导的解析法提供了一种工程实用设计的电算方法．

2)非矩形受压区截面等效应力模型，合力位置不在受压区高度中点，假定受压区高度系数=1，设计参数选择应力和力臂参数，设计使用更直观．按照不同受力的可能应变计算，设计参数不是常量，应力参数从0变化至1，力臂参数约为0.4．

3)以应变为已知量，单独计算钢筋内力再叠加，不需要转化为等效钢环．