基于改进WOA-BP神经网络的水电机组ADC效能评估

王康德 刘文泽 陈 泽 秦 强 匡 佩 余 涛

(华南理工大学 电力学院， 广州 510641)

随着新能源电网的快速发展，水电设备规模迅速扩大，水电设备成为水电站最主要的资产，水电站正从传统设备管理模式转向全生命周期设备管理模式[1-2]．在全生命周期管理模式中，效能评估起着关键作用[3]．相较于传统可靠性评估，效能评估不仅考虑了设备的安全性，而且同时将设备的性能和工作能力纳入考量，可以更加科学全面地对设备进行评估．

当前效能评估主要运用在武器装备评估领域．ADC(availability dependability capability)效能评估法由美国工业界武器系统效能咨询委员会(WSEIAC)于1965年提出[4]，综合评估可用度、可靠度和能力对武器装备作战效能的影响．Gui[5]提出了一种适用于无人装备的作战效能评估模型，基于ADC模型建立了效能评估方程和计算方法．Zhang等[6]鉴于ADC模型的目标不能充分评估民用无人机系统的有效性，结合无人机输电线路检查的要求，对其进行了改进，强调了运行条件和环境适应因素的影响，建立了完善的静止无人机系统效能评估模型．曹杨[7]提出将ADC模型引入电力设备采购，基于电力设备与武器系统之间的相似性和可比性论证了基于LCC的ADC效能评估方法的科学性．何玉钧等[8]将ADC模型引入电力通信网效能评估，尝试将该模型应用于电力设备评估，但仅将故障率设置为定值，并未考虑电力设备在时间尺度下故障率的变化．马威[9]通过威布尔分布和役龄回退模型，考虑了不同时间下故障率的变化，但回退计算公式和役龄回退因子设计较为主观，且在实际生产中，相同检修类型对于同一电力设备的多次检修也会产生不同的维修效果，导致故障率拟合预测不准确．

本文以水电机组为研究对象，使用ADC模型，并结合改进WOA-BP神经网络，建立基于改进WOA-BP神经网络的水电机组ADC效能评估模型．模型通过可用性、可信性和固有能力3方面对水电机组进行全生命周期效能评估，并考虑设备检修的影响，使用改进WOA-BP神经网络对水电机组故障率进行拟合预测，防止故障率拟合预测的主观性，使水电机组的效能评估更加准确，对其全生命周期管理更具指导作用．

1 水电机组ADC效能评估模型

1.1 水电机组效能评估体系

由于水电机组的考核标准主要集中于对调峰调频任务的评估，故本文依据武器系统效能ADC模型，并考虑水电机组并网运行调峰调频任务的应用场景，建立如图1所示的水电机组效能评估体系．

图1 水电机组效能评估体系

水电机组本身运行状态的可用性分析，使用可用时间作为可用性的评估变量；考虑水电机组对调峰调频运行任务的完成概率，设置可信度指标以反映其调峰调频的可靠程度，由故障率来反映正常或故障状态对调峰调频任务的概率差异，表示在执行调峰调频任务中保持正常运行或突发故障的概率情况；水电机组固有能力指标在调峰调频场景下主要表征为任务的响应能力与达标效果．

水电机组效能评估模型通过可用性、可信度和固有能力3个方面来计算水电机组的效能，其解析表达式为

E=A×D×C

(1)

式中：E为水电机组的效能值；A为水电机组可用性矩阵；D为水电机组可信度矩阵；C为水电机组固有能力矩阵．

1.2 可用性矩阵

对于水电机组，设定其存在两种状态：正常和故障状态．水电机组可用性矩阵可以表示为

A=[α1α2]

(2)

式中：α1为水电机组开始运行时处于正常状态的概率；α2为水电机组开始运行时处于故障状态的概率．

对于可用性矩阵中的元素：

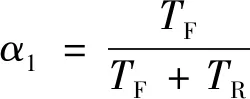
(3)

α2=1-α1

(4)

式中：TF为水电机组平均故障时间间隔；TR为水电机组平均修复时间．

1.3 可信性矩阵

根据水电机组设置的两种状态，可信度矩阵可以表示为

(5)

式中：dij表示从i状态变更为j状态的概率；1为正常状态；2为故障状态．

水电机组满足马尔可夫状态转移过程[10-11]，且机组故障后无法自发地恢复至正常状态．则水电机组的可信度矩阵为

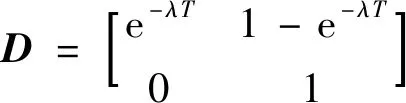
(6)

式中：λ为水电机组故障率；T为水电机组运行任务时间．

1.4 固有能力矩阵

考虑到水电机组最主要的任务是调峰调频，并参考某电网公司水电机组考核标准及文献[12-14]，本文选取一次调频投运率、响应目标偏差、调频死区、一次调频响应上升时间、一次调频响应滞后时间、一次调频稳定时间、上调峰深度和调峰贡献率作为水电机组固有能力指标．各指标上下限见表1．

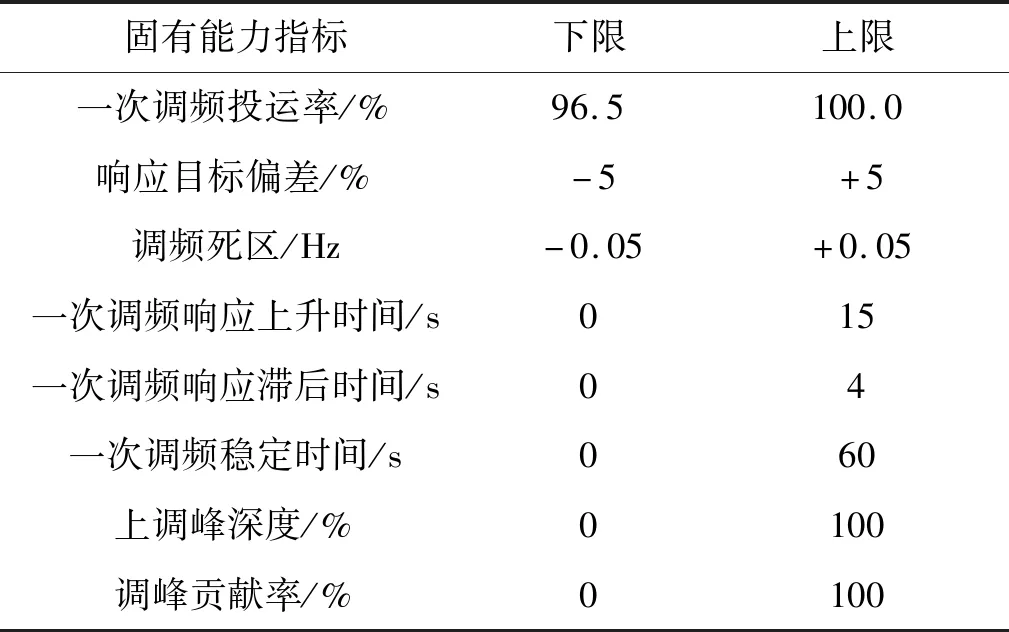
表1 固有能力指标阈值

使用极值标准化法分别对各个指标进行归一化处理，采用AHP层次分析法对各个指标进行赋权，并结合模糊评价法建立隶属度矩阵，计算得到水电机组固有能力矩阵C为：

C=w×RT

(7)

式中：w为权重矩阵；R为隶属度矩阵．

2 基于改进WOA-BP神经网络的水电机组故障率预测模型

实际生产过程中，水电机组经常受到检修的影响．本文运用改进WOA-BP神经网络模型，考虑检修和检修疲劳的影响，将检修类型分为大修、小修和不检修3种，以水电机组役龄、检修类型、检修次数和水电机组健康状态得分作为模型输入，对水电机组故障率进行拟合预测，将检修效果准确地量化为故障率变化．

2.1 BP神经网络

BP神经网络是典型的多层前向型神经网络[15-16]，其算法通过正反向传播来寻找实际值与预测值之间的误差函数最小值，利用最速梯度下降法来不断调整各神经元的权值．BP神经网络的结构如图2所示．

图2 BP神经网络结构图

BP神经网络由输入层、隐含层和输出层组成，数据通过输入层按照相应权值传递至隐含层，经过非线性处理，最终作用到输出层，输出层通过误差函数对各权值和阈值进行调整，缩小实际值与预测值的误差．

2.2 WOA算法

WOA(whale optimization algorithm)算法是近年来提出的一种模拟自然界座头鲸捕食行为的智能启发式算法[17-18]．根据座头鲸的气泡网觅食方式，其算法包括3个部分：包围猎物、泡网攻击和搜索猎物．

1)包围猎物：座头鲸在包围猎物时选择最优位置移动，其计算公式为

D*=|C*Y(l)-X(l)|

(8)

X(l+1)=Y(l)-A*D*

(9)

A*=2αr-α

(10)

C*=2r

(11)

式中：l为迭代次数；A*、C*为系数向量；Y为猎物位置向量；X为其他鲸鱼位置向量；α是收敛因子；r是[0，1]之间的随机数．

2)泡网攻击：通过收缩包围机制和螺旋更新位置来模拟座头鲸的泡网攻击行为，其计算公式为

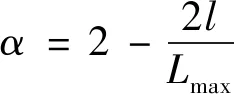
(12)

X(l+1)=|Y-X(l)|ebu(cos2πu)+Y(l)

(13)

式中：Lmax为最大迭代次数；Y为当前最优位置；b为螺旋形式系数；u为[-1，1]之间的随机数．

3)搜索猎物：座头鲸进行搜索猎物时是根据各鲸鱼彼此的位置进行随机搜索，其计算公式为

D=|C*Xrand(l)-X(l)|

(14)

X(l+1)=Xrand(l)-A*D*

(15)

式中：Xrand(l)为随机选中的鲸鱼个体位置向量．

2.3 改进WOA算法

虽然WOA算法是一种新型的启发式算法，但传统WOA算法仍然存在陷入局部最优的缺陷．本文通过使用混沌映射、自适应收敛因子和引入自适应权重的方式对WOA算法进行改进．

1)混沌映射：使用混沌映射对种群初始化可以提高初始种群的多样性，提高WOA的搜索精度，本文使用sine映射对种群进行初始化，其计算公式为

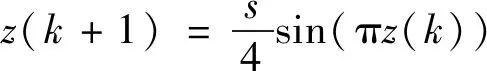
(16)

式中：s为[0，4]之间的常系数．

2)自适应收敛因子和自适应权重：在算法前期，搜索空间大，需要加快搜索速度，后期接近目标，需要缩短步长，以免陷入局部最优．传统WOA算法的收敛因子是线性递减的，使得算法容易陷入局部最优．本文将收敛因子改进为非线性递减形式，同时引入自适应权重，使得前期搜索收敛因子和步长较大且缓慢减小，避免算法过早陷入局部最优，后期收敛因子和步长较小且迅速下降，提高局部搜索能力．自适应收敛因子α和自适应权重v计算公式为

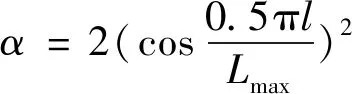
(17)

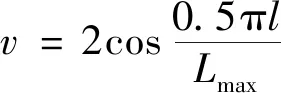
(18)

引入自适应权重后的鲸鱼位置更新计算公式为

X(l+1)=vY(l)-A*D*

(19)

2.4 水电机组故障率预测模型

将水电机组役龄、检修类型、检修次数和水电机组健康状态得分作为输入，对改进WOA-BP神经网络模型进行训练，完成模型训练过程后，使用输入数据通过已训练完成的模型对水电机组故障率进行预测．基于改进WOA-BP神经网络的水电机组故障率预测模型流程如图3所示．

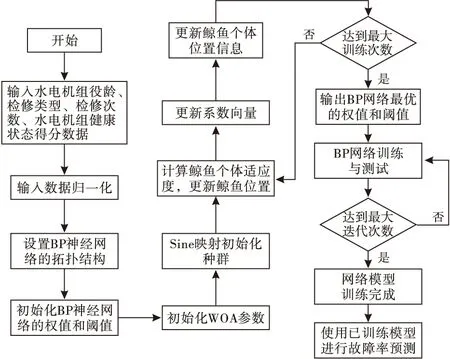
图3 水电机组故障率预测流程图

3 基于改进WOA-BP神经网络的水电机组ADC效能评估模型

结合ADC模型和水电机组故障率模型，考虑检修和检修疲劳的影响，从可用性、可靠性和固有能力3个方面对水电机组进行效能评估．基于改进WOA-BP神经网络的水电机组ADC效能评估模型如图4所示．该模型通过水电机组故障及检修的历史数据，使用改进WOA-BP神经网络对水电机组故障率进行拟合预测，结合ADC模型，对水电机组效能进行计算，最后在时间尺度下输出水电机组变化曲线．

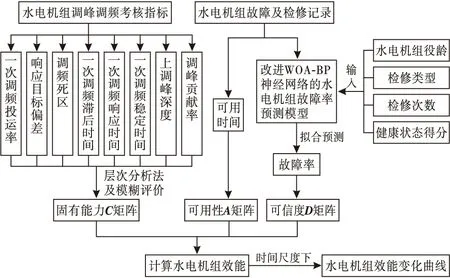
图4 基于改进WOA-BP神经网络的水电机组效能评估模型

4 算例分析

4.1 参数设置

本文算例将改进鲸鱼优化算法的初始种群规模设置为30，迭代次数为50．选择tansig和purelin分别作为BP神经网络的隐层激活函数和输出激活函数，设置BP网络学习速率为0.01，训练误差为10-5，训练次数为1 000次．隐含层的节点数根据经验公式进行选择，计算公式为

(20)

式中：N为隐含层的节点数目；n为输入节点数目；m为输出节点数目；p为[1，10]之间的常数，本文选取p=10．

4.2 水电机组故障率拟合预测

为检验水电机组故障率拟合预测精准度，使用标准BP神经网络、GA-BP神经网络和WOA-BP神经网络3种方式与改进WOA-BP神经网络进行对照．采用均方根误差、平均绝对误差和平均绝对百分比误差作为各方法的准确性指标，其计算公式分别为

(21)

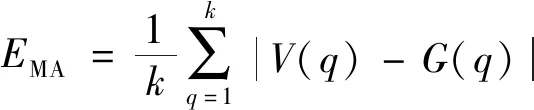
(22)

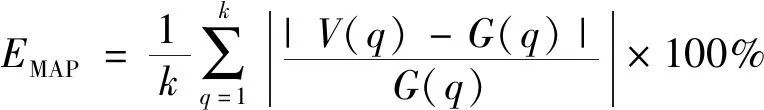
(23)

式中：ERMS为均方根误差；EMA为平均绝对误差；EMAP为平均绝对百分比误差；k为测试样本数量；V(q)为模型预测值；G(q)为水电机组故障率真实值．

根据某地水电站2号机组2009—2021年65组历史统计数据，以时间顺序选择前50组数据作为训练样本，后15组作为测试样本，使用4种方法对水电机组故障率进行预测，通过准确度指标比较各个方法的准确性．各方法训练结果如图5～6所示．

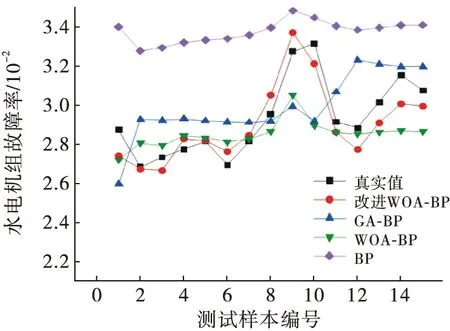
图5 各方法对水电机组故障率数据训练结果

图6 各方法训练结果的相对误差

各方法的相对误差及准确度评价指标数据见表2～3．

表2 各方法预测数据的相对误差(×10-3)

表3 各方法的准确性指标数据

如图5～6所示，改进WOA-BP神经网络相较于其他3种方法，对于水电机组故障率的预测效果更好．从表3可知，改进WOA-BP神经网络的EMA、EMAP、ERMS分别为7.753×10-4、2.654%和8.745×10-4，其准确度指标值均小于其他3种方法，预测精度更接近于水电机组真实故障率．

4.3 水电机组效能计算

以某地水电站2号机组2014年为例，进行单一时间点下的水电机组效能计算．

1)可用性矩阵计算

根据式(3)～(4)对可用性矩阵的元素进行计算，得到2014年水电机组相应的可用性矩阵

A=[0.978 0.022]

2)可信度矩阵计算

将检修类型分为不检修、小修和大修，并分别使用0、1、2表示．根据改进WOA-BP神经网络，输入水电机组役龄、检修类型、检修次数和水电机组健康状态得分数值，分别为5、0、3、88，训练得到水电机组故障率λ=0.026 56.

根据式(6)可得

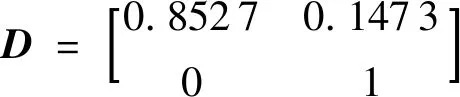
3)固有能力矩阵计算

根据层次分析法，对一次调频投运率、响应目标偏差、调频死区、一次调频响应上升时间、一次调频响应滞后时间、一次调频稳定时间、上调峰深度和调峰贡献率8个指标赋权，得到权重矩阵

w=[0.034 6 0.053 6 0.081 2 0.114 0

0.160 2 0.235 7 0.160 2 0.160 2]

根据模糊评价方法，对指标归一化数据进行处理得到隶属度矩阵

R=

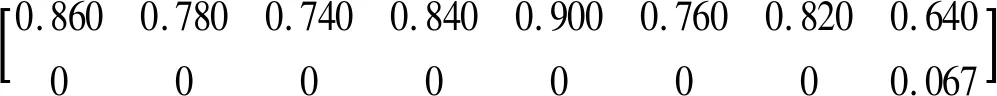
由式(7)计算固有能力矩阵

C=[0.802 4 0.002 3]

由式(1)计算2014年水电机组效能值E=0.669 5.

4.4 水电机组效能曲线

根据某地水电站2号机组2011—2021年总共11年运行考核数据，使用4种方法分别以年为时间单位对水电机组效能进行计算．图7是水电机组效能变化曲线图．

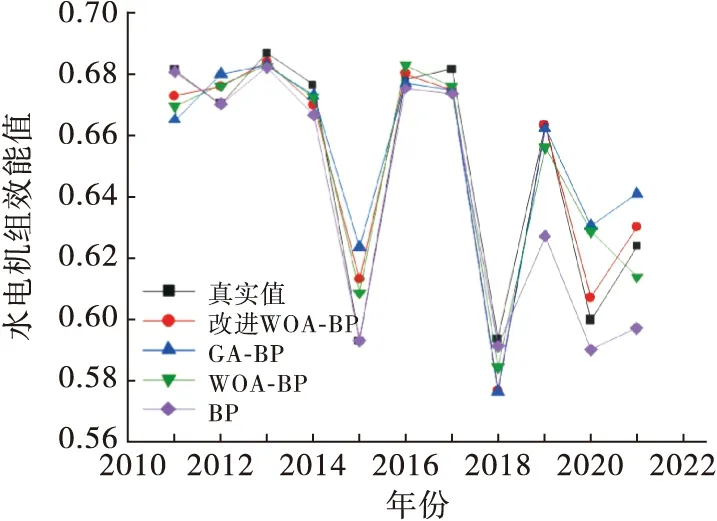
图7 水电机组效能变化曲线

基于改进WOA-BP神经网络的水电机组效能评估模型对比其他3种方法其准确性更高，各方法的计算准确度见表4．

表4 各方法的效能计算准确性指标数据

水电机组的效能值越高，反映了水电机组的可靠性越高，工作性能越强，任务完成效果越好．根据图7，该水电机组效能值随着设备役龄的增长总体呈现下降趋势，在2013、2016、2019、2021年分别安排了机组检修，使得水电机组效能获得提升．该水电机组2011—2021年的效能值在[0.55，0.70]之间波动，效能低于0.62时说明该机组运行状态较差，可以设置0.62为警告值，当效能值低于0.62时可以考虑安排机组检修来提升水电机组效能．

5 结 论

针对水电机组效能评估问题，本文提出基于改进WOA-BP神经网络的水电机组ADC效能评估模型，研究得到如下结论：

1)对水电机组使用ADC方法，从可用性、可信度和固有能力3个方面建立全面科学的水电机组效能评估体系，解决了传统可靠性评估不够全面的问题．

2)对水电机组历史数据使用改进WOA-BP方法进行故障率拟合预测，并与BP、GA-BP、WOA-BP这3种方法进行比较，验证了改进WOA-BP方法对水电机组故障率有更高的拟合预测准确性．

3)基于改进WOA-BP神经网络的水电机组ADC效能评估模型可准确量化水电机组在不同时间下的效能变化，可为水电机组管理和检修提供指导作用．