无人驾驶路径规划算法综述
海振洋,王健,牟思凯,杜若飞,费明哲,李晶玮
(250399 山东省 济南市 山东交通学院)
0 引言
自动驾驶技术作为智能交通中重要的一个环节,已经成为汽车工业发展过程中的新兴趋势。2020 年11 月,李克强教授在2020 世界智能网联汽车大会上公布了《智能网联汽车技术路线图2.0》[1],该文件为汽车产业未来15 年的发展设定了技术路线,中国智能网联汽车的技术架构和关键技术已经形成了三横两纵的格局,智能决策技术是三横中的核心之一。行业研究和学术界之所以青睐它,是因为它可以充分利用资源,改善驾驶环境,减少道路拥堵。算法策略使硬件发挥出充分的效能,实现多功能控制,负责逻辑制定的规划算法在控制中占据重要地位[2]。运动规划的方法是通过规划路径,躲避障碍物,优化路线,使车辆精准、快捷地抵达目的地,提高了司机的工作效率,增加了安全性。
本文阐述了自动驾驶汽车路径规划的各种方法,深入分析路规划算法的属性。从时间处理的复杂程度(算法运行过程所需要的工作量)、空间处理的复杂度(算法在计算过程中会占用的内存空间量)和规划准确度来剖析算法的局限性、可行性。同时,对这些算法的改进方案、方式进行归纳总结,提出算法研究方式、方向以及优化算法的可能性。
1 路径规划算法介绍
规划是对未来时域、空域中车辆一系列行为方式的计划。从涉及的时空大小可以分为局部(微观)路径规划和全局(宏观)路径规划。局部路径规划也称动态路径规划,是根据环境感知的信息,实时改变行驶状态,包括换道,避障等。全局路径规划也称静态路径规划,根据当前定位在已知的地图上规划一条到目标位置的路径。
路径规划一般分为3 步:(1)建立环境模型:根据现实的道路情况,建立一个抽象的环境模型,为算法策略提供地图模型,便于计算机进行路径规划;(2)搜索路径:根据算法策略在抽象的环境模型上规划一条从初始点到目标位置的路径,尽可能找到一条最优路径;(3)路径处理:对规划出的路径进行优化,删除冗余节点,改善平滑度。
1.1 全局路径规划
1.1.1 Dijkstra 算法
Dijkstra 算法[3]是1959 年狄克斯特拉提出的一种遍历各个节点的最短路径算法,它能够高效解决小范围内最短路径问题。Dijkstra 算法采用广度优先思想和贪婪搜索策略,通过一个数组集合存储从起点到每个节点的最短距离,并处理最短路径点进行保存,一边进行数据处理,一边进行数据分类,解决无向图或加权有向图的单源最短路径问题。算法步骤如下:
第1步:根据如图1所示路径节点,设起始点A,把路径节点做上标记如表1 所示,每一节点临近节点如表2 所示,设置两个数组集合S 和U。S 代表每个节点到起点的最短距离数据集合,U 表示未经过数据处理的节点集合。最短路径min[i,j]为距离起点最短的点(i 为S 数组中节点,j 为U 数组中节点)。初始时,S 集合内只有节点A;U 集合中有除S集合外的其他节点。出发点设置为S={A(0)},U={B(min[A,B],C(min[A,C]),D(∞),E(∞),F(∞)}。

表1 字母-数字节点对应表Tab.1 Correspondence of alpha-numeric nodes

表2 节点临近节点表Tab.2 Adjacent nodes

图1 路径节点Fig.1 Path nodes
第2 步:在U 集合中选取下一个相邻节点,计算所选中节点离起点最短距离min(A,j)。
第3 步:计算起点A 到U 中每个节点的距离。更新当前U 中节点的距离,由第2 步中确定了的min(A,j)求出最短路径的节点,利用min(A,j)来计算其它节点的距离;例如,min(A,j)的距离可能大于min(A,i)+min(i,j)的距离。
第4 步:重复第2 步和第3 步,直至终点,算法结束。S 集合中的结果就是最短路径。
Dijkstra 算法优缺点:由于Dijkstra 算法遍历了全部节点,因此得到的最短路径准确度好,成功率较高,且鲁棒性较好。但在实际应用于复杂的大范围路径拓扑网络时,时间、空间处理复杂度高,导致效率低下,消耗的时间长,内存消耗大;其次,算法忽略了交通网络中的冲突、拥挤等因素。
梁彧[4]在传统算法基础上引入了对路径代价进行估计的估价函数,改善了Dijkstra 算法的空间复杂程度,提高了路径规划的效率。
1.1.2 A*算法
A*算法[5]是一种图搜索法,它在经典Dijkstra算法中加入了启发式函数和估价函数进行约束,估价函数作为核心部分之一可以根据环境信息进行调整,在静态路网搜索中效果显著,估价函数如下:
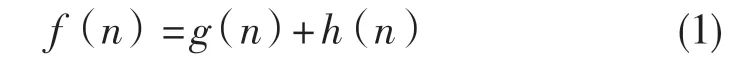
式中:g(n)——从初始状态到当前状态n 的实际代价;h(n)——从当前状态 n 到目标状态的估计代价;f(n)——从初始状态通过当前状态n 到目标状态的总代价估计。
若采用曼哈顿距离作为启发函数:

式中:xd——目标位置的横坐标;yd——目标位置的纵坐标;xn——节点n 的横坐标;yn——节点n的纵坐标。
估价函数h(n)作为A*算法中的核心,能够决定A*算法的时间、空间复杂程度。在估价函数中,若h(n)与节点n 运动到目标节点的实际代价相等,算法能够在最短时间内找到一条有效路径;若h(n)比从节点n 运动到目标节点的实际代价小,不仅内存消耗增加,路径中的冗余节点也会增加;如果 h(n)比节点n 运动到目标节点的实际代价大,虽然消耗的时间短,但是对A*准确度影响较大[6-7]。
A*算法具体步骤如下:
第1 步:对初始点和目标点初始化,设置open 和close 两个集合。open 集合为待分析节点数据集合,close 为已经处理过的数据集合。初始后,把初始位置作为父节点,放入close 集合中,初始位置周围8 个节点设为子节点,放到open 中;
第2 步:根据估价函数式1,处理8 个节点,可以横向、纵向、斜向移动,选择最小节点放入close 中,把 最小的节点设为新的父节点。若新父节点相邻节点已经在open 中,处理生成最佳路径,更新open 和close 集合;
第3 步:循环前两步,直到找到目标点为止。
A*算法存在规划路径转折点多、冗余节点多、转折角度过大且距离障碍物过近等问题,使算法控制效率降低,时间、空间复杂程度高,在大型地图环境效率低。周克帅[8]等对A*算法和人工势场算法进行改进,并把两种算法融合,仿真结果不仅在静态环境下可以快速规划出一条最优路径,而且在复杂的动态环境下也可以实时躲避障碍物。
1.1.3 蚁群算法
蚁群算法是1991 年Dorigo[9]等根据模仿蚂蚁寻找食物的方式提出的一种仿生算法。蚂蚁寻找食物时会释放信息素在经过的道路上,蚂蚁之间可以相互感知信息素。信息素浓度随时间而降低,当蚂蚁遇到岔路时,通常会选择信息素浓度高的路径通过,与此同时,会释放自己的信息素标记这条路径上,使信息素浓度増加,大量蚂蚁通过后,在正反馈的作用下,蚂蚊会找到条最短路径。
设蚂蚁总数量m,节点数量n,节点i、j 之间距离表示为(i,j=1,2,…,n),设时间为t 时,节点i、j 之间道路上信息素浓度为τij(t)。初始时,设整个路网信息素浓度相同,设τi(jt)=τ0。第k 只蚂蚁(k=1,2,…,m)选择下一个目标节点时,依据路径上的信息浓度来判断,设(t)为t 时刻第k 只蚂蚁从节点i 运动到节点j 的概率,如式(3):

式中:τij——路网上信息素浓度;α——信息素重要因子;β——启发函数因子;p——信息素挥发因子;Lk——在当前遍历中最优路径;Q——总信息素量。
式(3)中,设τij(t)为启发函数,是蚂蚁从节点i 运动到节点j 的期望值,有。
当蚂蚁完成第1 次遍历时,更新各个路网上的信息素浓度。

蚁群算法在路径规划中具有正反馈、强鲁棒性和较好适应性的特点,但收敛速度慢,时间复杂程度高,易陷入局部收敛,内存消耗大,准确率不高[10]。何雅颖[11]等通过局部分块优化策略分别优化各子区域,改良信息素的变化过程,不仅避免陷入局部最优,而且使算法收敛速度有所提高。
1.1.4 RRT算法
Rapidly-Exploring Random Tree 是Lavalle[12]在1998 年提出的一种基于采样的快速扩展随机树算法。采样算法适用于普遍动态模型,算法的增量特性使其更易于实现动态实时。RRT 算法是从初始位置出发后一边搜索拓展一边建图。快速扩展随机树在每次迭代更新中随机选择新的配置顶点,拓展路径结构,直到抵达目的地为止。算法步骤如下:
第1 步:初始化后,定义qinit为初始点,定义qrand为采样点,qrand为状态空间中随机一点;
第2 步:以qinit到qrand方向为树枝延伸方向,拓展函数从起点出发向qrand方向扩展一段距离,设新到达的节点为qnew;若qnew1向qrand生长时经过障碍物,放弃此次生长,若qnew1向qrand生长时未经过障碍物,此路径有效;
第3 步:重复第2 步,直到qnew和目标点距离小于既定值,路径规划成功。为了使算法尽可能满足需要,可设定生长次数上限。如果在生长次数限制内无法规划出一条完整的路径,则此次规划失败。
RRT 算法在运行过程中不需要根据周围环境建立模型,算法简明,结构简单,对高维度空间的问题和一些复杂环境有很好的适用性,对未知空间的快速探索强,但是算法搜索具有盲目性,对附近障碍物距离强烈依赖,空间复杂程度高。户望力[13]通过对扩展节点拓展方式进行改良,使得车辆进行路径规划时更加具有方向性,能够实现在复杂环境下也具有较好的适用性,算法的精确度有了较大改善,减少了时间复杂程度。
1.2 局部路径规划
1.2.1 模拟退火算法
模拟退火算法是1953 年Metropolis 等根据固体退火的过程提出的一种近似求解算法[14],在大范围的复杂环境优化问题中有很强的适用性。在一般组合的优化问题加入概率突跳特性。概率突跳特性可以使得局部最优解能概率性地跳出,导致得到的解概率性是全局最优。模拟退火的过程如下:
在一定初始温度和初始解的情况下,随着温度的降低,每个温度状态下的转变会产生一个新的解。如果当前解小于上一次迭代生成的解,则接受当前解决方案,否则概率性接受新方案。经过多次迭代可以得到最优解。当固体从状态i 经过降温变化到状态 j,它所具有的能量从E(i)变化到E(j)。显然,如果E(j)<E(i),接受新的状态 j,否则依据概率性P,决定能否接受新解。

式中:T——固体的温度;K——玻尔兹曼常数。
x 表示温度T 下的一个解,通过退火,可以生成一个新解x',那么接受x'的概率为

模拟退火算法可以有效地求解多项式复杂程度的非确定性问题,但是也存在如下问题:
(1)模拟退火算法性能在全局搜索中会被温度T 的初始值设置影响;
(2)同一温度下会产生大量的搜索,使得时间、空间复杂程度增加。循环次数使得内存消耗大;
(3)温度管理问题也会影响算法的性能[15]。袁佳泉[16]融合模拟退火与蚁群2 种算法,利用2种算法设置双层启发式函数求最优解,退火机制的概率突跳特性有效避免蚁群算法陷入局部最优,既提高了全局搜索性能,也降低了时间复杂程度。
1.2.2 动态窗口算法
动态窗口算法是由Dieter Fox[17]等于1997 年基于曲率速度思想提出的一种局部路径规划方法,考虑到运动速度、载体的运动方向和到最近障碍物的距离3 个方面,通过离散搜索空间进行优化。
DWA 算法要将位置控制转化为速度控制,因此需要对车辆的运动模型进行分析。设vx为车辆在x 轴上的速度,vy为车辆在y 轴上的速度,θt为车辆当前朝向角,θt+Δt为Δt 时间后车辆朝向角,ω为车辆当前角度。在采样周期t 内,(xt,yt)为车辆当前位置坐标,Δ t 为时间间隔;(xt+Δt,yt+Δt)为Δt 时间后车辆位置坐标。其运动模型如下:

车辆受自身结构限制,速度有最小值和最大值的约束。设Vm为小车最低速度和最高速度之间的速度集合,小车速度为(v,w),则Vm的取值为

因为电机力矩受到最大加速度和最大减速度的限制,所以在车辆轨迹前向模拟的周期内,存在一个动态窗口,该窗口的速度集合是小车在下一个时间间隔内实际能够达到的速度。设t 为加速度v'和角加速度ω'作用的时间,Vc为车辆当前速度,ωc为车辆当前角速度,(vc,ωc)则为小车的实际速度,则动态窗口Vd定义为

为了防止小车与障碍物发生碰撞,需要在最大减速度条件下对小车的速度进行约束。设小车速度为(v,ω),则允许速度集合Va定义为

式中:dist(v,m)——速度对应的轨迹,也就是一段圆弧上,离障碍物的最短距离;vb'和ωb'为制动加速度。对速度的采样搜索空间施加约束后,可以得到在动态窗口内区域Vr,因此Vr可以定义为这些限制条件的交集,表示为

动态窗口法评价函数:DWA 算法可以根据速度采样后的结果推演出不同的轨迹,再运用评价函数对轨迹和速度进行评价,通过评价函数选出的避障速度能够保证车辆避开静态障碍物。设评价函数G(v,w),可以通过式(14)计算:

式中:方位角heading(v,ω)——小车方向与目标方向的精确程度的指标;dis(tv,ω)——小车沿着当前路径运动时到最近障碍物的距离;vel(v,ω)——评估小车在当前位置的速度及其进展过程。
DWA 算法有2 点不足:
(1)只有一个目标点,缺少中间指引在大范围的复杂环境中概率性得到最优路径;
(2)未将已知障碍物和未知障碍物区分,遇到动态障碍物难以避障。
刘建娟[18]等融合动态窗口法与A*算法,量化环境中的障碍物信息,根据障碍物信息调节A*算法启发函数,根据弗洛伊德算法思想改良路网节点算法,最终使得融合算法更加平滑,减少了转折节点,删除冗余节点,在复杂的环境中也保证了计算出最优路径的情况下,可以做到实时避障。
1.2.3 人工势场法
人工势场法是1985 年Khatib 博士提出一种抽象的虚拟力场法[19],该算法是把汽车在现实环境中的运动抽象成为一种在力场中的运动。目标位置对于车辆相当于引力势场,离目标点距离越远引力势能越强。障碍物对于车辆相当于斥力势场,车辆离障碍物越远斥力越小,通过引力场与斥力场的合力可实现同步规划路径和轨迹平滑度的处理,根据搜索势函数的下降方向可以规划出一条最佳路径。
设小车在空间位置为X=[x y]T,目标位置为Xg=[xgyg]T,引力场增益为k,则小车在X 点受引力场函数Uatt(X)为;

相应的引力场负梯度Fat(tX)为;
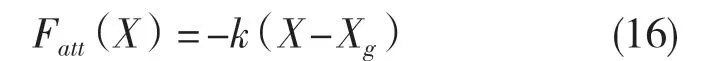
设η为斥力场增益常量,λ为小车到最近障碍物的距离,λ0为障碍物影响的最短距离,斥力势场函数如式(17),斥力势场函数的负梯度为式(18),汽车所受合力F(x)为
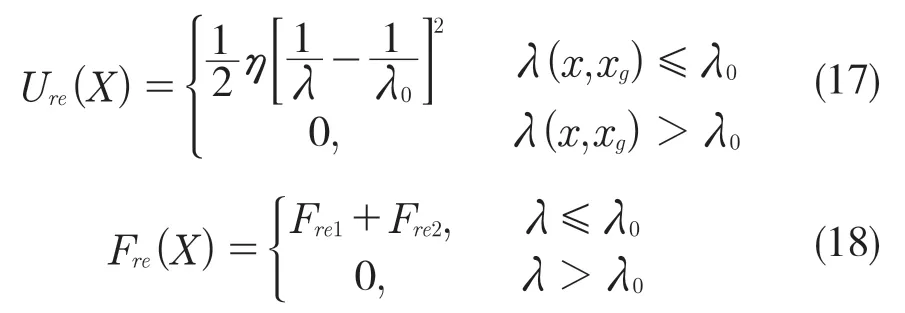

人工势场法算法简明,时间复杂程度低,准确度高,能够实时控制车辆行驶状态,且所规划路线较为平滑,受到大量的使用与改进。但是当处于多障碍物的复杂环境时,车辆受到的引力与斥力的合力可能为0,导致车辆停止前进,陷入局部最小值。有时候会规划道路失败。张珂[20]等基于传统人工势场算法改善了障碍物势场力设置中的不合理以及道路边界定义模糊的问题,仿真结果在综合性能上比传统算法平顺。
2 展望
经过多年的实践和应用,路径规划算法在不同学科、不同领域的相互融合中逐渐成熟,以下是对算法优化的可行性方案总结和展望。
(1)对于经典路径规划本身的优化,每一种算法在实践过程中都会表现出自身的局限性,可以针对对应的局限性加约束条件优化结果,也可以加入强化学习方法,从基于值和基于策略两类改进常规路径规划,增强环境适应性;
(2)对于路径规划融合算法,面对复杂的交通环境时,任何一种路径规划算法都不可能处理一切路径规划问题。加上开发新算法的难度太大,且不一定能够比传统算法表现更优秀。路径规划算法之间的性能互补为解决此问题提供了可能。如A*与DWA 算法融合[21]。
(3)路径规划算法和环境建模的融合是跨学科处理复杂问题的方法。在动态环境中,三维连续动态环境信息的多变性,使得算法本身难以做到有效的应对,适合的建模技术和与之适应的路径规划算法相结合可以使结果更加平滑、高效,增加了求解的准确度。如蚁群算法和栅格法的联合[22]。
(4)对于基于Vehicle to X 的路径规划算法设计,随着科学技术应用的拓展,多种交通设备相互协作变得越加默契,在应用中得到很好的实践。这使得路径规划算法设计能有新的拓展方向。
3 结语
路径规划算法作为无人驾驶任务决策的核心,吸引着各研究人员进行探索,逐渐形成百家争鸣的景象。本文通过分析经典路径规划算法的方法和性能,从时间复杂程度、空间复杂程度以及准确度方面进行讨论;其次,分析各个算法优化的方式,优化后算法的可行性、拓展性;最后,依据改良方式以及学科领域的拓展,对无人驾驶路径规划的发展前景做出了一个符合实际的展望。
——以中国、新加坡教材的三角形问题为例

