基于FPGA的裁切机步进电机控制算法设计

王 庆，周 锋，郭乃宏，孔祥晔，王如刚

(1.盐城工学院 信息工程学院，江苏 盐城 224051;2.盐城雄鹰精密机械有限公司，江苏 盐城 224006)

0 引言

随着科学技术的飞速发展，步进电机因其精度高，响应快，误差小等优点，所以在运动控制领域的应用十分广泛，同时对其运动控制系统的要求越来越高。步进电机加减速控制是运动控制系统中的重要组成部分。在裁切机的加工中，对进给、启停或轨迹转换等一系列的刀具运动进行加减速控制，能够提高加工效率和裁切精度。步进电机加减速常用的控制器有可编程逻辑控制器(PLC，programmable logic controller)、单片机[1-2]和现场可编程门阵列(FPGA，field programmable gate array)。但是，PLC和单片机的控制方法，不仅操作繁琐，还会影响实际工作效率。FPGA具有并行处理，丰富的逻辑资源，在设计过程中可以根据实际的工作需求进行灵活更改。而研究人员发现FPGA可以对步进电机进行高效的控制，能够实现步进电机的启停和加减速。近些年，许多学者对用FPGA控制步进电机做了一系列研究[3-9]。刘鹏[3]提出了以FPGA和STM32单片机相结合的算法，实现了灵活的梯形加减速算法，但是研发成本高以及逻辑资源占用多。胡承祖[4]提出了基于FPGA采用查表法实现了梯形加减速算法，虽然减少了成本和资源占用，但是降低了灵活性。邱静超[5]等人实现了传统的梯形加减速算法，但需要计算每个阶段的时间才能使步进电机达到最终位置，灵活性不高。桑彭[6]等人提出了基于FPGA的S型曲线加减速算法，解决了梯形算法中不平稳和不连续的现象，但是计算量大，实现困难，采用查表法实现，当步进电机位置改变时，需要重新设计速度表，操作较为繁琐。因此，本文提出了一种基于FPGA实现步进电机的加减速控制，对比分析梯形加减速算法，指数加减速算法和S型加减速算法，选择梯形加减速算法并对算法做出改进，用时间来确定减速点，并且算法能够自动计算出减速点的位置。在保证精度和可靠性的前提下，能够提高灵活性，使减速点的确定具有的自适应能力。

1 步进电机的工作原理

步进电机[10]是一种将脉冲信号转换成角位移或线位移的开环控制元电动机。当输入一个脉冲信号给步进电机，转子就会转动一个角度或者是前进一步，这个角度简称为步距角。步距角和输入的脉冲数成正比，转速与脉冲频率成正比。因此，只需控制脉冲频率就可以控制步进电机的运动快慢。

步进电机按结构可以分为反应式步进电机、永磁式步进电机、混合式步进电机等，其中最广泛使用的是两相混合式步进电机，主要是由定子铁芯、定子组件、转子铁芯组成。步进电机的基本参数有空载启动频率、步距角和精度。其中步距角表示每个脉冲对应步进电机走一步所需要旋转的角度，由公式(1)确定。

B=360°/ZKm

(1)

其中:B为步距角；Z为转子齿数，K为通电系数；m为定子绕组相数。

本文使用的步进电机为两相混合式42步进电机，步距角为1.8°，即步进电机转一圈需要200个脉冲。

2 算法分析

2.1 加减速算法的分析

加减速控制是根据给定的步进电机目标位置、初始速度、最大速度和加速度等数据来计算出当前时间的速度值。常见的加减速算法有S型加减速[11-12]、指数加减速[13]和梯形加减速[14]等算法。

如图1所示，S型加减速运动常用来解决运动控制中加速度突变的现象。S型曲线并不是一种固定的算法，一般分为7个部分，包括加加速阶段、匀加速阶段、减加速阶段、匀速阶段、加减速阶段、匀减速阶段和减减速阶段。S型曲线的核心思想是让加速度不产生突变，其加速平稳，柔性快速，。但是由于涉及阶段较多，算法复杂，实现难度高。现阶段的S型曲线多采用查表法，即事先规划好速度数曲线，再将对应的曲线生成速度数据表放入ROM核中，再根据要求从ROM中读取速度数据表。这种方式不仅操作繁琐，而且灵活性低。

图1 S型曲线加减速

如图2所示，指数加减速运动，就是在加速阶段和减速阶段的曲线变化成指数函数。

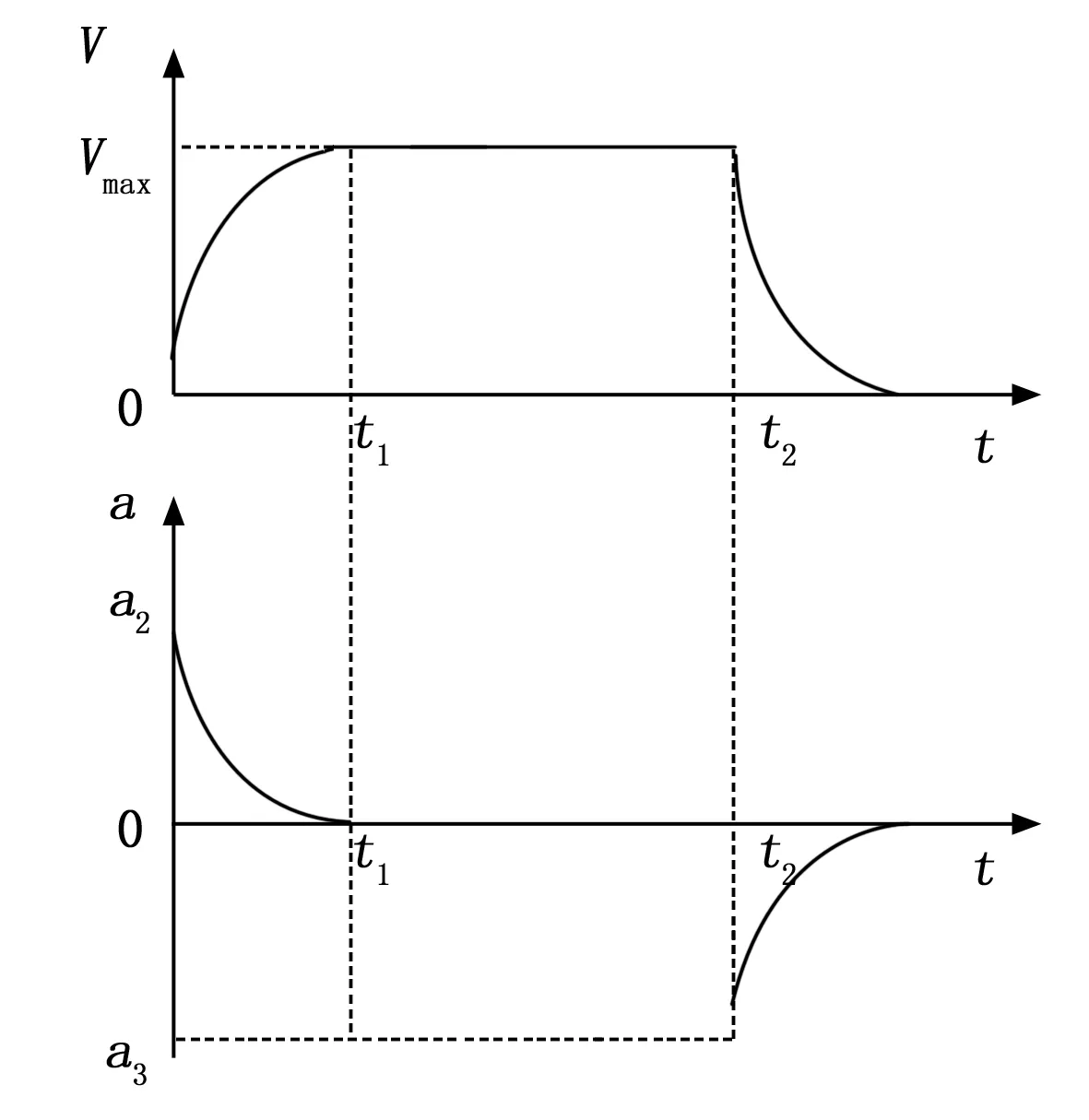
图2 指数函数加减速

指数加减速运动在起始速度时，它的加速度是最大的，随后不断衰减，在进入匀速运动时的加速度最小，匀速运动时候的加速度为0，并保持最大速度。随后进入减速阶段，在减速阶段中，速度以最大的加速度减速，随后加速度不断衰减至最小，当速度为0时，运动停止。指数加减速的特点是速度平稳，运动精度较高，但是初始速度高，容易引起步进电机的冲击，在加减速的起点存在加减速突变的现象，限制了加速度的提高。

梯形加减速原理：运动开始后，在加速阶段以恒定的加速度加速至最大速度，在匀速阶段以恒定的速度保持不变，在减速阶段以恒定的加速度减速至最低速度。其速度曲线和加速度曲线如图3所示。

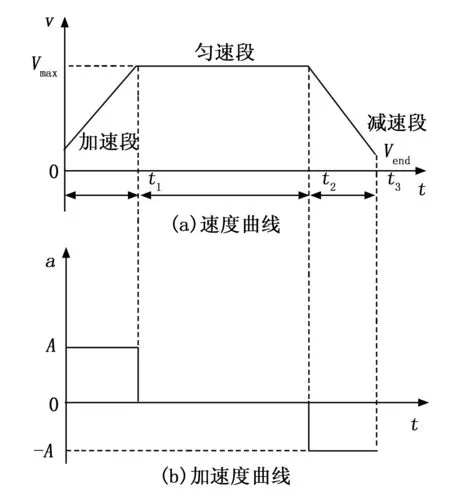
图3 速度曲线和加速度曲线

梯形加减速曲线算法简单方便，占用时间少，响应快，实现简单，但是在加速阶段和减速阶段容易产生速度突变。适用于频繁启停和速度变化范围大的场合。梯形加减速控制可以分为3个阶段：

1)加速阶段。如果当前速度小于最大速度时，就会以某一恒定不变的加速度A加速，直至到达最大速度Vmax为止。

2)匀速阶段。步进电机会保持最大速度Vmax不变，此时加速度A的值为0。

3)减速阶段。加速度为-A，与加速阶段的加速度大小相等，方向相反，直到减速至Vend停止运动。

综上所述，针对裁切机工作时需要频繁启停的特性，梯形加减速算法相对于其它两种算法可靠性高，实现简单。但是传统的加减速算法采用ROM查表法，该方法虽然实现简单，但是需要先规划好速度数据表，当步进电机位置改变后需要重新规划速度表，操作繁琐，不利于实际应用。或者通过计算每个阶段的运动时间的方法来实现梯形加减速，该法在计算上比较复杂。

由图3可知，路程等于时间乘速度，因此步进电机的最终位置为速度曲线的面积。每个阶段面积由公式(2)确定：

(2)

其中:k为加速度A；S1为加速阶段的面积；S2为匀速阶段的面积；S3为减速阶段的面积。

梯形加减速曲线与坐标轴的面积可由公式(3)确定：

S=S1+S2+S3

(3)

其中:S为梯形加减速曲线的面积。

但是，该方法在计算上比较复杂，在知道步进电机的目标位置后，需要计算出每个阶段的运动时间，操作繁琐，在实际应用中会降低工作效率。

2.2 改进后的梯形加减速算法

针对上述传统的梯形加减速的缺点，通过对减速点的确定改进梯形加减速算法。本文设计的梯形加减速算法的减速点是通过步进电机运动的时间来确定的。改进后的加减速图如图4所示。

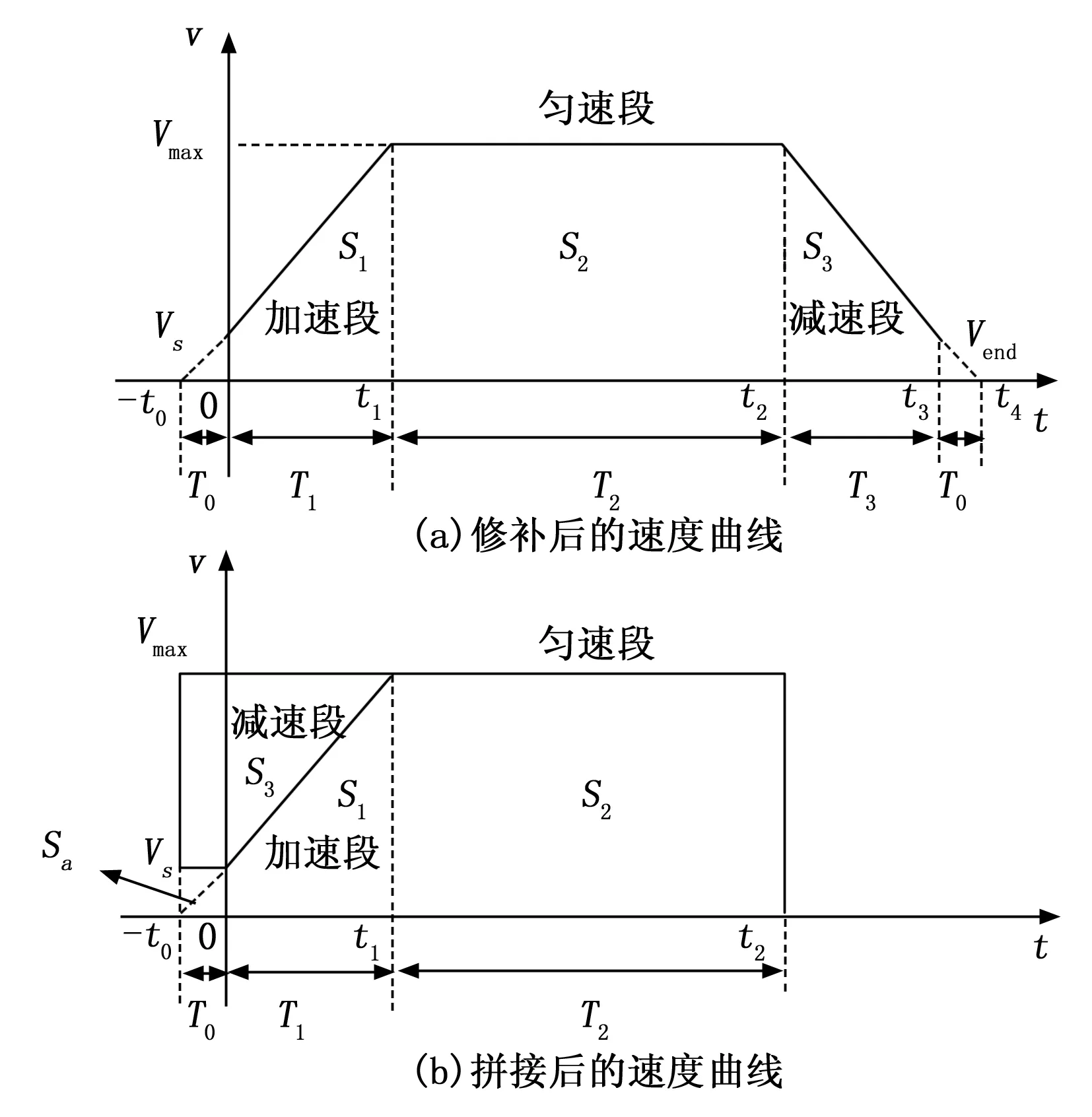
图4 改进后的速度曲线图

为了便于确定减速点，需要将减速阶段的面积S3剪切到加速阶段的面积S1处。但是步进电机有一个启动频率的概念，因此，起始速度Vs不为0，这就导致将速度曲线分割后，把减速阶段的面积拼凑到加速阶段无法成为一个完整的矩形，会缺少一块面积Sa。这样就无法计算出减速点的时间。所以，需要对速度曲线修补，修补后的图形为一个初始速度从0开始的等腰直角梯形。如图4(a)所示，将减速阶段的面积拼接到加速阶段，如图4(b)所示，拼接后的速度曲线为矩形。矩形的面积是由原先速度曲线面积图和修补的面积相加得来的。新矩形的长由两部分组成，分别为加速阶段的时间与匀速阶段的时间。修补的面积可以由公式(4)确定：

Sa=VSt0

(4)

其中:t0可由公式k(-t0)+VS=0求出。且t0只与起始速度Vs和加速度A有关。因此矩形的面积可以根据公式(5)得出：

Sn=Sa+S

(5)

其中:Sn为拼接后的速度曲线面积,S为梯形加减速曲线的面积。

根据公式(6)求出减速点的时间：

t2=Sn/Vmax-t0

(6)

这样，无论步进电机的目标位置如何改变，该算法能够自动确定减速点，从而确定步进电机每个阶段的运动时间。相比于通过计算剩余减速距离的方法确定减速点，该算法确定减速点的过程简单。

3 系统设计

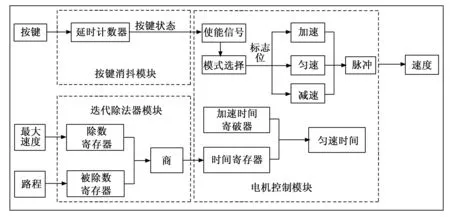
图5 系统设计框图

本文设计的控制系统由FPGA、步进电机驱动器和步进电机本体三部分组成[15-16]。其系统设计框图如图5所示。当按键按下时，按键消抖模块首先会判断按键是否按下，如果按下，会给步进电机模块一个使能信号，步进电机模块会根据标志位的状态选择运动模式，然后输出脉冲。同时，迭代除法器模块会根据最大速度和路程，计算出减速点的时间，送给步进电机模块，步进电机模块会根据减速点的时间给每个运动模式分配运动时间。

3.1 加减速控制硬件设计

FPGA选用Xilinx公司的A7系列，芯片型号为XC7A35TFGG484I-2，利用串口通信将上位机的命令传递给FPGA，FPGA通过步进电机电机驱动器DM422驱动步进电机，从而控制步进电机的转动。DM422两相步进电机驱动器是基于PI电流控制算法设计的高性价比细分型驱动器，低噪音，低振动。FPGA与DM422之间通过数字IO接口对步进电机驱动控制。驱动器用于将FPGA发送给步进电机的电脉冲信号转换为角位移量。本文使用的是42CM04型号步进电机，FPGA与驱动器DM422的数字IO接口连线如图6所示。

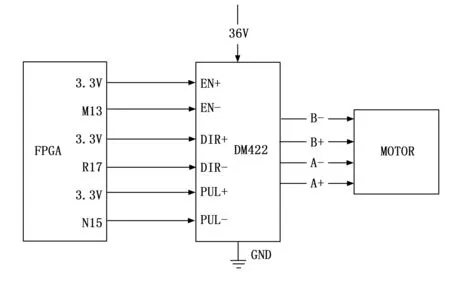
图6 FPGA与DM422的数字IO接口

其中，EN是步进电机的工作使能信号,该信号拉低时，DM422为使能状态，电机正常运转；EN信号为高电平时，DM422功率部分关断，电机无励磁。DIR是步进电机方向控制信号，当信号拉高时，则会使步进电机正转；当信号拉低时，则会使步进电机反转。PUL是驱动步进电机的脉冲信号。该信号的上升沿会给步进电机一个脉冲，步进电机接收到这个脉冲信号就会转动一个步距角。A+和A-为步进电机的驱动线，代表A相；B+和B-为步进电机的驱动线，代表B相。

3.2 加减速控制系统软件设计

本文采用Vivado平台，运用Verilog语言自顶向下进行程序设计。通过对步进电机原理的分析，脉冲频率可以控制步进电机运行速度的快慢，而频率的快慢取决于单位时间内脉冲数的多少，即在一个周期内，PWM高低电平的个数。每一个高电平输出一个脉冲。FPGA采用的是模块化设计，程序分为按键消抖模块(key_fitter)、迭代除法器模块(Divide)和步进电机模块(PWM)。其中，数据通过迭代除法器模块进行处理，得到所需的运动时间，寄存到quotient寄存器，再传输到步进电机模块，步进电机模块根据得到的运动时间确定减速点，即各个阶段的运动时间。按照每个阶段的脉冲需求，输出脉冲(PUL)。按键消抖模块用来消除开关的机械抖动。通过例化的方式将各个模块的输入与输出进行连接。因此在FPGA中实例化这3个模块，有利于代码的简化和修改，使整个系统的实时性以及灵活性得到显著的提高，从而实现步进电机运动状态的控制。程序例化后的RTL视图如图7所示。

图7 改进后的梯形加减速算法RTL视图

3.2.1 按键消抖模块

按键消抖[17]模块是为了消除按键的抖动。当按键按下时，一个按键不会立刻就稳定持续的接通，也不会一下彻底的断开，而是在闭合和断开的瞬间伴随了一连串的抖动。抖动时间的长短是由按键的机械特性决定的，一般为5～10 ms。这样会对步进电机运动时间t造成影响。本文采用延时消抖，首先定义一个记录按键状态的变量，然后读取按键的状态，延时后，再读取按键状态，如果两次状态一样则判断按键按下。

3.2.2 步进电机模块

1)梯形加减速设计。

步进电机控制模块需要实现梯形加减速，将梯形加减速分解成启动、加速、匀速、减速、停止5个部分。因此，代码的整体框架采用状态机。一共分为5个状态，分别为IDLE(空闲状态)、ADD(加速状态)、TOP(匀速状态)、SUB(加速状态)、STOP(停止状态)。通过判断标志位的状态来实现5个状态之间的跳转。如果标志位信息为1，就跳转至下一个状态，否则就保持当前状态。步进电机的启动需要一个启动频率，即步进电机开始转动的频率。步进电机的工作频率为零时，步进电机不会启动，当工作频率达到启动频率时，步进电机才开始启动。因此，加速阶段是从启动频率加速到Vmax对应的频率，减速阶段是从Vmax对应的频率(最大频率)减速到启动频率，然后步进电机停止运动[18]。

首先，判断当前步进电机的当前频率target是否与Vmax对应的频率target_max一致，若当前频率小于最大频率，则进行加速操作，加速度为100 Hz，此时设计一个计时器cnt_add_time用来记录加速操作的时间。若当前频率等于最大频率，则保持当前频率不变，此时，步进电机进入匀速阶段，匀速阶段的运行时间为cha=number-cnt_add_time。这里的number为迭代除法器计算出的减速点的时间点。该减速点为加速阶段时间和匀速阶段时间的和。匀速阶段结束后进入减速阶段，减速阶段的加速度为-100 Hz，并且减速阶段的运动时间和加速阶段的运动时间保持一致。减速阶段结束后进入停止状态。本系统设计的加减速周期为10 ms，即每过10 ms加速一次或者减速一次。因此需要设定参数CNT_10MS，当计数器计数的值和这个参数一致时，就执行一次加减速操作。CNT_10MS的数值和加减速周期有关。本系统所使用FPGA的晶振时钟频率为50 MHz，时钟周期为20 ns，因此CNT_10MS的数值为5000000。

2)分频器设计。

步进电机的持续运转需要一系列的脉冲来维持。因此分频器的设计可以产生连续的脉冲信号，获得所需要的脉冲频率。使用verliog语言进行分频计数设计，实现方式如下所示：

assign FRE_CNT=(50000000/target_fre)>>1；

其中50000000为FPGA晶振频率，target_fre为速度对应下的脉冲频率。再定义一个计数器cnt_pul，当cnt_pul计数的值为FRE_CNT-1’b1时，PUL进行翻转。在一个周期内，PUL的高低电平形成了一个个脉冲，如此重复下去，可以产生连续不断的脉冲信号。通过此法，可以将所需的脉冲数在10 ms这个周期内产生并发送给步进电机的驱动器。

3.2.3 迭代除法器模块

通过迭代除法器[19]可以将减速点计算出来。除法是乘法的逆运算，包括一系列移位和条件减法运算，其流程图如图8所示。先把除数左移一位，然后用被除数减去移位后的除数，结果为正，商的位置为1。再将余数左移一位减除数，判断结果的正负，如果结果为正，商数左移一位，最低位置为1；如果结果为负，商数左移一位，最低位置为0，舍弃余数。重复该移位操作直到移位次数达到设定的值，最后输出结果。在本文的设计中，根据步进电机模块中参数的位宽，设置被除数、除数和商的位宽都为48位。因此移位计数器的值为47，移位次数达到47次后输出结果。判断移位后做减法所得结果最高位的值，分辨结果的正负，从而进行与结果正负对应的操作。具体实现代码如下：

if(!remainder_temp[47]) begin

quotient_reg <= (quotient_reg << 1) + 1;

remainder_reg <= remainder_temp << 1;

end

else if(remainder_temp[47])begin

quotient_reg <= quotient_reg << 1;

remainder_reg = remainder_reg << 1;

end

count <= count + 1'b1;

迭代除法器模块的作用是根据接收到的步进电机位置信息计算出梯形加减速减速点，即步进电机何时进入减速。因此，步进电机可以根据实际工况，改变自己的位置信息，从而提高步进电机控制的灵活性，提高工作效率。

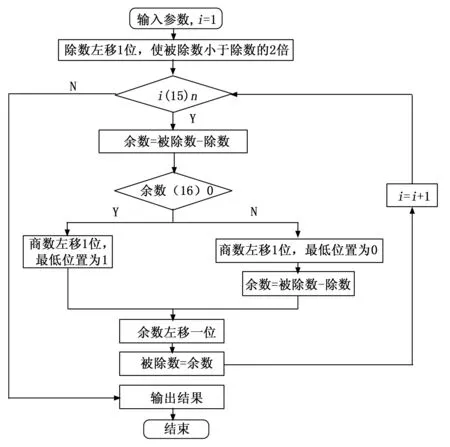
图8 迭代除法器流程图

4 仿真与实验结果分析

本文针对速度曲线的精度和减速点自适应确定分别进行仿真与实验。仿真平台为Vivado 2019.2。

4.1 速度曲线精度实验

实验设定目标位置为1085脉冲，起始速度为5脉冲/10 ms，最大速度的脉冲值为20脉冲/10 ms，加速阶段的加速度和减速阶段的加速度均为1脉冲/10 ms。仿真图如图9所示。从图9中可以看出整个脉冲频率曲线呈梯形，说明步进电机的加减速控制可以由该系统实现。

图9 梯形加减速仿真图

本文采用的实验平台由达芬奇A7系列FPGA、DM422驱动器、42步进电机和编码器组成，仿真实验平台如图10所示。

图10 仿真实验平台框图

当按下FPGA上的启动按键时，FPGA会将脉冲信号发送给驱动器，驱动器会控制步进电机运动，步进电机和编码器通过梅花联轴器连接，将编码器与控制板的引脚相连接，编码器会将步进电机的转速转换成脉冲信号通过UART串口发送到PC端。实验结果如图11所示。

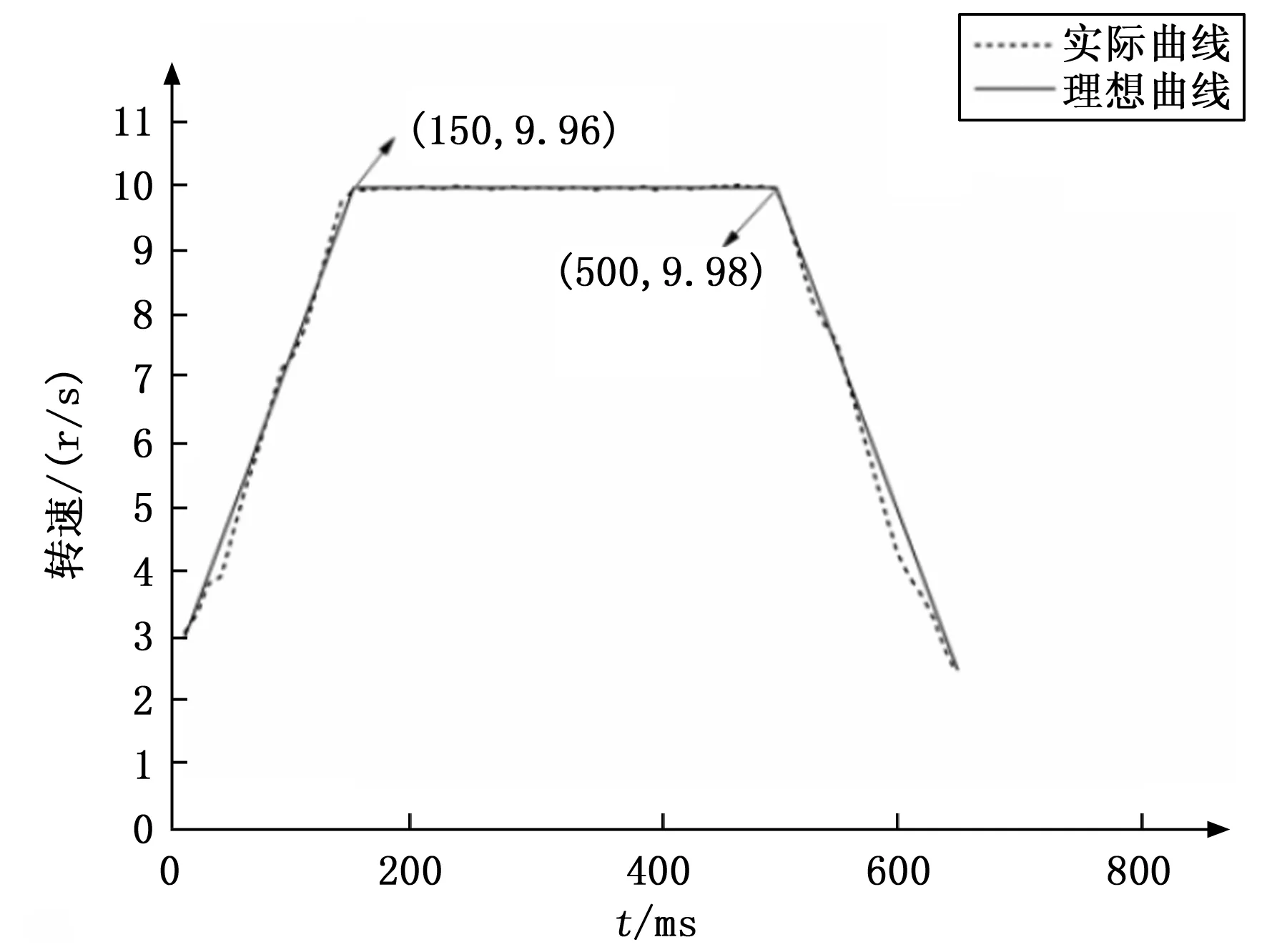
图11 实验结果

由图11可知，在加速阶段和减速阶段，转速的误差较小。到达最大速度时的数值和理想数值误差小。整个速度曲线平滑。在符合步进电机转矩特性下，改进的梯形加减速算法能够很好地实现步进电机梯形加减速。再对编码器反馈的数据进行处理和分析，得到理想速度曲线和实际速度曲线的转速差值，如图12所示。从图12可以看出，在一次完整的运动过程中，当t的范围为0～150 ms时，系统处于加速阶段，转速的最大误差值为0.56 r/s；当t的范围为150～500 ms时，系统处于匀速阶段，转速的最大误差值为0.04 r/s；当t的范围为500～650 ms时，系统处于减速阶段，转速的最大误差值为0.67 r/s。由于梯形加减速算法自身的局限性，在加速阶段和减速阶段会出现速度突变的现象。但整个过程的误差是偏小的，能够满足工况的精度要求。

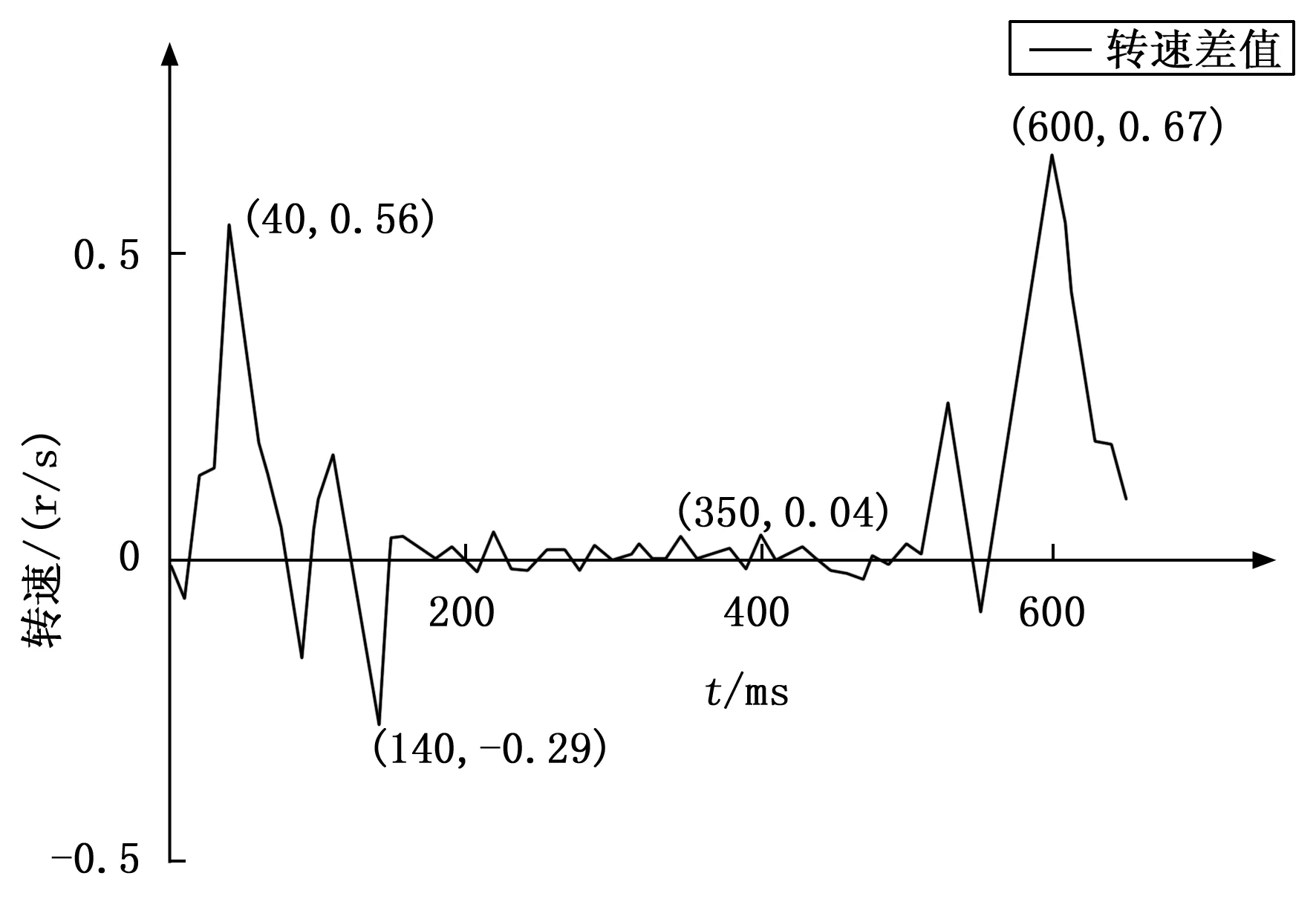
图12 理想转速与实际转速差值

4.2 减速点自适应确定实验

实验设定目标位置为1115脉冲，起始速度5脉冲/10 ms，最大速度的脉冲值为30脉冲/10 ms，加速阶段的加速度和减速阶段的加速度均为1脉冲/10 ms。仿真图如图13所示。由图13可知，通过迭代除法器计算出来的整数部分NUMBER-R0=333_333_333(ns)，实际减速点的时间为330_020_230.00 ns，理论减速点的时间为333_333_333.33 ns。由于步进电机有启动频率，在频率跳跃时，计数器会重新计数，这就导致起始速度的脉冲发射周期出现误差。但是，提高系统时钟后，能够减小这种误差。表1是系统时钟为200 MHz下测得的7个减速点。由表1可知，减速点的精确度最低为98.00%。说明减速点的确定精确度较高，能够达到系统的设计要求。同时，减速点是由本系统的算法计算出来，这就说明本系统对于步进电机不同的目标位置，都能够自行计算出减速点。在不同的工况下，该系统具有一定的自适应能力。

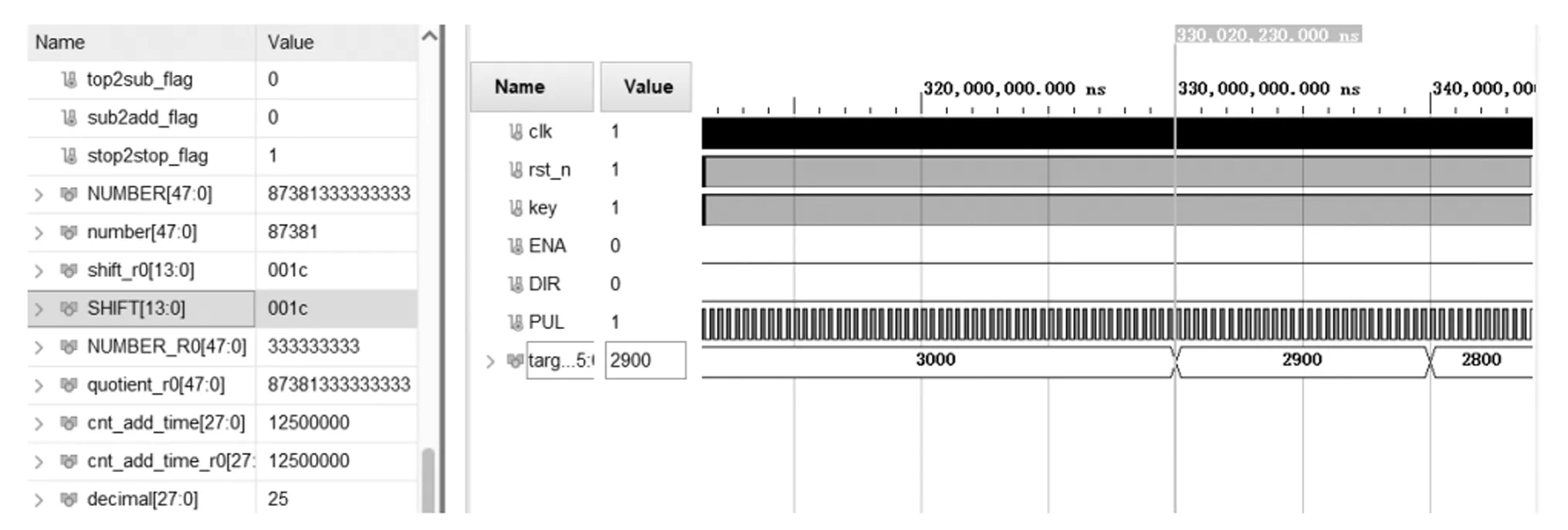
图13 减速点仿真图

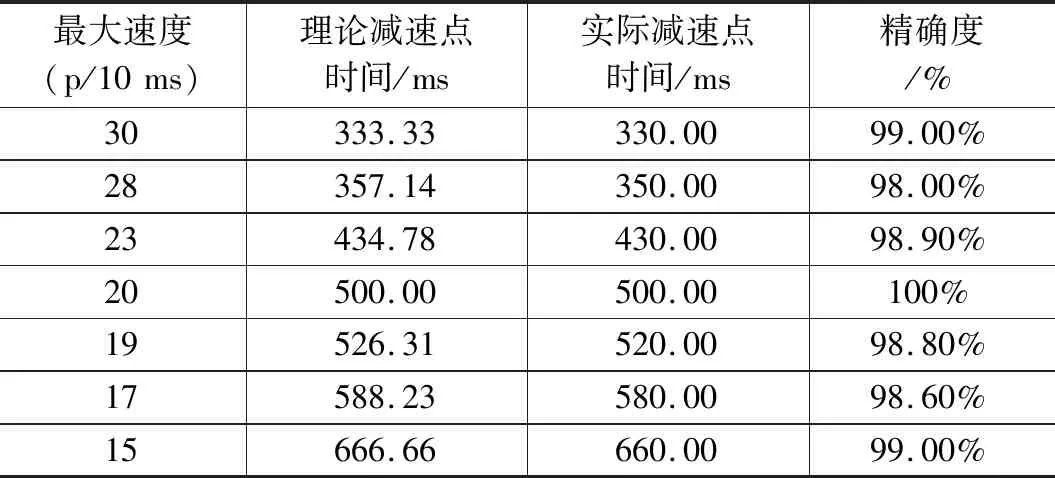
表1 减速点的确定时间

5 结束语

本文通过对步进电机原有的梯形加减速算法分析，对其进行改进，改进后的梯形加减速算法通过时间来确定减速点。实验结果表明，改进后的梯形加减速算法在加速阶段和减速阶段理想曲线和实际曲线误差较小。改进后的步进电机梯形加减速控制能够保证精度和可靠性，实时性高，代码实现简单。在步进电机的位置改变后，能够自动计算出减速点，具有一定的自适应能力，大大提高了其灵活性，提高了加工效率，对于优化裁切机运动控制系统的轨迹，具有一定的意义。现阶段该系统是开环控制，后续可以将编码器的数据反馈给FPGA做成闭环控制的系统，能够提高加减速控制的精度，同时可以利用FPGA并行处理的优点，把单轴拓展到多轴上实现裁切机的加减速控制。