圆柱绕流特征频率相似性研究∗

李定远 方 斌 李一鸣 关惠仁

（海军工程大学舰船与海洋学院 武汉 430033）

1 引言

圆柱及圆柱群绕流现象作为钝体绕流中的经典问题，在自然界中广泛存在，并被大量运用于海洋结构、船舶工程、航空航天、土木、机械等多种工程领域中。当流体流经圆柱类结构物时，在一定流动工况下，会在结构物的后方呈现旋涡脱落的现象。这些旋涡周期性地交替出现，导致结构物在垂直于来流方向上受到周期性变化的作用力，致使结构物产生振动，圆柱后会产生大范围的流动分离和涡脱落的现象，压差导致阻力的增加，同时产生噪声［1］。国内外学者对圆柱绕流开展了大量研究。Revell等［2］研究了圆柱绕流阻力和流噪声之间的关系，其研究结果为后来学者提供了参考和借鉴。张翰钦等［3］以三维圆柱为研究对象，使用Lighthill声类比法研究其绕流发声问题，得出进行辐射噪声预报时，FW-H积分法和边界元法基本相同的结论。刘国庆等［4］系统的对圆柱绕流的水动力噪声进行研究。李浩鸣等［5］对低雷诺数下二维与三维圆柱绕流进行了数值计算，对比发现随着雷诺数的增加二维与三维状态下流场存在明显的差别，尤其是在圆柱尾涡的形态上。杨志刚、刘志超等［6～7］对有限长圆柱绕流气动噪声源特性进行了研究其结果表明在有限长圆柱绕流场中，以偶极子声源为主，单极子声源可以忽略不计，四极子源项的值比偶极子小1个～2个数量级。王毅刚等［8］开展了圆柱绕流近壁面处气动噪声源识别的研究，该研究在探索识别圆柱绕流气动噪声源方法的同时，也为准确识别气动噪声源特征提供了有效的方法。王毅刚等［9］从辐射声功率入手，推导得出气动声学相似的原型和模型的远场声压级转换关系，但其所求的声压级为总声压级，没有考虑和频率之间的关系。

当研究目标实物较大时通常采用缩比模型进行研究，这样不仅可以节省研究成本，还易于试验的开展，例如船模阻力试验已经建立了比较成熟的缩比模型试验仿。但是，水下物体流噪声的缩比模型试验，目前还有很多困难需要解决，主要原因在于：1）声学物理量量级较小，容易受到试验环境的干扰；2）流噪声的产生与流体动力性能密切相关，需要同时满足流体动力相似和声学相似，而流噪声缩比试验所需要的稳定速度和安静环境，往往很难同时满足；3）流噪声常常与机械噪声、螺旋桨混合在一起，很难分离出来单独研究；4）水中开展流噪声试验的成本相对高昂，试验难度也较大。针对上述情况，在已有研究成果的基础之上，开展相同介质中圆柱流噪声特性的相似试验研究、不同介质（空气和水）中圆柱流噪声特性的相似关系数值仿真研究，探索水下物体流噪声相似试验的新方法，为潜艇、水下航行器声学试验等工程问题提供支持。

2 理论分析

由于流噪声的产生与流体动力特性密切相关，因此流噪声相似首先应满足流体动力相似。根据流体力学中相似理论的研究，分别建立几何相似、运动相似和动力相似关系，并得到相关的相似准数St数、Fr数、Eu数、Re数和Ma数。两个相似流动之间某一个相似准数在数值上相等表示与之对应的某一种力成比例，即对于这种力是动力相似的。由于流噪声相关的五个相似准数所要求的条件相互矛盾，不可能得到完全相似的现象，这时只能满足其中主要相似准数的要求，即部分相似。

对于本文所讨论的圆柱绕流噪声问题：1）粘性作用是主要，而重力作用的影响是次要的，因此需要满足雷诺数Re相等，而忽略傅汝德数Fr；2）杨志刚等人的研究也表明［6，8，10～11］，圆柱绕流噪声的噪声源主要是偶极子噪声，圆柱绕流噪声的特征频率与尾涡脱落频率近似相等，也与最大声压级对应的斯特劳哈尔数相等，所以应该满足St相等；3）欧拉数Eu反映的是压力对流体的作用，如空泡现象、空泡阻力等，对于流噪声问题先不分析空泡的影响，忽略欧拉数Eu；4）对于低速问题，流体包括空气和水的压缩性并不明显，因此可以不考虑流体的压缩性影响，忽略马赫数Ma。

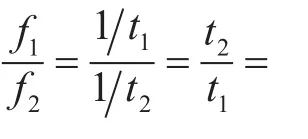
表1 相同介质雷诺相似时的相似条件（ρ1=ρ2、μ1=μ2）

表2 不同介质雷诺相似时的相似条件（ρ1≠ρ2、μ1≠μ2）

3 实验研究

3.1 实验条件及实验模型

对相同介质（空气）中不同比例圆柱绕流噪声开展试验研究，测试在海军工程大学舰艇用消声风洞中进行。消声风洞包括消音室和洞体结构两大部分，消音室采用全消音室形式并含实验测试段。消声风洞如图1和图2所示。

图1 消声风洞实景图

图2 消声风洞实验测试段

消声风洞主要技术指标为实验测试区域长10m×宽8m×高6m；喷口直径2m；实验段长度4.4m；风速V≤60 m/s；中心区域湍流度 ≤0.2%；来流不均匀性<1%；截止频率 ≤50Hz、吸声率>99%。

主要采集设备包括：声望MPA201型声压传感器，为减少风洞中气流对声学测试的影响，声压传感器均安装了鼻锥，如图4所示；采用NI的PXI机箱进行数据采集。

图3 声望MPA201声压传感器及其安装图

声压测点位置如表3和图4所示。

表3 声压测点位置表

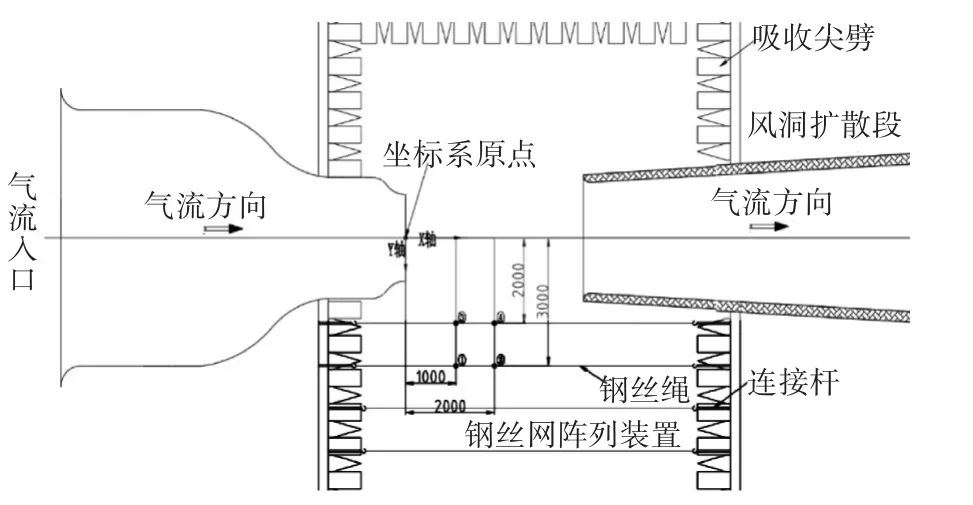
图4 声压测点位置示意图

根据研究需要，制作了直径为19mm与38mm的两个圆柱模型。圆柱实验模型紧贴在出风口，上下两端超过喷口外延，并进行固定。其安装图如图5所示。

图5 圆柱模型风洞安装图

3.2 实验工况以实验结果

3.2.1 实验工况设定

本实验所制作的模型为的几何相似比为1：2，为了保证其雷诺相似，两个圆柱模型进行实验的风速设定如表4所示。

表4 不同圆柱模型实验风速设定表

3.2.2 实验结果分析

因为距离对特征频率影响微乎其微，所以对01测点的数据为分析对象进行特征频率的分析。图6（a）～（e）为五个工况下两个圆柱模型实验的声压级-频率对比图，由图可见圆柱绕流噪声的特征峰值较为明显。不同模型特征频率之间的关系分析见表5，从表中所列数据可以看出，当模型几何尺寸之比为1：2，且满足雷诺相似时，特征频率近似满足4：1，五个工况下误差均小于10%，其中工况1的误差最大为8.33%，其他工况下误差均在5%左右，或小于5%。实验结果总体来说与理论值吻合较好。工况1误差较大的原因可能是由于38mm圆柱模型实验的风速较低，其特征频率本身较小，收到背景噪声的影响较大，所以误差较大。

图6 不同工况下两个圆柱模型实验的声压级-频率曲线

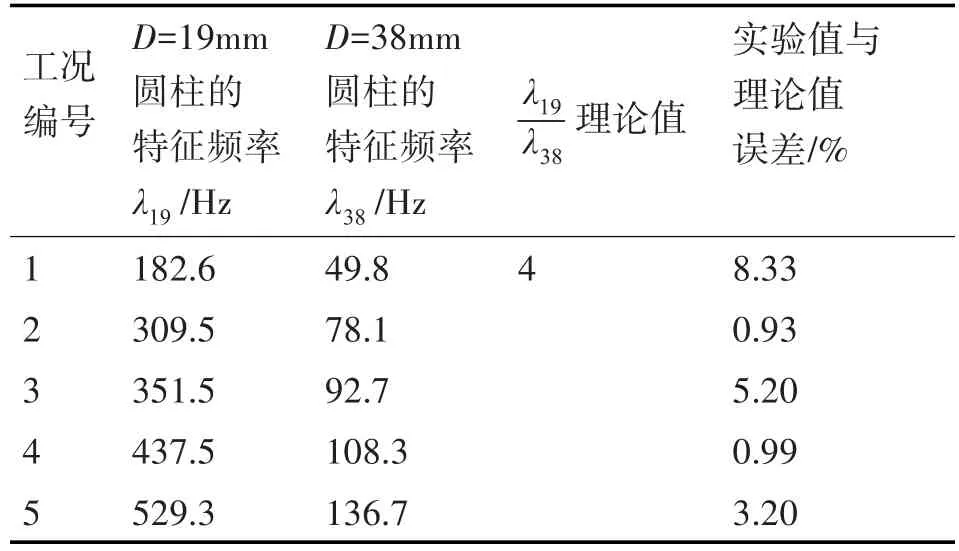
表5 特征频率之比的理论值与实际值对比

4 仿真计算

圆柱绕流噪声相关的仿真计算已有大量学者进行了研究。刘聪尉等［12］将计算气动声学的理论和算法成果运用到水动声学领域，建立的粘声分离计算方法。顾信忠等［13］研究了一种将离散涡方法（DVM）和涡声理论结合起来计算低马赫数、高雷诺数流场气动噪声的方法，计算点的总声压级与实验值及其他数值计算结果都比较吻合蔡建程等［14］对圆柱绕流气动声的偶极子源与四极子源进行提取，对圆柱绕流气动声进行了定量预测。王芳等［15］结合Lighthill波动方程和格林函数解，选择围绕固体边界的光滑边界作为积分边界，推导获得一种基于可渗透边界的气动噪声计算模型，并对层流圆柱和湍流圆柱气动噪声进行数值模拟。数值计算结果显示层流圆柱和湍流圆柱噪声分别与直接数值模拟（Direct Numerical Simulation，DNS）结果和进行高精度流场计算的FW-H方程所得结果吻合。张小锋等［16］以三维刚性圆柱为研究对象，开展了基于大涡模拟和Lighthill声类比理论的混合数值模拟方法研究，计算量圆柱绕流的水动力噪声，本文的水动力噪声计算主要参考其计算思路。

4.1 模型建立及网格划分

4.1.1 流体建模及网格划分

第三，完善相关政策。青岛市应该进一步完善户籍制度，为本市的城市化进程提供制度保障，尽早实现城镇化与工业化的同步发展。

流体计算域建模如图7所示，圆柱直径D为19mm，半圆形入口取为5D，下游尾流区取为25D。对圆柱壁面和尾流区进行加密，第一层网格的距离为0.007mm，计算域体网格如图8所示。

图7 计算域

图8 计算域体网格

流体为气体时，取温度为15℃，密度为ρ=1.23kg/m3，动力粘性系数 μ=1.78×10-5pa∙s；流体为液体时，取温度为15℃，密度为ρ=999kg/m3，动力粘性系数 μ=1.05×10-3pa∙s。先进行定常计算，再以定常计算的结果作为大涡模拟的初值进行非定常计算。

4.1.2 声学建模及网格划分

采用声学有限元与声学无限元相结合的技术，声传播区只需略大于声源区即可，声传播区以及声源区网格划分如图9所示。

图9 声场网格

4.2 计算工况以及计算结果

4.2.1 计算工况

对于不同介质中相同模型的流噪声相似性问题，本文设计如表6所示工况进行数值计算。本文以工况1、3为相似组1，工况2、4为相似组2。

3.2.2 计算结果

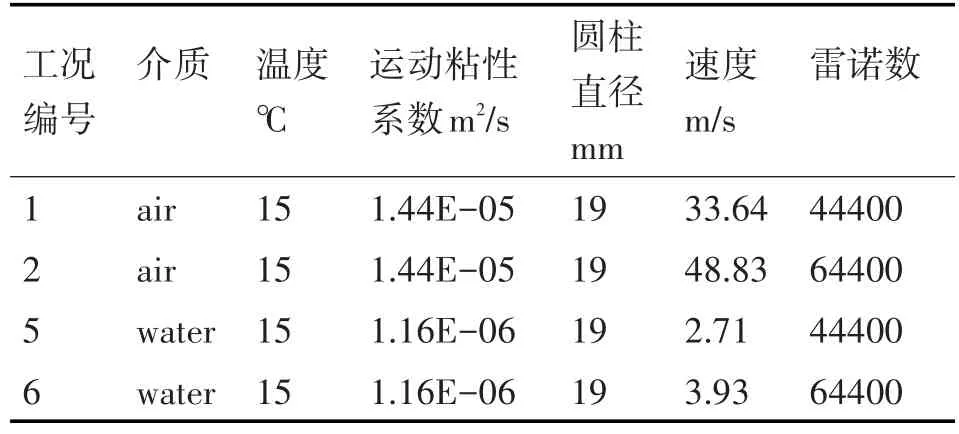
表6 设计工况

图10 相似组1及相似组2的声压-频率曲线对比图

表7 特征频率之比的理论值与实际值对比

从表7中可以看出，两个相似组数值计算结果与理论均存在一定的误差，但该误差在10%左右。下面对引起误差的原因进行分析。

图11所示是流体为空气时CFD计算的涡量图，图12所示是流体为水时CFD计算的涡量图，将两图进行对比可以发现，图10尾涡有明显的截断现象。该尾涡截断现象的出现可能是由于在计算空气和水两种流体时采用的是相同的模型相同的网格，在雷诺相似的情况下，由于两种介质的性质差异，其尾涡的长度是不同的。根据上述分析，水中的噪声计算较空气中会更准确一些。空气尾涡丢失的可能是对噪声高频贡献较大的部分涡，，所以导致空气中计算得到的噪声频率偏低。相似组2与相似组1的情况类似。

图11 流体为空气时CFD计算的涡量图

图12 流体为水时CFD计算的涡量图

5 结语

本文采用风洞试验的方式，对相同介质中不同比例的圆柱模型绕流噪声相似性的问题进行了研究，试验结果表明两个圆柱模型比例，在满足雷诺相似的前提下，其绕流噪声特征频率的比值。且试验结果与理论预期误差较小。