新型磁致伸缩扭转导波传感器在铜管中的实验研究∗

许鉴鉴 王悦民 邱增城 陈 昂

（海军工程大学动力工程学院 武汉 430033）

1 引言

管道在船舶、化工、城市建设中广泛应用，但是由于部分管道工作环境较为恶劣，管道内外部在高温高压等条件下，易产生裂纹、腐蚀、锈蚀等缺陷，缺陷若不能被及时检测出来，将会导致诸如管道破裂、管道系统瘫痪等严重后果，给社会和企业带来较大损失甚至人员伤亡。管道的无损检测技术中，通常采用逐点扫描的方式，其检测效率较低、速度较慢。而导波无损检测技术对管道可以进行长距离，非接触式检测；并且能够有效消除管道表面有包覆层等限制条件对检测结果的影响。因此得到国内外专家的高度重视。导波在管道中传播时分别有以下三种不同的模态：纵向模式L［0，m］（m=1，2，3…）；扭转模式T［0，m］（m=1，2，3…）；弯曲模式F［n，m］（n=1，2，3…，m=1，2，3…）［1］；其中，n为周向阶数，m为模数。在各种模态中，只有弯曲模态是非轴对称模态，其余的两种模态是沿管z轴的对称模态。当前国内对于管道的磁致伸缩导波检测多见于纵向模态导波。但是采用纵向模态（例如L（0，1））对管道进行检测，则存在频散，以及对管道的轴向缺陷信号较弱等缺点。相比纵向模态，T（0，1）模态扭转导波具有非频散特性，该模态导波不仅克服了纵向模态导波的不足，而且在管道远距离传播中能量衰减较弱。这种特性使得T（0，1）扭转导波在对管道进行无损检测上比其他模式的导波具有更高的灵敏度。而扭转导波产生的位移为周向位移，使该模态导波在对管道纵向裂纹的检测上有着其他模态导波所没有的优势。

管道扭转模态导波传感器大致可分为以下三种：压电式［2］、磁致伸缩式和洛伦兹力式［3］。磁致伸缩式［4］对管道自身材料有要求，必须为铁磁性材料，利用管道本身的磁致伸缩效应来进行缺陷检测，这种传感器常用于管道表面带有包覆层或表面生锈等情况。对于非铁磁性材料管道，其材料不具备磁致伸缩效应，需要在管道外表面上粘贴磁致伸缩条带进行能量的转换。国内外专家对扭转模态导波传感器进行大量的研究和试验。Cho S H等［5］设计的传感器包含一个特制的回折线圈和铁钴条带组成，其激励频率可以达到1MHz～2MHz，主要是用于检测一些管道的微小缺陷。Kwun［6］将磁化过的铁钴条带用环氧树脂粘贴在被测管道外表面上，然后用激励线圈产生一个轴向的交变磁场，在被测管道中成功激发出扭转导波。Kim H J等［7］提出了一种等效分布力模型用来描述铁钴条带传感器的工作原理，模型的准确性得到了实验结果的验证，该模型可作为多数磁致伸缩导波传感器结构优化的理论依据。在国内，张小伟等［8］设计了一种螺旋梳状磁致伸缩条带传感器，磁致伸缩条带先用永磁体磁化过后，将其在管道外表面呈螺旋状粘贴，接着采用复合梳状线圈缠绕在条带上，该传感器成功激发出信噪比较好的弯曲模态导波，并且可以控制弯曲导波传播的方向。刘增华等［9］设计一种新型的纵向导波传感器，该传感器与传统传感器不同的是它的线圈是由多段回折线圈组成，不仅能在管道中可以激发出L［0，2］模态导波，且与传统传感器进行对比，该传感器信噪比更好。蔡瑞等［10］提出一种新型的金属小径管损伤电磁超声导波检测的高效混合仿真方法，采用了解析法和有限元法，能够实现对传感器的快速求解。朱龙翔等［11］先将铁钴条带用永磁铁进行磁化，然后让条带与轴向方向成一定角度粘贴在被测管道外表面，在管道中激励出扭转导波，并得出结论在频率为31kHz左右时，信号的信噪比最好。但采用这种方法产生的扭转导波只有在30kHz附近的频率点处才能得到较好的信噪比。本文设计了一种在管中产生较高频率扭转导波的传感器，并对其在铜管中的应用进行了试验研究。

2 管中扭转导波的频散特性研究

弹性波在固体传播过程中的弹性动力学运动方程为［12］

等式中，u为位移矢量；ρ为材料密度；λ和μ均为Lamb常数。

假设该弹性管道为空心直管，且均匀及各向同性，其内径为a，外径为b，应力自由边界条件为：当r1=a，r0=b时，应力 σrr=σrz=σrθ=0。求解空心直管中导波的位移场，可知其解为

等式中，ω为圆频率；k为波数；ur、uθ、uz分别为径向、周向和轴向位移分量；分别为由Bessel函数构成相应的位移幅度。

求解导波在管道中的运动方程，即为求解以下频散方程的解：

其中，C11，C12，…，C66为 α、β的Bessel函数，

当n=0时，导波的模态为轴对称，频散方程可分解为以下两个子行列式的积：

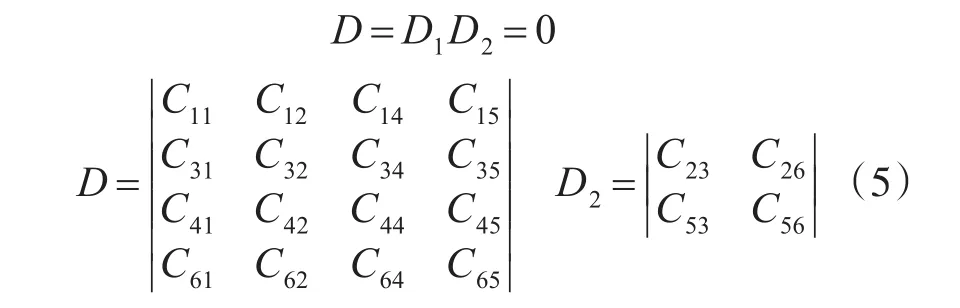
D1=0和D2=0分别对应于轴对称纵向模态L(0 ,m)和扭转模态T(0 ,m)。

通过以上公式可计算求得，导波在铜管中的频散曲线，如图1所示。铜管外直径为60.5mm，壁厚为5.5mm，弹性模量为119Gpa，密度为7.6×103kg/m3，泊松比为0.32。

从图1可得，在整个频率范围内T(0,1)模式扭转导波的群速度为一个恒定值，也就是说扭转导波在传播过程中不会发生频散。因此T（0，1）模式扭转导波在管道中的传播波形不会发生较大变化。

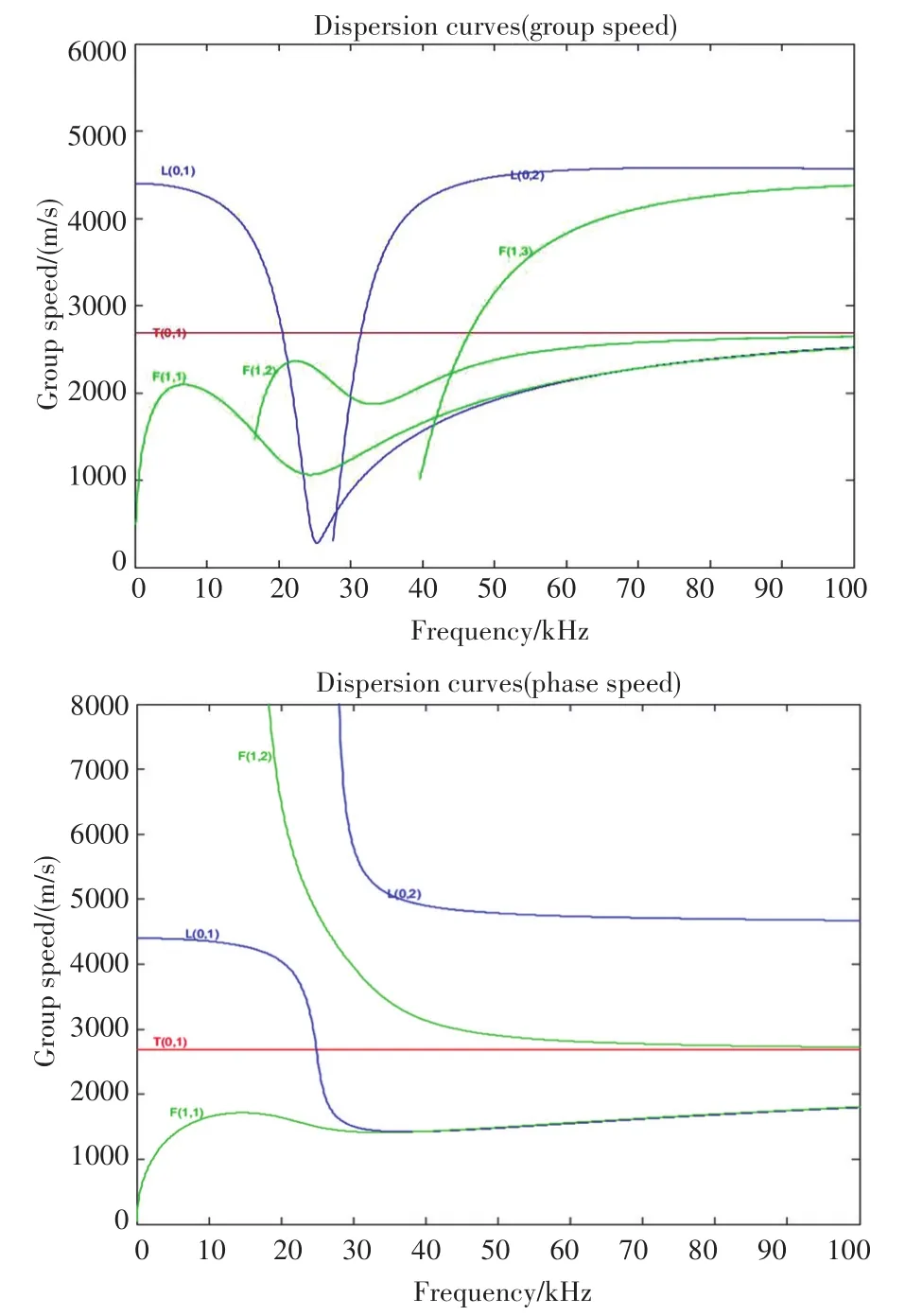
图1 铜管中的频散曲线

3 磁致伸缩扭转导波传感器的实验研究

3.1 实验装置

实验装置的大致结构如图2所示。图2（a）为系统装置示意图，该系统包含传感器、铜管、计算机系统；而传感器由铁钴条带、激励线圈和永磁铁三部分组成。首先由信号发生器产生激励信号，再通过功率放大器将信号进行放大，并作用于激励线圈，然后由激励线圈产生交变磁场，利用铁钴条带在变化磁场中的磁致伸缩效应，最后在铜管中成功激励出扭转导波。当管道中的扭转导波通过接收线圈的区域时，扭转导波作用于接收线圈处的铁钴条带，再利用逆磁致伸缩效应通过接收线圈将接收到的扭转导波转化为电信号输入到计算机进行存储和显示。如图2（b）所示，激励传感器、接收传感器都置于铜管左端，而且两者之间距离很近，因此，相当于扭转导波在管道一端入射，同端激励、同端接收。

图2 试验装置示意图

3.2 磁致伸缩扭转导波传感器的设计

使用铁钴条带粘合在铜管表面，该材料具有很大的磁导率和磁致伸缩系数，为了给包覆在管子圆周上的条带提供均衡的静态周向磁场，将永磁铁置于铁钴条带上，并在整个圆周上均匀分布，这样就保证了永磁体产生的磁通量大部分沿着铁钴条带的长度方向通过铁钴条带，于是在条带中产生周向磁场。激励线圈覆盖在铁钴条带上，为产生扭转波，由激励线圈提供电流，在轴向产生动态磁场。传统的螺线管式线圈当电流频率较大时，其感抗会很大，电流变小，磁致伸缩效应变小，导致信噪比较差。给线圈通电时，每隔一个线圈改变其电流的方向，这样，就能解决感抗太大的缺点；同时，将线圈间隔定为设计频率扭转波的半波长，就能够使每个线圈产生信号正向叠加，从而得到加强的有用信号，增大信噪比。当同时施加在条带上的静态和动态磁场相互正交时，条带中就产生了剪切变形，并且该剪切变形通过剪切耦合剂传递到波导中，于是，管中就产生了扭转波。图3为传感器实物照，其中图3（a）所示为传感器线圈的缠绕图，图3（b）为传感器安装在管路上的实物图。

图3 扭转波传感器

3.3 实验结果及讨论

本实验中使用的被测铜管为完整无缺陷管道，铜管长度为3.03m，外直径为60.5mm，壁厚为5.5mm。条带长度为管道表面圆周长，宽40mm，厚0.15mm，激励线圈和接收线圈都为每股线圈4匝，一共四股。激励传感器、接收传感器都置于管道右端。使用5个周期经汉宁窗调制的正弦信号作为激励信号。其表达式如下：

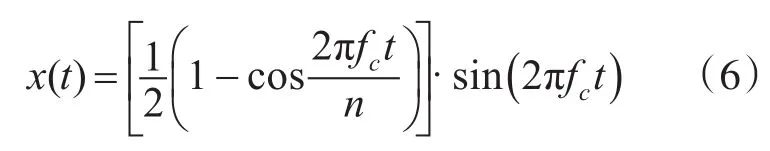
设计频率为91kHz的传感器在不同激励频率下得到的信号如图4所示。

由图4可知，各激励频率在2ms～3ms间的相同位置接收到了它们的一次端面反射信号，在4ms到5ms间的相同位置接收到了它们的二次端面反射信号，而一次反射信号与其二次反射信号之间的时间间距都稳定在t=2.387ms。实验中铜管的长度为l=3.03m，则信号波包的速度可由下式算出：

由频散曲线可知，在此铜管中T（0，1）模式扭转导波的群速度v′=2875m s，v和 v′基本一致。同时，分析各频率下信号的幅值可知，在传感器的激励频率与其设计频率相一致时，信号的幅值最大，信噪比最大。因此可以确定，本实验中激发出的该信号即为T（0，1）模式导波，最佳频率点正好是传感器的设计频率点。

不同设计频率的传感器激励频率与各自设计频率一致时，得到的扭转波信号如图5所示。

由图5所示可知，传感器设计频率与激励频率一致时，当频率大于91kHz时，随着频率的升高，扭转波信号的幅值相应的降低；频率为200kHz时，信号的三次反射信号已经基本衰减到0。这是因为导波的频率越大，管壁材料的阻尼对导波的衰减作用就越大。由此可知，采用这样的传感器设计，确实可以很明显地提高导波的频率，但当频率达到200kHz时就已经很难分辨出反射信号了，这不利于对管中缺陷信号的定位。

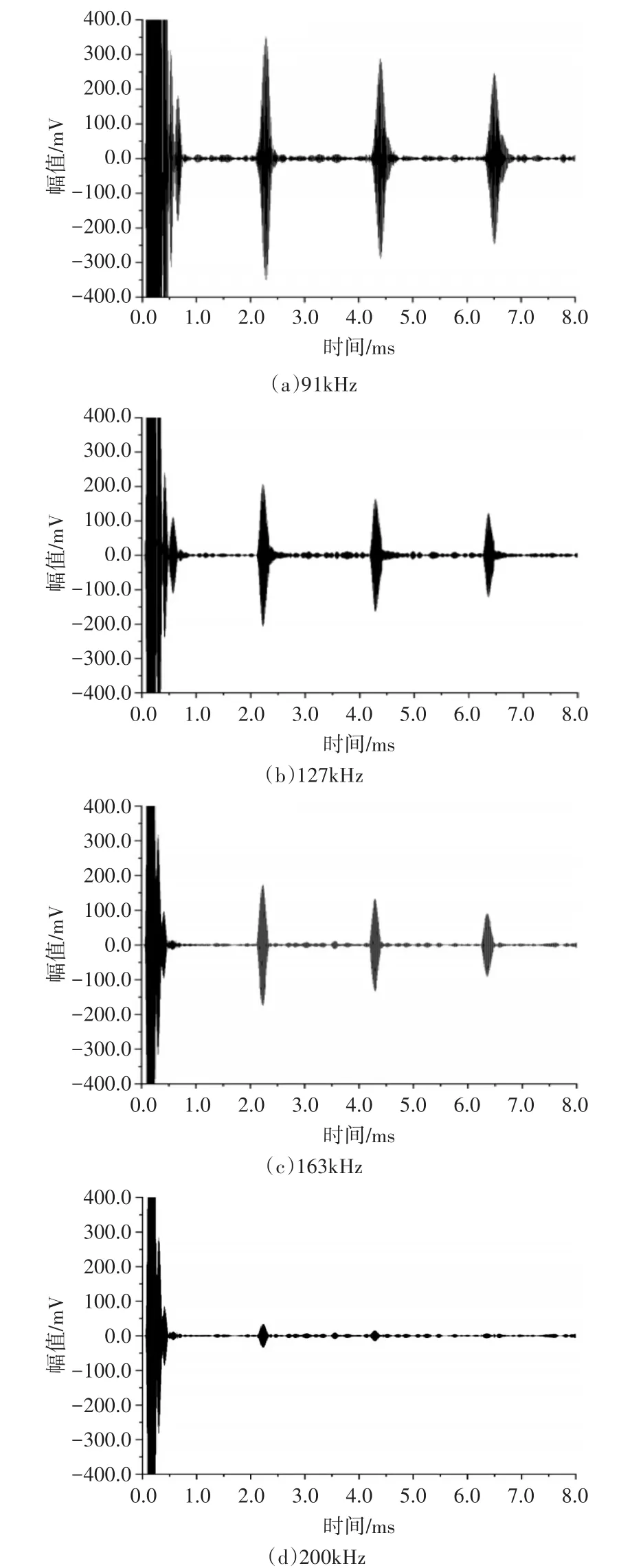
图5 传感器设计频率与激励频率一致时的扭转导波信号

4 结语

对当前国内外对磁致伸缩扭转导波传感器的研究现状进行了概括，并通过计算扭转导波在实验样管中的频散特性，设计了一种新型的扭转导波传感器，并对该扭转导波传感器进行了实验验证，成功地在铜管中激发出了信噪比良好的T（0，1）模态扭转导波信号。本文先采用不同激励频率对某一设计频率传感器进行实验，将得到的信号进行对比，研究不同激励频率对扭转导波信号的影响，实验表明，对于同一个设计频率传感器，只有当激励频率与设计频率相同时，其激励的扭转模态导波信号的幅值及信噪比最好。同时实验数据表明，对于本实验使用的管道来说该传感器的最佳设计频率为91kHz，但是不宜高于200kHz。