基于气象条件改进的CA和GM（1，1）组合交通流预测模型构建与分析∗

芮伟 谢泰 沙琨

（海军军医大学海军卫生信息中心 上海 200433）

1 引言

目前，城市交通问题日益突出，积极推动智能交通信息系统（ITS）建设是解决问题的有效途径之一。而城市道路交通流量的预测是智能交通系统的重要基础，为个人出行服务、各个区域之间交通信号的联合控制、制定特定的出行计划和城市道路建设规划管理分析等各个场景进行数据支撑。因此，构建科学的交通流预测模型，以实时和历史交通流数据为基础，对车流量预测这一关键问题进行深入研究分析，可以为缓解和预防城市交通拥堵提供有效帮助。

交通流理论［1］是多学科交叉的一门学科，通过物理学、统计学、力学、交通工程等多学科的协同分析，可以实现交通流准确、快速的预测。为了更好地进行交通诱导和交通控制，需要及时准确地掌握交通流预测信息和数据。关于交通流预测，国内外学者已经开展了一系列的相关研究，其中元胞自动机［2］（Cellular Automaton，CA）交通流模型能够根据实际情况灵活设置车辆运行规则，具有良好的并行性。而灰色GM（1，1）模型可以对不规则的原始数据进行生成，得到规律性强的生成序列，且所需的数据量少，精度高。因而两种模型在交通流研究领域都得到了广泛应用。冉磊、蔡远丽［3］在一维交通流元胞自动机Nasch模型的基础上，提出一种改进的一维敏感驾驶元胞自动机交通流模型。钱勇生、曾俊伟［4］等建立了有意外事件影响的车道管制下的高速公路元胞自动机交通流模型，该模型考虑了交通事故和养护路段等意外事件对高速公路交通流的影响。葛红霞、戴世强［5］在NaSch模型的基础上，提出一种应用智能交通系统的交通流元胞自动机模型，模型考虑有效间距及刹车灯的作用，并引入可变安全间距的新概念。张敬裔，王晓原［6］将灰色模型与RBF结合并应用于短时交通流预测中，取得了较好的预测效果。游中胜、何丽等［7］对于城市短时交通流的预测提出基于改进累减还原方法的灰色模型，模拟及预测性能都取得了一定的提高。

2 模型建立

2.1 基于CA的交通流预测模型

Wolfram参照已有模型，通过大量的试验分析与理论论证提出了184号模型，其实质上属于一种一维交通流CA模型。该模型中车辆具有多种状态，即向前进行元胞移动，或者停留在现有元胞，对于自由流和堵塞阶段可以进行很好地描述，该模型的缺点是对于实际情况中的驾驶特性没有加以分析，因此，更多地停留在理论分析阶段，对于指导实际交通没有太大优势。1992年，德国学者Nagel和Schreckenberg在184号模型的基础上构建了NaSch模型，该模型与184号模型相比，最大的特点在于将实际系统中车辆的加速与延迟等加入到模型之中。

NaSch模型作为CA模型的一种，元胞状态都是离散的，包括其时间、空间以及速度等。假设一段距离为I的道路，将其离散化，分散成一个一个的网格，也就是元胞，任何一个元胞的状态只有两种情况：空、车辆占据。本文给出具体的演化规则如下。

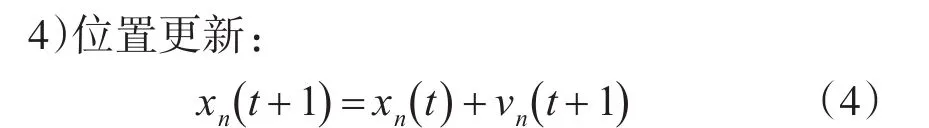
上面，xn和vn分别代表第n辆车的位置与速度，dn=xn+1-xn-lveℎ表示第n辆车与前面车辆的距离，lveℎ则代表了车辆的长度信息。

在NaSch模型中，其具体的演化规则是：1）描述的是车辆加速，表示所有的驾驶者都希望在道路中以最大的期望速度进行行驶的行为；2）为了避免发生交通事故，保持与前面车辆的安全距离，需要在某些时刻降低行驶速度；3）在某些特殊的情况下，基于安全的考虑，以一定概率进行减速行驶；4）车辆位置的更新。

2.2 基于GM（1，1）的交通流预测模型

邓聚龙教授通过大量分析论证，提出并创立了灰色系统理论［8］。本文在具体研究分析过程中，选取了GM（1，1）模型，运用时间序列预测方式，对时间序列构建完善、可行的模型并预测未来值。

首先，利用合理的方式来检验交通流时间序列，使其能够利用灰色模型来实现建模，目前，初始序列为已知条件，具体为

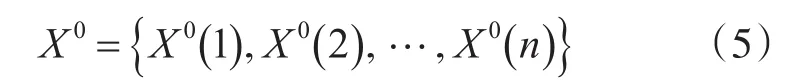
计算该时间序列的级比为

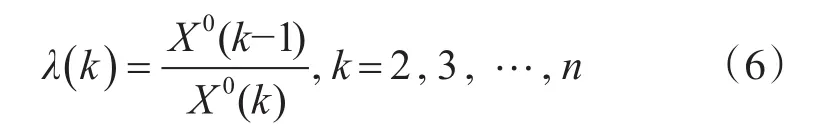
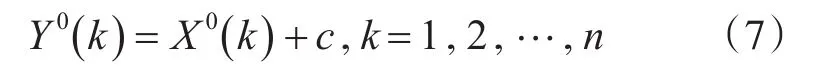
此时数列的级比为

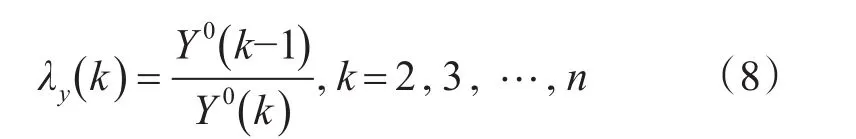
国内外众多学者与专家为了进一步提升灰色模型的预测精度，将灰色模型建模机理作为着手点，结合实际情况，对灰色理论GM（1，1）模型进行了优化改进。刘常丽、屈绍建等［9］专家与学者主要借助模型背景值进行优化处理。黄克［10］则以递推法作为基础，通过大量的分析论证，求出一种简单、便捷的序列长度计算方式，从多个步长存在较大差异的GM（1，1）模型之中确定最佳预测步长，进而提升预测精度。

经过改进优化的方式绝大多数是以建模过程中与之相对应数据序列为重要基础，对于GM（1，1）模型参数的选取，式（8）中列出数据广义级比间存在的关联未进行深入的考虑与分析。因此，本文采用了孙波军、尹伟石［11］提出的一种灰色模型算法，该模型基于日周期变化的数据特征，可自动选择步长来进行城市道路交通流预测。

交通流数据存在一定的周期性变化规律，间隔单位一般为日，此种周期特性可以认定为不同日期下交通流数据在任一时刻与之呈对应关系的数据级比相近。第一步，通过科学合理的方式来分析交通流历史数据级比；第二步，对GM（1，1）模型选取不同步长，对交通流进行预测；第三步，对步长不同模型参数a相对应的(1+0.5a)/(1−0.5a)值进行深入的观察与分析，选择同交通流历史数据级比最相似的模型作为预测模型。模型预测步骤如下。

Step1：确定 GM（1，1）模型步长选择范围(s,d),s>3；

Step2：对历史上t时刻交通流数据级比σ1(k)借助式（6）进行全方位、多层面的分析运算，k值则在区间（s，d）间进行选取。若为多个日期的数据，那么需要选取不同日期数据的平均数值；

Step3：利用科学合理的方式来精准预测t+1时刻交通流，然后把t定义为最后一个数据，那么向前则以此选取s,s+1,…,dt个数据，对于不同步长的数据，通过恰当的方式，并求出与之相对应的发展系数 as,as+1,…,ad，构建GM（1，1）模型；

Step4：从 as,as+1,…,ad与之相对应的(1+0.5a)/(1−0.5a)值之中，结合实际情况，确定与σ1(k)最相近的数值，并将其对应的步长定义为预测步长，然后充分利用该步长的GM（1，1）模型来精准预测t+1时刻交通流，并得出具体的预测值。

2.3 基于气象条件改进的CA和GM（1，1）组合的交通流预测模型

交通流特性［12～14］往往会受到多方面的影响，气象条件就是其中不可忽视的因素之一，不同气象条件会对车辆的速度、密度、流量等造成一定影响。单个模型预测的处理能力较差并且实用性较低，不能充分考虑到各种因素。基于此，本文将集成预测思想融于其中。

集成预测模型［15］的思想可以概括为结合实际情况，对不同预测模型进行组合处理，即赋予其不同的权值系数，并从各模型系统之中提炼一些真实、全面、有效的信息数据，充分应用各模型预测结果，对预测误差、预测风险实施分散处理，从而使预测可靠性、预测精度得到进一步提升。不同模型的模型系数会随着时间变化发生相应改变，同固定权值集成预测相比，利用单个动态变化的权值集成的独立预测模型，其适应性将更好。

2.3.1 降雨条件下的CA交通流模型

设定道路由N个元胞组成，长度为L。任何一个元胞在任意时刻的状态只有被占据或者无车两种；由于车辆长度和安全距离的影响，一辆车可以占据多个元胞。第i辆车的速度vi（i=0,1,2…vmax），其中vmax为车辆最大期望速度，设定每个时间步长为1s。本文的研究仅仅针对小客车，同时，设定每辆车的最大期望速度和制动减速均为一样。

在构建的模型中，车辆有三种状态：

1）两车间距远远大于安全距离，车辆进行加速，直至达到最大期望速度；

2）行驶过程中的车辆速度依赖于前方车辆的速度以及和前方车辆的距离，要保证安全的行车距离，以此进行速度的调节；

3）当两车间距不断缩小，驾驶员要减速保证安全。

降雨条件下对交通流的直接影响是车辆速度降低、车辆距离增加，因此，该模型引入一些参数：

β：降雨条件下的速度参数，取值0～1之间；

βi·vmax：i种降雨条件下的最大期望速度；

α：降雨条件下的间距参数，取值大于1；

α·ds：i种降雨条件下最小安全距离；

Ls：可视距离。

具体演化规则如下：

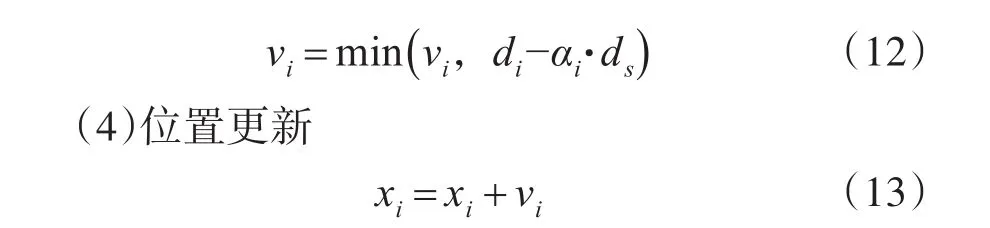
其中，vi为当前车辆i的速度；di为当前车i与前车间距；vmax为最大期望速度；ds为最小安全距离；xi为当前车i的位置。

2.3.2 组合预测模型算法

假定在分析、研究某一问题的过程中，设计创造了n种预测方式，那么此问题之中，某变量的N个实际观测值则具体为Yt(t=1,2…,N)，t为观测时间。设集成预测方法的权值系数向量为W=，其中wi为第i种预测方法在集成预测模型中的权值系数，有假定第i种预测方式的预测值利用 fit进行表示，那么集成预测模型的预测 ft则可以利用式（14）进行表示，具体为

设元胞自动机模型在t时刻的预测值为L（t），GM（1，1）模 型 在 t时 刻 的 预 测 值 为 G（t），t=1,2,…n。根据式（14）得出两种模型集成的表达式为

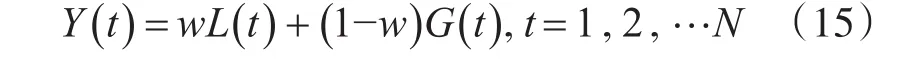
Y(t)为利用动态权值将元胞自动机和GM（1，1）模型的预测值进行累加所得的具体预测结果，其中w为动态权值，t为该预测数值产生的时间。

结合实际情况，求出最佳权值系数是实现模型集成的重要前提与基础，本文的权值w则是在0～1之间所选取的11个数值。通过对图1进行观察与分析，了解集成两种模型预测结果的详细流程与步骤，具体为

Step1：从t=1时刻开始，分别将两种模型的预测结果和各自权值系数w进行乘积处理；

Step2：把Step1中两种模型乘积处理后的预测结果进行叠加，然后求得经过加权处理之后的时间点t具体预测结果；

Step3：重复Step1的流程，直至全部预测时间点的预测值均利用权值集成。

根据图1中的步骤进行循环计算与分析，共对外输出11组同权值w存在密切关联的数据，从而获得一组经加权集成处理之后的交通流预测数据，如式（16）所示：

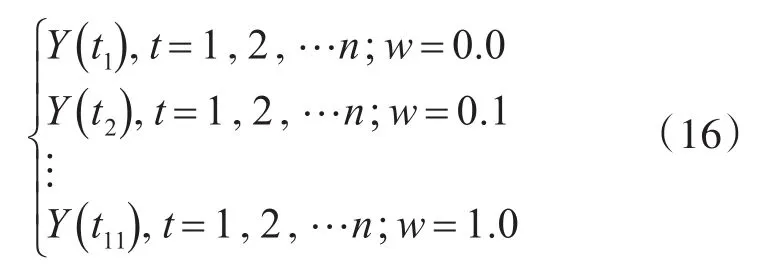
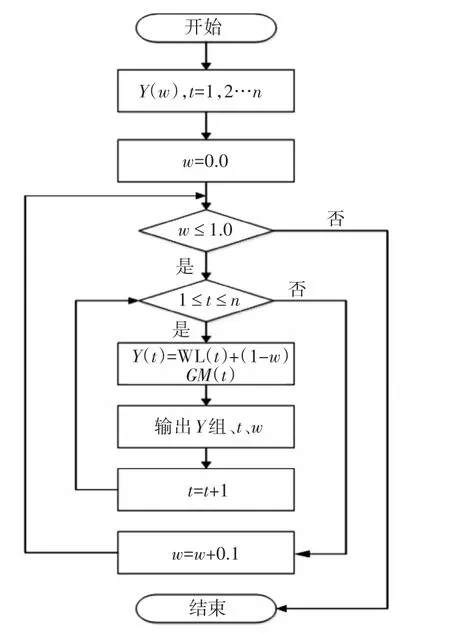
图1 元胞自动机和GM（1，1）模型组合过程

为了更加方便、快捷地明确权值w，本文引入关联度概念。若因素或者事物变化的大小、趋势十分相似，那么认定二者间存在较强的关联度，若与此相反，则表明关联度比较弱。本文以预测交通流曲线、实际交通流曲线二者形状的相似度表示关联度。若二者的形状逐渐趋近，那么表明二者的关联度较强，若曲线形状差别比较大，那么两者间存在的关联度比较弱。所以，对关联度进行评判时，可以将实际值曲线、组合模型预测值曲线形状的相似度作为衡量标准。基于此，求得11组预测数据的实际值、组合模型预测值的关联度，并结合实际情况，选出关联度最大的预测数据，然后匹配相对应的权值，求出具体的预测结果。对关联度进行分析运算的过程中，可以参照式（17）：

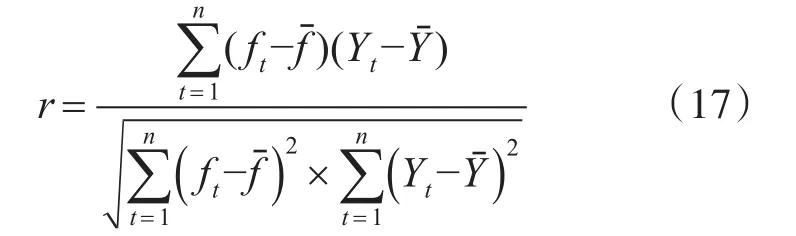
由于GM（l，l）属于特殊的动态模型，其处于一种动态变化之中，为保证权值系数的动态步调与GM（1，1）模型保持同步，当GM（1，1）的参数产生变化之后，需要借助EViews数据分析器进行再次分析运算，并得出新的权值系数。通过对11组实际值和组合模型预测值的关联度全方位、多层面的研究分析，可以得到图2的结果（横轴为关联系数r，纵轴为权值系数w）。

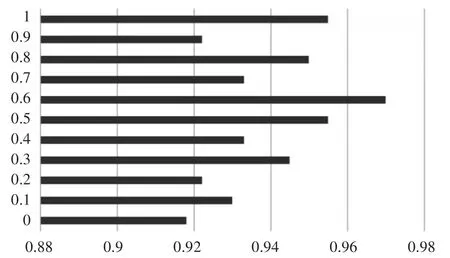
图2 权值系数w对应的关联系数r的值

通过对图2分析可知，当权值系数w为0.6时，实际值、组合模型预测值的关联度最大，集成预测精度最高。因此，可以将组合预测模型的权值系数确定为0.6。

3 实验与结果分析

3.1 天气样本抽取

为了全面、深入地掌握交通流预测过程中天气对其产生的影响程度，本文实验数据采用某城市交通检测数据，每间隔1min系统进行检测线圈数据采集。

数据集被细化为两大部分，其一是训练数据集；其二是预测数据集。鉴于冰雪和不同能见度的气象条件与雨天条件类似，且天气数据较少，实验数据较难获取，因此本次实验选择了雨天、晴天这两种状况作为研究对象。对于晴天模式，选取数据的时间范围为2017年11月2日～18日，训练集中共包括9395组数据，其中11月19日的数据，预测集共包含697组信息数据。对于雨天模式，选取数据的时间范围为12月8日～16日，训练集共包含3763组信息数据，其中12月17日的预测集共包含593组信息数据。

3.2 评价指标

本文引进两个评价预测拟合度指标来进一步提高预测的精度，通过把预测值与真实值进行对比分析，从而判断预测方式是否合理。

1）平均平方误差（MSE），主要是指实际数值、预测结果之间差值平方的算数平均数值：

2）平均绝对百分比误差（MAPE），指实际测量值、预测数值之间的差值占实测数值百分比的算术平均数值：

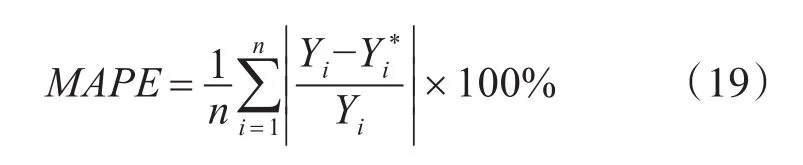
上述公式之中，n、Y*i、Yi分别表示样本数、预测值、实际值，平均平方误差可以真实、充分、全面地展现预测精度，但是无偏性的衡量比较困难。而平均绝对百分比误差则可以对预测模型的无偏性进行精准衡量，与平均绝对偏差进行配合应用，则可以实现良好互补，能够真实全面、详细、客观地评价真实数据、交通流预测的拟合度。

3.3 结果及分析

图3所示是基于气象条件改进的CA和GM（1，1）组合交通流预测模型与单个模型预测结果和实际值的折现对比图（横轴为时间/min，纵轴为交通流量/辆）。

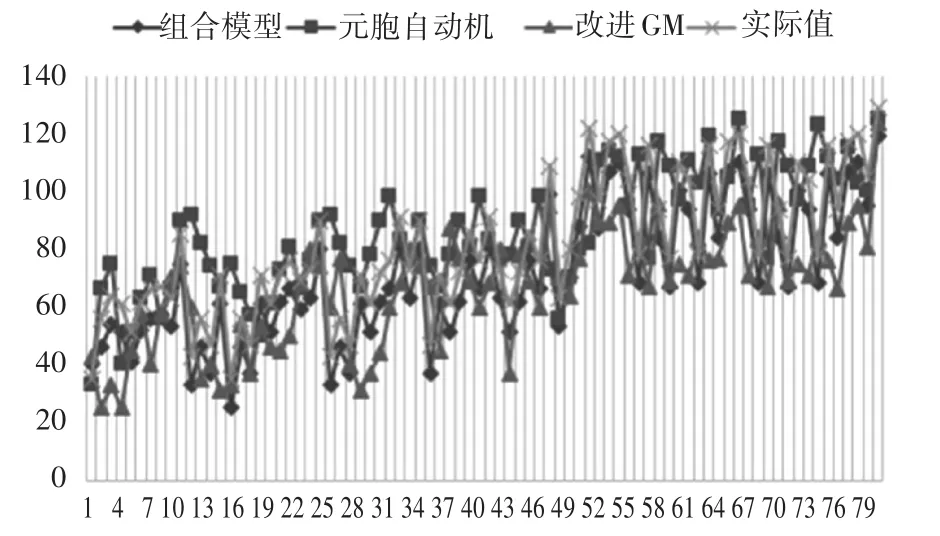
图3 组合模型与单个模型的预测对比图

由图3可以看出，组合模型相比单个模型预测值更趋近于实际值，仅存在微小差别。结合实际情况，分别求出实际值、预测值的MAPE及MSE对比如表1所示。结果显示，从MAPE或者是MSE指标上，相对于单个模型，改进后的组合模型预测方法虽然提高较小，但均有所改善。其中，MAPE值分别减少0.19%、0.55%，MSE值分别减少18.35、42.78，训练时间也分别减少0.25s、1.79s。因此，基于气象条件改进的CA和GM（1，1）组合交通流预测模型对于交通流量的预测情况较为理想，与单个模型相比较也具有一定优势。

表1 组合模型与单个模型性能比较

4 结语

本文提出一种基于气象条件改进的CA和GM（1，1）组合交通流预测模型。首先针对气象条件带来的影响，引入了一些参数，更新了演化规则，然后将改进后的元胞自动机预测模型和灰色理论GM（1，1）预测模型进行组合。经实验验证，组合交通流预测模型对于交通流量的预测情况较为理想，与单个模型相比较也具有一定优势。由于冰雪和不同能见度的气象条件实验数据较难获取，本文仅针对降雨条件进行了实验论证，因此今后的研究工作将会补充其他气象条件的数据和实验，进一步完善预测模型。