一种适用于多功能相控阵雷达的姿态补偿方法∗

傅虹景 薛俊杰 于守江 劳丹涤 罗 静

（上海航天电子技术研究所 上海 201109）

1 引言

多功能相控阵雷达在行进间工作中，受路面平整度或气候的影响，载体平台会产生横滚纵摇的晃动，导致雷达波束的实际指向偏离理论指向，进而使得雷达测量目标的方位角与俯仰角存在误差［1～3］。为满足雷达跟踪目标精度的性能，需要补偿载体横滚纵摇所引起的测角误差［4～5］。传统方法通过采用机械稳定平台来克服载体的晃动，保证雷达处于近似水平的状态，但是存在控制精度差，造价昂贵等缺点，未能广泛地应用［6～7］。现在，通常采用在雷达数据处理中进行姿态补偿，来减小载体晃动的影响，包括对接收点迹的补偿和发射波束指向的补偿［8～9］。

本文首先介绍了雷达系统所用的不同坐标系定义和坐标变换公式，然后提出一种适用于多功能相控阵雷达的姿态补偿方法，该方法推导了姿态补偿中坐标变换的公式，给出了多功能相控阵雷达的姿态补偿的处理流程。最后根据某多功能相控阵雷达的试验结果，验证了本方法的正确性。

2 坐标系定义

2.1 北东天大地坐标系

北东天大地坐标系如图1所示，其原点O为雷达天线的质心，X轴为水平面内指北方向，Y轴为水平面内指东方向，Z轴垂直于水平面指天方向［10～11］。雷达的点迹测量值通常由极坐标表示，方位角a为目标在水平面的投影与X轴的夹角，俯仰角e为目标与水平面的夹角，距离r为目标与雷达的径向距离。目标在直角坐标系的位置为(x ,y,z)和极坐标系下的位置为(r , a,e)，其转换关系可以表示为

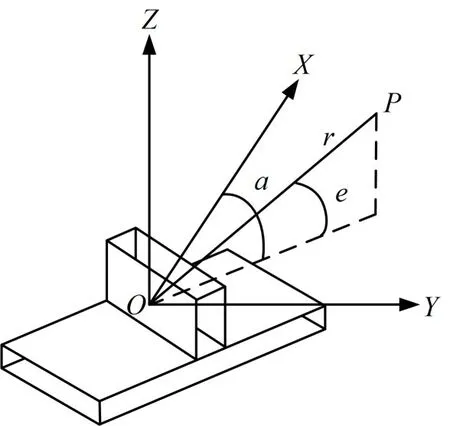
图1 北东天大地坐标系

2.2 载体坐标系

载体坐标系如图2所示，其原点O为雷达天线的质心，X轴为载体前进方向，Y轴为载体右侧方向，Z轴垂直于载体水平面指天方向［12～13］。在载体坐标系中，可以直观地看出载体平台水平面变化对雷达测量精度的影响。

图2 载体坐标系

2.3 坐标变换

载体平台的晃动会使得载体坐标系的坐标轴方向发生变化，即坐标系的旋转变换［14～15］。简单的坐标旋转变换如图3所示，OX和OY绕OZ轴逆时针旋转θ角，得到OX′和OY′，即坐标系OXYZ逆时针旋转得到了坐标系OX′Y′Z。假设坐标系OXYZ有一点P，其坐标可以表示为X=[x ,y,z]′，那么在坐标系OX′Y′Z下，表示为 X1=[x′, y′,z′]′。根据几何关系，两个坐标系下的坐标变换公式为

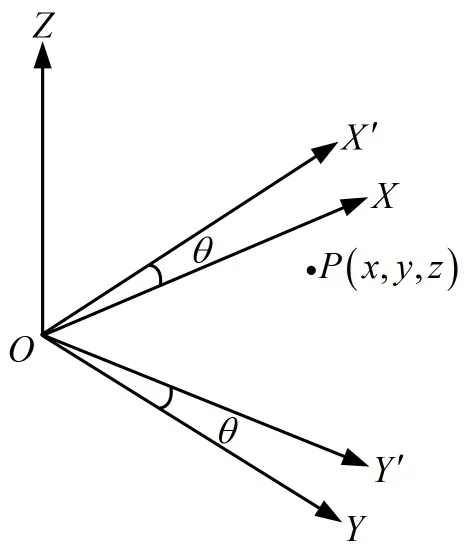
图3 坐标系旋转变换

式中：L1为绕Z轴的基本旋转矩阵［16］：

同理，绕X轴逆时针旋转的基本旋转矩阵和绕Y轴逆时针旋转的基本旋转矩阵为

任何坐标系的旋转变换可以由基本旋转矩阵合成得到［17］。

3 多功能相控阵雷达姿态补偿方法

3.1 姿态数据的获取

在雷达系统中，载体姿态数据是由导航系统提供的，包括横滚角α、纵摇角β和载体北向角γ，其定义如下。

1）横滚角：载体坐标系中，OY和OZ沿OX轴旋转的角度，即当载体晃动时，载体平面与水平面在Y轴方向的夹角，以逆时针为正，即载体右侧低时为正［18］。

2）纵摇角：载体坐标系中，OX和OZ沿OY轴旋转的角度，即当载体晃动时，载体平面与水平面在X轴方向的夹角，以逆时针为正，即载体上仰时为正［19］。

3）载体北向角：载体坐标系中，OX轴与正北方向的夹角，以顺时针为正［20］。

雷达系统获取姿态数据的原理如图4所示，雷达接口控制模块接收导航系统发出的姿态数据，并标记时戳，将打包后的姿态数据送与雷达数据处理，雷达数据处理将姿态数据按时间顺序缓存至队列。同样的，雷达信号处理模块处理雷达回波，形成点迹，并标记时戳，将打包后的点迹数据送与雷达数据处理。

图4 雷达接收点迹与姿态数据流程图

3.2 点迹姿态补偿

雷达在行进间工作时，受载体平台晃动的影响，获得的点迹测量值是非稳定坐标系下的目标位置，所以需要根据姿态数据，转换到稳定坐标系下，从而保证对目标的精确跟踪。雷达点迹补偿的方法如图5所示，具体步骤如下。

图5 雷达点迹姿态补偿流程图

1）查找点迹对应的姿态数据

在雷达行进间工作时，姿态数据是时变的，只有准确找到获取点迹时对应的姿态数据，才能保证补偿的正确性。雷达的点迹数据和姿态数据都有时戳标记，且该时戳标记是同源的，所以可以根据时间查找点迹对应姿态数据。假设姿态数据队列中第k个数据为Pk=[αk,βk,γk] ，对应的时间为tp(k)。假设获取点迹的时刻为td，由于姿态数据是按时间排序的离散队列，很难保证存在tp(k)=td的姿态数据。因此，需要找到满足式（6）的两个相邻的姿态数据：

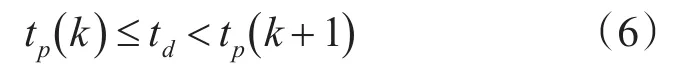
通过时间差对相邻的姿态数据加权，可以得到td时刻点迹对应的姿态数据Ptd：

2）非稳定大地坐标系点迹转换到非稳定载体坐标系

由于横滚角和纵摇角的定义是在载体坐标系下的，所以需要在载体坐标系下进行姿态补偿。假设非稳定大地坐标系下的点迹数据为Xnsg=[xnsg,ynsg,znsg]′，将非稳定大地坐标系沿OZ轴顺时针旋转一个北向角，可以得到非稳定载体坐标系下的点迹数据Xnsc=[xnsc,ynsc,znsc]′，变换公式为

3）非稳定载体坐标系下点迹姿态补偿

横滚角和纵摇角两个变量的耦合作用使得姿态补偿有很大的复杂性，所以通常采用分步变换的方式，即每次变换只考虑其中一个参数发生变化。将非稳定载体坐标系先沿OX轴顺时针旋转一个横滚角，再沿OY轴顺时针旋转一个纵摇角，可以得到稳定载体坐标系下的点迹数据Xsc=[xsc,ysc,zsc]′［21］，变换公式为

4）稳定载体坐标系点迹转换到稳定大地坐标系

综上所述，根据式（8）、式（9）和式（10）可以得到点迹姿态补偿的变换公式：

由于雷达点迹的测量值通常是在极坐标系下的位置，所以将式（11）代入到式（1）中，得到点迹在极坐标系下的姿态补偿的变换公式。

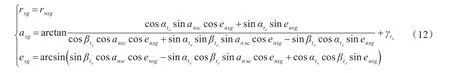
式中，ansc是非稳定载体坐标系下的方位角

根据式（12）可知，雷达在进行间工作时，会影响点迹测量值的方位角和俯仰角，对距离没有影响。

3.3 波束指向姿态补偿

多功能相控阵雷达对目标进行跟踪时，需要调度波束指向目标所在位置。当横滚纵摇角度较大时，存在波束可能覆盖不到目标的问题。所以，在雷达调度波束时，需要根据当前载体的姿态，来补偿波束指向，保证真实的波束可以覆盖目标，进而才能稳定跟踪目标。雷达波束指向补偿的方法如图6所示，具体步骤如下。

1）稳定大地坐标系波束指向转换到稳定载体坐标系

由于在调度波束时，该波束在下一调度周期才会发射，而下一调度周期载体的姿态数据是未知的。因此，选择当前时间最新的姿态数据Ptn近似作为下一调度周期的姿态数据。假设稳定大地坐标系下波束需要指向目标的位置为Ysg=[xsg,ysg,zsg]′，那么将稳定大地坐标系沿OZ轴顺时针旋转一个北向角，可以得到稳定载体坐标下的波束指向，变换公式为

2）稳定载体坐标系下波束指向姿态补偿

将稳定载体坐标系先沿OY轴逆时针旋转一个纵摇角，再沿OX轴逆时针旋转一个横滚角，可以得到非稳定载体坐标系下的波束指向Ynsc=[xnsc,ynsc,znsc]′，变换公式为

3）非稳定载体坐标系波束指向转换到非稳定大地坐标系

雷达调度的波束指向是大地坐标系下的，所以，将非稳定载体坐标系沿OZ轴逆时针旋转一个北向角，可以得到非稳定大地坐标系下的波束指向，变换公式为

综上所述，根据式（14）、（15）和（16）可以得到波束指向的姿态补偿的变换公式：

由式（17）可知，波束指向的姿态补偿近似是点迹姿态补偿的逆过程。将式（17）代入到式（1）中，得到波束指向在极坐标系下的姿态补偿的变换公式：

式中，asc是稳定载体坐标系下的方位角

4 试验结果分析

在某多功能相控阵雷达的试验中，目标飞行轨迹如图7所示，雷达在进行间对目标进行搜索和跟踪。图8给出了雷达在跟踪目标过程中，载体姿态数据的变化曲线，图9和图10给出了雷达对目标跟踪结果在姿态补偿前后与目标真值相比较的角度均方根误差，表1给出了雷达跟踪结果的平均均方根误差。

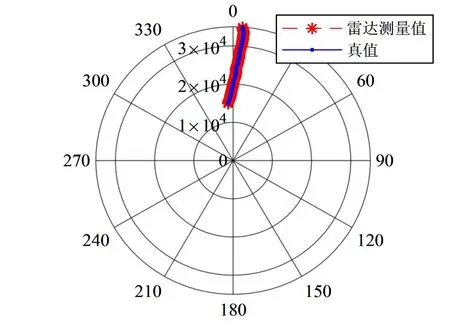
图7 目标运动轨迹

图8 载体姿态数据变化曲线

图9 方位均方根误差

由图8可知，雷达在行进间工作时，载体是处于非平稳状态，横滚角、纵摇角和北向角均是时变的，如果不进行姿态补偿，则雷达对目标的跟踪会存在误差，难以保证跟踪精度。从图9、图10和表1中可以看出，姿态补偿前的雷达跟踪结果的误差较大，其方位平均误差为0.55°，俯仰平均均方根误差为1.40°，已不满足雷达的精度要求。在姿态补偿后，雷达的跟踪结果误差有着显著的改善，其方位平均均方根误差为0.10°，方位精度提高了81.8%，俯仰平均均方根误差为0.11°，俯仰精度提高了92.1%，保证了雷达系统的跟踪精度要求。

表1 姿态补偿前后雷达精度对比

5 结语

本文提出的多功能相控阵雷达的姿态补偿方法主要解决雷达在行进间工作时，受载体平台晃动的影响，雷达的点迹测量值和波束指向存在角度误差，难以保证雷达精度的问题。该方法根据坐标系旋转变换的原理，通过将姿态数据解耦合，分步实现点迹测量值和波束指向的姿态补偿。同时给出了雷达接收点迹和姿态数据的流程，并提出了一种基于时间差加权匹配点迹对应姿态数据的方法。根据某多功能相控阵雷达的试验结果分析，通过该方法进行姿态补偿后，可以提高对目标的跟踪精度。