基于CFD的风电机组机舱传递函数数值模拟

王杲展，端和平，姜婷婷，罗勇水

(1.浙江运达风电股份有限公司，浙江 杭州 310012；2.浙江省风力发电技术重点实验室，浙江 杭州 310012)

0 引言

随着风电行业的发展，风电市场的成熟，对风力机组控制策略、运行发电量预警以及后评估的准确性提出了更高的要求。风轮前方轮毂高度的自由来流风速是以上过程中最重要数据之一[1]。在IEC标准《61400-12-1：2005》中利用气象桅杆得到自由来流风速[2]，但受限于气象桅杆的数量及成本问题。对此，IEC标准《61400-12-2：2013》中提到采用机舱传递函数来将安装在机舱上方的风速风向仪数据转化为机组前方来流速度，该函数是通过测风塔和风速风向仪的大量数据拟合得到[3-4]。在此基础上St Martin C M等人研究了复杂流动下风速风向仪测量的准确性与修正方法[5]。但以上通过样机测试得到的机舱传递函数局限于测试场地的条件，无法准确应用于所有风速区间或者其他环境条件下的工况。范奇等人在研究风电机组出力特性时，基于能量守恒建立机舱传递函数[6]。该方法无法考虑机舱外型对传递函数的影响。谢贤彬则利用激光雷达直接测试机组前方的来流情况，能保证测得数据的准确性，但存在成本问题且易受天气干扰难以应用到每台机组[7]。

基于数值方法模拟机舱附近的流动情况，建立机舱传递函数具备经济性及通用性。Sorensen J N 等人用致动线模型研究了风机的尾流特性[8]，Smaili A 和Masson C等人利用致动盘模型仿真机舱附近流场，研究了叶轮与机舱的相互作用，分析了自由来流风速与机舱附近风速的关系，并认为该关系能用于在机舱上布置风速风向仪[9-10]。Ameur K 等人研究了二维和三维的风机模型，量化了机舱外形对风速风向仪测量结果的影响[11]。但上述研究未考虑机组在来流风速增大后会进行变桨控制，变桨后机组模型发生改变对机舱传递函数的影响。

为更深入研究数值模拟在机舱传递函数方面的应用，以某2.0 MW风机为研究对象，在Fluent平台上建立全尺寸模型并进行仿真[12]，利用2.0 MW测试数据进行模型可靠性验证，结合2.5 MW机组仿真结果研究不同来流风速对机舱传递函数的影响，改变2.0 MW机组桨距角并重新建模，探讨了桨距角改变后机舱传递函数所发生的变化。

1 机组几何建模

以有测试数据的2.0 MW风电机组为实例，为模拟真实的运行情况，建立全尺寸几何模型。考虑几何的复杂性和后续网格划分的复杂程度，删除风速风向仪支架及塔筒，忽略机舱及导流罩内所有结构，忽略壁面厚度，只考虑机组外形对流动的影响。机组各项模型参数如表1所示，模型整体外形如图1所示。

表1 模型参数

图1 风机几何外形

2 网格模型划分

计算域离散时考虑叶片的旋转运动，建立旋转域与静止域，旋转域为包含桨叶以及导流罩的圆柱状，静止域为包含机舱的长方体外流场域，为使计算域边界不受机组运行流动的影响，准确代表自由来流或者出流的情况，静止域范围分别取机组前方4D、后方10D、上左右侧各2.5D，底部为实际高度，计算域如图2所示。

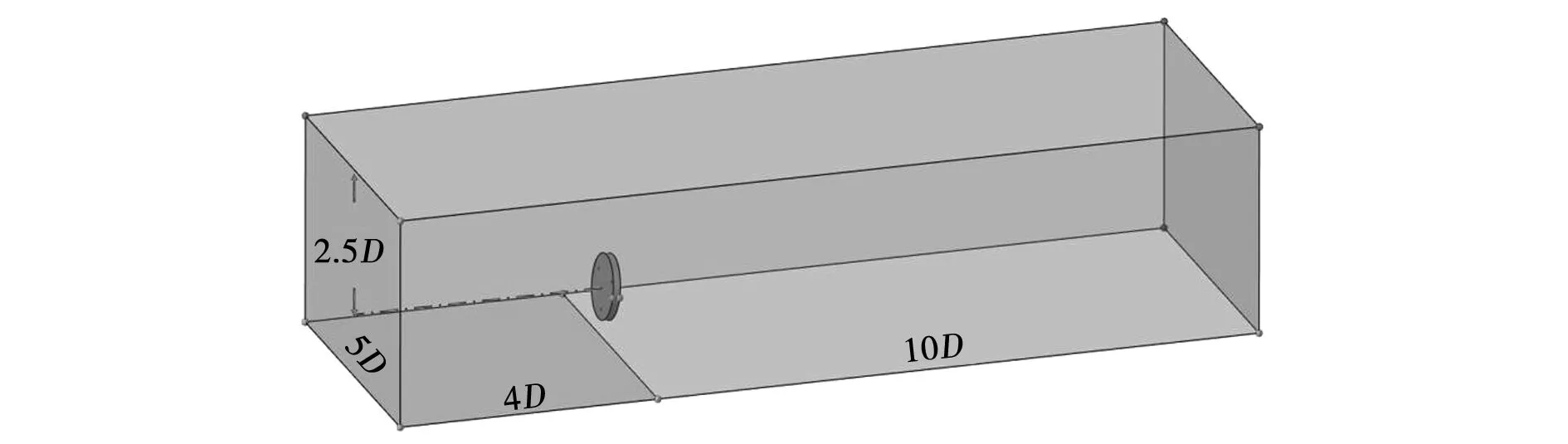
图2 流场计算域

机组网格划分全部采用非结构网格，其对轮毂、机舱和叶片表面状况以及部件连接处有更好适应性。其中旋转域全部为四面体网格，静止域主要为六面体网格，为更准确捕捉风速风向仪周边的流动情况，在机舱、轮毂和叶片根部采用64 mm的网格尺寸，同时在机舱上方部署一个加密区域，整个模型网格数量约为700 W，网格示意如图3、图4所示。

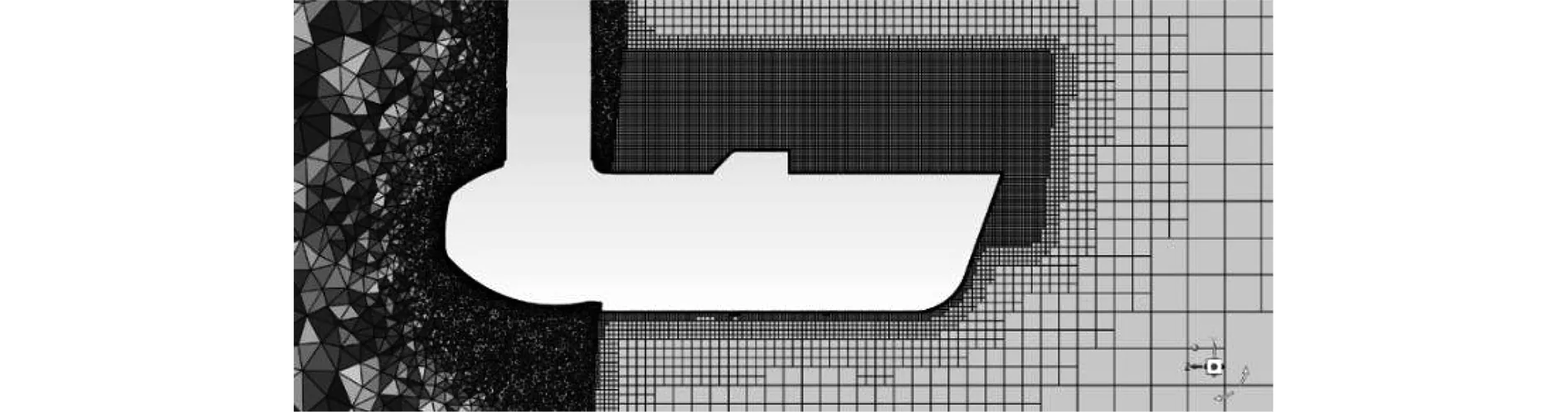
图3 XZ截面网格

图4 局部网格

3 仿真模型

叶片的旋转运动使用MRF(多重坐标系法)模型体现，在旋转域中单独设定坐标系与旋转速度。由于叶片所处的不同方位角对流场影响显著，选用4种(如图5所示)具有代表意义的方位角来模拟整个旋转周期内叶片尾流对风速风向仪处的实际影响，其余边界条件见表2。

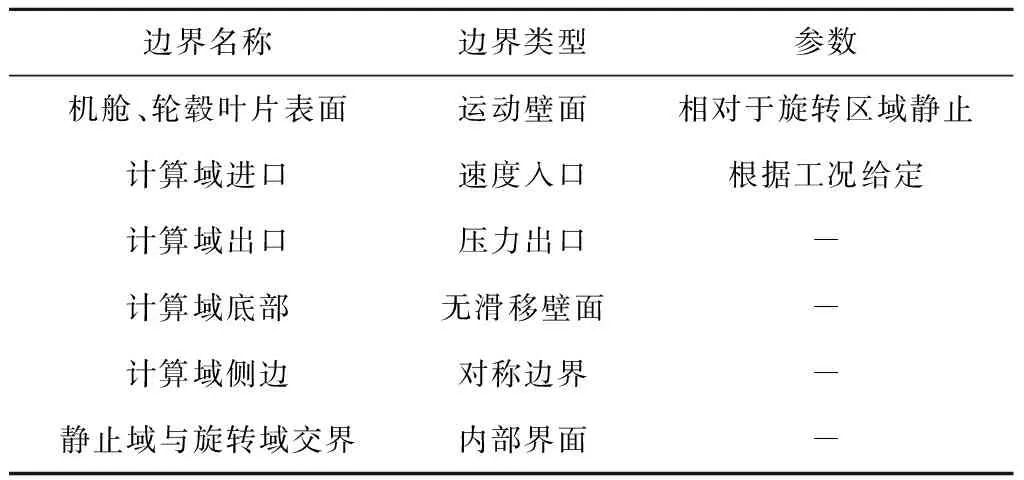
表2 边界条件

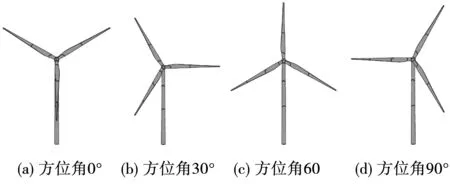
图5 机组不同方位角示意图

机舱传递函数是基于机舱上方的尾流流场研究得到，因此选用合适的湍流模型对该研究较为重要，根据文献以及相关领域的应用，对SSTk-ω模型以及Standardk-e模型进行对比，以上两模型均为两方程模型，主要差异是对壁面函数的处理。用Simple算法进行压力速度耦合，压力项离散为标准，其余均为二阶迎风格式。

验证对比采用2.0 MW机组的8 m/s来流工况，对不同方位角风速仪仿真速度计算结果进行比较，结果为4个方位角平均得到，结果如表3所示。其中Standardk-e模型的计算结果误差好于SSTk-ω模型，后续计算均采用Standardk-e湍流模型。

数值模型受网格影响较大，为论证网格无关性，增加一组机舱、轮毂和叶片根部分别采用32 mm网格尺寸，总数约为2 400 W的模型进行计算，同样采用2.0 MW机型的来流8 m/s工况，对比结果如表4所示，误差均在1%以内，说明700万尺度的网格模型已经满足计算条件，结果不再受到网格的影响，后续均采用该网格尺度进行划分。

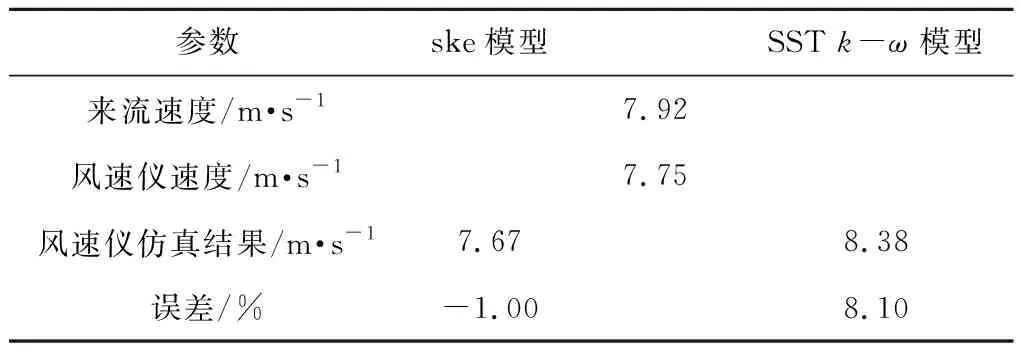
表3 不同湍流模型结果对比

表4 网格无关性验证结果

4 仿真验证及分析

4.1 模型验证

该数值模拟用于建立机舱传递函数，机舱附近速度场为评价模型可靠性的重要指标，采用风速风向仪所处位置的速度进行模型验证，验证示例为2.0 MW机组。

测试数据由机组功率曲线测试得到，测风塔风速视为来流风速，对原始数据进行扇区以及设备冰冻等条件筛选后得到对应的测风塔风速以及风速仪实测风速，仿真计算时对4个不同方位角的结果进行平均，监测点位置参考图1的实际风速仪安装位置取得，即图6中所标注的局部面，采用该局部面的平均值来体现此处流速。

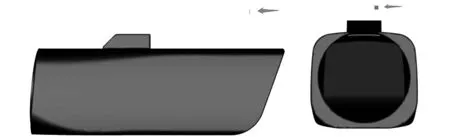
图6 风速监测点位置图

综合考虑仿真资源以及结果的可靠性，排除单个测试数据的测试偏差，取5个具备代表性的来流风速区间平均值进行仿真，与测试数据进行对比，结果如表5所示，风速仪实测风速与相应位置仿真风速误差控制在7%以下，风速值相差均在0.3 m/s以内，该误差在风电机组对发电量进行预警及后评估时可接受。

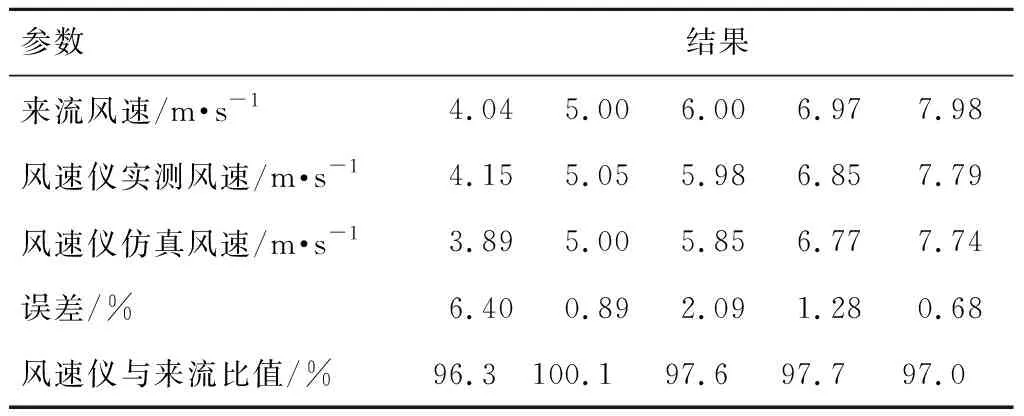
表5 2.0 MW机组仿真测试结果对比

以上对比说明利用非定常的数值模拟能准确得到机舱上方的速度场结果，证明了该模型以及数值方法的可靠性，并且通过速度场结果和来流风速，能建立相应的机舱传递函数。

4.2 结果分析

不同机型由于其机舱叶片外型的区别，尾流的范围以及特性存在差异，风场建设时考虑风资源的充分利用以及噪声等因素影响，往往会选择多种机型混搭的方式，针对不同机型给定相应机舱传递函数针对该情况，在保证网格划分以及仿真参数一致的情况下，对某2.5 MW机组进行模拟，取5个风速值进行计算，得到的风速结果如表6。

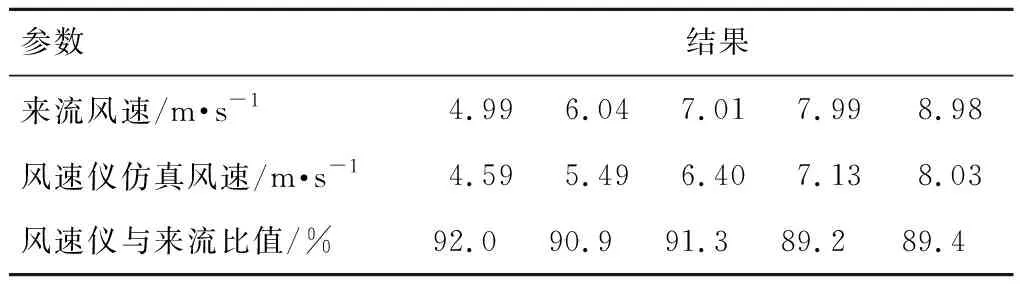
表6 2.5 MW机组仿真结果

根据两款机组的风速仪仿真数据与来流风速，拟合线性曲线，得出的机舱传递函数如下：

2.0 MW机组：y=1.039 8x-0.084 9

2.5 MW机组：y=1.164 3x-0.365 9

纵向对比两者的风速仪与来流速度比值，2.0 MW机组比值在97%左右，而2.5 MW机组比值在90%左右，说明不同机型的机舱传递函数存在较大差异，在风场实际应用中，有必要对不同机型给定对应的机舱传递函数。

横向对比不同风速段下的风速仪仿真风速与测风塔比值，发现当风速改变时，该比值不发生明显变化，说明当来流风速以及叶轮转速发生改变时，尾流对风速仪速度的影响也随之改变，但最终不影响机舱传递函数。

4.3 变桨影响分析

机组在实际运行时，随着来流风速的增大，机组会改变叶片桨距角，通过变桨来控制功率，当叶片桨距角发生改变时，所造成的尾流特性会发生改变，进而影响机舱传递函数。以2.0 MW机组为例，对其3°、6°、9°以及11°桨距角工况进行模拟，通过有限元仿真得到其对应的来流风速和叶片转速，不同桨距角模型如图7所示。

图7 不同桨距角局部模型

以上变桨工况结果见表7。

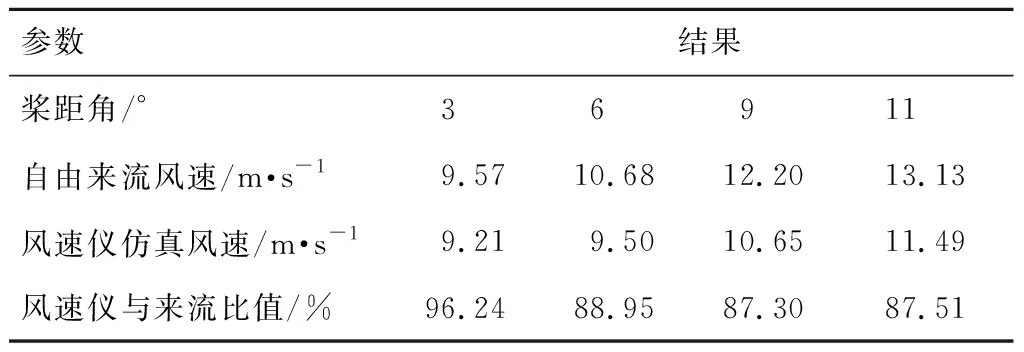
表7 不同桨距角模型仿真结果

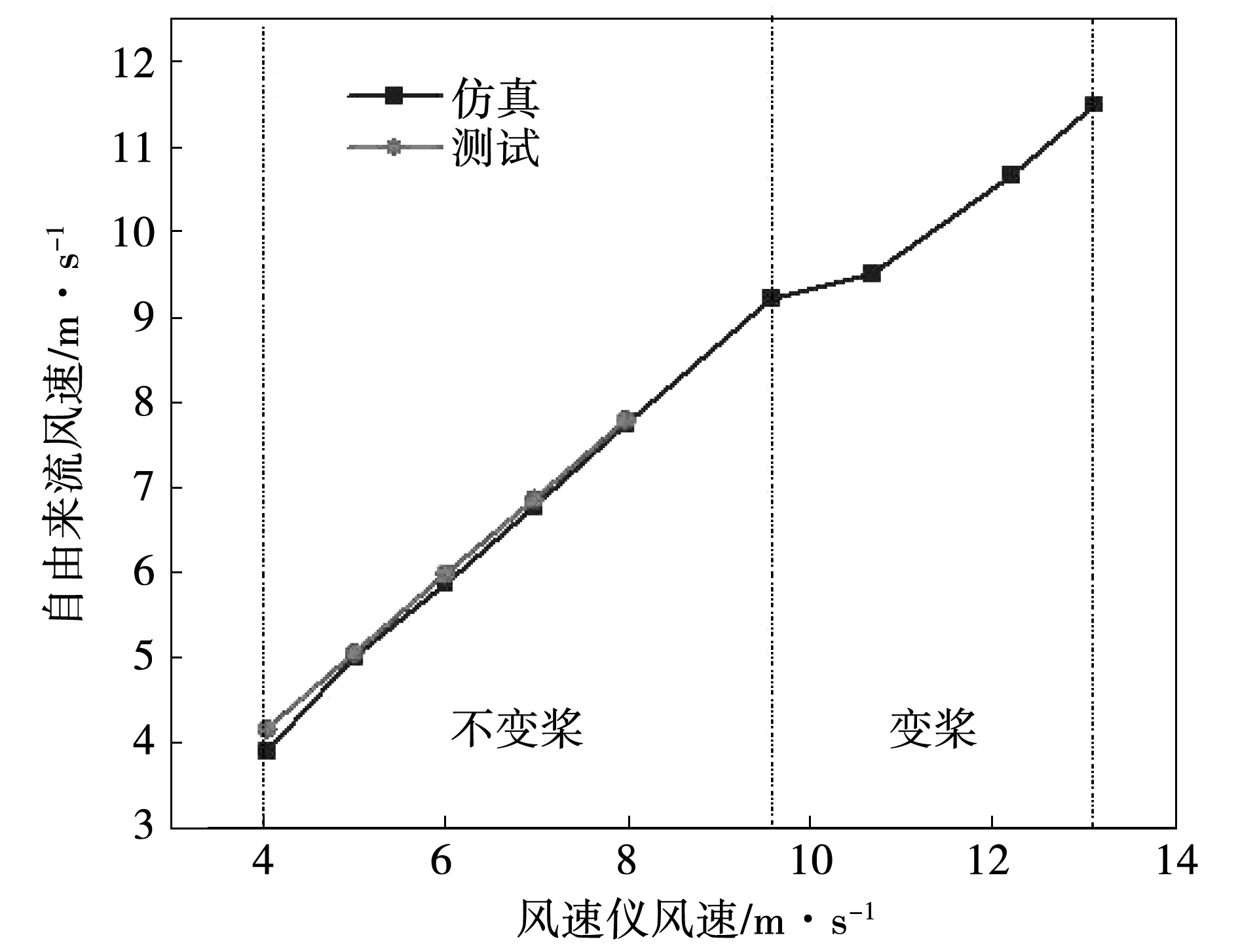
图8 各工况风速仪-自由来流风速

机组由于来流风速增大而进行变桨控制后，风速仪与来流风速比值发生了明显变化，以变桨后的4组数据拟合机舱传递函数，结果是：y=1.469 4x-3.614 3，与不发生变桨前的传递函数：y=1.039 8x-0.084 9不同，如果以不发生变桨的传递函数去计算变桨后的风速情况，将会存在12%的误差。

5 结论

以2.0 MW、2.5 MW机组为研究对象，建立基于Fluent的MRF模型对该机组4种方位角情况进行全尺寸流动稳态仿真，模拟了在叶片尾流影响下机舱上方流动情况，并利用2.0 MW机组的功率测试结果进行仿真验证，继而对2.5 MW机组以及2.0 MW各桨距角模型进行机舱传递函数仿真，得到以下结论：

(1)2.0 MW机组仿真结果与测试误差在0.3 m/s以内，非定常数值模型、仿真方法及相应参数设置能够对机组外流场，尤其是经过风轮之后的机舱上方流动情况进行较为准确的仿真模拟，可用于建立机组机舱传递函数；

(2)在额定风速前的各风速段下，同型号机组的风速仪测量速度与来流速度比值基本保持不变，能用同个机舱传递函数去应用；

(3)机组进行变桨后，模型的改变会引起流场的变化，机舱传递函数发生改变，风速仪与来流风速比值相比不发生变桨前偏小。