基于内积矩阵及卷积自编码器的螺栓松动状态监测

张敏照，王 乐，田鑫海

(西北工业大学航空学院航空结构工程系，陕西，西安，710072)

结构健康监测技术是指通过监测到的系统响应，并结合结构自身的特性，来确定结构的损伤位置，评估结构的损伤程度，预测结构的剩余寿命[1−4]。目前，基于振动的结构健康监测技术，尤其是飞行器结构健康监测，是国内外的一个研究热点[5]。

飞行器结构在服役过程中会遭遇各种环境载荷的作用[6−7]，从而导致其螺栓连接结构的预紧扭矩下降，螺栓发生松动甚至松脱，给飞行器结构带来了严重的安全隐患，因此亟待一种稳定可靠的方法对螺栓松动状态进行监测。詹阳磊等[8]对螺栓连接的铝板进行了温变工况下的实验，可以在一定程度下识别螺栓松动。杜飞等[9]利用透射过螺栓的超声导波信号的均方根偏差作为拧紧指标，对螺栓连接结构进行了松动监测。NA 等[10]使用机电阻抗技术和概率神经网络来识别螺栓结构试样上螺栓的扭矩损失。王刚等[11]利用铝板上的压电阵列采集Lamb 波信号，建立高斯混合模型来监测螺栓松动情况。TU 等[12]使用光纤布拉格光栅传感器来监控螺栓连接处在热负荷下的夹紧力变化。目前现有方法对螺栓松动监测的研究已经取得了丰硕的研究成果，但实际工程中构件所处环境复杂，可能会受到电磁干扰、温度变化等影响，由于传感器的灵敏度有限，构件中的一些状态变化反映到测试信号中时，信号变化通常并不明显。因此，对信号进行数据分析和损伤特征提取是螺栓松动监测的一个关键问题。

目前，基于信号处理的结构健康监测研究工作集中在如何利用先进的信号处理技术有效地进行信号降噪、结构损伤特征提取、辨识损伤位置上[13 −14]。徐浩等[15]引入二维连续小波变换与数据融合技术，增强了损伤检测模型的抗噪能力以及工程适用性。LU 等[16]提出了基于自适应谐波小波变换的方法，并使用时频分析技术来对波信号进行特征提取。周广东等[17]针对桥梁监测的无线测点优化布置问题，提出了一种基于自适应动态罚函数的改进广义遗传算法。在上述方法中，对参数优化的要求较高，这使得相关信号处理的结构健康监测方法依赖于工程师的经验，会造成不可避免的人为误差。同时，现有的研究方法大多是基于结构模型驱动的健康监测方法。然而，针对复杂结构的健康监测，难以建立准确的结构理论模型，限制了这些方法在结构健康监测领域的应用。同时，随着监测技术手段的不断提高，结构健康监测领域产生了海量的监测数据。因此，有必要设计基于数据驱动的结构健康监测方法来对结构的螺栓松动进行监测。

近年来，深度学习技术，如堆栈自动编码器(stack autoencoder, SAE)、卷积神经网络(convolutional neural network, CNN)、胶 囊 网 络(capsule network, CapsNet)、卷 积 自 编 码 器(convolutional autoencoder, CAE)等已经成功应用到信号处理和结构健康监测领域。与现有的基于模型驱动的方法相比，基于数据驱动的方法，如基于深度学习的损伤特征提取技术可以自动从被测信号中提取到有用的损伤特征，从而避免了人工选择参数带来的误差。例如，KANARACHOS 等[18]结合小波变换、神经网络和希尔伯特变换提出了一种新的信号处理算法；CHANG 等[19]提出了一种基于神经网络的结构健康监测方法，可用于估计刚度降低引起的损伤；CHEN 等[20]提出了一种智能、端到端的健康指标构建方法，该方法通过递归神经网络连接顺序局部特征，使递归层中提取的特征包含具有时间序列的全局信息；DENG 等[21]将空洞空间金字塔池化模块设计为桥梁损伤检测的新型网络，提出了一种桥梁结构损伤检测模型。上述方法在神经网络训练过程中学习和提取输入数据的特征并进行结构的损伤检测。但是针对大量损伤特征不明显、噪声比较大的数据，简单的利用神经网络可能无法提取到完整的损伤信息。

为了克服已有健康监测方法在信号处理和特征提取问题上的不足，本文提出基于内积矩阵的卷积自编码器深度学习框架。首先，通过实验测得的响应数据求得内积矩阵，组成模型的训练数据集。其次，通过神经网络学习训练数据的重要特征，并调整计算内积矩阵时的采样点数和CAE 网络的批次大小等参数，以得到更加合适的网络模型。然后，将内积矩阵数据作为网络的输入，将标签即预紧扭矩作为输出，从而进行螺栓松动状态的监测。最后，与使用 IPM 的CNN、SAE、CapsNet(即 IPM-CNN 、IPM-SAE 和IPMCapsNet)相比，IPM-CAE 获得了最佳的训练效率和最优的监测准确率，验证了所提方法在螺栓松动状态监测上的优势。

首先，介绍内积矩阵的概念；然后，简述卷积自编码器的理论基础；最后，提出基于内积矩阵及卷积自编码器的螺栓预紧扭矩监测方法。

1 理论基础

1.1 基于内积矩阵的振动信号处理方法

假定在白噪声激励下，采集获得结构上若干测点1,2,···p上的加速度响应为x¨1,x¨2···,x¨p，参考点的加速度响应为x¨j，各响应的采样点个数均为Ns，可以获得内积向量的计算公式如下[22]：

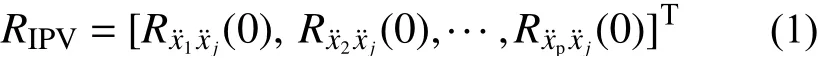
式 中，Rx¨px¨j(0) 表 示 响 应x¨p(t)(p=0,1,···n)与 响 应¨xj(t)的互相关函数在时间延迟为零的值。根据线性系统的叠加原理可知，针对某一参考点，通过相关理论推导，可以确定内积向量为结构各阶模态振型的线性组合。结构发生损伤时模态振型的变化可以体现在内积向量的变化上。内积向量是由结构加速度响应测点的时域响应直接计算得到的，此过程不需要模态识别，从而有效避免了模态识别带来的误差。因此，内积向量可以有效地应用在结构损伤识别中。

由于内积向量是一个一维向量，包含的结构测点的时域响应数据较少，且在深度学习神经网络模型中需要输入的数据通常为二维矩阵，因此，为了充分利用实验中各测点的时域响应数据并满足神经网络的输入要求，可将内积向量扩展到内积矩阵。在内积向量中，仅采用某一个测点j的加速度响应作为参考点来与其他响应进行内积运算。在内积矩阵的计算中，将参考点j的取值分别设为各个测点，即j=1,2,···p，则内积矩阵的计算公式如下：

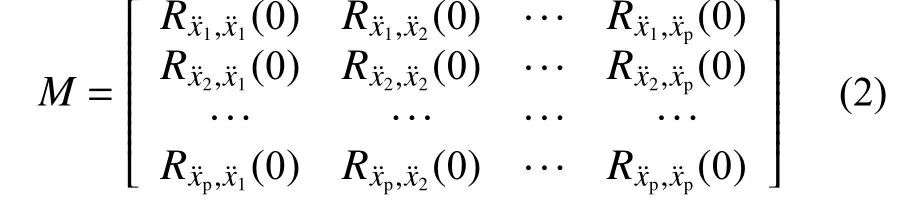
1.2 卷积自编码器

卷积自编码器使用了传统自编码器的无监督学习方式，并结合了卷积神经网络的卷积和池化操作，从而实现特征提取[23]。卷积自编码器在其训练过程中，先对输入数据进行编码再解码，并比较解码后的数据与原始数据的差异进行训练，从而得到比较稳定的参数。在一层的参数都训练好后，再进行下一步的训练。在卷积自编码器中，使用卷积神经网络作为编码器和解码器，从而对数据进行特征提取。简单的卷积自编码器如图1 所示。

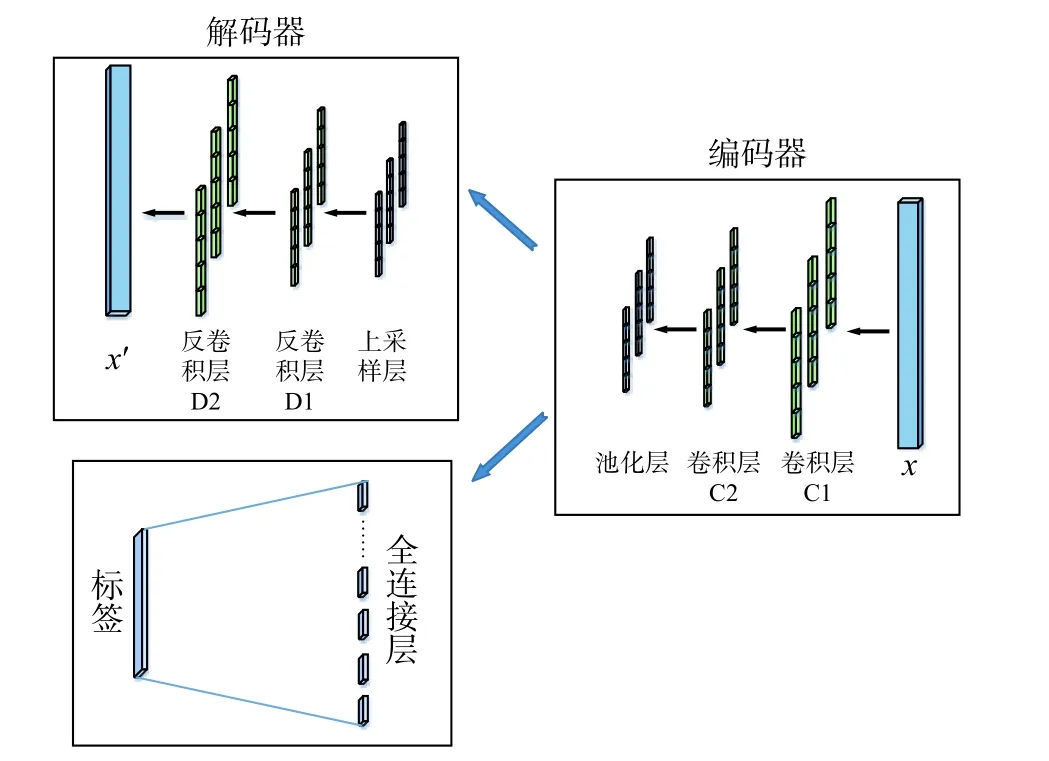
图1 CAE 网络结构Fig. 1 Network structure of CAE

卷积自编码器的原理如下：

在卷积层中，假设有k个卷积核，每个卷积核由参数wk和偏置bk组成。用hk表示卷积层，输入x后可生成k个特征数据，则：

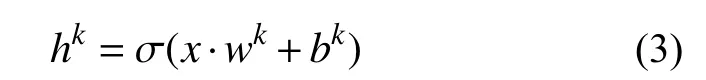
在池化层中对卷积层生成的特征数据进行池化操作。

然后，对上面生成的特征数据进行反池化操作，使用保留池化时的位置关系矩阵，将数据还原到原始大小的矩阵。

在反卷积过程中，将每个特征数据与其对应的卷积核的转置进行卷积操作并将结果求和，再加上偏置c，激活函数不变。则输出y的计算公式如下：

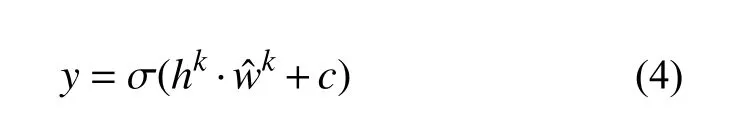
采用MSE(均方误差)函数作为损失函数，即目标值减去预测值的平方和再求均值，公式如下：

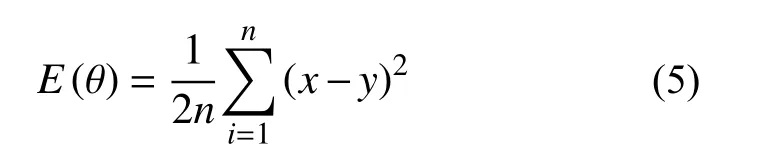
2 IPM-CAE 方法原理

为了从原始的振动响应信号中提取有效的损伤信息，提高计算效率，本文将内积矩阵与深度学习方法相结合，将内积矩阵作为CAE 网络的输入。将每个螺栓的S 种健康状态分为S 类，作为网络的输出，再使用CAE 网络来训练此分类问题。由于使用CAE 网络进行训练时需要大量带标签的数据，本文将每个传感器测得的加速度时域响应进行分组，从而构建标签数据库。将结构健康状态下每一个传感器的测试数据分为m组，每组的每一个响应测点均包含n个采样点，利用每组p个传感器的n个采样点，可以获得改组的内积矩阵，进而可一共获得m个内积矩阵，这就构成了结构在当前健康状态下的标签数据库。

在计算得到输入数据之后，需要将数据输入卷积自编码器中。本文所设计的卷积自编码器包括编码器、解码器、全连接层及softmax 分类层，其中编码器由两个卷积层和一个池化层组成，解码器由两个反卷积层和一个上采样层组成，它们将原始数据映射到隐藏特征空间，以提取数据特征。全连接层为一层，它将提取到的数据特征映射到样本标记空间。Softmax 分类层可以获得分类的概率[24]。基于卷积自动编码器进行螺栓松动状态监测的流程如图2 所示。

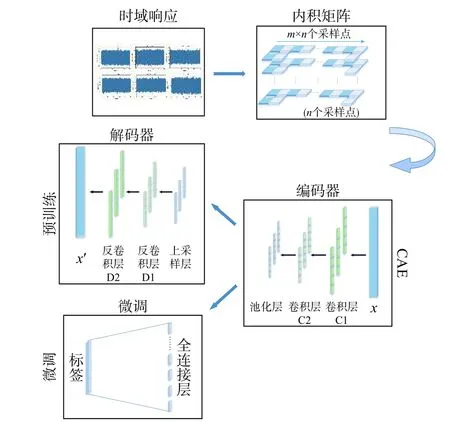
图2 螺栓松动状态监测过程图Fig. 2 Process diagram of bolt loosening state monitoring

具体监测流程如下：

步骤 1. 将振动响应数据集进行处理，计算其内积矩阵，以此作为神经网络的输入。

步骤 2. 设置合理的卷积自编码器网络结构。

步骤 3. 将处理好的内积矩阵分成训练集、测试集和验证集并输入CAE 网络。

步骤 4. 对网络进行无监督训练，以提取输入数据的特征。

步骤 5. 将内积矩阵数据作为网络的输入，将螺栓预紧扭矩编号作为标签，对网络进行有监督的训练。

步骤 6. 将测试集数据输入到CAE 网络中，测试网络的识别效果。

3 螺栓连接搭接板的螺栓松动状态识别研究

螺栓连接搭接板结构是航空领域常见的一种连接方式，本节将以此为研究对象来说明本文方法的可行性及有效性。

3.1 实验数据采集

本文采用的螺栓连接的搭接板由两块尺寸为150 mm×90 mm×2 mm 的 铝 板 组 成，并 由6 个M5 螺栓连接。搭接板两侧通过加持夹具固定在振动台上，以模拟两边固支边界。

根据内积矩阵的理论，构建内积矩阵时可采用任何环境激励作为激励源，考虑到航空结构在实际飞行过程中所受的环境激励通常可采用飞机振动环境试验谱进行模拟，因此本文采用某飞机振动环境试验谱作为环境激励，对搭接板进行激励。

实验中，在m+p VibControl 振动控制系统中设置振动环境试验谱，以驱动东菱ET-20 振动台及安装在其上的螺栓连接搭接板，并在搭接板上布置8 个PCB Piezoelectrics 333B30 加速度传感器(测量方向与振动方向相同，即垂直板面方向)，进而采用Dewesoft SIRIUS 数据采集仪采集各个测点的加速度响应信号。实验示意图如图3 所示，实验现场如图4 所示。针对每一种工况的实验，采样频率均为20 000 Hz，采样时长为10 min。

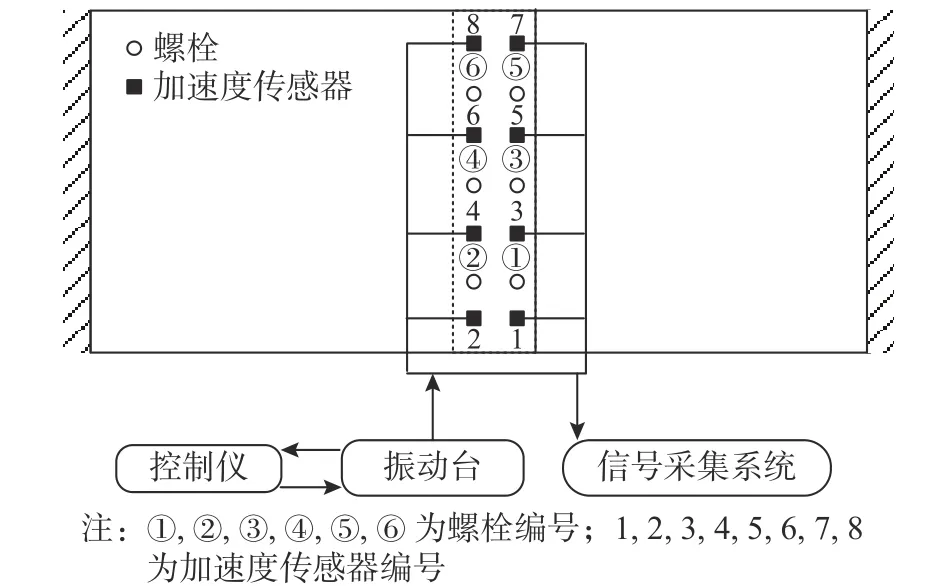
图3 实验示意图Fig. 3 Experimental schematic

图4 实验现场Fig. 4 Experimental setup

将6 个螺栓按顺序编号，分别为1 号～6 号，在每个螺栓旁边布置加速度传感器，共计8 个加速度传感器，来测量结构在随机激励下的加速度响应。去除采样开始的30 s 和结束的30 s 数据，最终选择9 分钟的数据进行数据库构建。对每个螺栓施加5 N·m 的预紧扭矩作为健康状态，当1 号～6 号螺栓的预紧扭矩均为5 N·m 时结构处于健康状态。试验时分别对每个螺栓进行松动，设置不同的预紧扭矩，间隔为0.5 N·m，其他螺栓保持5 N·m 不变。每个螺栓的预紧扭矩状态均为5 N·m、4.5 N·m、4 N·m、3.5 N·m、3 N·m、2.5 N·m、2 N·m、1.5 N·m、1 N·m、0.5 N·m、0 N·m，共11 种工况。按螺栓编号进行命名，如1-4.5，表示1 号螺栓预紧扭矩为4.5 N·m 的状态。以1 号螺栓为例，具体实验设置如表1 所示，健康状态和部分损伤状态的信号图如图5 所示。

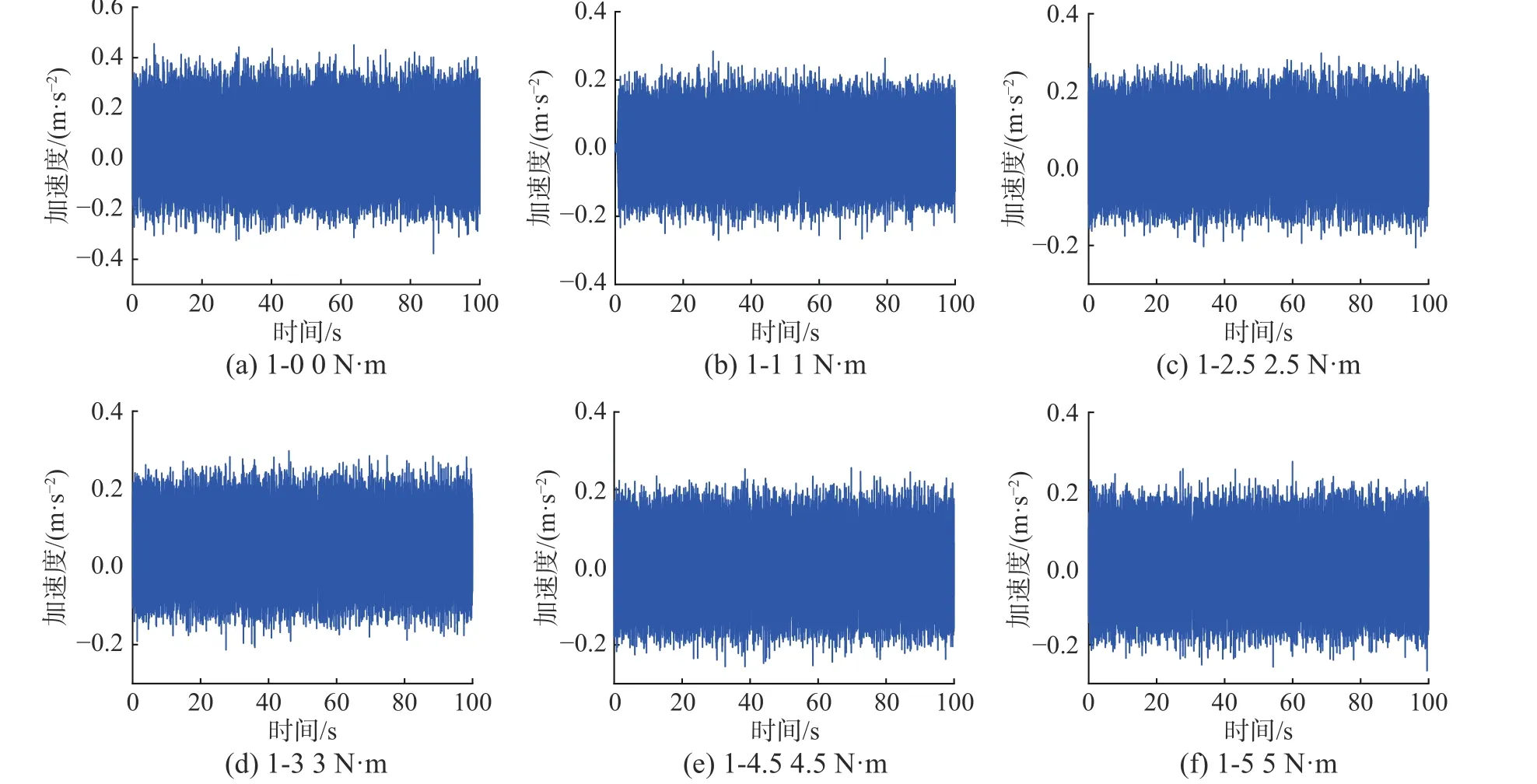
图5 1 号螺栓健康状态和部分损伤状态响应图Fig. 5 Responses of No. 1 bolt health status and partial damage status

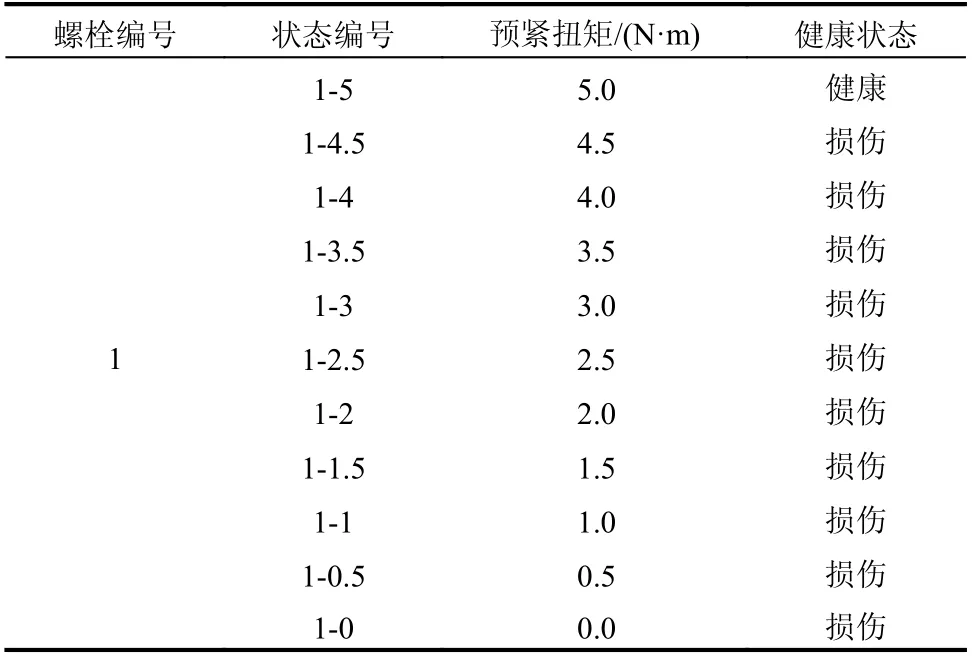
表1 实验编号设置Table 1 Experiment number setting

3.2 实验参数选择

在实验中，对每一个螺栓，共进行10 种损伤状态、1 种健康状态的测试，共获得11 组数据，每组数据均包含8 个测点的时域加速度响应。在计算内积矩阵时，增大n的值即增加采样点数，会增加损伤信息，从而可以提取更加显著的结构损伤特征。因此在损伤指标构建过程中，取n=8192，m=1024，即针对11 种结构健康状态，共计获 得11×1024=11 264 个 内 积 矩 阵。本 文 按 照8∶1∶1 的比例将数据划分为训练集，验证集和测试集。

对于IPM-CAE 网络模型，一些重要的参数会对网络的训练结果产生一定的影响，如卷积层的数量、卷积核的个数等。

本文研究了卷积层数和卷积核个数的影响。卷积核也称为滤波器[25]，分别使用 1 层、2 层和 3层 CAE 模型进行训练，具体模型参数如表2 所示。准确率定义为预测正确的结果占样本总数的百分比，是检测网络训练结果的重要指标。以1 号螺栓为例，训练185 个epoch 后，训练结果准确率如表2 最后一列所示。

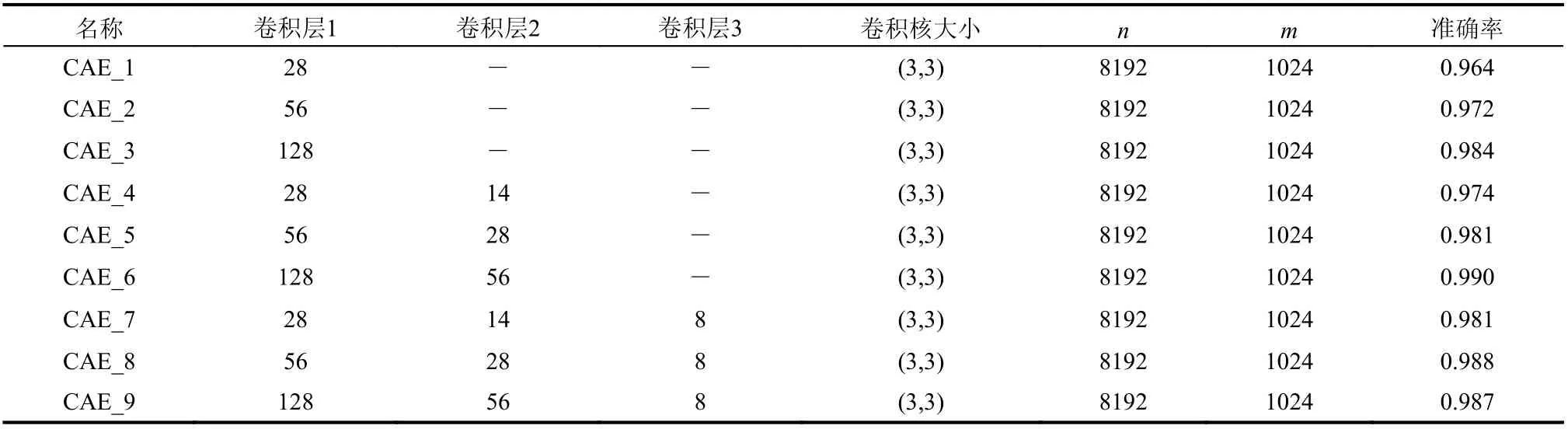
表2 CAE 模型结构对监测结果的影响Table 2 Effect of the structure of different CAE models on the detection results

从结果可以看出，9 种CAE 模型在进行185次的训练之后均取得了不错的监测效果。CAE_6的监测准确率最高，CAE_1 最低。因此适当增加卷积层数可以使网络学习到更复杂的特征表达，从而提高模型的准确率，更多的卷积核个数更加有利于提取信号的主要特征。尽管如此，太多的卷积层会导致模型面临梯度消失或梯度爆炸的风险，过多的卷积核会造成参数冗余，影响模型的训练结果。因此，本文选择CAE_6，即第一层卷积核个数为128、第二层为56 进行后续研究。

正则化系数用于减弱深层神经网络的过拟合效应，其候选集合为：L1 正则化和L2 正则化，参数值分别取0、0.001、0.01、0.1、0.5、0.9。学习率是指在优化算法中更新网络权重的幅度大小，用来控制权值更新的步长。学习率过大，可能会使损失函数直接越过全局最优点，训练容易产生振荡；学习率如果过小，损失函数的变化速度很慢，可能出现过拟合，并且很容易被困在局部最小值或者鞍点。学习率的候选范围为0.0001、 0.0005、 0.001、 0.005、 0.01、 0.05。batch_size 表示一次训练所取的样本数，其大小对模型的优化速度和程度都有影响，同时还会影响到计算机GPU 内存的使用情况，batch_size 的值越大，所使用的GPU 内存越大，然而过小的batch_size 会使梯度频繁变化，且不准确，从而导致网络很难收敛。batch_size 的候选范围为8、16、32、64、128、256、356、512、712。本文使用嵌套的五折交叉验证方法查找最佳参数。具体来说，产生最高分类精度的参数被选为后续研究的最佳参数。对比不同取值下模型训练的准确率，由结果可知，使用L2 正则化，参数值为0.01，学习率为0.001 时识别效果最好。

实验采用的最佳网络结构如表3 所示。在CAE 网络的编码阶段设置了两个卷积层和一个池化层。在两个卷积层中均使用‘ReLU’函数作为激活函数。为了平衡模型的复杂度和性能，防止过拟合，在卷积层中添加L2 正则化[26]，并将系数设置为0.01。自编码器的解码器和编码器对称，解码器中反卷积层也加入同样的激活函数和L2 正则化。优化器使用Adam[27]，并将学习率设置为0.001。

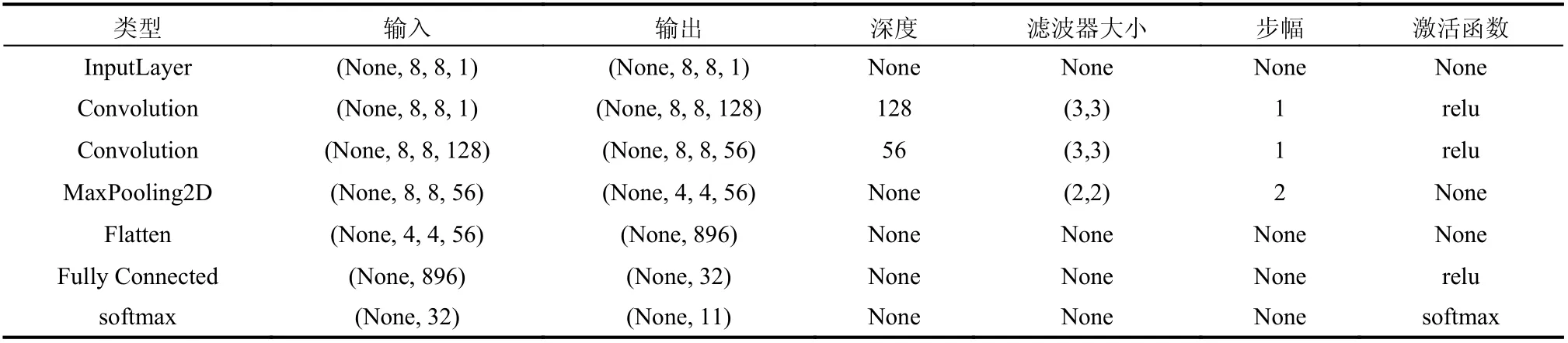
表3 最佳的CAE 网络结构Table 3 The best structure of CAE network

3.3 实验结果分析

用1 号～6 号螺栓在不同预紧扭矩下实验测得的加速度响应数据求解内积矩阵，并将求得的数据输入设计好的CAE 网络中，对螺栓的预紧扭矩进行监测。实验中每个螺栓共11 种健康状态，因此预紧扭矩的监测为多分类问题，在神经网络中将11 种工况分为11 类。6 个螺栓的松动状态监测结果如图6 所示，测试集准确率如表4 所示。

表4 6 个螺栓测试集准确率Table 4 Accuracy of 6 bolts test sets

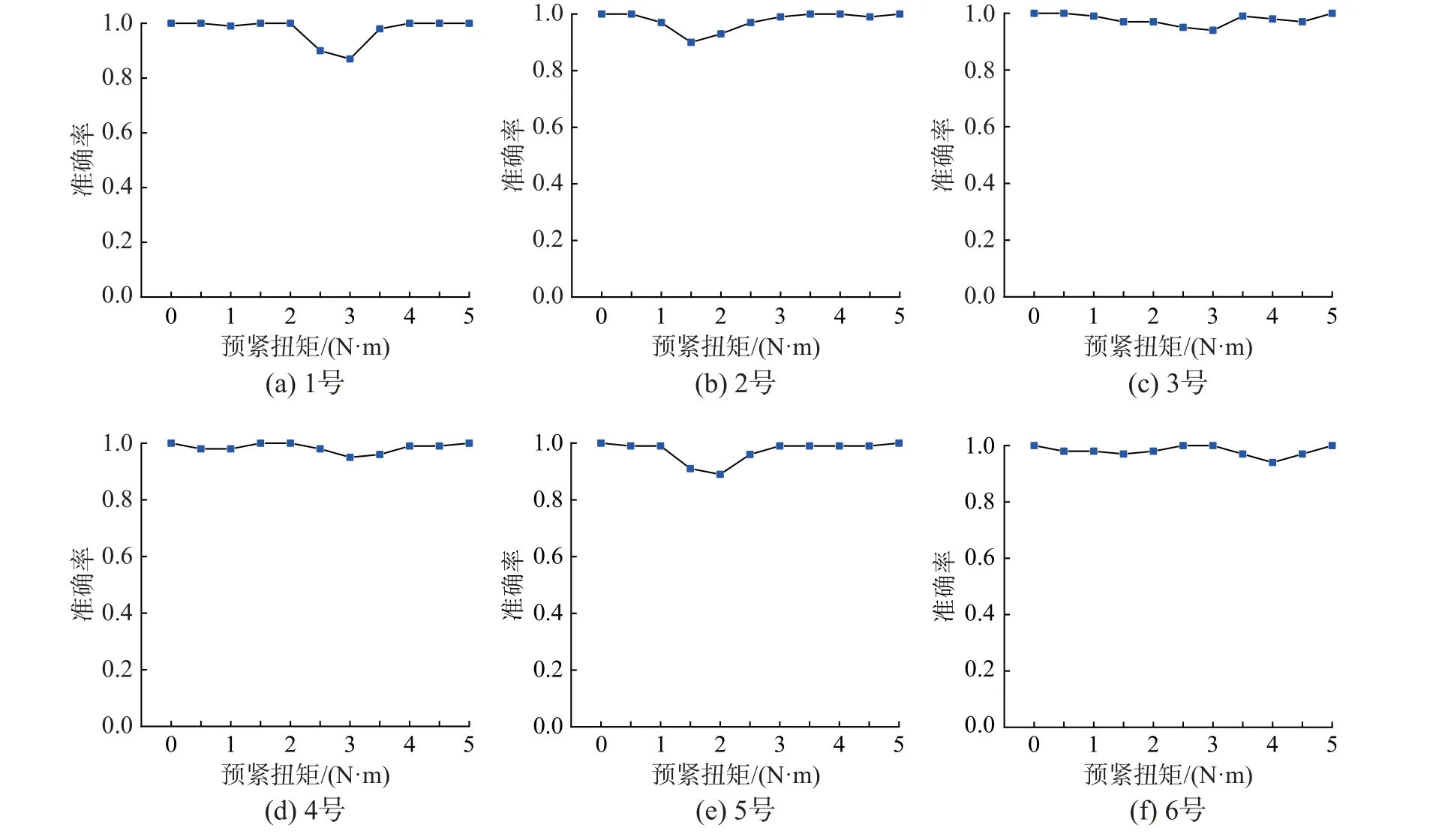
图6 6 个螺栓的松动状态监测结果Fig. 6 Monitoring results of the loose states of 6 bolts

由结果可知，对1 号～6 号螺栓的预紧扭矩监测均取得了较好的效果。其中，5 号螺栓测试集准确率达到了97%，1 号螺栓为99%，其他螺栓均为98%。从图7 可以看出，对1 号来说，当预紧扭矩为2.5 N·m 和3 N·m 时监测效果最差，此时二者测试集的准确率分别为90%和88%，其他预紧扭矩的准确率均在98%以上。对5 号螺栓，当预紧扭矩为1.5 N·m 和2 N·m 时监测效果相对较差，此时二者测试集的准确率分别为90%和88%，其他预紧扭矩的监测准确率均在95%以上。对2 号螺栓，当预紧扭矩为2 N·m 时监测效果相对较差，测试集准确率为93%，其他预紧扭矩的监测准确率均在95%以上。对3 号、4 号、6 号螺栓，监测其预紧扭矩的准确率均在95%以上。

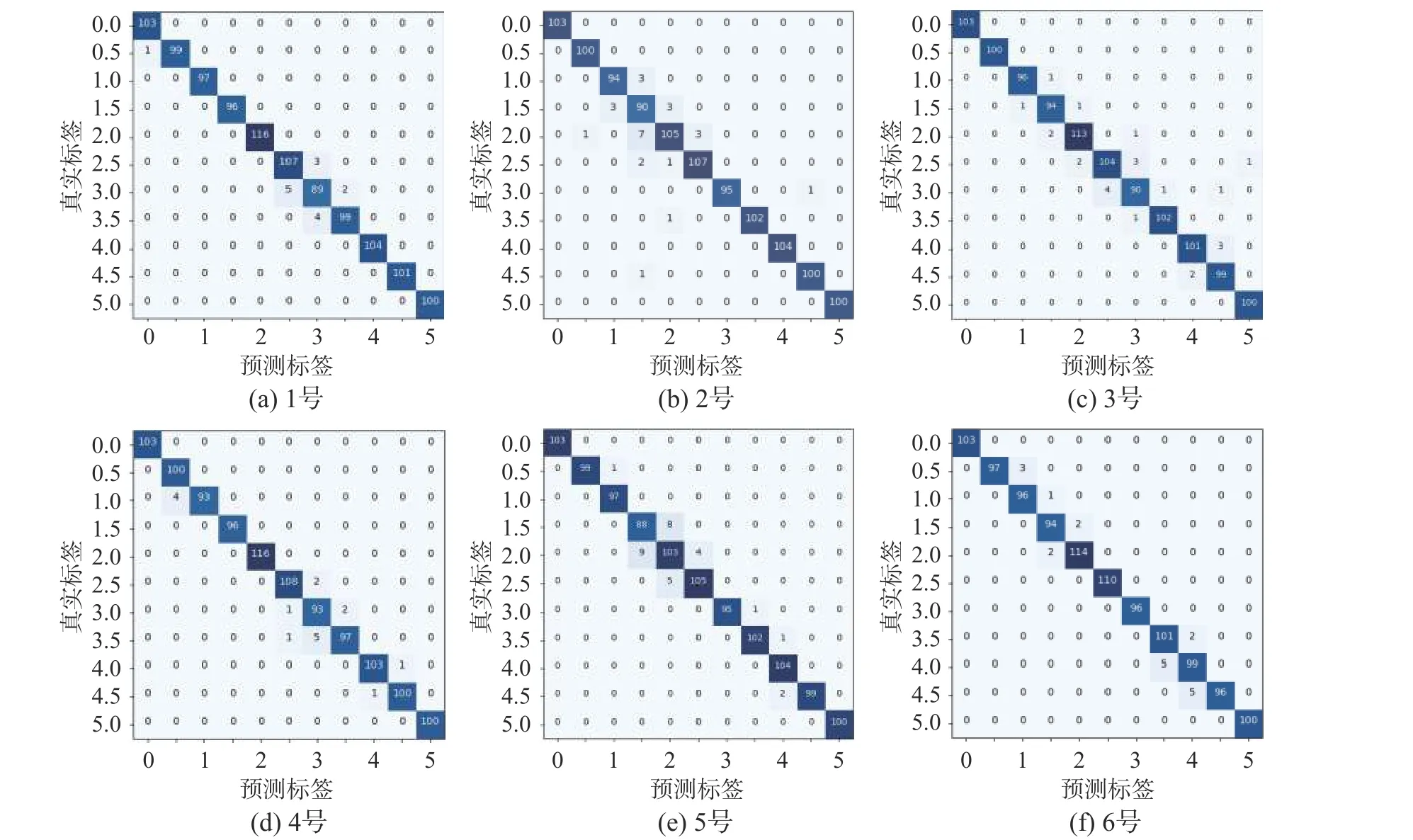
图7 6 个螺栓的预紧扭矩混淆矩阵Fig. 7 Confusion matrix of 6 bolts pre-tightening torques

4 不同方法测试结果的对比

为了验证本文所提CAE 神经网络的有效性，将CAE 网络和SAE、CNN、CapsNet 进行对比。其中，CNN 网络包含两个卷积层和一个池化层。第一个卷积层中卷积核的个数为128，大小为3×3，第二个卷积层中卷积核的个数为56，大小为3×3，在卷积层中加入系数为0.01 的L2 正则化，设置学习率为0.001。SAE 网络包括两个隐藏层，隐藏层大小分别为128 和56，隐藏层中同样加入系数为0.01 的L2 正则化，将网络优化器的学习率设置为0.001。对CapsNet，本文使用Hinton论文中提出的模型进行计算。上述模型的batch_size均为128，在互相关矩阵的计算中n=8192，m=1024，训练次数均为185 次。网络的对比结果如表5 所示，训练曲线如图8 所示。

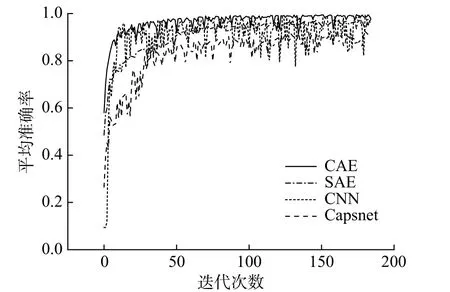
图8 不同网络的训练曲线Fig. 8 Training curves of different networks

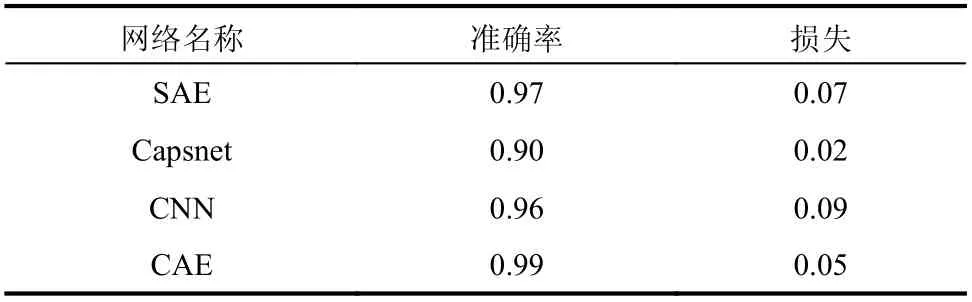
表5 不同网络的对比结果Table 5 Comparison results of different networks

由结果可以看出，在四种网络中，本文所提CAE 网络的效果最好，测试集准确率达到了0.99，损失值为0.05，训练曲线具有较高的收敛效率。SAE 网络次之，测试集准确率为0.97，与CAE 相比，它收敛速度较慢，迭代效率不高。对CNN 网络，测试集准确率为0.96，其验证集曲线波动较大，这会导致监测结果不稳定。CapsNet 的训练曲线波动也较大，且测试集准确率不高，仅为0.90，但损失值较小，为0.02。由以上结果可知，与其他网络相比，本文所提CAE 网络具有较好的监测螺栓连接搭接板中螺栓的松动状态的能力。

5 模型性能优化

在准确率达到预计要求后，本文开展了进一步优化，寻找在使用尽可能少的加速度传感器的情况下保持较高的监测准确率的方法。在上文中使用了 8 个加速度传感器数据进行监测，本节改变加速度传感器的数量，分别测试传感器数量为6、4、2 时网络结构的识别情况。其中使用 6 个传感器进行监测，即使用1 号、3 号、4 号、5 号、6 号、8 号传感器；4 个传感器，即使用1 号、4 号、5 号、8 号传感器；2 个传感器，即使用2 号、7 号传感器。

对CAE 网络，将测点数量设置为6，准确率变为95.5%；将测点数量设置为4，准确率为91.0%；将测点数量设置为2，准确率为53.1%。说明减少传感器数量会降低螺栓松动状态监测的准确率。对模型进行优化，一般认为，在不发生过拟合情况时，网络收敛性能的减弱与数据集信息量不足有很大的关系。因此，本文增加网络中输入数据的数据量，并判断其对网络监测性能的影响。

本文原截取数据的方法是每隔8192 个采样点截取一次数据求解其内积矩阵，作为输入数据。现增大数据量，即增加计算内积矩阵时截取数据的采样点数，这种截取方法使输入的数据中包含了更大的信息量。为了进一步验证输入数据量的大小以及测点数量对网络性能的影响，将截取采样点的长度分别设置为8192、9216、10 240、11 264，测点数量设置为6、4、2，对不同输入下的模型进行训练，结果如表6 所示。由结果可知，减少传感器测点的数量会使网络性能下降。此时通过更改网络中输入的数据量，采用间隔更长的数据划分方式可以有效提高网络性能。

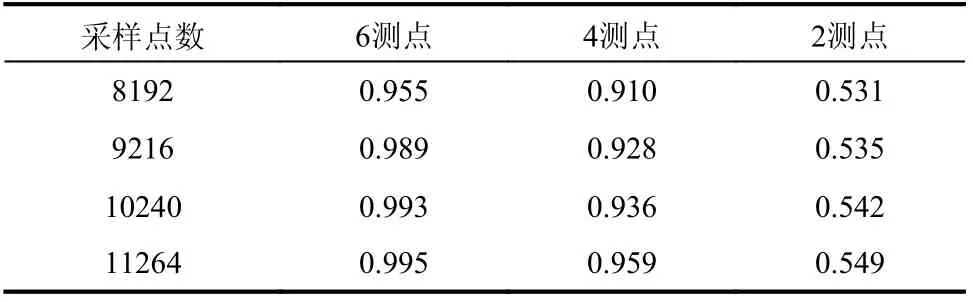
表6 不同采样点数和测点数量下的准确率对比Table 6 Comparison of accuracy rates under different sample points and measurement points

6 结论

本文利用环境激励下的结构振动响应及深度学习技术，提出基于卷积自编码器的螺栓松动状态监测方法。首先，将结构在环境激励下的时域振动响应数据作为原始信号，并利用时域响应的内积向量法，获得描述结构健康状态的损伤特征指标。其次，以获得的损伤特征指标为输入构建了卷积自编码器。最后，以螺栓连接的搭接板为研究对象，进行了螺栓松动状态监测的实验研究，结果表明：

(1) 本文方法在时域响应的内积矩阵计算过程中会自动剔除相关测量噪声的影响[28]，从而获得更好的结构损伤特征，可作为输入数据用于深度神经网络的训练。

(2) 使用卷积层和池化层代替自编码器的全连接层，可以实现对输入信号的线性变换，更好的保留输入数据的特征信息，减少重构误差，提高网络的特征提取能力。

(3) 与基于 IPM 的卷积神经网络 、堆栈自动编码器和胶囊网络(即 IPM-CNN 、IPM-SAE 和IPM- CapsNet)相比，本文提出的IPM-CAE 方法显示出更好的网络训练收敛速度和识别精度。

(4) 在总数据量不变的前提下，减少传感器测点的数量并增加计算内积矩阵时截取数据的采样点数，本文方法仍可以保持较高的监测准确率。

(5) 本文方法与大部分基于神经网络的方法类似，其不足之处是需要完备的训练集，下一步将结合基于深度迁移学习的相关理论方法，以提升本文方法在训练集不完备情况下的监测精度。