带球冠形脱空缺陷椭圆钢管混凝土短柱轴压性能及计算方法研究

沈奇罕，王静峰，李景哲

(1. 合肥工业大学土木与水利工程学院，合肥 230009；2. 先进钢结构技术与产业化安徽省协同创新中心，合肥 230009；3. 土木工程结构与材料安徽省重点实验室，合肥工业大学，合肥 230009)

钢管混凝土由于在强度、塑性、韧性和抗震性能等方面的显著优势，近年来在超高层建筑、大型桥梁工程、重载交通和海洋开发等领域被广泛应用[1−3]。然而，据相关部门对我国部分钢管混凝土桥梁拱肋及墩柱的检测发现，其中大量结构存在核心混凝土的脱空问题，追溯其原因主要与混凝土材料质量不合格、灌注混凝土施工方式不规范、内外养护温差大和混凝土材料收缩等因素有关[4− 5]。

根据核心混凝土脱空形状的不同，核心混凝土脱空主要分为“球冠形脱空”和“环向脱空”。其中，球冠形脱空常见于诸如钢管混凝土桁架、桥拱等水平跨越构件，主要是由于钢管混凝土构件浇筑时截面顶部产生气腔、泌水等现象，致使混凝土与钢管的部分界面发生脱离。众所周知，钢管混凝土构件的力学性能优势主要在于钢管与混凝土之间的组合互补与协同工作，即钢管能为核心混凝土提供环向约束，提高其强度与延性；混凝土则为外围钢管提供侧向支撑、抑制或延缓其局部屈曲。但脱空间隙的出现会导致混凝土与钢管之间的界面发生局部脱离、削弱甚至消除外部钢管与内部混凝土间的支撑与约束行为，降低钢管混凝土构件相对应的力学性能(如承载力、刚度和延性等)[4]。忽略核心混凝土脱空缺陷的影响可能造成实际工程存在一定的安全隐患，严重时可能导致人员伤亡和经济损失。

为明确钢管混凝土内部脱空对其受力性能的影响，部分学者对带脱空缺陷方形、圆形钢管混凝土构件进行了研究[4−5]。如叶跃忠等[6]、李永进等[7]、叶勇等[8]、HAN 等[9]和云迪等[10]分别对带脱空缺陷钢管混凝土构件的轴压、偏压和受剪性能进行了研究，明确了脱空率、含钢率和材料强度等重要参数对其受力性能的影响，揭示了脱空缺陷对钢管混凝土构件承载力、刚度和稳定性的作用机制。廖飞宇等[4− 5]则对带脱空缺陷圆钢管混凝土构件在单一静力(压、弯、扭、剪)和复杂荷载下的受力性能进行了系统的试验研究、数值模拟和力学分析工作。至此，带脱空缺陷圆形/方形钢管混凝土构件的受力性能与设计方法初步形成系统。

然而，随着现代社会对建筑外观美学和结构效率要求的提高，普通钢管混凝土已逐步无法满足需求。其中，椭圆钢管混凝土由于截面形态分布灵活、建筑美学效果好和流阻系数小，近年来被广泛的应用于机场航站楼、大型桥梁和大跨空间等重要公共工程中[11]。尽管目前国内外学者[11−18]及本课题组[19− 20]对椭圆钢管混凝土构件的单一静力、复杂受力和抗震性能已开展了一系列的研究，但鉴于混凝土脱空引发工程结构安全问题的严重性和其成型原因的客观性，有必要进一步研究混凝土脱空对椭圆钢管混凝土构件受力性能的影响。

本文通过设计并测试11 根带球冠形脱空椭圆钢管混凝土短柱试件，开展轴压性能试验，分析破坏形态、轴压承载力、初始刚度和延性等性能在球冠形混凝土脱空影响下的变化规律，明确其截面应变分布和核心混凝土强度特征，最终提出考虑椭圆截面特征和球冠形脱空影响的椭圆钢管混凝土短柱轴压承载力计算公式。

1 试验概况

1.1 试件设计

本试验共设计了包括2 根椭圆空钢管短柱、2 根无脱空椭圆钢管混凝土短柱和7 根带球冠脱空椭圆钢管混凝土短柱。椭圆钢管截面尺寸2a×2b×t=280 mm×140 mm×6 mm(其中2a为椭圆长轴外径，2b为椭圆短轴外径，t为钢管厚度)，柱高设为500 mm(柱高径比L/2b约为3.5)。其中，球冠形脱空的成形方式与文献[21 − 22]相同。试件信息及脱空示意图如图1 和表1 所示。

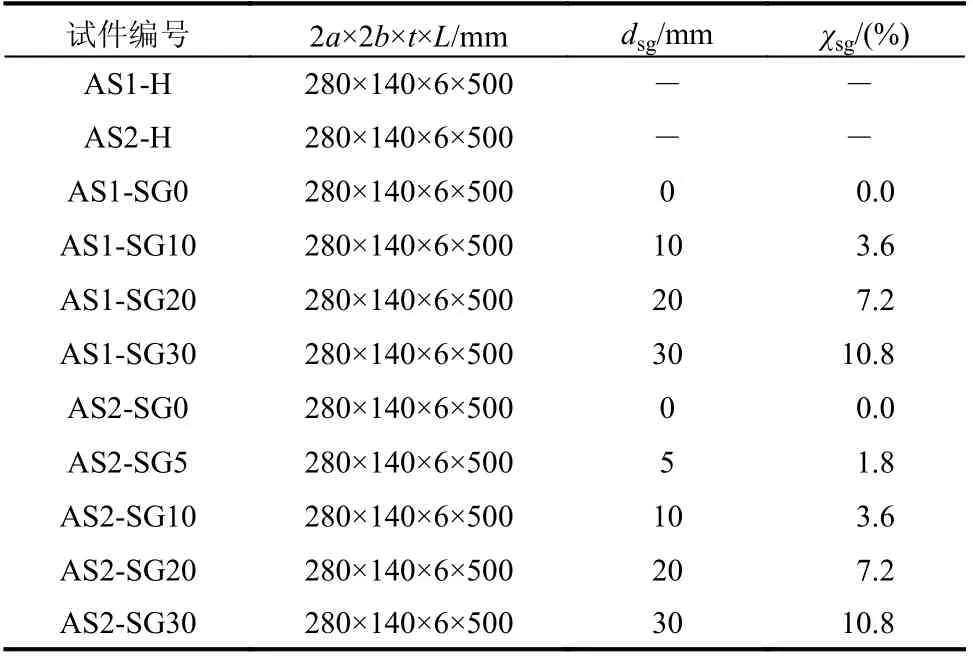
表1 试件几何信息表Table 1 The geometric information of test specimens

图1 带球冠形脱空试件示意图Fig. 1 The design diagram of test specimen with spherical-cap gaps

1.2 材料材性

试件中S1 和S2 分别代表钢材强度等级为Q235 和Q345 的圆形钢管经椭圆模具冷压成形的椭圆钢管，与文献[19, 23]中试件为同批次椭圆钢管。由于椭圆管各点的曲率不同，因此依据现行规范GB/T 2975−2018[24]，分别对不同位置进行材性试验。椭圆钢管的弹性模量(Es)、屈服强度(fy)、极限强度(fu)和伸长率(δ)等关键指标的测试平均值和取样位置及结果如图2 和表2 所示。

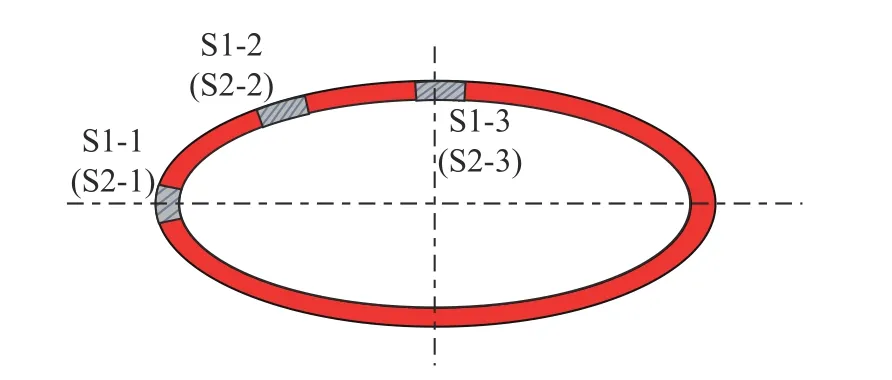
图2 拉伸试件取材位置Fig. 2 The position of the tensile coupons

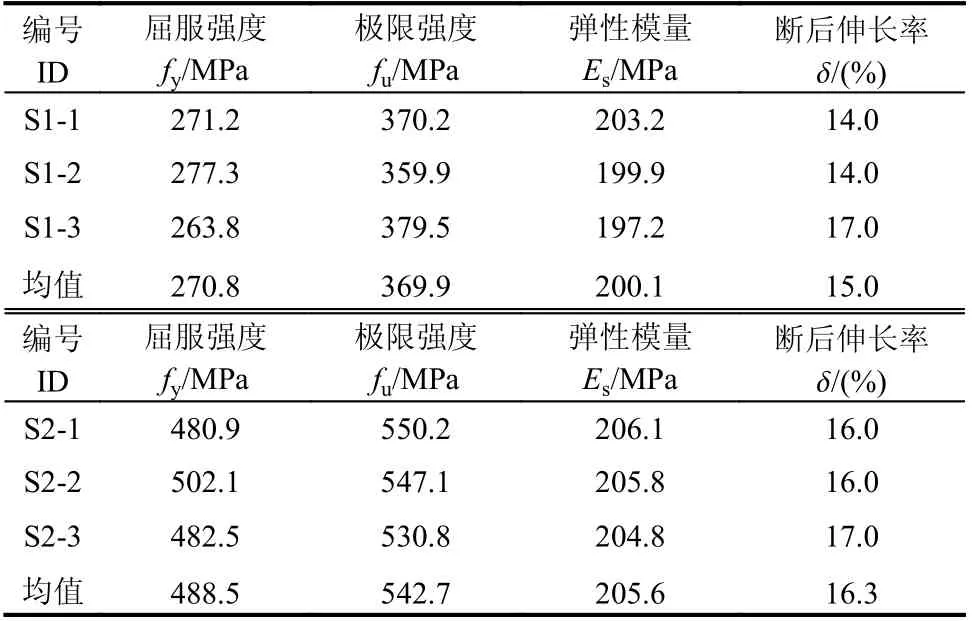
表2 钢管材性试验结果Table 2 The results of steel coupon test

试件均采用强度等级为C60 的自密实混凝土，依据规范(GB/T 50081−2019)[25]，测得的抗压强度标准值(fcu,k)和弹性模量(Ec)如表3 所列。

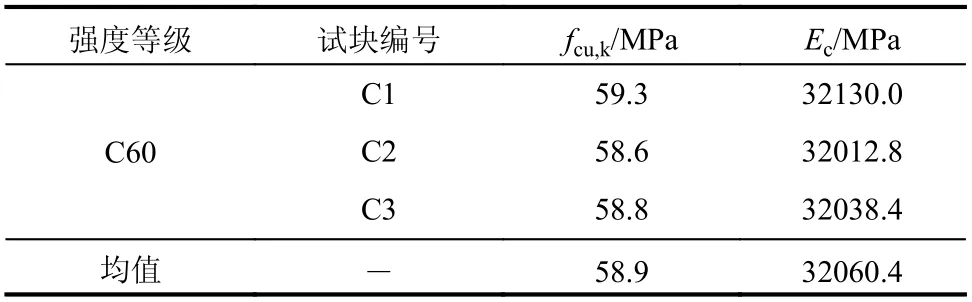
表3 混凝土材性测试结果Table 3 The test results of concrete material property

1.3 加载装置及量测内容

试验在5000 kN 多功能液压伺服试验机上进行，采用力-位移混合加载，见文献[26 − 27]。加载全过程实时采集力和位移响应，详细加载及量测示意图如图3 所示。

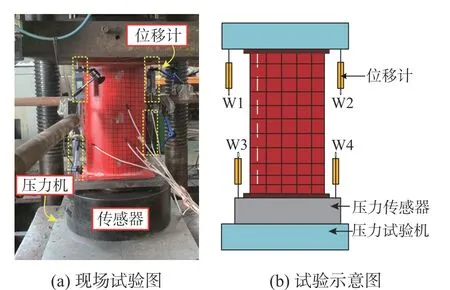
图3 试验加载及量测装置Fig. 3 Test loading and measuring devices

2 试验现象记录

2.1 破坏形态

试验表明：椭圆空钢管轴压短柱的破坏形态主要表现为钢管的局部凹陷；相比而言，无脱空椭圆钢管混凝土轴压短柱的钢管由于内部核心混凝土提供的支撑作用，钢管内凹行为被局部向外鼓曲取代，同时核心混凝土在压力作用下发生开裂与斜剪面破坏。值得注意的是，核心混凝土的斜剪面破坏主要沿着弱轴方向出现，这是由于椭圆形钢管曲率较小的部分对核心混凝土的约束较弱。因而在轴压力作用下，核心混凝土沿椭圆截面弱轴方向出现斜剪面破坏，表现出典型的脆性特征，如图4(a)所示。

当核心混凝土出现球冠形脱空时，椭圆钢管混凝土轴压短柱在球冠形混凝土脱空影响下的破坏模式除上述形态外，还可能出现脱空侧混凝土破碎、钢管局部凹陷和试件倾向于混凝土脱空侧整体弯曲的现象，如图4(b)所示。通过对比表明：当脱空率较小时，带球冠形脱空椭圆钢管混凝土轴压短柱的破坏模式与无脱空试件类似，但脱空界面处混凝土因缺乏钢管约束而出现大范围的破碎；随着脱空率的进一步增大，脱空区域钢管开始出现内凹屈曲的现象，同时由于荷载中心线要试件整体截面的中轴线位置的偏差，带球冠形脱空椭圆钢管混凝土轴压短柱进而出现了偏向于脱空侧的整体弯曲破坏。

图4 试件破坏形态Fig. 4 Failure patterns of test specimens

2.2 荷载(N)-位移(Δ)曲线

通过试验记录试验曲线(图5)，有如下发现：

1)椭圆空钢管试件、无脱空椭圆钢管混凝土试件和带球冠形脱空椭圆钢管混凝土试件的轴压荷载-位移曲线具有一定的相似性，均存在明显的下降段，但曲线下降段幅度与钢材强度和脱空率有关。

2)钢材强度的提高使带球冠形脱空椭圆钢管混凝土轴压试件的荷载-位移曲线下降段逐渐平缓。这可能是因为在相同条件下，钢管对核心混凝土的约束作用会随着钢管强度提高而有所增强，进而导致试件的延性和变形能力显著提升，如图5(a)所示。

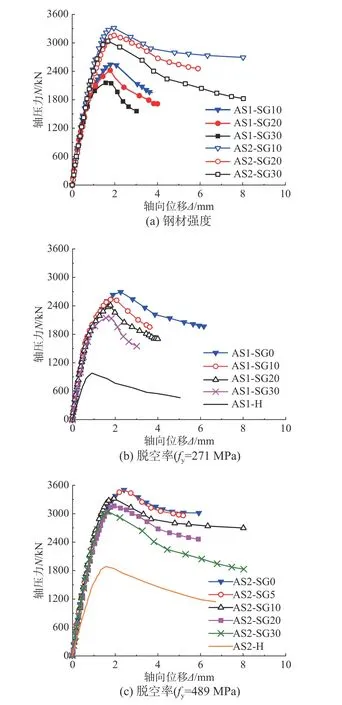
图5 荷载-位移曲线Fig. 5 The force - displacement curves

3)球冠形脱空率的增大导致椭圆钢管混凝土轴压试件的截面面积和刚度有所减小，试件的轴压强度和初始刚度有所减小；同时，脱空率增大扩展了无约束脱空界面，使核心混凝土的约束效果减弱，脆性更加明显。因此，试件荷载-位移曲线的下降段斜率有所增大，如图5(b)～图5(c)所示。

3 试验结果分析

3.1 峰值承载力(Nut)与初始刚度(Ki)

根据荷载位移曲线，确定试件的峰值承载力与初始刚度，详细结果表4 所示。具体研究结论如下：

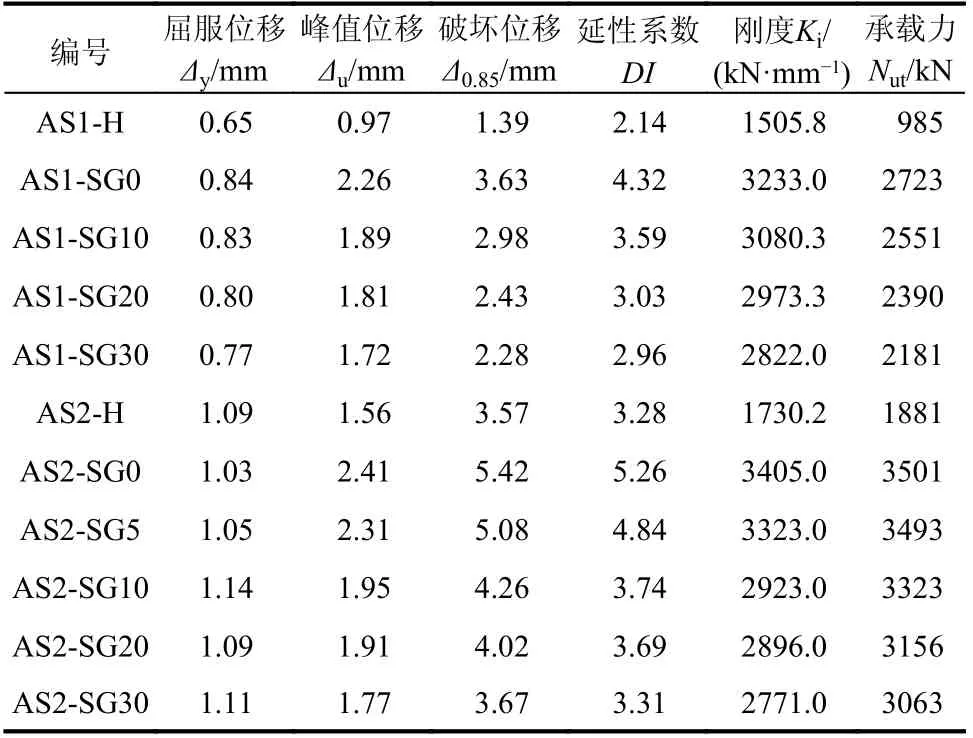
表4 试验结果Table 4 The test results

1)钢材屈服强度为489 MPa 的试件AS2-SG0、AS2-SG10、AS2-SG20 和AS2-SG30 的 峰 值 承 载力比钢材屈服强度为271 MPa 的试件AS1-SG0、AS1-SG10、AS1-SG20 和AS1-SG30 依 次 提 升 了28.6%、30.3%、32.1%和40.4%，但试件之间的初始刚度差接近于零。表明带球冠形椭圆钢管混凝土短柱的轴压承载力随着钢材强度的提高而增大。

2)当钢管屈服强度为271 MPa 时，沿截面长轴方向出现球冠形脱空间隙为10 mm、20 mm 和30 mm 的椭圆钢管混凝土短柱(试件AS1-SG10、AS1-SG20 和AS1-SG30)的轴压承载力比无脱空缺陷椭圆钢管混凝土短柱(试件AS1-SG0)依次降低了6.3%、12.4%和19.9%，初始刚度依次降低了4.7%、8.1%和12.7%；同样，当钢管屈服强度为489 MPa 时，沿截面长轴方向出现球冠形脱空间隙为5 mm、10 mm、20 和30 mm 的椭圆钢管混凝土短柱(试件AS2-SG5、AS2-SG10、AS2-SG20 和AS2-SG30)在轴压作用下的初始刚度比无脱空缺陷椭圆钢管混凝土短柱(试件AS2-SG0)依次降低了约2.4%、14.2%、14.9%和18.6%，承载力对应下降了0.3%、5.1%、9.8%和12.5%。研究表明：当球冠形脱空率不大于1.8%时，脱空缺陷对椭圆钢管混凝土短柱的轴压承载力和初始刚度影响较小；当脱空率大于3.6%时，椭圆钢管混凝土短柱的轴压承载力和初始刚度会随着球冠形脱空的增大显著降低。

3.2 荷载(N)-应变(ε)响应

基于应变片采集数据，图6 给了典型带球冠形脱空椭圆钢管混凝土轴压短柱在柱高中部钢管的关键位置的荷载-应变曲线，其中纵向压应变为负值，环向拉应变为正值，详细结果如下：

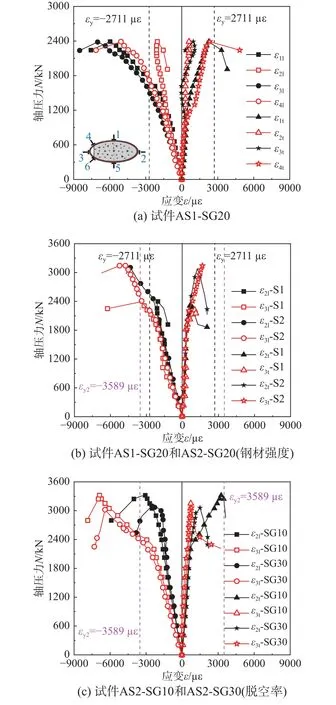
图6 荷载-应变曲线Fig. 6 The load- strain curves

1)由于脱空缺陷的出现，导致轴压下椭圆钢管的纵向和环向应变表现出明显的不对称性。脱空侧(3 号)钢管的纵向应变明显大于其他位置的，并率先屈服；在脱空侧对立面(2 号)的应变在轴向变形增大的过程中也逐步增大，然而由于脱空缺陷的存在，促使椭圆钢管混凝土短柱在受力后期产生倾向于脱空侧的整体弯曲。因此，脱空侧对立面由于“弯曲”效果，原先的纵向压应变和环向拉应变反而随着进一步加载而有所减小。

2)基于环向应变分析可知，带球冠形脱空缺陷椭圆钢管混凝土轴压短柱的环向应变在峰值荷载前均未屈服，与其他类型钢管混凝土轴压柱的规律一致。测点1 号和4 号处的环向应变明显高于2 号和3 号处。这可能是由于1 号和4 号处钢管与混凝土之间的接触作用良好，环向应变充分发展；3 号位置钢管与混凝土无接触应力，环向应变较小。而2 号位置处虽然有良好的接触条件，但是由于脱空引发的“弯曲”效应，其环向应变发展较慢，相对较小。

3)通过对比不同钢管强度和脱空率的带球冠形脱空缺陷椭圆钢管混凝土轴压短柱截面脱空侧和其对立面的应变可知，钢材强度的提高对试件的应变发展规律影响较小，而随着球冠形脱空率的增大，脱空侧的纵向压应变发展更快。相反，脱空侧对立面的纵向应变由于“弯曲”效应，其压应变较小，且发展相对缓慢。

3.3 延性系数

本节引入延性系数µ，以获悉各试件的延性性能，表达如下：

式中：Δy为试件屈服荷载对应的纵向位移；Δ0.85定义见参考文献[14]，计算结果如表4 所示。研究结果表明：

1)在脱空率一致的条件下，带球冠形脱空椭圆钢管混凝土的延性系数随着钢材强度提高而增大。这是由于钢材强度的提升会显著提高核心混凝土受到的约束作用，从而表现出较好的延性性能。

2)在钢材强度相同的条件下，球冠形脱空率的增大会逐步降低椭圆钢管混凝土轴压短柱的延性系数。原因在于，随着脱空率的增大，脱空界面面积显著增大，无约束和部分约束状态下的核心混凝土面积持续增大，带球冠形椭圆钢管混凝土轴压短柱的延性性能逐渐减小。

3.4 脱空特征系数

为进一步明晰球冠形脱空对核心混凝土所受约束作用的影响，参考文献[21, 23]，引入脱空特征系数GFI，具体表达式如下：

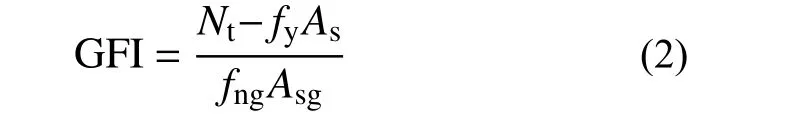
式中，相关符号及取值参考文献[23]。

由图7 可知，对于带球冠形脱空缺陷的椭圆钢管混凝土短柱，GFI 随脱空率的增加而减小。对于钢管屈服强度为489 MPa 的试件，当脱空率分别为3.6%、7.2%和10.8%(试件AS2-SG10、AS2-SG20 和AS2-SG30)时，GFI 分别为0.90、0.82 和0.78；同样地，对于钢管屈服强度为271 MPa 的试件，当球冠形脱空率分别为3.6%、7.2%和10.8%(试件AS1-SG10、AS1-SG20 和AS1-SG30)时，GFI分别为0.91、0.83 和0.72。结果表明：带球冠形脱空缺陷椭圆钢管混凝土轴压短柱的脱空特征系数值均小于1。表明球冠形脱空对椭圆钢管混凝土轴压承载力的影响不仅仅是单纯意义上核心混凝土面积的减小球冠形脱空的增大，核心混凝土所受的约束作用也会持续减弱。

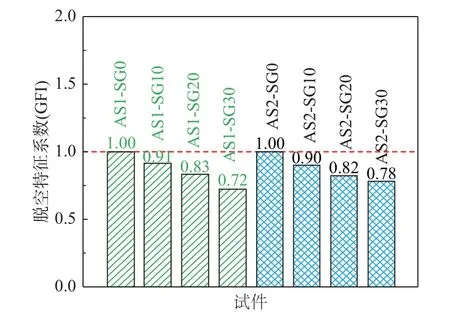
图7 试件脱空特征系数Fig. 7 The GFI of test specimens

虽然，目前国内外在检测钢管混凝土脱空缺陷方面已形成了相当成熟的理论及方法[28]。但尚未见带脱空椭圆钢管混凝土短柱的轴压承载力评估与预测方法方面的相关报道。文章基于椭圆截面特征和带球冠形脱空核心混凝土约束分区模型，提出了带球冠形脱空椭圆钢管混凝土短柱的轴压承载力计算公式，具体如下：

4 承载力计算方法

式中：Ns和Nc分别为椭圆钢管和核心混凝土截面所能承担的荷载；Nfc、Npc和Nc0分别为核心混凝土强约束区、弱约束区和无约束区的截面承载力；Afc和fcc为强约束区混凝土截面积和抗压强度；Apc和fpc为弱约束区混凝土截面积和抗压强度；Ac0和fc0为无约束区混凝土截面积和抗压强度。

以椭圆钢管混凝土主轴方向脱空为例(见图8(a))，令椭圆内径主半轴为ai，次半轴为bi；令脱空界面与椭圆曲线在第一象限交点为(m,n)，经过原点和(m,n)点的直线为y=k1x。假定核心混凝土无约束区域是由抛物线l1与脱空界面围成，令抛物线l1为y=asgx2+c与直线y=k1x相切于(m,n)点，对抛物线方程在(m,n)点求导可得：

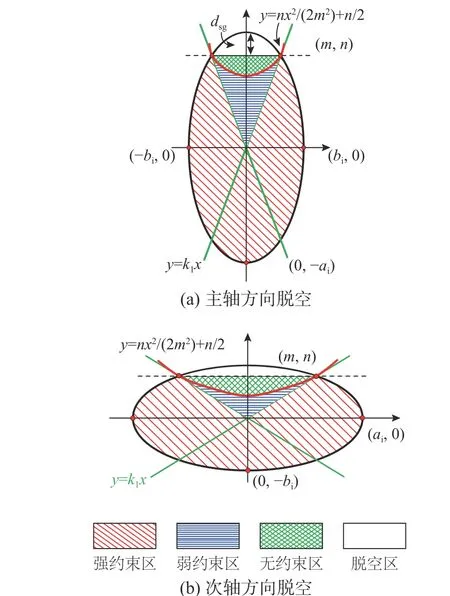
图8 带球冠形脱空椭圆核心混凝土约束分区模型Fig. 8 The confining status model of the elliptical core concrete with spherical-cap gap

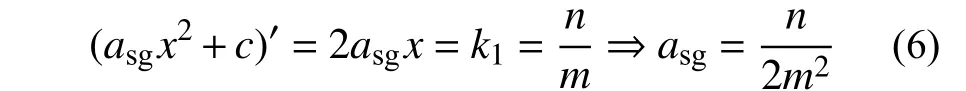
当x=m时，y=n，则有，c=n/2，即抛物线l1方程为：

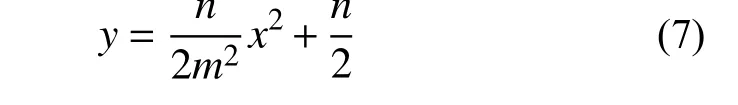
此时，对抛物线l1在x∈(−m,m)区间内进行积分可计算无约束区混凝土面积(Ac0)：

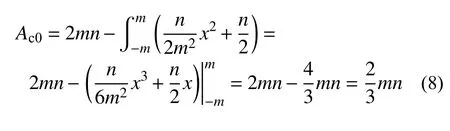
同理，对于弱轴方向的脱空如图8(b)所示，则弱约束区域面积(Apc)则为(−m,n)、(m,n)和原点连成的三角形区域与无约束区域的面积差，具体表达为：

同理，基于上述计算，亦可明确短轴球冠形脱空时，各类区域的的面积。

对于各区域的混凝土抗压强度，可基于混凝土约束理论进行推导。根据相关研究[15− 16, 29]表明：椭圆钢管核心混凝土约束力分布表现为长轴端点最大，并自长轴端点向短轴端点依次递减的规律。假设短轴半对称体的平均约束强度为fr1，长轴半对称体的平均约束强度为fr2，则核心混凝土所受的平均约束强度必然介于两者之间。

基于上述假定，对椭圆钢管和核心混凝土取半对称体(如图9)，则在长、短半轴方向的约束应力和钢管环向力有静力平衡方程：

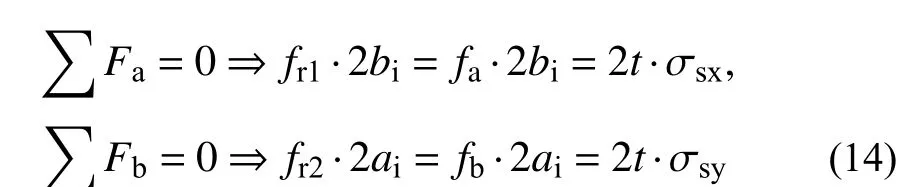
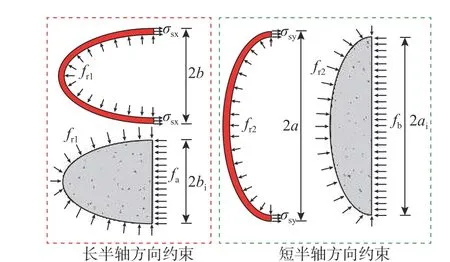
图9 椭圆核心混凝土侧向约束假定Fig. 9 The assumption of the lateral confining force of elliptical core concrete

有别于钢管约束混凝土，钢管混凝土轴压短柱中钢管和混凝土共同承担纵向力，钢管在纵向率先达到屈服应力，而环向应力相对发展略慢，详细结果如本文3.2 节所述。在钢管纵向应力达屈服状态的情况下，基于钢材泊松比0.3，假定环向应力为0.3fy。则可解得：

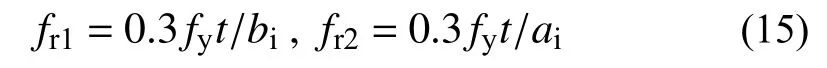
由式(15)可知，椭圆核心混凝土所受的约束力随着椭圆截面各处曲率的变化而有所不同。为简化计算，本文假定椭圆核心混凝土的平均约束应力为：

对于弱约束区的混凝土，其抗压强度应介于强约束和无约束混凝土之间。为简化计算，假定弱约束区混凝土抗压强度为：

基于上述约束分区思路和相关假定，表5 将公式计算结果与本文及文献[4]中带球冠形脱空钢管混凝土短柱的轴压承载力试验值进行对比分析。对比结果表明：本文提出公式的计算结果与试验结果吻合良好，比值(Nc/Nut)均值为1.00，方差为0.003。

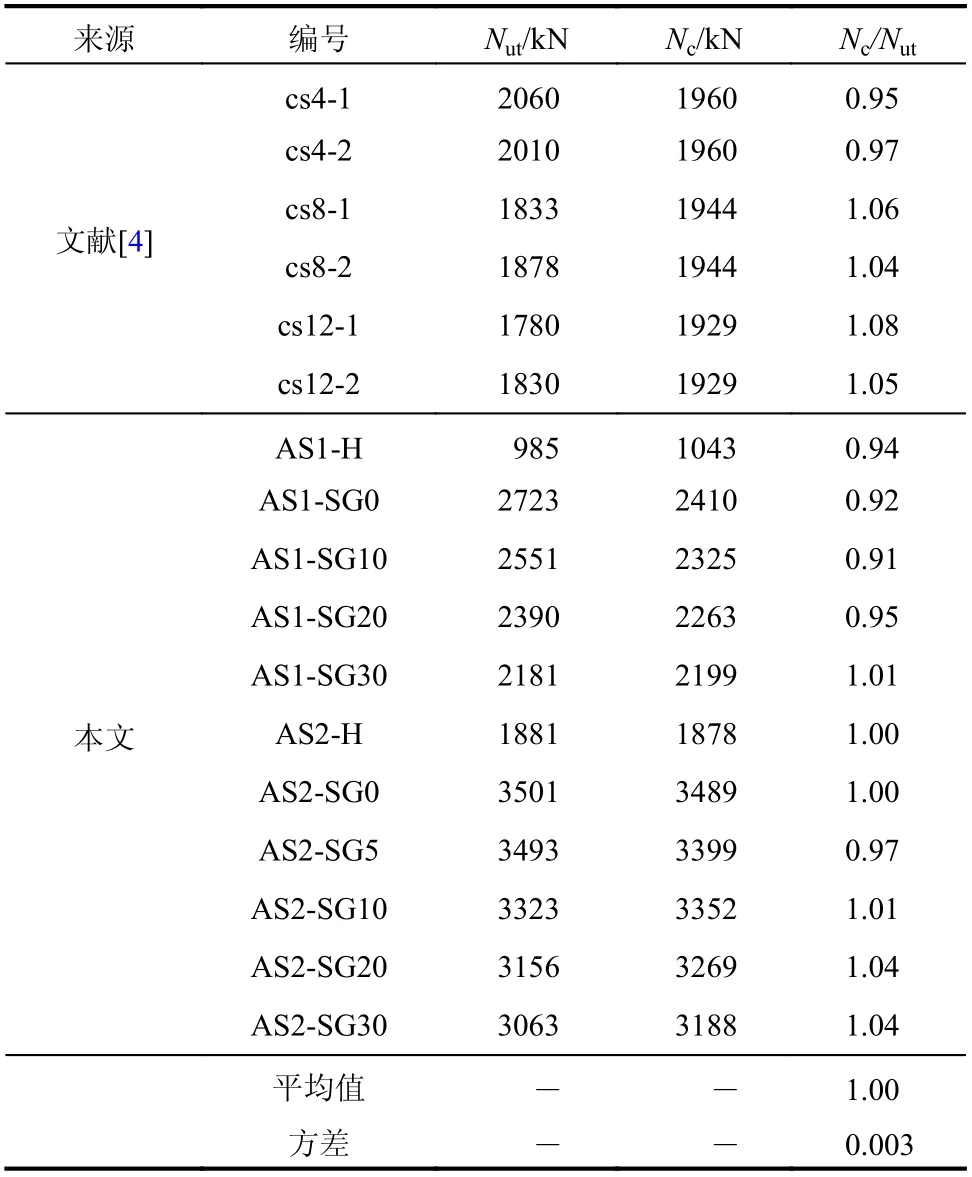
表5 试验结果与计算结果对比Table 5 Comparison between the test and predicted results

5 结论

本文以带球冠形脱空椭圆钢管混凝土轴压短柱为研究对象，通过试验研究和理论分析，得到了以下结论：

(1)由于球冠形混凝土脱空的出现降低了椭圆核心混凝土受压的承载面积和钢管对混凝土的约束作用，导致椭圆钢管混凝土短柱的轴压承载力和初始刚度均出现较大程度的削弱，且随着球冠形脱空率的增大会加剧椭圆钢管混凝土短柱的轴压承载力和初始刚度降低的损失程度；

(2)球冠形脱空缺陷的存在使得脱空区钢管缺乏混凝土的支撑作用，混凝土缺乏钢管的有效约束以及截面形心轴与轴压荷载出现初始偏移，进而导致试件出现脱空区钢管的局部鼓曲与凹陷、脱空侧混凝土的脆性破碎和试件倾向于脱空侧的整体轻微弯曲等破坏模式；

(3)带球冠形脱空椭圆钢管混凝土轴压短柱的延性系数随着钢材强度的提高而增大，随着脱空率的增大而减小；

(4)基于脱空特征系数分析可知：球冠形脱空的增大一方面减小了核心混凝土的受力面积，还会显著削弱钢管对核心混凝土的约束作用，进而降低短柱试件的轴压承载能力和延性；

(5)本文基于核心混凝土约束分区模型，提出了考虑椭圆截面特征和球冠形脱空影响的带球冠形脱空椭圆钢管混凝土短柱的轴压承载力评估及预测方法，并通过试验结果对比，验证了本文计算公式的准确性和可靠性。