地震作用下桥墩动水压力及Morison 方程适用性试验研究
吴 堃,李忠献
(1. 天津大学滨海土木工程结构与安全教育部重点实验室,天津 300350;2. 中国民航大学交通科学与工程学院,天津 300300)
深水桥梁结构可能同时承受地震和水动力的耦合作用。水与桥墩之间的动力相互作用主要体现为水对桥墩的动水压力,该动水压力会对结构的动力特性和地震响应产生较大影响。水与桥墩动力相互作用是典型的流固耦合振动问题,其作用机理十分复杂。目前,研究水—桥墩相互作用的方法主要有Morison 方程、辐射波浪理论、数值法和水下振动台试验法。
Morison 方程是一种半经验半理论的计算方法,假定结构的存在不影响波浪的运动,认为结构受到的波浪力主要包括水平的惯性力和粘滞阻尼力。Morison 方程最初由MORISON 等[1]提出,用于计算小直径柱体受到的水平波浪力,之后PENZIEN 和KAUL[2]将其应用于计算地震作用下小直径柱体受到的动水压力。YANG 和LI[3]提出能够同时计算小尺寸圆形、矩形空心墩柱动水压力的扩展Morison 方程,该公式可以计算墩柱内域和外域的动水压力。KEULEGAN 和CARPENTER[4]、俞聿修[5]、张宁川等[6]深入研究了Morison 方程中惯性力系数和阻尼力系数的取值和变化规律。崔俊男和董胜[7]建立了内孤立波对Spar 平台的水平力理论计算模型。辐射波浪理论以水体速度势作为基本变量,结合一定的边界条件求解流体控制方程,得到动水压力的解答,其适用性广但求解复杂。LIAW 和CHOPRA[8]最早基于辐射波浪理论推导了水中悬臂结构的动水压力。GOYAL 和CHOPRA[9]基于辐射波浪理论,提出了计算空心柱体内、外域动水附加质量的简化方法。CHOPRA等[10− 11]利用辐射波浪理论,考虑库底柔性介质、坝基岩石柔性等因素,研究了动水压力对坝体地震响应的影响。赖伟等[12− 13]基于辐射波浪理论和分离变量法建立了圆形桥墩和桩基承台的动水压力解答,并提出了非圆柱体等效为圆柱体的近似处理方法。黄信和李忠献[14− 15]基于辐射波浪理论建立了考虑水底柔性反射边界、自由表面波和水体压缩性的动水压力表达式,并分析了三者对地震动水压力的影响。WANG等[16− 19]基于辐射波浪理论,分别建立了矩形、圆形、椭圆形和圆锥形等不同形状桥墩地震动水压力的简化计算公式。郭婕等[20]从频域传递函数的角度,对辐射波浪理论、Morison 方程等方法进行了对比分析。数值法主要是利用有限元法或边界元法进行求解。SHARAN[21]基于有限元法,忽略水体压缩性,考虑自由表面波效应,建立了一种非常有效的非扰动边界条件。WILLIAMS[22]利用圆柱体的对称性,将边界积分方法中的三维问题转化为一维问题,研究了动水压力对圆柱结构地震响应的影响。BATHE 等[23]采用ADINA 软件,考虑水体压缩性、大变形、非线性响应和接触条件等的影响,建立了一种高效的水—结构耦合分析方法。水下振动台试验法是指通过水下振动台试验研究不同工况下桥墩受到的动水压力。TANAKA 和HUDSPETH[24]分别对刚性低矮圆柱和柔性细长圆柱结构进行了水下振动台试验,得到了柱体上总动水力及动水压力的分布规律。宋波等[25]以长江三桥群桩基础为原型,进行了水箱振动台试验,研究了模型在正弦波激励及地震激励下的动水压力分布。黄信[26]采用水箱振动台试验研究了水底柔性介质对桥墩地震动水压力的影响,结果表明水底柔性介质会使动水压力有一定减小,但总体来讲可以忽略其影响。DING 等[27]通过水下振动台试验研究了地震动水压力的分布规律及其对桥梁动力响应的影响规律。
Morison 方程因其概念简单,计算方便,广泛用于计算桥墩地震动水压力。需要指出的是,Morison 方程是半经验半理论公式,由波浪力的计算公式演化而来,用于计算地震动水压力还缺乏一定的理论基础和试验验证。惯性力系数和阻尼力系数的取值均通过波浪试验确定,用于计算地震动水压力同样缺乏相应的验证。同时,目前采用水下振动台试验法研究桥墩地震动水压力的研究较少,鲜见相关文献通过试验系统研究试件、水深、激励特性等对桥墩地震动水压力的影响。
为解决上述问题,本文利用一个大型水箱和伺服作动器搭建了一套水下振动台试验系统,以不同尺寸桥墩为研究对象,采用正弦波作为输入激励,分别研究不同直径、不同水深、不同激励幅值和不同激励频率对桥墩加速度和动水压力的影响规律,并通过试验验证地震作用下Morison 方程的适用性。
1 试验设计
1.1 试验设备
试验在北京博科测试系统股份有限公司的简易“水下振动台”上进行。该简易“水下振动台”是为验证天津大学研制的世界上首台水下地震模拟振动台台阵系统的试验性能所设计的专门装置,如图1所示。水箱尺寸为5.2 m×5.2 m×1.2 m,支撑在4 个钢立柱上。振动台台体采用30 mm 厚钢板,圆形台面直径900 mm,台体与水箱底板之间间隙为125 mm,采用防水布连接;作动器采用Servotest 080-150-25 型,最大行程±75 mm,工作频率0.1 Hz~100 Hz。作动器一端与台体相连,另一端固定在底座上。作动器驱动台体在固定于底部钢框架上的2 个平行导轨上水平运动,导轨采用工业级导轨,底部框架采用支撑框架,从而保证了试验精度。

图1 水下振动台试验系统Fig. 1 Underwater shaking table test system
1.2 试件设计
对于深水桥梁结构,尤其是大型跨海、跨江桥梁,桥墩的尺寸和配筋率较大,桥墩刚度较大。因此,本文为了方便试验,采用4 个圆形钢管作为试件,尺寸(直径×壁厚)分别为101 mm×10 mm、150 mm×10 mm、324 mm×12.5 mm 和610 mm×16 mm,试件高度均为1.2 m,如图2 所示。根据文献[23],当试件尺寸与水箱尺寸之比小于1/5 时,水域影响较小。本试验中,振动方向试件最大直径与水箱长度之比约为1/8.5,水域影响很小,水箱边界条件对试验结果的影响可以忽略。

图2 不同尺寸的试件Fig. 2 Specimens with different dimensions
1.3 测点布置
试件测点布置如图3 所示,采用11 个加速度传感器和11 个动水压力传感器。图中A 代表加速度传感器,布置在试件的背水面;P 代表动水压力传感器,布置在试件的迎水面。加速度传感器采用日本TML 公司生产的ARH-100A 型水下加速度传感器,量程为10g;动水压力传感器由中交天津港湾工程研究院生产,量程为30 kPa。
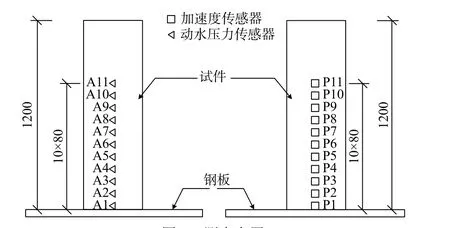
图3 测点布置 /mmFig. 3 Layout of measuring points
1.4 试验工况
为了研究不同水深、不同激励频率以及不同激励幅值时桥墩加速度和动水压力的变化规律,试验采用正弦波激励,如表1 所示,正弦波激励频率分别为1 Hz、2 Hz、4 Hz、7 Hz 和10 Hz,激励幅值分别为0.1g、0.2g、0.4g、0.7g和1.0g,水深分别为0.2 m、0.5 m 和0.8 m。因此,每个试件共有75 个试验工况。需要说明的是,所有钢管试件的固有频率均大于50 Hz,试验所用正弦波的频率均在共振频率范围之外。
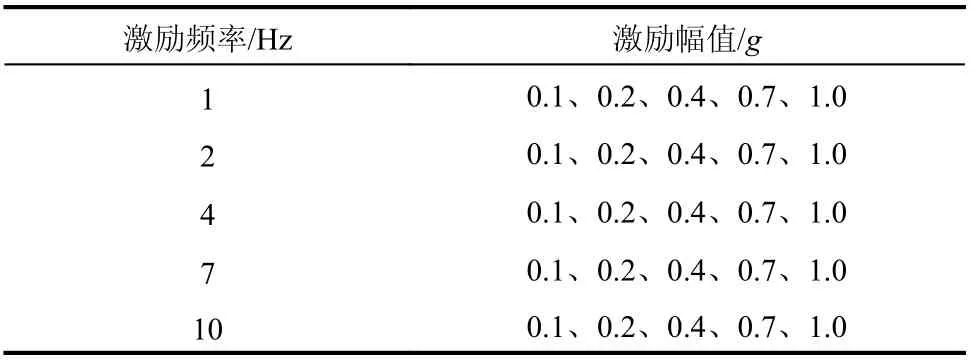
表1 正弦波激励频率和幅值Table 1 Amplitude and frequency of sinusoidal wave
2 试验结果与分析
2.1 不同工况下桥墩加速度变化规律
2.1.1 不同激励幅值下桥墩加速度的变化
图4 为桥墩加速度随激励幅值的变化情况,其中图4(a)为试件直径101 mm、水深0.8 m、激励频率2 Hz 的工况,图4(b)为直径610 mm、水深0.8 m、激励频率10 Hz 的工况。需要说明的是,图4~图7 中桥墩加速度均经过归一化处理,即用桥墩某一高度处加速度绝对值除以墩底加速度。
由图4(a)可知,截面直径、激励频率较小时,加速度沿桥墩高度方向变化较小,激励幅值从0.1g增加到1.0g时,同一高度处桥墩加速度最多相差2.4%,可以忽略。由图4(b)可知,截面直径、激励频率较大时,加速度沿桥墩高度方向变化较大,激励幅值从0.1g增加到1.0g时,同一高度处桥墩加速度最多增大9.3%。因此,不同工况下,桥墩加速度随激励幅值变化规律有所不同,截面直径、激励频率较大时,应考虑激励幅值对桥墩加速度的影响。
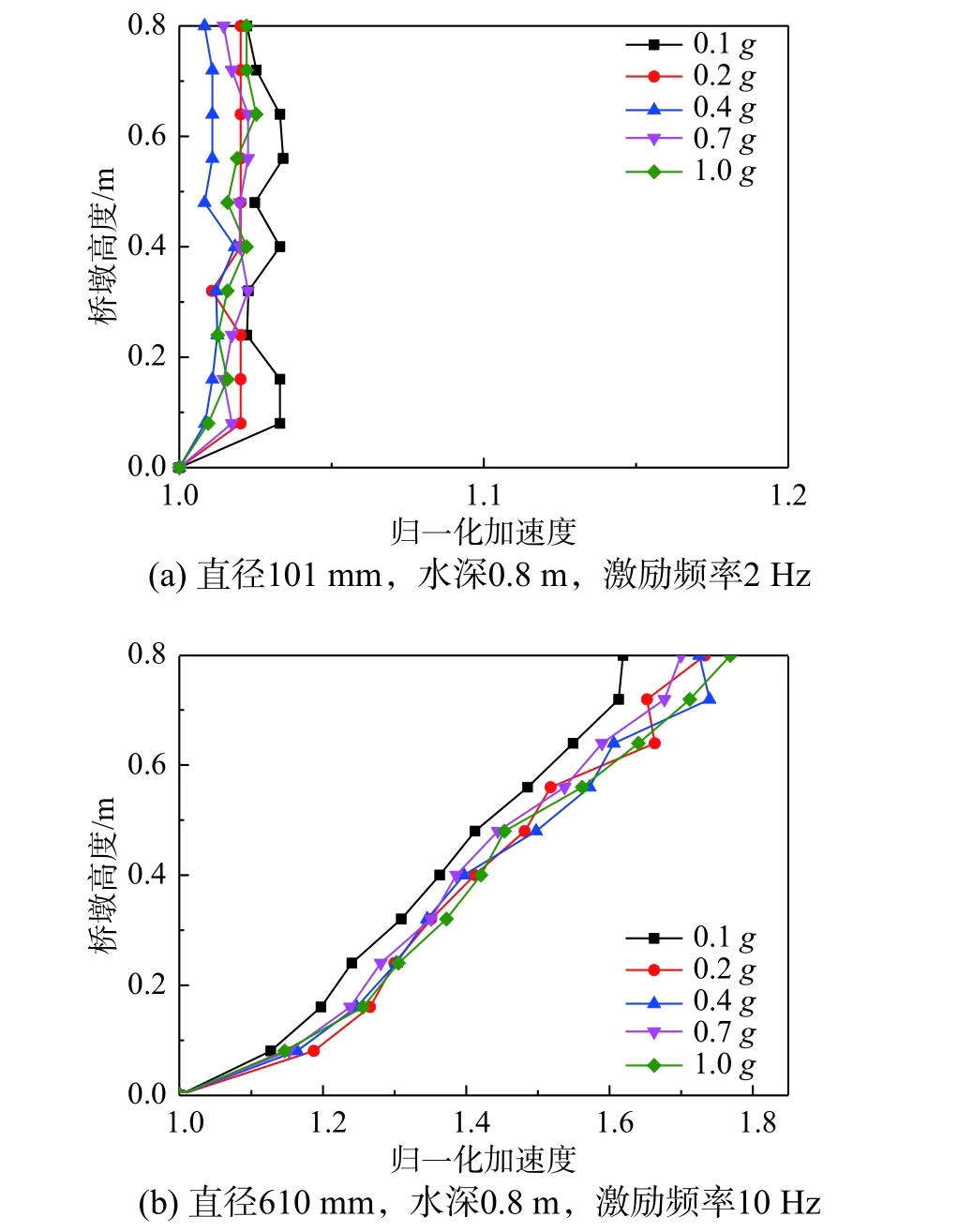
图4 不同激励幅值下桥墩加速度变化规律Fig. 4 Change of acceleration of pier with different excitation amplitudes
2.1.2 不同激励频率下桥墩加速度的变化
图5 为桥墩加速度随激励频率的变化情况,其中图5(a)为试件直径150 mm、水深0.2 m、激励幅值0.1g的工况,图5(b)为直径610 mm、水深0.8 m、激励幅值0.4g的工况,受作动器性能限制,激励频率1 Hz 时激励幅值最大为0.2g。
由图5 可知,同一高度处的桥墩加速度随激励频率增大而增大,激励频率较小时加速度沿桥墩高度几乎没有变化;激励频率较大时加速度由墩底向墩顶逐渐增大,且增大的程度随激励频率增大而增大。这是因为桥墩刚度较大,激励频率较小时,激励频率与桥墩自振频率相差很大,输入激励相当于静力荷载;激励频率较大时,激励频率相对更接近桥墩自振频率,输入激励的动力效应更明显。综合得出,激励频率在4 Hz 以内时,加速度沿桥墩高度变化较小,同一高度处加速度最多增大6.4%;激励频率大于4 Hz时,加速度沿桥墩高度变化较大,同一高度处加速度最多增大72.5%。因此,地震作用下桥墩加速度应考虑激励频率的影响。
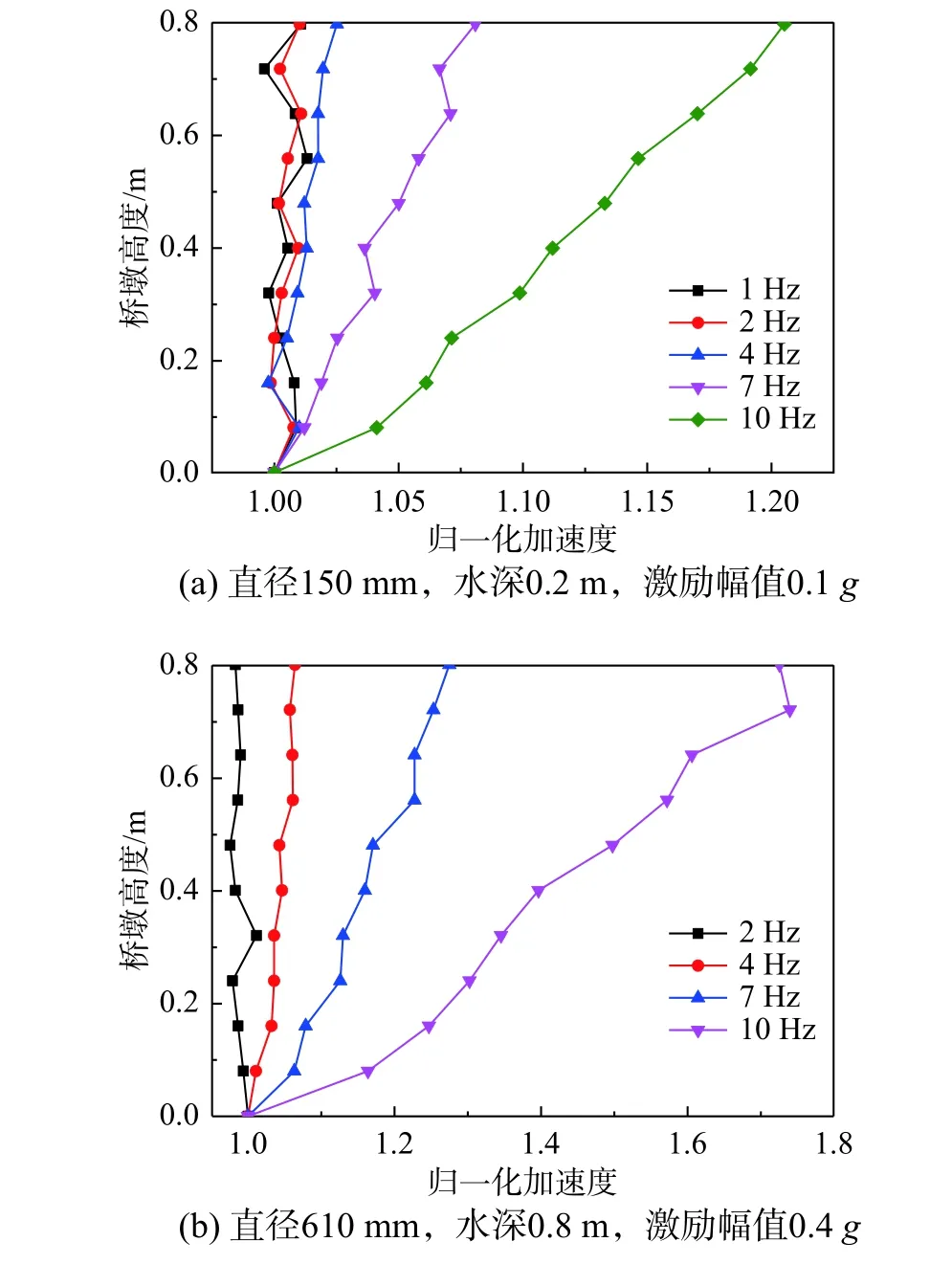
图5 不同激励频率下桥墩加速度变化规律Fig. 5 Change of acceleration of pier with
2.1.3 不同截面直径下桥墩加速度的变化
图6 为桥墩加速度随截面直径的变化情况,其中图6(a)为水深0.2 m、激励频率4 Hz、激励幅值0.2g的工况,图6(b)为水深0.8 m、激励频率10 Hz、激励幅值0.7g的工况。
由图6 可知,随着截面直径的增大,桥墩加速度由墩底向墩顶逐渐增大,增大的程度随截面直径增大而增大,且激励频率、激励幅值越大,增大的程度也越大。这是因为截面直径越大,水—桥墩相互作用产生的附加质量效应越大,对桥墩自振频率的影响越大,相同激励下其动力效应越明显。综合得出,不同工况下,截面直径从101 mm 增大到610 mm,同一高度处桥墩加速度最多增大43.6%。因此,地震作用下桥墩加速度应考虑截面直径的影响。
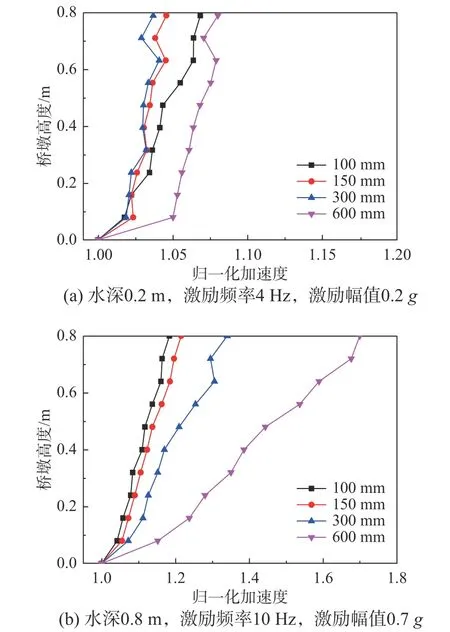
图6 不同截面直径下桥墩加速度变化规律Fig. 6 Change of acceleration of pier with different section diameters
2.1.4 不同水深下桥墩加速度的变化
图7 为桥墩加速度随水深的变化情况,其中图7(a)为截面直径101 mm、激励频率2 Hz、激励幅值0.4g的工况,图7(b)为截面直径324 mm、激励频率4 Hz、激励幅值1.0g的工况。
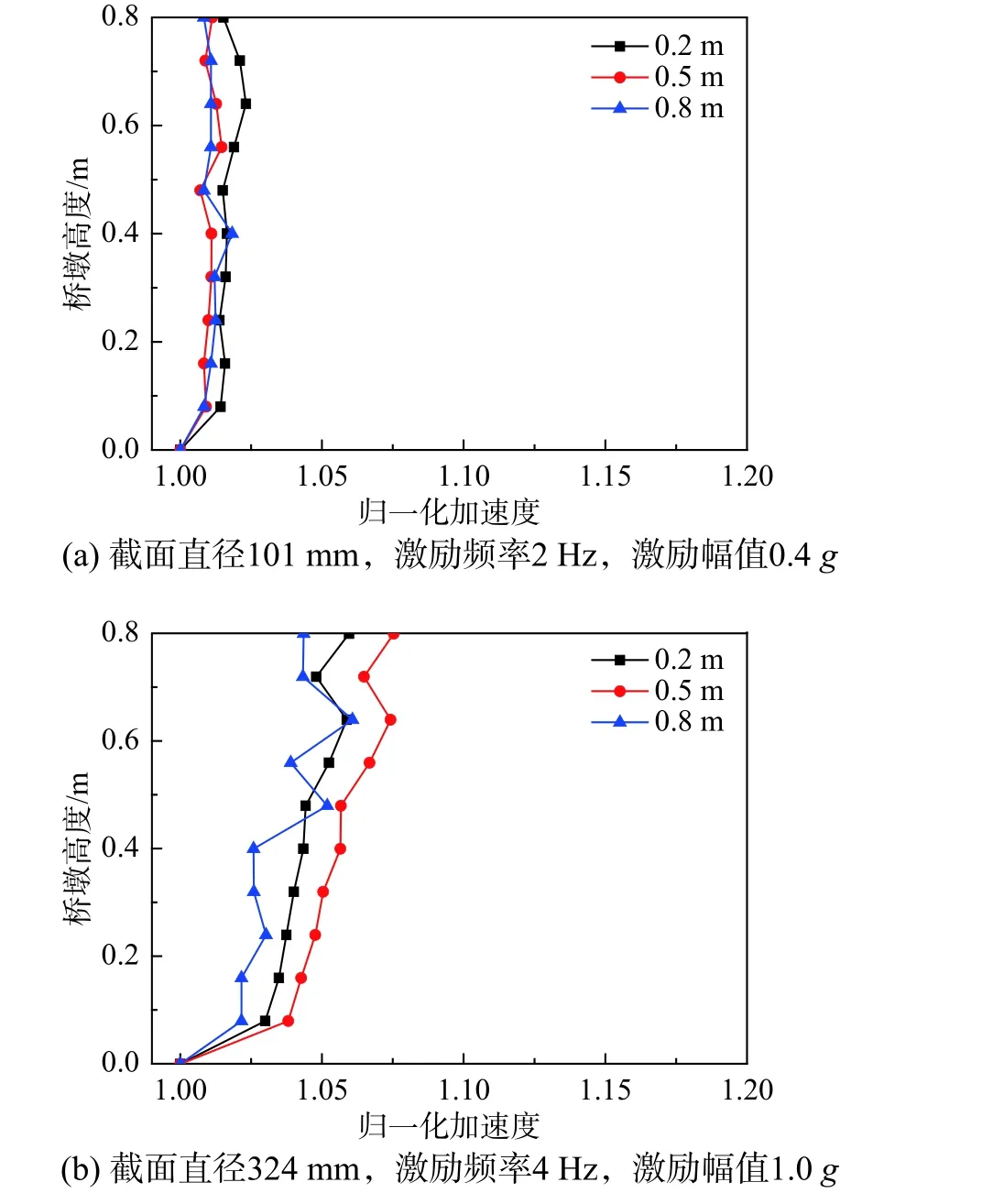
图7 不同水深下桥墩加速度变化规律Fig. 7 Change of acceleration of pier with different water depths
由图7 可知,随着水深的增大,桥墩加速度沿高度的分布规律几乎不变。这是由于水深增大时,水—桥墩相互作用产生的附加质量效应和附加阻尼效应对加速度的影响可以近似抵消。水深从0.2 m增大到0.8 m 时,相同高度处的加速度变化小于5%。因此,地震作用下桥墩加速度受水深影响较小。
2.2 不同工况下桥墩动水压力变化规律
2.2.1 不同激励幅值下桥墩动水压力的变化
图8 为桥墩动水压力随激励幅值的变化情况,其中图8(a)为截面直径101 mm、水深0.5 m、激励频率4 Hz 的工况,图8(b)为截面直径610 mm、水深0.8 m、激励频率10 Hz 的工况。
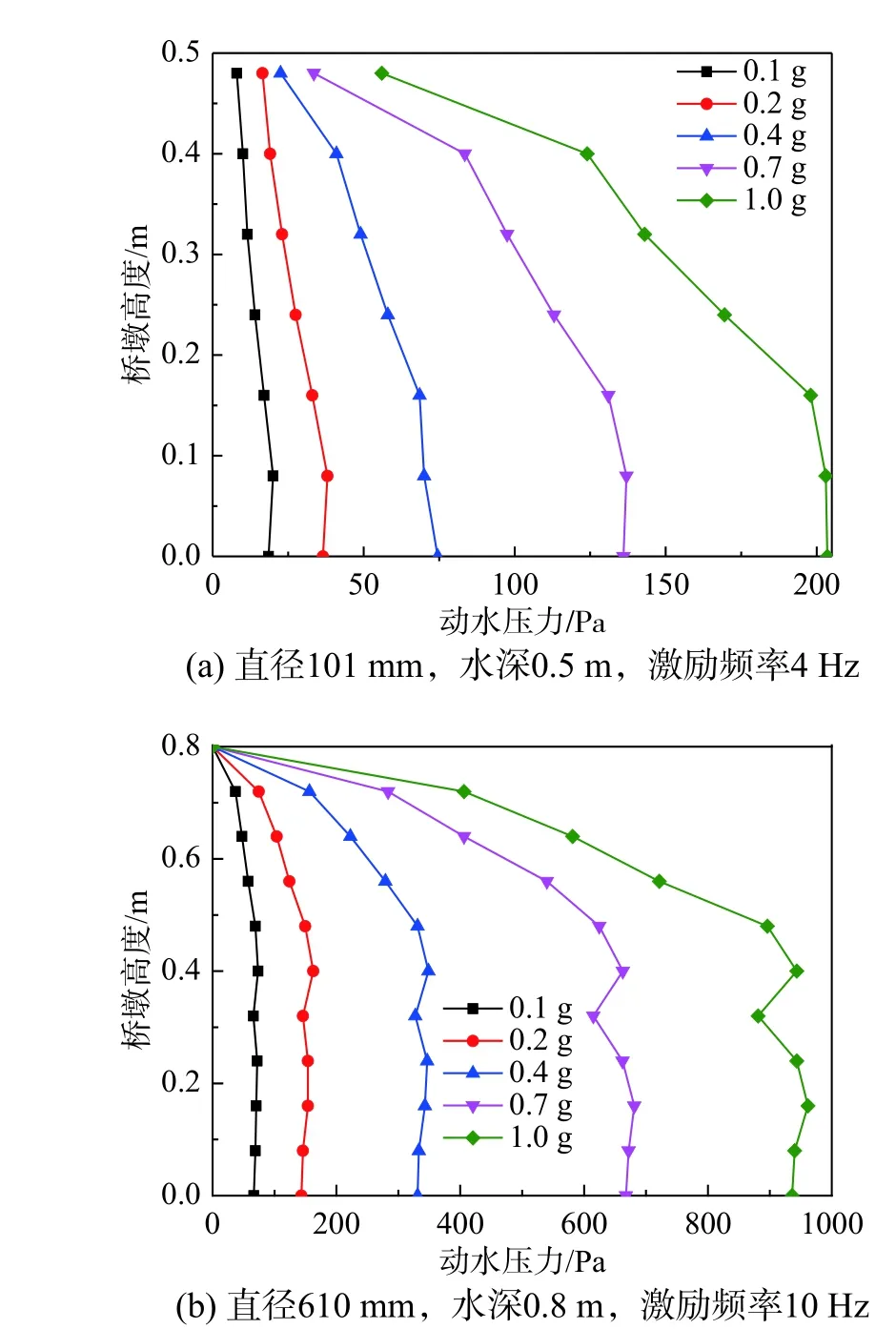
图8 不同激励幅值下桥墩动水压力变化规律Fig. 8 Change of hydrodynamic pressure of pier with different excitation amplitudes
由图8 可知,地震作用下,桥墩动水压力的分布规律为由底部到顶部逐渐减小,水面处接近0;桥墩不同高度处动水压力随激励幅值增大而增大。这是因为相同工况时,激励幅值越大,水—桥墩相互作用越强,动水压力也越大。综合得出,不同工况下,激励幅值从0.1g增大到1.0g时,墩底动水压力增大10.0 倍~13.1 倍。因此,地震作用下桥墩动水压力应考虑激励幅值的影响。
2.2.2 不同激励频率下桥墩动水压力的变化
图9 为桥墩动水压力随激励频率的变化情况,其中图9(a)为截面直径101 mm、水深0.8 m、激励幅值1.0g的工况,图9(b)为截面直径610 mm、水深0.8 m、激励幅值0.4g的工况。
由图9 可知,不同工况下,桥墩动水压力随激励频率变化规律不同。由图9(a)可知,动水压力随激励频率先减小后增大,激励频率从2 Hz 增大到7 Hz 时,墩底动水压力减小了55%,激励频率从7 Hz 增大到10 Hz 时,墩底动水压力增大了67.7%;由图9(b)可知,动水压力随激励频率先增大后减小,激励频率从2 Hz 增大到7 Hz 时,墩底动水压力增大了29.8%;激励频率从7 Hz 增大到10 Hz 时,墩底动水压力减小了32.7%。因此,地震作用下桥墩动水压力应考虑激励频率的影响。
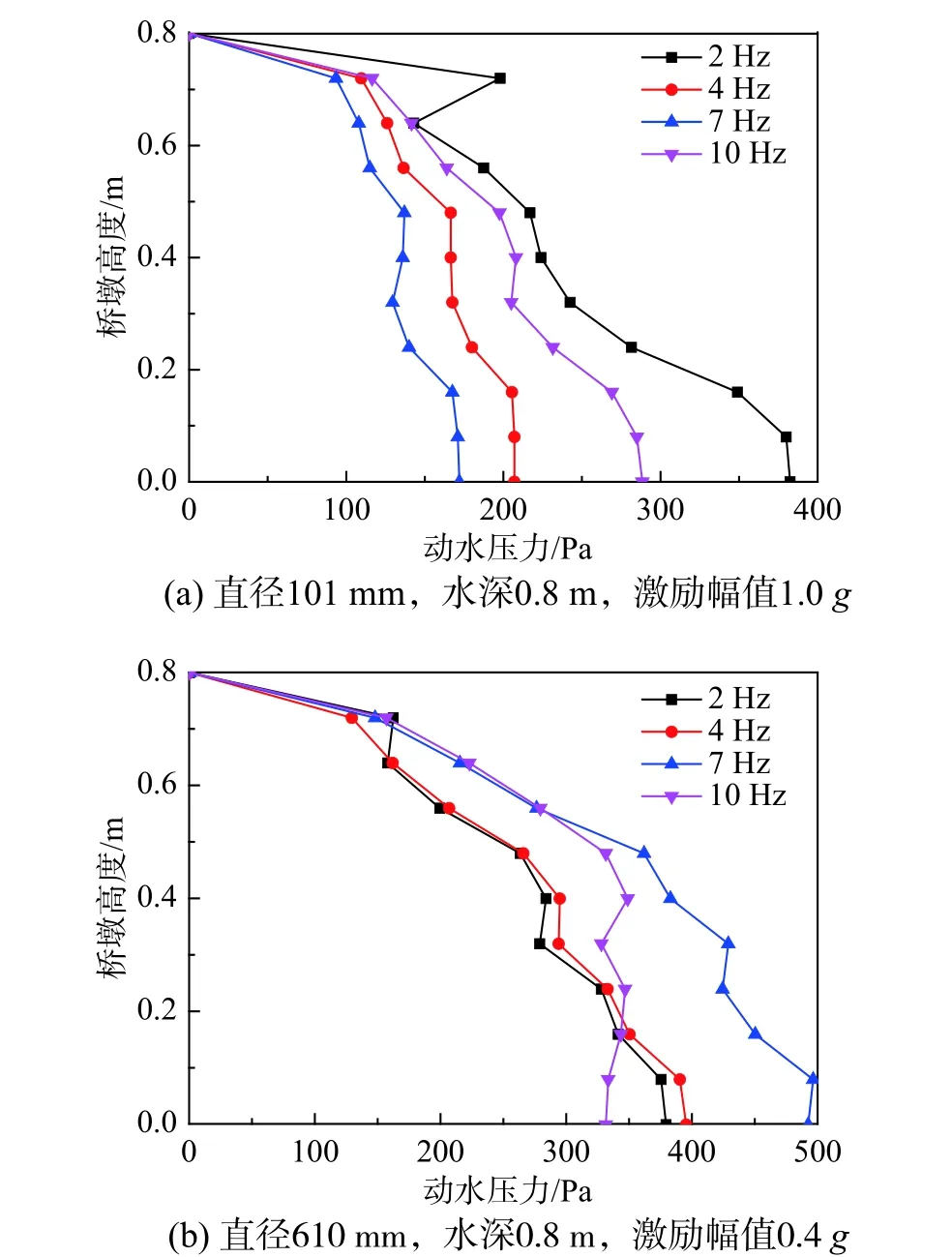
图9 不同激励频率下桥墩动水压力变化规律Fig. 9 Change of hydrodynamic pressure of pier with different excitation frequencies
2.2.3 不同截面直径下桥墩动水压力的变化
图10 为桥墩动水压力随截面直径的变化情况,其中图10(a)为水深0.5 m、激励频率4 Hz、激励幅值0.2g的工况,图10(b)为水深0.8 m、激励频率10 Hz、激励幅值0.7g的工况。
由图10 可知,不同工况下,桥墩动水压力随截面直径增大而增大,不同高度处动水压力与截面直径基本成正比。这是因为相同工况时,截面直径越大,水体与结构的接触面越大,水—桥墩相互作用越强,动水压力也越大。综合得出,不同工况下,截面直径从101 mm 增大到610 mm时,墩底动水压力增大2.5 倍~3.5 倍。因此,地震作用下桥墩动水压力应考虑截面直径的影响。
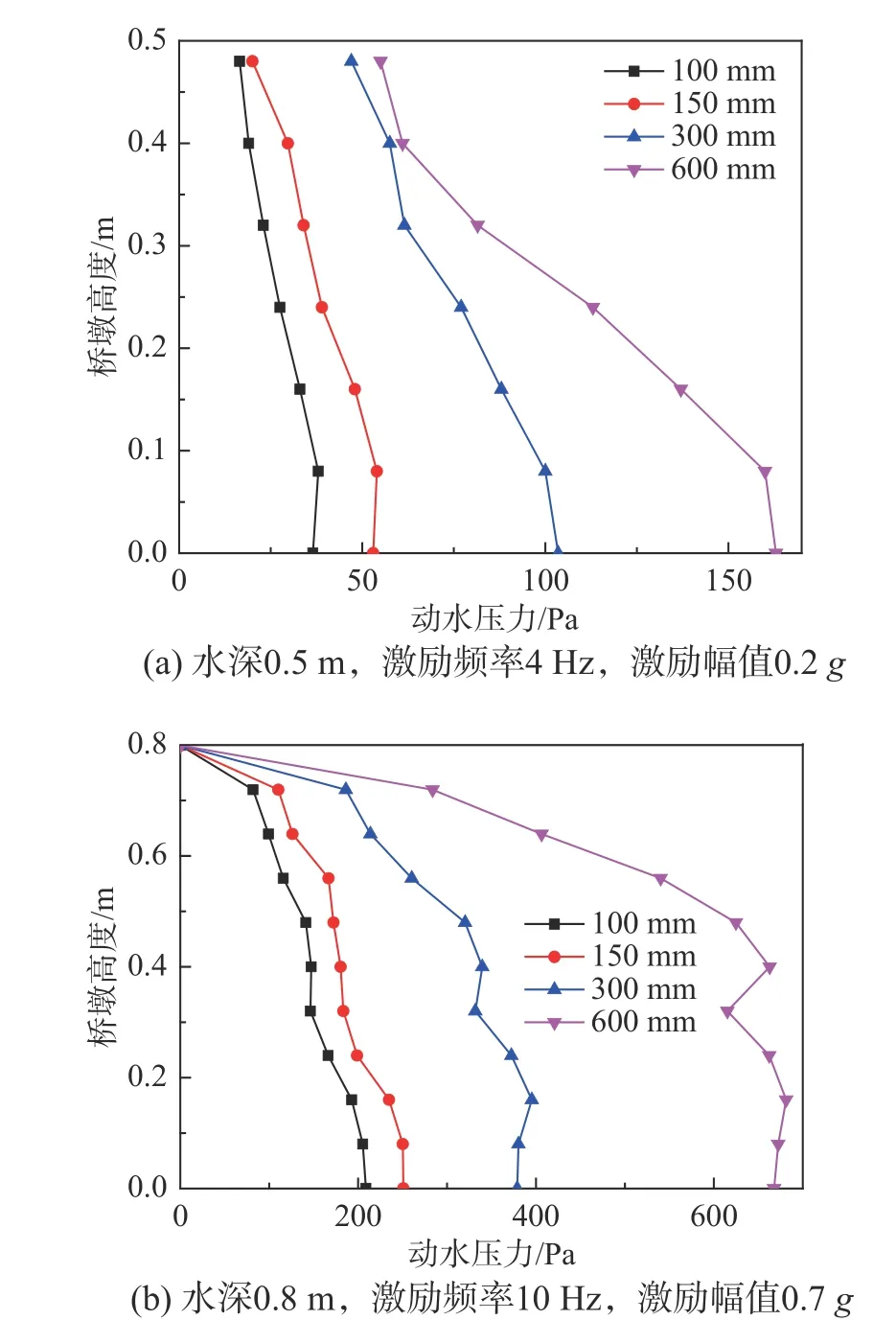
图10 不同截面直径下桥墩动水压力变化规律Fig. 10 Change of hydrodynamic pressure of pier with different section diameters
2.2.4 不同水深下桥墩动水压力的变化
图11 为桥墩动水压力随水深的变化情况,其中图11(a)为截面直径150 mm、激励频率4 Hz、激励幅值0.2g的工况,图11(b)为截面直径610 mm、激励频率10 Hz、激励幅值0.7g的工况。
由图11 可知,不同工况下,桥墩动水压力随水深增大而增大。这是因为相同工况时,水深越大,水体与结构的接触面越大,水—桥墩相互作用越强,动水压力也越大。综合得出,不同工况下,水深从0.2 m 增大到0.8 m 时,墩底动水压力增大1.5 倍~2.1 倍。因此,地震作用下桥墩动水压力应考虑水深的影响。
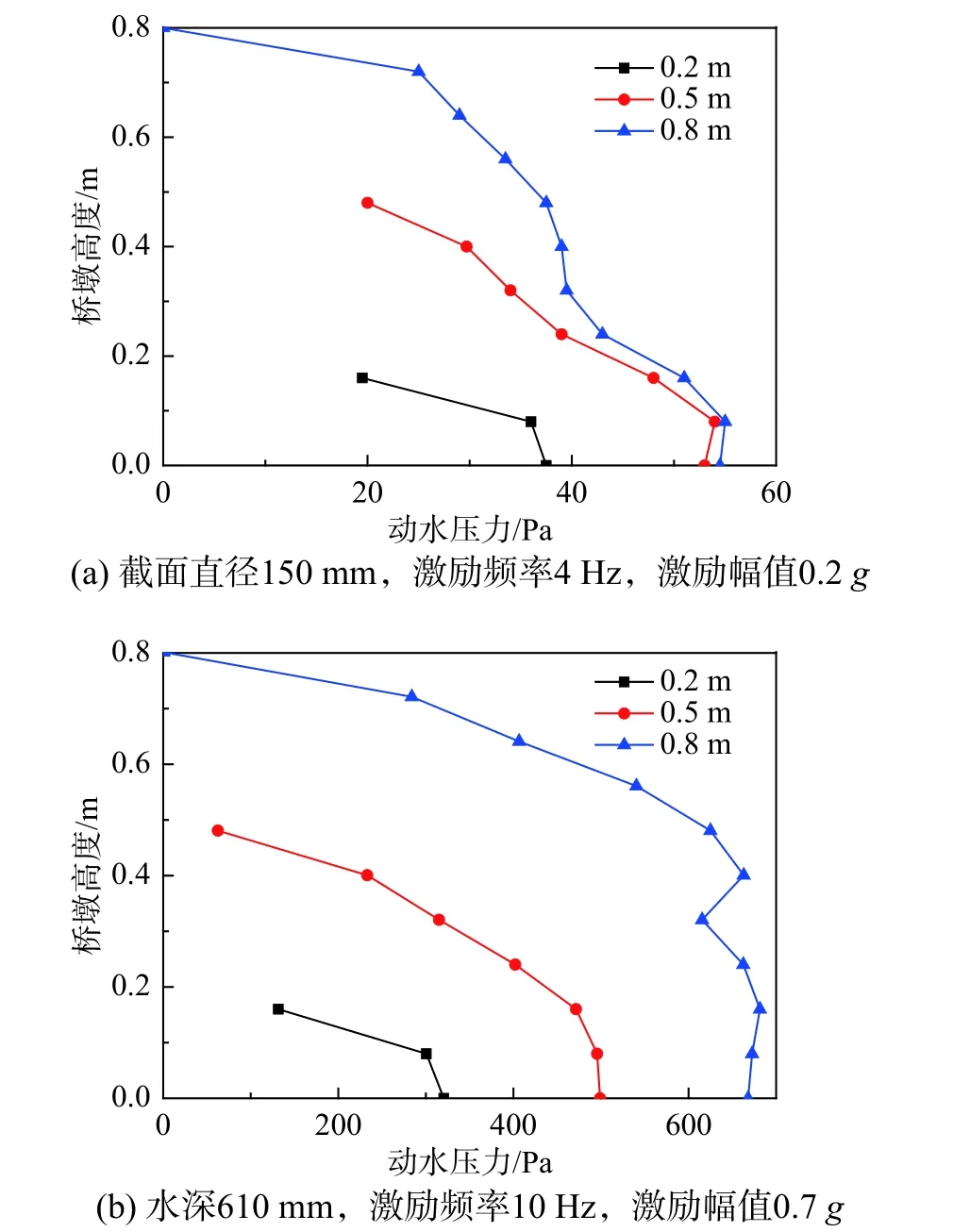
图11 不同水深下桥墩动水压力变化规律Fig. 11 Change of hydrodynamic pressure of pier with different water depths
2.3 地震作用下Morison 方程适用性
对于深水桥梁结构,地震作用下桥墩某一点处动水压力可表示为[28]:
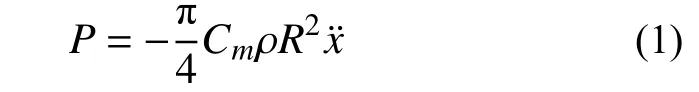
式中:ρ 为水体密度;R为桥墩迎水面宽度;ẍ为桥墩绝对加速度;Cm为惯性力系数,对于圆形桥墩取常数1.0。
由式(1)可知,地震作用下桥墩一点处动水压力与迎水面宽度的平方成正比,与该点处加速度成正比,与激励频率、激励幅值、水深等没有直接关系。然而,本文通过试验发现,地震作用下桥墩动水压力随激励幅值、截面直径、水深增大而增大,随激励频率变化较大,且不同工况下桥墩动水压力与截面直径的平方并不是正比关系。
图12 给出了不同工况下Morison 方程计算结果与试验结果的对比,其中Morison 方程中的加速度采用试验测得的加速度。图12(a)为截面直径100 mm、水深0.8 m、激励频率4 Hz、激励幅值0.4g的工况,图12(b)为截面直径100 mm、水深0.8 m、激励频率7 Hz、激励幅值0.4g的工况,图12(c)为截面直径600 mm、水深0.8 m、激励频率7 Hz、激励幅值0.4g的工况,图12(d)为截面直径600 mm、水深0.8 m、激励频率7 Hz、激励幅值1.0g的工况。由图12 可知,Morison 方程计算的桥墩动水压力与试验结果相差较大;Morison方程认为动水压力的分布与桥墩加速度分布相同,而试验结果显示桥墩动水压力从下到上逐渐减小。截面直径较小时,Morison 方程低估了桥墩动水压力,Morison 方程计算的墩底动水压力小于试验结果的1/2;截面直径较大时,Morison 方程高估了桥墩动水压力,Morison 方程计算的墩底动水压力是试验结果的2 倍以上。
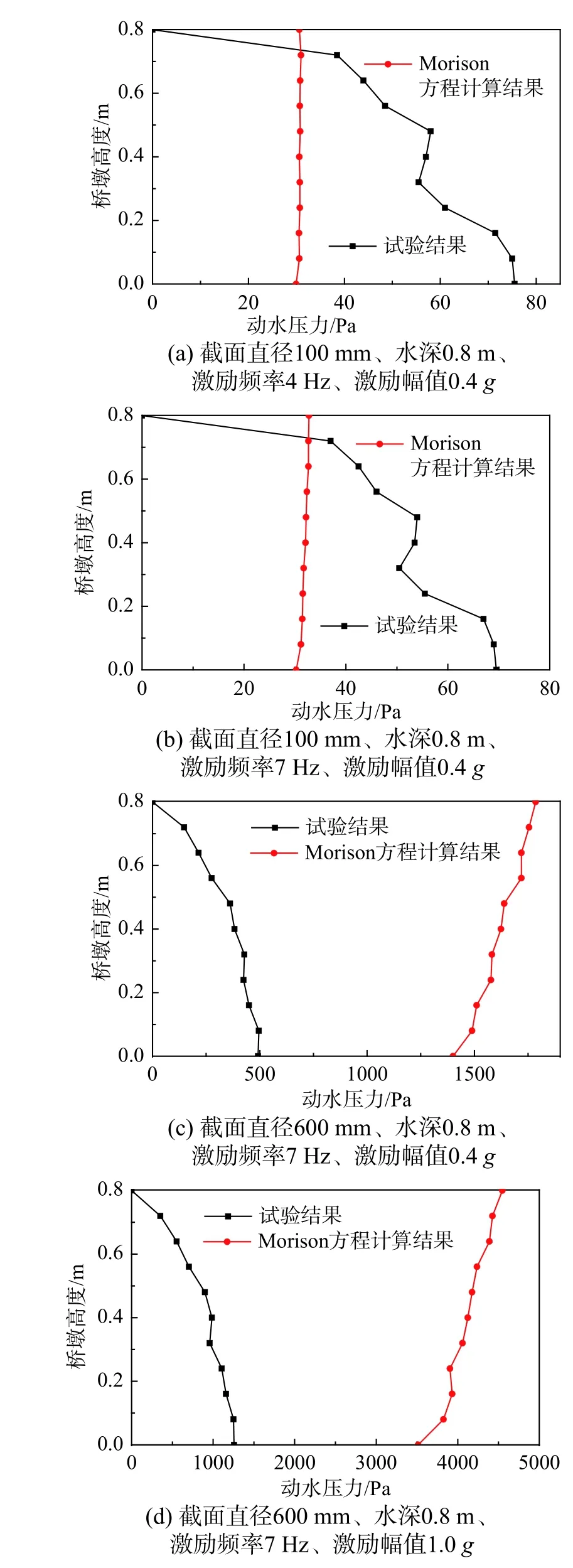
图12 Morison 方程计算结果与试验结果对比Fig. 12 Results of Morison equation compared with test results
综上可知,无论是桥墩动水压力的分布规律,还是不同工况下动水压力的数值,Morison 方程均不适用于计算地震作用下桥墩的动水压力。究其原因应是Morison 方程中惯性力系数是通过波浪力试验确定的,而波浪力与地震作用的产生机制、作用特性等相差较大,通过波浪力试验所确定的惯性力系数不适用于计算地震动水压力。因此,应通过大量的水下振动台试验,进一步确定地震动水压力的惯性力系数。
3 结论
本文以深水桥墩为研究对象,通过对4 个钢管试件进行水下振动台试验,系统研究了不同激励幅值、激励频率、截面直径和水深下桥墩地震动水压力的变化规律,得出以下结论:
(1)地震作用下桥墩加速度应考虑激励幅值、激励频率和截面直径的影响,受水深影响较小。不同工况下,桥墩加速度随激励幅值最多增大9.3%,随激励频率最多增大72.5%,随截面直径最多增大43.6%,随水深变化在5%以内。
(2)地震作用下桥墩动水压力应考虑激励幅值、激励频率、截面直径和水深的影响。不同工况下,桥墩动水压力随激励幅值最多增大13.1 倍,随激励频率最多增大67.7%,随截面直径最多增大3.5 倍,随水深最多增大2.1 倍。
(3)地震作用下,Morison 方程不能准确描述桥墩动水压力沿高度的分布规律,计算得到的桥墩动水压力与试验结果相差较大,Morison 方程不适用于计算地震作用下桥墩动水压力,应通过大量的水下振动台试验加以修正。

