附加旋转圆柱的涡激振动发电装置水动力特性研究

丁广佳，及春宁，徐晓黎，许栋，吕迎雪

（1.中交天津港湾工程研究院有限公司，天津 300222；2.天津大学水利工程仿真与安全国家重点实验室，天津 300072；3.中交第一航务工程局有限公司，天津 300456；4.中国交建海岸工程水动力重点实验室，天津 300222）

1 研究背景

我国沿岸海流资源丰富，可为社会经济发展提供充足且廉价的清洁能源[1]。然而，我国沿岸海流流速普遍偏低（＜1.5 m/s），使得起动流速较高（＞2.0 m/s）的传统海流能利用装置（如涡轮机、水下风车等）的应用受到限制。新型VIVACE（Vortex Induced Vibration Aquatic Clean Energy）海流能利用装置[2]利用柱体在海流作用下的涡激振动俘获海流能，与波浪能利用装置[3]相比，具有能量可利用时间长的特点，并且其起动流速低（0.25 m/s）、能量密度高、结构简单可靠、维护费用低[2]，具有十分突出的经济效益和社会价值，符合我国“双碳目标”的发展战略。

目前，国内外多位学者针对VIVACE的能量利用效率优化开展了许多富有成效的研究工作[4-6]，并应用被动流动控制[7-9]和主动流动控制[10-12]显著提高了VIVACE的振幅和流速响应区间。与被动流动控制相比，主动流动控制可根据装置所处的实时水动力环境动态调整控制策略，使得VIVACE海流能利用装置时刻处于最优俘能状态。及春宁等[13]应用主动流动控制，提出了一种附加旋转圆柱的涡激振动发电装置，如图1所示。该装置可主动调整附加圆柱的转动，控制主圆柱周围的流态，以增大圆柱的振幅和流速响应区间，提高一级能量利用效率。然而，实际海洋环境恶劣多变，在优化其工作性能的同时，也必须考虑其生存性问题。为此，本文针对附加旋转圆柱的涡激振动发电装置的水动力特性进行研究，为其合理设计提供必要的理论指导。

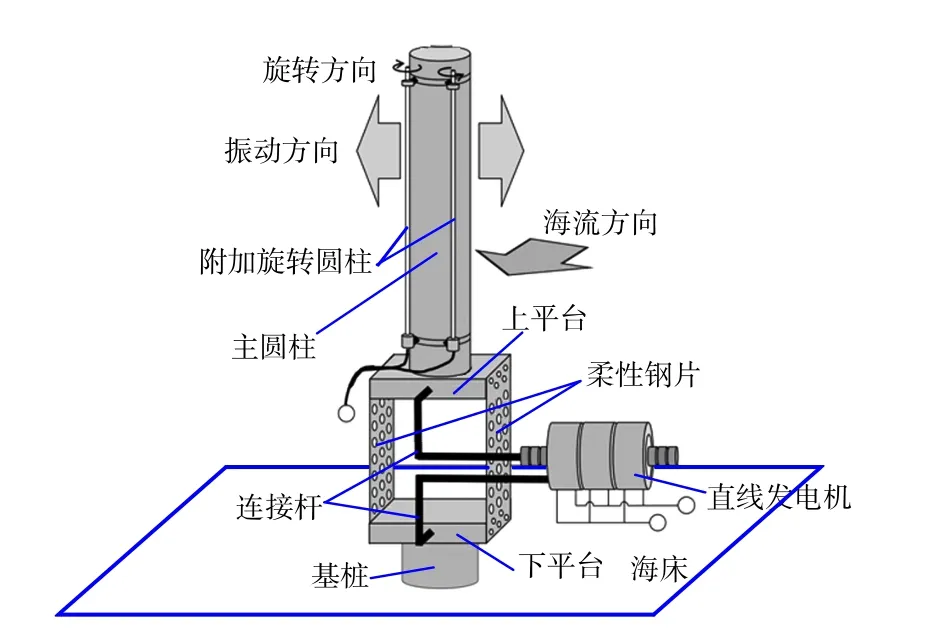
图1 附加旋转圆柱的主动流动控制涡激振动发电装置Fig.1 Vortex-induced vibration energy harvester with active flow control by using attached spinning cylinders

本文对及春宁等[13]提出的发电装置进行二维简化，采用浸入边界法模拟带有两个附属旋转圆柱的振动系统的涡激振动响应，在俘能阻尼比ζharness，附加圆柱无量纲转速α和方位角θ构成的多参数空间内，分析系统的受力和振动幅值。

2 数值模拟方法

采用嵌入式迭代的浸入边界法[14]对流固耦合问题进行数值模拟，控制方程如下：

式中：u为速度矢量；t为时间；p为压强；ρ为流体密度；ν为运动黏滞系数；为梯度算子；上标T为矩阵转置；f为附加体积力矢量，代表流固耦合边界条件。本文针对层流条件下附加旋转圆柱的涡激振动发电装置水动力特性开展研究，因此控制方程中无紊流模型。

对以上控制方程采用二阶的Admas-Bashforth时间格式进行离散，可得守恒形式如下：

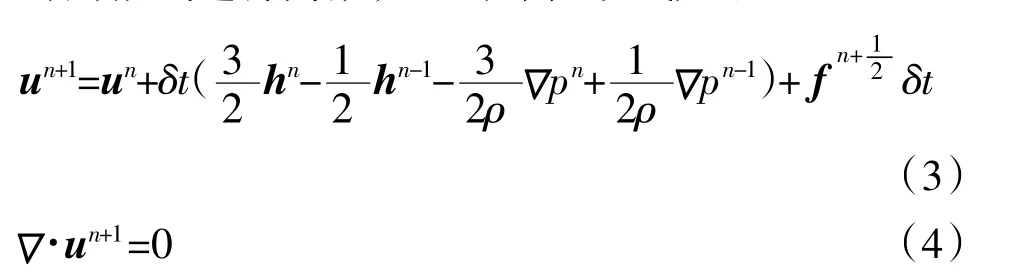
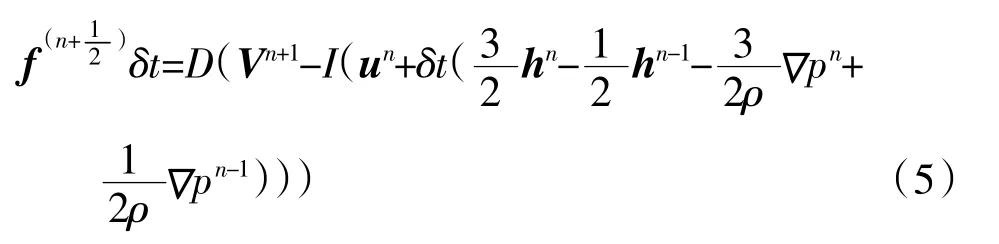
式中：I和D为插值函数；Vn+1为物面边界点的速度矢量。

对做横流向振动的刚性圆柱，其运动方程可表示为：

式中：y为圆柱的横流向振动位移；m为整个振动系统（包含主圆柱和附加圆柱）的质量；c为系统阻尼，包含发电机俘能阻尼charness和结构阻尼cstructure；k为弹簧刚度系数；Fy为系统受到的横向流体力。方程采用标准的Newmark-β法求解。

3 问题描述和模型验证

如图2所示，主圆柱的直径为D，两个对称布置的附加圆柱（C1和C2）的直径均为d，方位角为θ（主圆柱与附加圆柱中心连线与水平方向的夹角），主圆柱与附加圆柱的间隙为g，附加圆柱的无量纲转动速度为α=Usurf/U∞，其中Usurf为附加圆柱表面线速度，U∞为均匀来流流速。规定：图2中附加圆柱的旋转方向（内向转动）为正，反之（外向转动）为负。俘能阻尼比ζharness=charness/（4πm fn），其中fn为系统固有频率。为了获得更高的能量利用效率，本文取cstructure=0。基于主圆柱直径的雷诺数为Re=U∞D/ν=100，质量比为m*=m/mf=2.0，其中mf为系统等体积流体质量。

计算域大小为100D×100D，如图2所示。为保证数值精度，在圆柱周围采用加密网格，加密区域为8D×8D，无量纲网格尺寸为Δx/D=Δy/D=1/64。边界条件设置：入口为Dirichlet型边界（u=U∞，v=0），出口为Neumann型边界（∂u/∂x=0，∂v/∂x=0），上下为可滑移边界（∂u/∂y=0，v=0）。

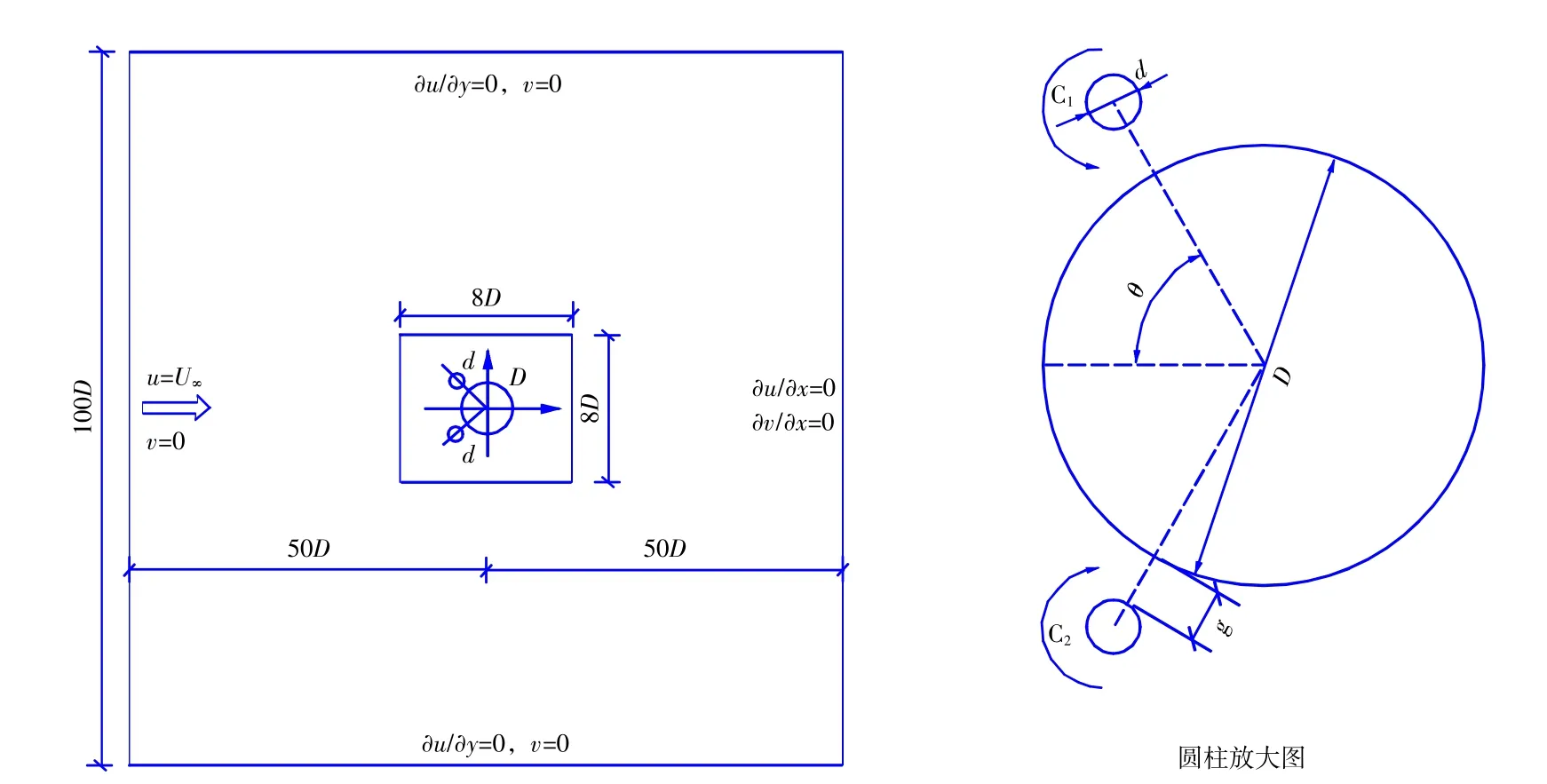
图2 计算域、边界条件和圆柱布置Fig.2 Computational domain,boundary conditions and cylinder configuration

为了验证数值方法的正确性，本文开展了带附加圆柱的单圆柱涡激振动数值模拟，并与Mittal[15]的数值结果对比。数值模拟参数：雷诺数为Re=100，附加圆柱与主圆柱的直径比为d/D=1/20，方位角θ=60°，间隙比g/D=0.075，无量纲转速α=2.0。如表1所示，本文结果与Mittal[15]的计算结果吻合较好，两者差别小于等于5%。

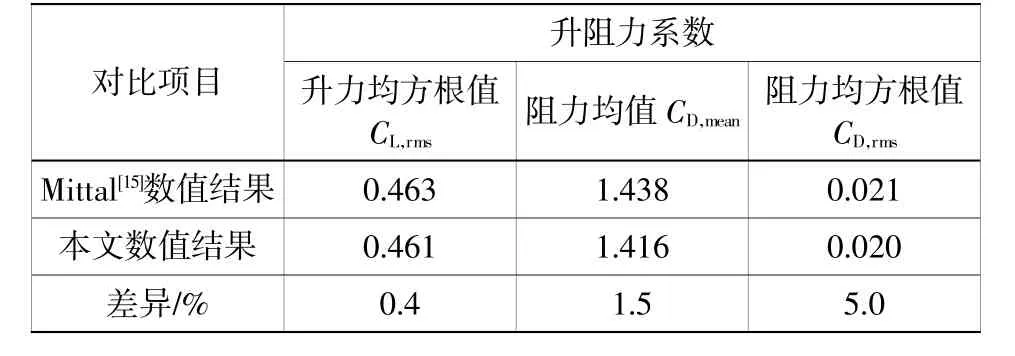
表1 主圆柱的升阻力系数对比Table 1 Comparison of lift and drag coefficients of the main cylinder

4 结果与讨论

数值模拟中，保持直径比（d/D=0.125）、间隙比（g/D=0.125）和折合流速（Ur=U∞/fnD=6）不变，通过改变俘能阻尼比ζharness、附加圆柱的方位角θ和无量纲转速α，共开展432组工况的数值模拟（见表2），系统分析各参量对系统水动力性能的影响。

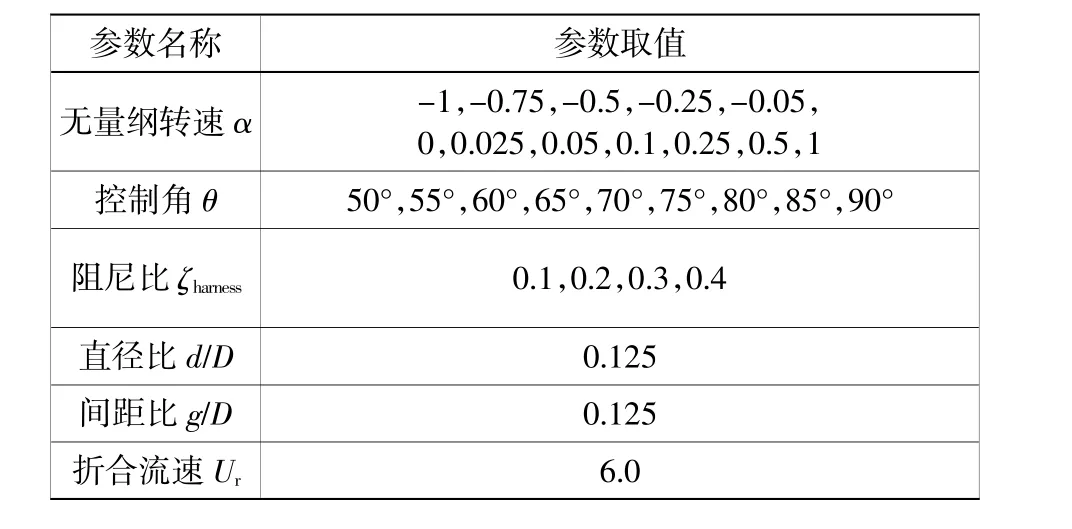
表2 数值模拟参数取值Table 2 Values of numerical simulation parameters

4.1 升力系数

图3 给出了不同俘能阻尼比ζharness条件下，升力均方根值CL，rms在α-θ参数空间内的分布。总的来看，随着无量纲转速α的增大和方位角θ的减小，CL，rms呈现增大的趋势。并且随着ζharness的增加，CL，rms较大的区域不断缩小，等值线变稀疏，说明ζharness越大，α和θ对于CL，rms的影响则略有减弱。此外，CL，rms较大的区域均出现在α＞0的情况下，说明在附加圆柱内向转动的模式下，振动系统受到的升力较外向转动的更大。这与内向转动的模式下流动更容易在控制圆柱表面发生流动分离有关，即：离开附加圆柱的自由剪切层卷起形成的漩涡经过主圆柱的侧面，导致主圆柱受到的升力增大。而在外向转动的模式下，从附加圆柱上分离的剪切层重新附着在主圆柱的表面，并在主圆柱的背流侧发生二次流动分离，导致主圆柱受到的升力较小。另外，内向转动的附加圆柱表面的线速度与来流速度方向相反，流动剪切率较大，生成的漩涡涡量较强，导致主圆柱的升力增大。

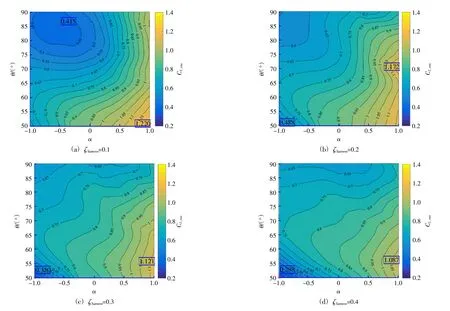
图3 升力均方根值在α-θ参数空间内的分布Fig.3 Distribution of root-mean-square lift coefficient inparameter space

图3 中方框内数字为CL，rms的最大值和最小值。随着ζharness的增加，CL，rms的最大值和最小值均不断减小。升力均方根最大值CL，rms=1.22出现在阻尼比ζharness=0.1、α=1.0和θ=50°的工况下。升力均方根最小值CL，rms=0.298出现在阻尼比ζharness=0.4、α=-1.0和θ=50°的工况下。

4.2 阻力系数

图4给出了不同俘能阻尼比ζharness条件下，阻力均值CD，mean在α-θ参数空间内的分布。整体看来，随着ζharness的增加，CD，mean呈现下降趋势，最大值阻力均值从阻尼比ζharness=0.1时的CD，mean=3.803下降到阻尼比ζharness=0.4的CD，mean=3.127。最大阻力均值出现的位置也随着ζharness的增加逐渐由参数空间的右侧中部（α=1.0，θ=70°）向参数空间的右下角（α=1.0，θ=55°）。可以看出，不同俘能阻尼比条件下，CD，mean最大值均出现在α=1.0条件下，这与附加圆柱内向转动引起的较宽的尾流有关。尾流较宽时，主圆柱的基底压强较低，导致主圆柱受到的阻力较高。

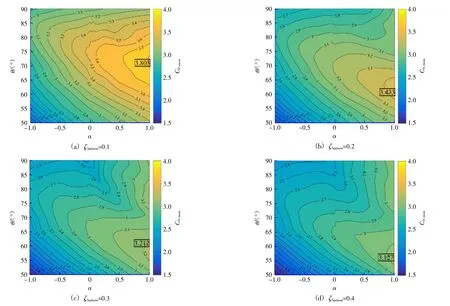
图4 阻力均值在α-θ参数空间内的分布Fig.4 Distribution of mean drag coefficient in parameter space

图5给出了不同俘能阻尼比ζharness条件下，阻力均方根CD，rms在α-θ参数空间内的分布。总的来说，随着ζharness的增加，CD，rms显著减小。ζharness=0.1时，最大均方根值CD，rms=1.044出现在（α=-1.0，θ=75°）工况下。ζharness=0.4时，最大均方根值CD，rms=0.553出现在（α=1.0，θ=85°）工况下。随着ζharness的增加，CD，rms在α-θ参数空间内的分布趋于更加均匀。这说明，高俘能阻尼比条件下，阻力均方根值受附加圆柱的转速和方位角的影响明显减弱。

图5 阻力均方根在α-θ参数空间内的分布Fig.5 Distribution of root-mean-square drag coefficient in parameter space

4.3 无量纲振幅

图6 给出了不同俘能阻尼比ζharness条件下，振幅最大值Ymax/D在α-θ参数空间内的分布。总体上，随着ζharness的增加，Ymax/D不断减小。ζharness=0.1时，振幅最大值Ymax/D=0.78出现在（α=0.25，θ=55°）工况下。ζharness=0.4时，振幅最大值Ymax/D=0.472出现在（α=1.0，θ=55°）工况下。在α-θ参数平面内，大振幅主要分布在方位角较小、旋转速度大于0的范围内。当方位角较大（θ＞70°）时，Ymax/D的等值线大致呈水平分布。这说明，方位角较大时，最大振幅受附加圆柱的转速影响较小。

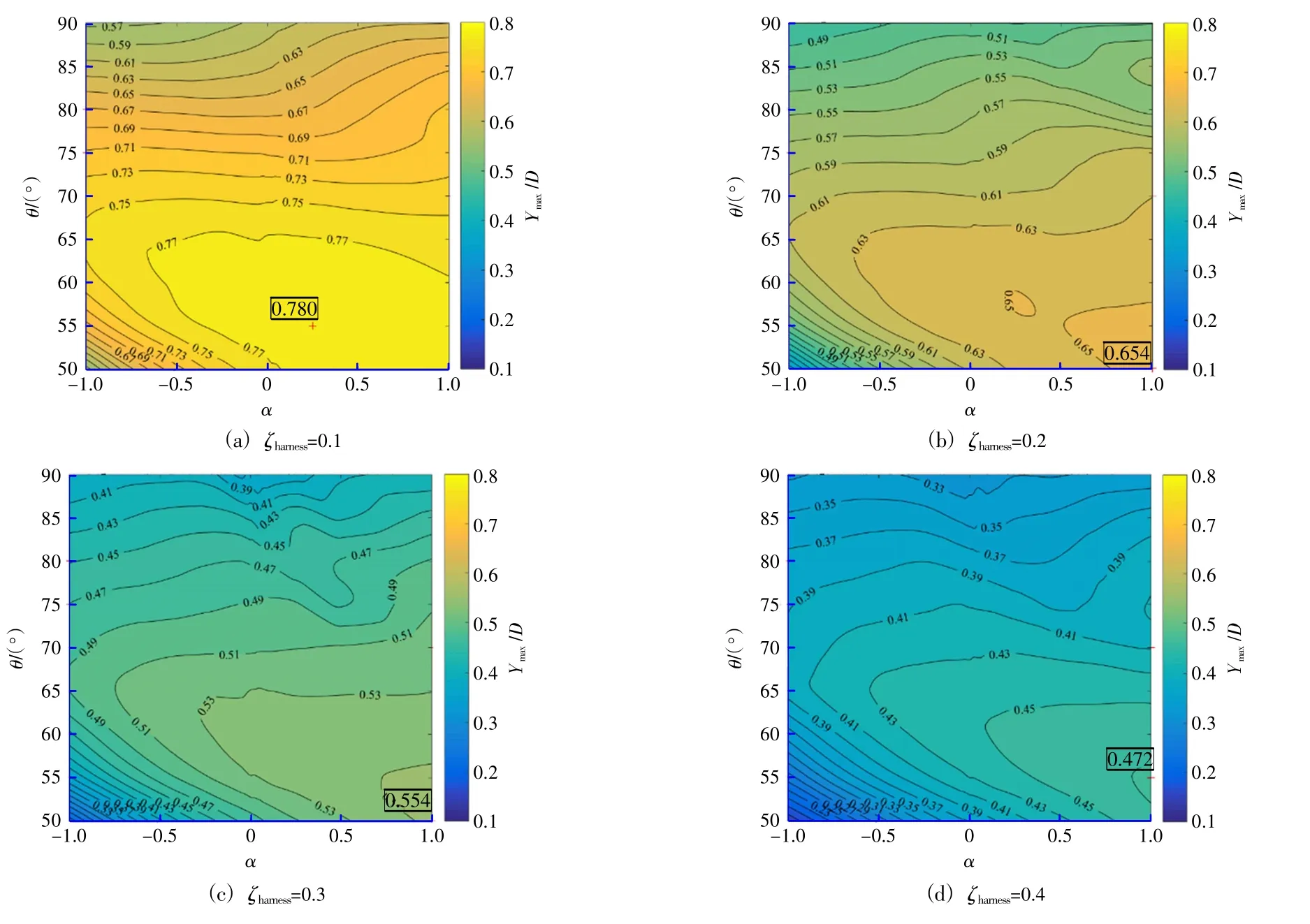
图6 无量纲振幅最大值在α-θ参数空间内的分布Fig.6 Distribution of maximum non-dimensional vibration amplitude in parameter space

4.4 组合参数（α/θ）对无量纲振幅的影响

图7 给出了无量纲振幅Ymax/D随组合参数α/θ的变化趋势。可以看出，不同俘能阻尼比ζharness条件下，Ymax/D随着α/θ的增大均呈现先增后减的变化趋势。随着ζharness的增大，Ymax/D明显降低。通过多项式拟合得到变化趋势的拟合公式为：

图7 无量纲振幅最大值随组合参数α/θ的变化Fig.7 Variation of maximum non-dimensional vibration amplitude with combined parameter α/θ

拟合公式表现为二次曲线形式。二次项系数表示曲线开口的方向和大小，即曲线变化的快慢；一次项系数表示曲线顶点位置的偏移，正值向右偏，负值向左偏；常数项表示曲线的截距。从不同ζharness条件下拟合公式系数的变化规律来看，二次项系数均为负值，随着ζharness增大而略有减小；一次项系数均为正值，说明最大的Ymax/D均在α/θ＞0（附加圆柱向内旋转）的条件下取得，这与图6中Ymax/D的变化趋势相同；常数项随ζharness增大而减小。二次项系数很小，说明拟合曲线随组合系数α/θ变化较为平缓。相反，常数项随ζharness的变化幅度较大，说明最大振幅受俘能阻尼比的影响最为显著，这与图6的结果一致。

5 结语

本文应用嵌入式迭代浸入边界法，数值模拟了主动流动控制涡激振动发电装置的水动力特性随俘能阻尼比ζharness、附加圆柱的方位角θ和无量纲转速α的变化规律，分析了升力系数均方根值CL，rms、阻力系数均值CD，mean和均方根值CD，rms、最大无量纲振幅Ymax/D在α-θ参数空间内的分布，给出了最大无量纲振幅随组合参数α/θ变化的拟合公式。具体结论如下：

1）整体来看，俘能阻尼比ζharness对于升力系数均方根值CL，rms的影响较小，而对阻力系数均值CD，mean和均方根值CD，rms及最大无量纲振幅Ymax/D则有明显的影响。

2）增大附加圆柱转速α会导致升力均方根值CL，rms、阻力均值CD，mean明显增大，而最大无量纲振幅Ymax/D变化较小；增大附加圆柱方位角，升、阻力系数和振幅均呈现先增后减的趋势。

3）最大无量纲振幅Ymax/D与组合参数α/θ呈现二次函数关系，二次项系数均为负值，随着ζharness增大而略有减小，一次项系数均为正值，随着ζharness增大而略有增加，常数项随ζharness的增大而明显减小。