基于代表性浮标观测数据的FHDI-GNWM模型主要指标精度验证
任赵飞,李伟仪,王科华
(中交第四航务工程勘察设计院有限公司,广东 广州 510230)
0 引言
目前,国际上广泛使用的全球波浪数学模型有美国NOAA的WAVEWATCH III风浪模型、美国Oceanweather Inc.的全球再分析海浪模型GROW(Global Reanalysis of Ocean Waves)、英国BMT ARGOSS的海洋气象模拟和数据服务(Met-ocean Modelling and Data Services)、欧洲ECMWF的 波浪模拟项目WAM(Wave Modelling Project)及丹麦DHI的全球波浪模型GWM(Global Wave Model),其中仅NOAA及ECMWF的波浪数据公开,其它波浪模型的后报波浪数据均未公开,需要购买,且价格昂贵。对于公开的数据库NOAA及ECMWF只能在公开网站上下载波高、周期、波向等基于全谱的波浪参数[1],不能下载波浪谱数据。而对于港内泊稳及船舶在波浪作用下的动力响应类研究,必须准确研究波浪的能量分布特征[2-4],这就需要当地波浪能量分布的波浪谱。与此同时,波浪谱对港口平面布置,尤其是防波堤掩护方向具有极其重要的指导意义[5]。
2018年底,中交第四航务工程勘察设计院有限公司(FHDI)联合交通运输部天津水运工程科学研究院(TIWTE)共同开展全球波浪研究,FHDI负责全球平常浪计算(简称FHDI-GNWM),TIWTE负责全球台风浪的计算。FHDI-GNWM将实现为用户提供全球范围内任意开阔海域、1979年至今、1 h间隔、连续的长系列波浪特征参数数据及波浪谱数据,并且高精度波浪数据的覆盖范围可从深海一直延伸至近岸-30~-50 m的等深线附近。
目前,FHDI-GNWM已完成2013年全年的波浪计算。为验证FHDI-GNWM波浪后报数据的准确性,本文选取全球23个代表性波浪浮标数据进行验证,并与其它国际已有的全球波浪数学模型的精度验证指标进行横向对比分析。
1 FHDI-GNWM简介
1.1 海浪模型
20世纪末,英国、法国、德国、挪威、荷兰等国家的海洋专家成立了WAM小组,开始第三代海浪模式的研究,其目的在于开发一个适用于全球且全面考虑各物理过程的海浪数值模式。基于当时最新研究成果,采用能量平衡方程作为控制方程,建立起以WAM模型[6]为代表的第三代波浪模型,其它的第三代模型还有Tolman提出的WAVEWATCH模型[7]以及荷兰代尔夫特大学开发的SWAN模型[8]等。
当前,在国际知名度较高的全球波浪数学模型中,美国NOAA和英国BMT全球波浪数值模型均基于WAVEWATCH III模型,欧洲ECMWF全球波浪数值模型基于WAM模型,丹麦的DHI全球波浪数学模型基于MIKE 21 SW模型。
由丹麦DHI研发的MIKE 21 SW,广泛应用于远海及近岸大、中尺度的波浪预报、后报数值模拟工作[9-10]。FHDI-GNWM也采用第三代海浪模式MIKE 21 SW进行全球波浪的后报数值计算。
1.2 模型设置
FHDI-GNWM采用C-MAP、ETOP及部分工程实测地形数据作为水深数据,以全球风场数据CFSR风场作为驱动力。模型计算考虑的物理现象包括[11]:1)风生波;2)四阶波—波非线性作用;3)白浪损耗;4)底摩阻损耗;5)水深引起的波浪破碎损耗;6)水深变化引起的折射、浅水变形和部分绕射;7)冰层覆盖对模型计算的影响。
FHDI-GNWM计算 域 范围 包 括:180°W—180°E、77.5°N—77.5°S。由于南、北两极附近常年被冰层覆盖,综合考虑模型计算稳定性要求及模型计算工作量限制,77.5°N—90°N及77.5°S—90°S区不纳入全球平常浪数学模型计算域范围,但计算域内考虑冰层覆盖的影响。
模型计算采用非结构三角网格,网格大小(等效矩形网格尺度)由外海到近岸从0.5°×0.5 °过渡至0.25°×0.25°再过渡至0.125°×0.125°最终至5 km×5 km。模型计算域网格总数200余万个,包含1235个尺度在5 km×5 km以上的岛屿及岛礁。
1.3 主要验证指标
参考国际知名的全球波浪数学模型的验证参数[12-16],设定FHDI-GNWM模型验证指标(表1),要求主要验证点位置计算的有效波高Hm0与实测值(浮标)样本之间的精度检验须满足表1指标。

表1 FHDI-GNWM主要验证指标Table 1 Main verification indicators in FHDI-GNWM
对于波周期及波向,通过时间序列过程线、散点图、Q-Q图、波玫瑰图对比等方式来定性判断模拟数据的准确性。
下面以FHDI-GNWM 2013年完整1 a全球波浪模型计算进行浮标实测数据验证。
2 代表性浮标选取
基于全球开放的波浪浮标观测数据,选取数据相对完整、数据时间段涵盖2013年的23个波浪浮标观测站的观测数据作为本次浮标验证的基础,浮标详细参数见表2。

表2 代表性波浪浮标详细信息(23个)Table 2 Detailed information of representative wave buoys(23)
3 验证结果与分析
23个浮标观测站数据验证结果见表3。以浮标Australia-4进一步说明部分验证过程,见图1,其他大量图表不再赘述。

表3 23个典型波浪浮标观测数据验证结果Table 3 Validation results of observation data of 23 representative wave buoys
波高验证方面,23个代表性浮标和FHDIGNWM的波高相关系数CC除浮标Australia-1和Australia-3为0.77外,其他浮标和FHDI-GNWM计算波高相关系数均大于0.8,波高相对偏差均小于10%,样本离散度SI均小于0.3,总体满足预设验证指标。同时,从图1(a)、(c)、(d)看出,波高Q-Q图散点高度集中或对称于45°线两侧,波高玫瑰图分布特征也高度一致。总体而言,GWMN波高模拟精度满足浮标实测数据验证精度指标。
波周期验证方面,浮标和FHDI-GNWM的波周期相关系数相对较差,相关系数CC集中在0.4~0.7之间,Tp绝对值偏差在0~2 s之间,样本离散度整体小于0.3。通过对比Hs-Tp散点图图1(b)和Tp玫瑰图图1(e)、图1(f),两者波周期分布特征高度相似。参考国际知名的其他全球波浪模型验证精度,周期的相关系数同样比较低,同样采用相关系数结合Hs-Tp散点图和波周期玫瑰图等进行总体分布评价。

图1 Australia-4浮标与FHDI-GNWM计算结果对比Fig.1 Results comparison between Australia-4 wave buoy and FHDI-GNWM
4 与国际知名的全球波浪模型的验证指标对比
4.1 浮标验证数据收集
由于国外全球波浪模型的原始计算数据难以获得,故采用相同浮标进行不同数学模型验证的对比不具备可行性。本文基于公开文献资料,论述和对比不同数学模型的浮标验证结果。国际知名全球波浪模型浮标验证结果的数据来源汇总见表4。

表4 全球主要波浪模型浮标验证数据源Table 4 Source of validation data of wave buoys used by major global wave models
4.2 主要验证指标对比
本文将FHDI-GNWM精度验证指标情况与其他波浪数学模型全球范围总的精度检验指标进行对比,结果见表5和表6。特别说明,本文主要论述波浪浮标观测数据的验证,卫星高度计波浪数据的验证工作已完成,将另行论述。
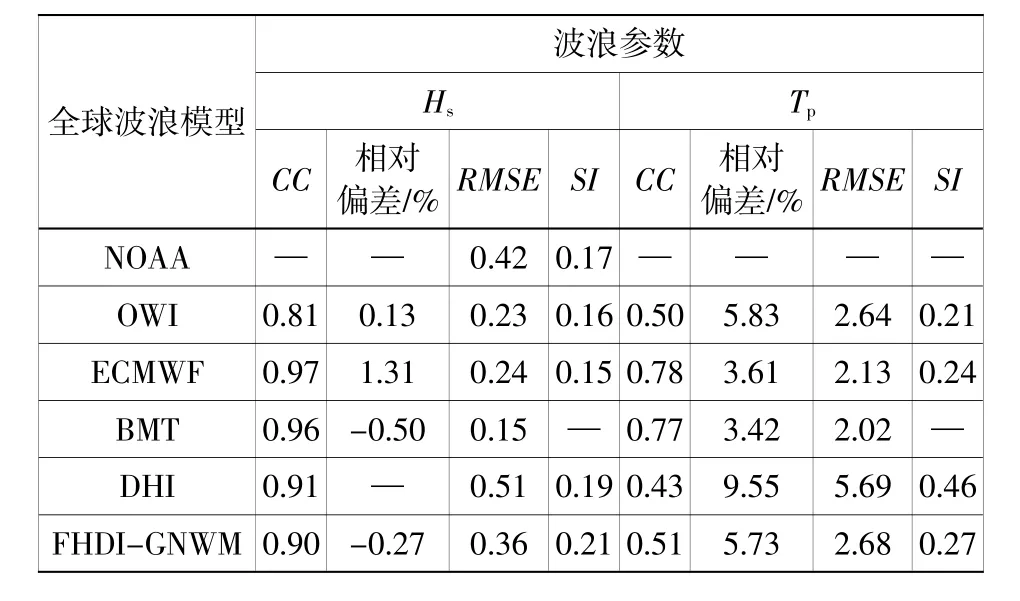
表5 FHDI-GNWM与其他全球波浪数学模型基于波浪浮标观测数据的精度检验指标参数的对比Table 5 Comparison of accuracy test indicators of FHDI-GNWM with that of other global wave mathematical models based on observation data from wave buoys

表6 FHDI-GNWM与DHI全球波浪数学模型精度检验指标分布情况(Hs和Tp)对比Table 6 Comparison of accuracy test index distribution(Hs&Tp)of FHDI-GNWM with DHI global wave mathematical model
从表5和表6可以看出,不同的全球波浪数学模型在波高的验证环节均比较良好,相关系数CC均在0.9左右(除OWI浮标验证的相关系数CC=0.81,相对较小),总体相对偏差可控制在2%以内,总体离散度SI在0.2以内(GNWM的总体离散度SI=0.21,相对较大);在周期验证环节,GNWM的验证参数略优于DHI模型,但均存在相关系数较低、相对偏差较大以及离散度较大的现象,周期验证需要结合Hs-Tp联合散点图、波周期玫瑰图/频率分布图等进行总体分布特征评价。
5 结语
本文通过选取全球代表性波浪浮标数据验证FHDI全球平常浪数学模型计算结果的精度,结果表明:模型计算波高与浮标实测波高的验证结果较好,满足预设目标;模型计算周期与浮标实测周期的相关系数普遍较低,但是分布特征高度一致。横向与国际知名的波浪数学模型基于浮标实测数据的精度验证指标进行对比,结果表明:不同的全球波浪数学模型在波高的验证环节均比较良好,但在周期验证环节,均存在相关系数较低、相对偏差较大以及离散度较大的现象,周期验证需要结合Hs-Tp联合散点图、波周期玫瑰图/频率分布图等进行总体分布特征评价。选用FHDIGNWM等数学波浪模型进行重现期波浪分析时,波浪周期取值应结合Hs-Tp联合分布图等以置信区间的形式提供,最大限度降低单一波周期绝对偏差较大可能引起的设计风险。

