基于Abaqus的SAE分体法兰密封影响因素仿真分析

何川，白本奇，叶成，何磊

(中国空气动力研究与发展中心，四川绵阳 621000)

0 前言

目前，风洞现场中快速阀、调压阀以及喷管成型动作均采用液压油缸作为执行机构，液压系统是风洞运行的主要动力源。硬质不锈钢油管亦被广泛选作为连接油源、控制阀组的重要管路，其中油管中工作压力通常都不低于20 MPa。油管在长期高压、振动的工况下，管路泄漏已经成为风洞液压油源系统最主要的故障之一。液压系统一旦故障就会造成风洞运行停摆，直接影响风洞运行的可靠性和安全性，严重降低型号试验的效率[1]。目前为止，针对液压管路泄漏问题，国内外学者对液压系统管路连接以及法兰连接的泄漏问题展开了广泛研究。程改霞和姜晋庆[2]通过分析管接头在小弹性变形条件下的力学模型，得到管接头载荷与密封面上应力分布的规律。王振兴等[3]利用有限元法定量分析了管路连接副在拉伸载荷下的密封性能。丁建春等[4]利用有限元分析软件Abaqus静力分析了管接头在拧紧力矩下的密封带宽，并建立了管接头拧紧力矩与密封带宽之间的关系。邹明德等[5]分析得到油管连接法兰O形密封圈泄漏失效是预压缩量不足，通过ANSYS建立有限元模型得出O形密封圈的最佳压缩率范围。吴林涛等[6]通过研究大直径法兰泄漏得到法兰密封泄漏仅由法兰偏转和密封面不平整问题引起。纪军[7]采用有限元法分析得出影响O形密封圈静密封性能的决定因素是预压缩量。风洞液压系统硬质管路的连接多普遍使用不同直径的高压分体式法兰，根据现场应用情况来看，管路泄漏点多出现在法兰连接处，当敷设在地坑中的油管发生泄漏时，不易及时发现，致使油箱液位下降，影响液压系统正常工作。此外地坑下管道布置在有限空间内，维修操作也十分不便，因此对液压系统中硬质管路连接的密封性研究具有重要意义。

针对液压管路密封的研究中鲜有研究高压法兰密封失效的现状，本文作者从风洞现场液压油管泄漏实际情况入手，在现场处理管道渗漏点的过程中发现渗漏主要由三类原因引起：(1)法兰夹的连接螺栓松动；(2)密封圈破损或者断裂；(3)密封圈没有损坏，螺栓连接也未松动，却出现油液缓慢渗漏的现象。针对第三类泄漏问题，拆装维修过程中发现松开法兰连接螺栓后，被释放的两根油管存在较大的径向偏差和角度偏差，回装过程中的管道同轴装配的阻力很大，判断为配管和焊接处理引起位置偏差影响了管道密封性能，如图1所示。

图1 试验现场密封失效原因

本文作者选取试验现场液压系统中使用频率较高的分体式连接法兰为研究对象，基于有限元分析法，在Abaqus软件中建立SAE分体法兰的连接模型。根据分体式法兰的密封原理分析连接法兰密封性的影响因素，通过静力学仿真计算定量分析密封参数在各影响因素下的变化规律，为现场液压管路的焊接布管和安装偏差控制提供一定的理论参考。

1 SAE分体式高压法兰结构简述

文中选取的分析对象为公称通径为25 mm的SAE分体式法兰，如图2所示,其尺寸可通过JB-ZQ4187—97查得。

图2 B型SAE分体式高压法兰实物

B型分体法兰主要由一个整体法兰夹、两个半体法兰夹、带密封槽焊接头、无密封槽焊接头、螺栓、垫圈、螺母以及O形密封圈组成，其三维组件模型如图3所示。

图3 分体法兰组件模型

在法兰连接油管的过程中，螺栓的预紧力通过法兰夹传递到焊接管接头，使密封圈轴向压紧在两个焊接头端面之间，形成密封面。

2 SAE分体式高压法兰有限元模型

2.1 分体法兰组件材料的本构模型

文中研究的SAE B型高压分体式对开法兰接管材料为304不锈钢，其力学性能[8-9]参数如表1所示。

表1 304不锈钢的力学性能参数

O形密封圈材料为丁腈橡胶,属于超弹性体，具有高度非线性行为。对于这类非线性问题，伍开松等[10]对合理选择橡胶材料的本构模型进行了总结归纳，有限元分析中较多采用Mooney-Rivlin模型来描述其力学行为；王智宇和王安稳[11]采用多元线性回归法确定橡胶Mooney-Rivlin模型常数;胡琦[12]在不同温度下对丁腈橡胶进行单轴拉伸和平面剪切试验,获得工程应力应变数据并通过线性回归曲线拟合得到Mooney-Rivlin常数，其中C1=1.946 1、C2=0.461 9。另外，橡胶是一种体积近似不可压缩的材料，其泊松比μ接近于液体的泊松比0.5，通常在0.45～0.499 9内变化。

2.2 分体法兰泄漏分析的有限元模型

分体法兰连接处渗油的根本原因是密封面密封能力不足，文中主要建立两组有限元模型来研究分体法兰密封性能的影响因素及变化规律:(1)以密封圈为研究对象，将带密封槽接管与不带密封槽接管视为刚性体法兰分别进行分析，研究密封圈预压缩率以及工作油压对密封性能的影响[13];(2)以两个焊接头和O形密封圈为主要研究对象，建立简化的三维有限元模型，分别计算两根对接油管的径向偏差、角度偏差对法兰连接密封性能的影响[14]。

2.2.1 密封圈分析有限元模型

橡胶密封圈安装于密封槽内，在螺栓预紧力下压紧无密封槽接管的端面形成密封。分析密封圈的预压缩率与工作油压作用时不考虑装配偏差，则满足几何对称、边界条件对称、载荷对称，因此可以将密封圈受压模型简化为二维模型。丁腈橡胶材料的弹性模量为7.8 MPa，而用作焊接头的不锈钢材料的弹性模量为190 GPa，两者相差近10万倍，建模过程中可以将管接头视为刚体。在接触对设置中将密封圈与密封沟槽以及焊接头端面接触设置为通用接触对，从面为密封圈外边缘，主面为密封沟槽以及焊接头端面；在边界条件中，设置带密封沟槽一侧焊接头固定，焊接头端面给定轴向位移模拟焊接头轴向压紧密封圈；在密封圈上边缘施加压力模拟液压油的工作压力。O形密封圈的二维有限元模型如图4所示。

图4 O形密封圈二维有限元模型

2.2.2 焊接头装配偏差分析有限元模型

在现场管道布置安装过程中，油管安装位置偏差难以避免，被连接的两根油管存在不同程度的径向偏差和角度偏差，从而影响连接法兰密封性能。此次分析主要关注焊接头对接端面以及密封圈上的参数，因此在建立装配偏差分析的模型时简化部分小特征，同时为保持密封部位的分析精度，对密封沟槽底的过渡圆角进行网格加密，其中无密封槽焊接头、密封圈、带密封槽焊接头的网格数量分别为5 015、15 564、5 432个，有限元模型如图5所示。

图5 装配偏差分析有限元模型

根据《机械设计手册》[15]所提供的螺栓连接预紧力控制方法，螺纹连接推荐用预紧力限值如下：

F=(0.6～0.7)σsAs

(1)

式中：σs为螺栓材料屈服强度，MPa；As为螺栓的公称应力截面积，mm2。

(2)

式中：d2为外螺栓的中径，mm；d3为螺栓的计直径，d3=d1-H/6,d1为外螺栓的小径，mm；H为螺纹原始三角形高度，mm。

查机械设计手册，得到文中分析的分体式法兰连接螺栓的中径为10.863 mm、小径为10.106 mm、螺纹原始三角形高度为1.515 mm，代入公式(1)(2)得到单根螺栓的预紧力为12 387 N。结合文中分体式法兰连接的焊接头结构尺寸与受力形式，计算得到4颗螺栓作用在焊接头承载面的压力为55.2 MPa，可以将它作为有限元分析的已知预紧载荷。

3 仿真结果与分析

3.1 O形密封圈预压缩率分析

通过4组不同预压缩率(ε=12%、ε=15%、ε=20%、ε=24%)有限元模型，模拟密封圈在20 MPa油压作用下的受力情况。密封圈在同一工作油压、不同预压缩率下的应力云图如图6所示。可以看出：Von Mises应力峰值基本随着预压缩率的增大略有增加，O形圈横截面应力分布随着预压缩率增大而逐渐趋于均匀。

图6 不同预压缩率下等效应力云图

分体法兰连接的密封性能主要取决于密封带宽度与接触应力情况。密封带指的是无密封槽焊接头端面与密封圈的接触面，如图7所示。

图7 O形密封圈密封带示意

密封圈在不同预压缩率ε下接触应力沿着密封带宽度方向的分布情况如图8所示。可以看出：密封圈最大接触应力随着预压缩率的增大而增大；当预压缩率低于15%时，密封带上最大接触应力低于工作油压20 MPa，不满足密封条件。

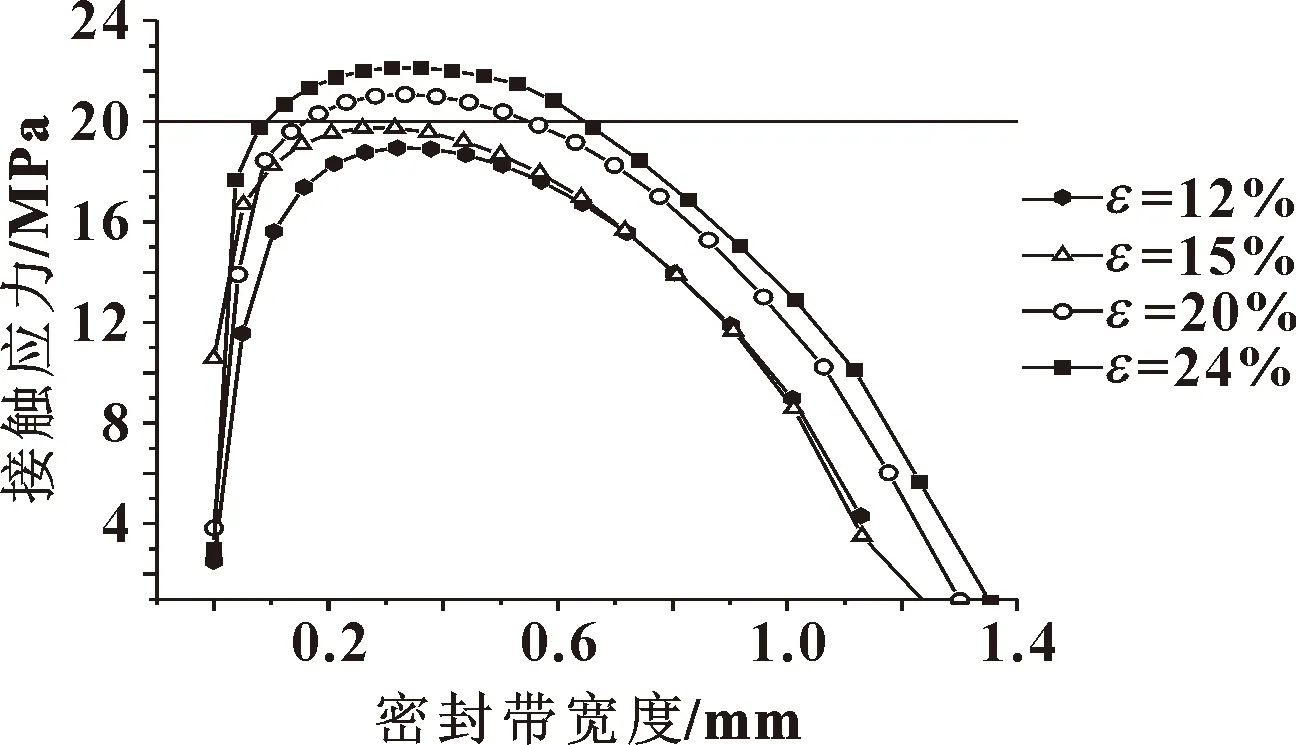
图8 接触应力分布规律

3.2 不同油压下密封性能分析

在预压缩率ε=24%时，建立9组不同工作油压(1、2、3、4、5、10、15、20、25 MPa)的数值模型，分析油源启动至压力升至目标压力的过程中，密封圈上等效应力与密封带上接触应力的变化规律，如图9所示。可以看出：油压升高，密封圈的最大等效应力增大，密封带上最大接触应力也随之增大，并且最大接触应力始终大于工作油压，体现了O形密封圈的自密封性质。另外，从接触应力随工作油压变化的规律中还可以看出：当工作油压大于5 MPa时，最大接触应力与工作油压之间表现出同步跟随性，即最大接触应力与工作油压保持相同的数值增量同步增大。

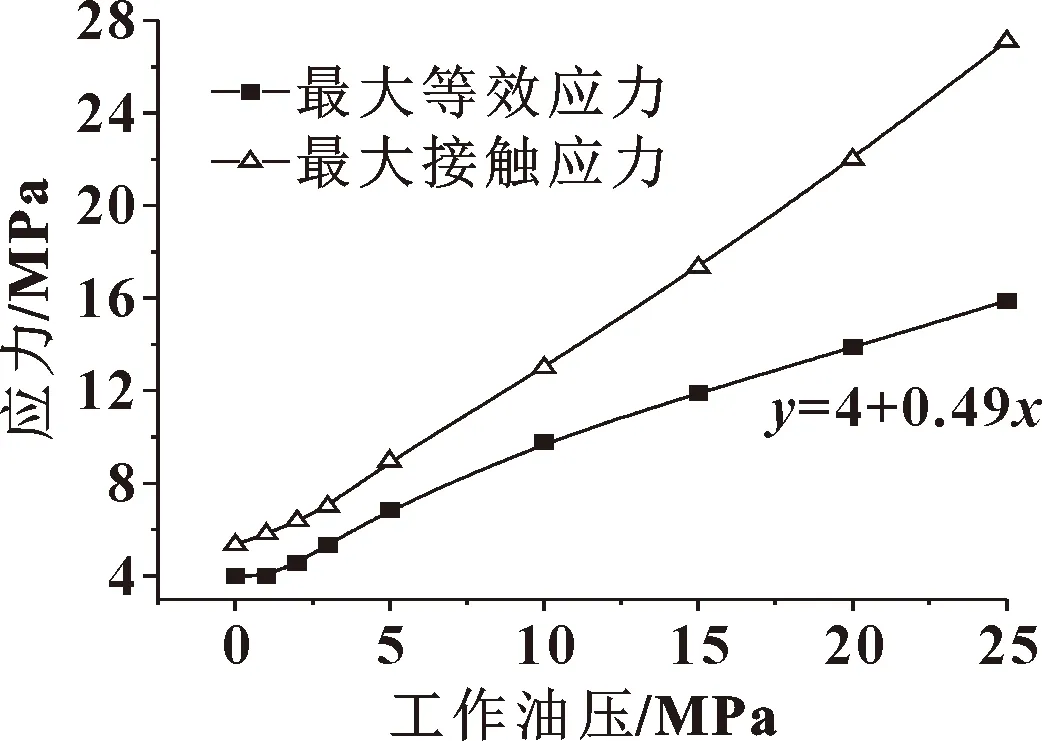
图9 密封圈应力值随工作油压变化规律

3.3 油管径向偏差对密封性能的影响

有限元模型中，无密封槽一端为固定约束，对带密封槽焊接端面所有节点施加强制位移，模拟安装过程中存在的径向偏差。设置径向偏差取值为0.1～0.5 mm，步长为0.1 mm，共5组计算模型。从计算结果中得到：随着分体式法兰的焊接头径向偏差增大，焊接头材料内部的Von Mises应力增大，且焊接头两对接端面接触应力出现一侧增大、一侧减小的趋势，如图10所示。当径向偏差达到0.4 mm时，焊接头对接端面局部区域接触应力为0，说明对接端面出现了局部分离情况，即密封圈局部预压缩率开始降低，出现局部预压缩率不足现象，密封性能降低，发生泄漏的概率增大。

图10 焊接头对接端面接触应力云图

另外，分析5组径向偏差模型的结果，发现密封带上的接触应力分布情况一致，应力都是由密封带中间位置向两侧逐渐降低。径向偏差为0.5 mm时，密封圈接触应力分布云图如图11所示。

图11 密封圈接触应力分布云图

接触应力沿密封带的分布规律如图12所示。可知：只要径向偏差不足以使对接端面脱离，O形圈在预压缩状态仍可以在20 MPa的工作油压下实现有效密封。当径向偏差大于0.5 mm时，接触端面放松一侧的密封圈上的接触应力逐渐变小，密封圈有效密封宽度变窄，失去了密封能力。

图12 接触应力沿密封带的分布规律

3.4 油管径向偏差对密封性能的影响

角度偏差是指两根被接油管轴线的相对角度，当与焊接头连接的两根油管轴线共线时，表示角度偏差为0°。通过建立5组不同的角度偏差计算模型，研究角度偏差对橡胶圈密封性能的影响。有限元模型如图13所示。

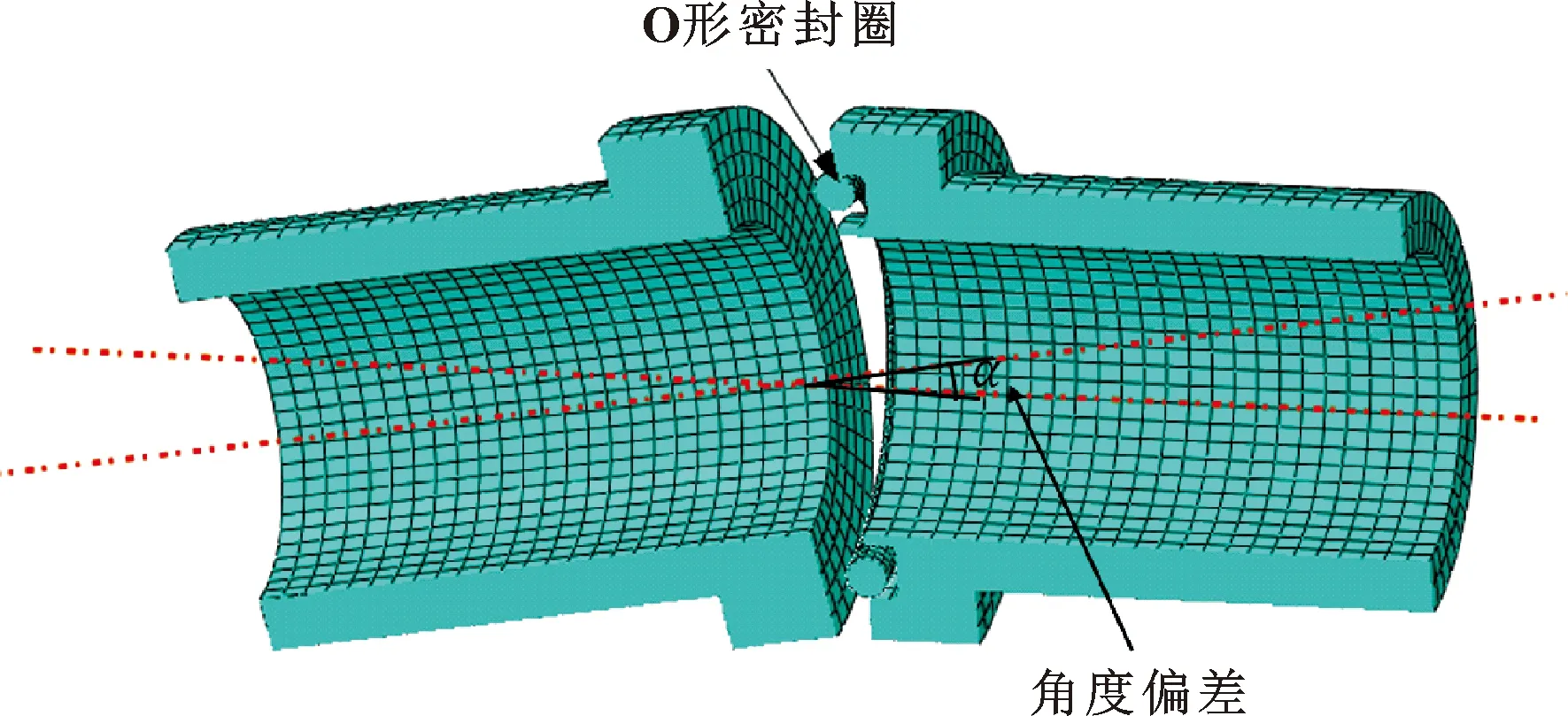
图13 角度偏差分析有限元模型

模拟计算螺栓预紧后对接端面接触应力分布情况与焊接管头材料内的等效应力，如图14—图15所示。可以看出：焊接管接头在用分体式法兰连接预紧之前存在的中轴线角度偏差值越大，焊接头对接端面上等效应力与接触应力分布不均匀程度越明显；当焊接头角度偏差为5°时，最大等效应力为223.4 MPa，即焊接头接触面出现局部材料屈服。

随着角度增大，对接面上接触应力不均匀程度增大，局部最大接触应力明显增大；但是在端面压力和油压的作用下，密封圈上沿着径向的接触应力情况不受角度偏差的影响，如图16所示。

图14 焊接头不同角度偏差预紧后接触应力分布云图

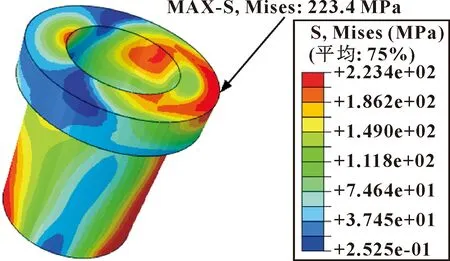
图15 焊接头偏差5°时材料内等效应力

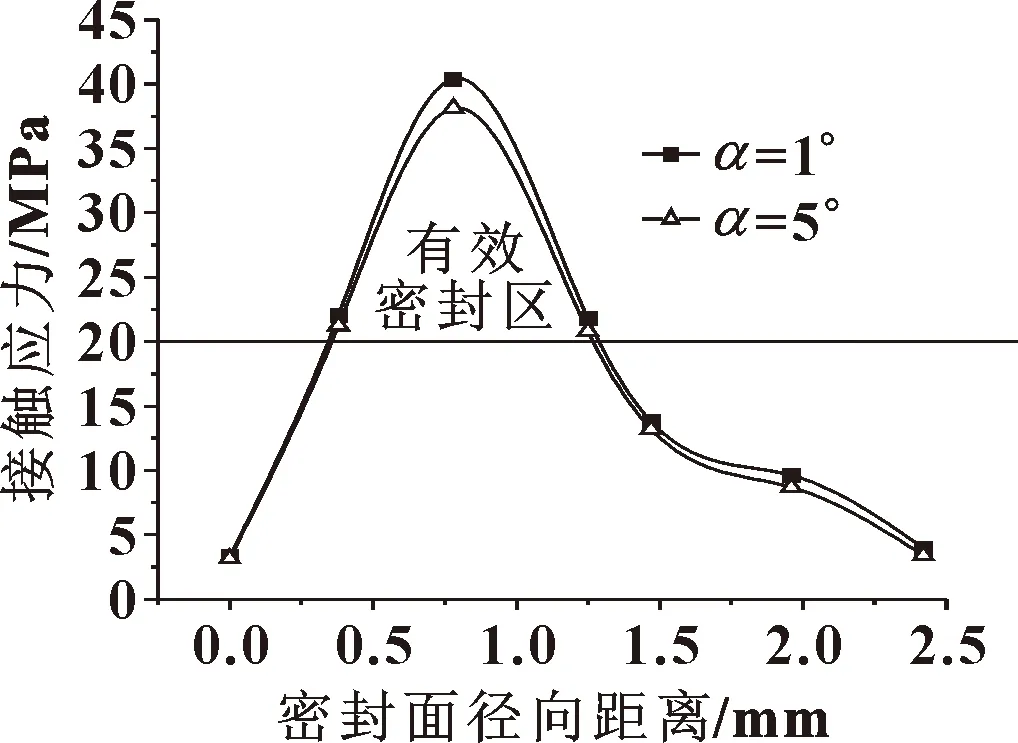
图16 角度偏差对密封接触应力的影响

4 结论

本文作者对风洞试验现场液压油管连接用得最为广泛的分体式高压法兰进行密封性有限元分析，得到如下结论：

(1)不考虑油管连接装配偏差，O形密封圈在12%～24%的预压缩率下，随着压缩率增大，主密封面上接触应力增大；在20 MPa油压的作用下，密封圈横截面内的 Von Mises应力分布越均匀，但最大等效应力与预压缩率无关；

(2)在相同的预压缩率下，工作油压增大，密封圈内最大等效应力与接触应力随之增大，并且当工作油压大于5 MPa时，接触应力跟随工作油压同步增大；

(3)径向偏差与角度偏差增大时，法兰焊接头对接端面一侧压紧，对侧放松；压紧一侧接触应力与Mises应力增大，对侧相应的值减小；偏差越大，分布不均匀程度越大，但密封圈主密封面上的接触应力不变；当径向偏差大于0.5 mm、角度偏差大于5°时，焊接头对接端面压紧一侧出现局部屈服，放松一侧密封圈上局部接触应力小于工作油压，密封失效。