基于WOA-SVR的电主轴热误差优化建模

问梦飞，钟建琳，彭宝营，王鹏家，王增新

(1.北京信息科技大学机电工程学院，北京 100192;2.超同步股份有限公司，北京101500)

0 前言

随着高精密自动化制造技术的迅速发展，对于数控机床的精度要求越来越高。而在机床各项误差中，由热变形导致的加工误差占比最高可以达到70%[1]。电主轴作为现代数控机床中的关键部件，由于其零传动的结构特点，热量不易散出，加剧了主轴的热变形，将直接影响产品的加工质量。因此，减小机床热误差对加工精度的影响成为国内外众多学者的研究方向。

目前降低机床热误差主要有两个着手方向[2]：(1)改善结构和装配工艺、加强散热和改善各部件温度升降不均等情况；(2)通过检测热误差，运用一定数学方法建立预测模型，并对可能产生的热误差预先加以补偿，称为热误差补偿法。热误差补偿法成本低、实用性强，是提高工件加工质量的重要方法[3-4]。如何建立精度高、泛化能力强的预测模型成为要点难题，近年来，国内外许多学者提出了很多有价值、应用性强的建模方法。邝锦祥等[5]根据误差值、工况转速和时间的某种规律，建立了自然指数函数模型，其模型简单、精度较高，但是该模型的预测精度取决于用于建模的函数，对不同情况的适应性不足。戴野等人[6]利用自适应神经模糊推理系统建立了热误差模型，该模型鲁棒性强、预测精度高，在不同转速条件下适应能力强、抗干扰能力强。鞠萍华和黄洛[7]建立了灰色GM(1,4)预测模型，预测结果与实际热误差残差在1 μm以内，但此模型对非线性数据样本预测效果差。张捷等人[8]建立了遗传RBF神经网络预测模型，遗传RBF模型的精度和鲁棒性均优于传统RBF神经网络法和多元线性回归法。LIU等[9]结合深度学习与灰狼寻优算法建立了长短时记忆神经网络模型，利用变分模态分解将非平稳的数据转化至较平稳，取得了良好的效果。TAN等[10]利用LASSO回归法筛选温度测点，建立最小二乘支持向量回归模型，结果表明此方法建立的LS-SVM模型预测性能好、泛化能力强，并且支持向量回归(Support Vector Regression，SVR)模型在小样本情况表现良好、泛化能力强，有大量的核函数可以使用，可以灵活解决回归问题。

本文作者采用模糊聚类的方法，消除温度变量间的多重共线性，利用灰色关联度分析(Grey Relation Analysis，GRA)法对各温度变量进行关联度排序，筛选出温度关键点；针对支持向量回归模型的不足，采用鲸鱼优化算法获得关键参数c和g的最优值，建立电主轴热误差预测模型。

1 电主轴温升和热误差实验系统

研究对象为数控加工中心某型号电主轴，该电主轴常用加工转速为7 000～10 000 r/min，前后轴承处为油脂润滑，外置水冷机循环冷却，实验条件为空转。

电主轴的热源主要来自于电机损耗发热和前后轴承处摩擦生热[11]。温度传感器主要布置在前后轴承室，电机温度由西门子840D系统同步采集，温度传感器型号选用PT100A，具体分布如图1、图2所示。采用电涡流位移传感器采集轴向热误差数据，放置在电主轴前端0.8 mm处，如图3所示。利用美国雄狮回转误差分析仪进行位移传感器位置的确定和校准。采用电主轴安装于机床上的方式，选取10 000 r/min转速进行实验，得到的热伸长量更接近实际加工工况。测量过程中环境温度保持在27°C左右，水冷机设置为室温同调。

图1 后轴承附近温度传感器

图2 前轴承附近温度传感器

图3 位移传感器

传感器编号及位置说明如表1所示。

表1 传感器位置说明

温度传感器T1测量电主轴后轴承室温度的变化，T2—T6测量前轴承室周围的温度变化，T7测量电机温度。

实验转速设置为10 000 r/min，运行总时长180 min，采集仪采样间隔34 s，空载运转。

实验中共采集到319组数据，各温度测点的温升曲线如图4所示。轴向伸长量如图5所示。

图4 温升曲线 图5 轴向伸长量

由图4—图5可知：在1.5 h左右，温度趋于稳定，电主轴的伸长量也趋于稳定，并且10 000 r/min转速时，前轴承处发热大于电机发热。实验测得最大轴向伸长量为79.93 μm，平均轴向伸长量为67.96 μm。

2 电主轴温度测点优化

2.1 模糊聚类

模糊C均值(Fuzzy C-means)算法简称FCM算法，在数据的聚类方面应用广泛，理论成熟。FCM算法根据欧几里得原理构建目标函数，利用拉格朗日法求目标函数的极值，推导出隶属度矩阵[uij]和聚类中心点ci的迭代公式，不断迭代直至达到终止条件，根据最终得到的隶属度矩阵，对温度测点进行分类。通过分类，可以有效地消除变量间的多重共线性。

目标函数及约束条件如式(1)[12]所示：

(1)

其中：m为模糊指数，通常取1.5～2.0；c为分类数。根据式(1)推导，uij和ci的迭代公式分别如式(2)和式(3)所示：

(2)

(3)

2.2 灰色关联度分析

采用灰色关联度分析法，分析每一组中每个温度测点与热伸长数据之间的关联度，选取关联度最大的温度测点作为关键点[13]。

算法实现步骤如下：

(1)确定分析数列。文中热伸长数据作为母序列，又称参考序列：

Y=Y(k)|k=1,2,…,n

各温度测点的测量值作为子序列，又称比较序列：

Xi=Xi(k)|k=1,2,…,m

(2)数据的均值化处理。样本数据存在量纲不同的问题，如不做处理，难以得到准确的结果，因此需对数据进行均值化处理，公式如下：

(4)

(3)采用式(5)计算关联系数[14]:

ξi(k)=

(5)

(4)最后进行关联度排序：

(6)

2.3 温度测点优化结果

经过迭代，最终得到的隶属度矩阵U为

聚类结果如表2所示。

表2 聚类结果

根据式(5)和式(6)，得到各温度测点的关联度排序结果如表3所示。

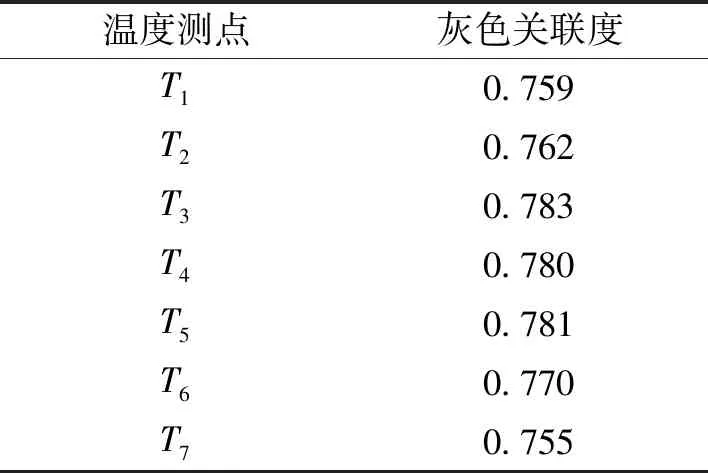
表3 各测点关联度排序

由表3可知：关联度由大到小为T3、T5、T4、T6、T2、T1、T7。结合模糊聚类的结果，可选出温度关键点为T3、T6、T7。

3 鲸鱼算法优化支持向量回归电主轴热误差建模

3.1 支持向量回归模型

支持向量回归模型应用广泛，算法的核心为构建超平面和间隔带，使超平面和最远的样本点之间的距离最小，主要原则：在间隔带内的样本点不计损失值，f(x)与y之间的绝对差值大于ε的样本点才计入损失。并且利用核函数将低维数据映射到高维，将非线性问题近似地变成线性回归问题。目标函数和约束条件如式(7)[15]所示：

(7)

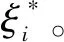
3.2 鲸鱼算法优化SVR模型

鲸鱼算法(Whale Optimization Algorithm,WOA)提出于2016年，其整个过程主要分为三部分：包围猎物、气泡网捕食、搜索猎物。通过数学模型描述座头鲸的捕猎行为，以寻找最优解。该算法具备群体智能优化算法的实现简单、稳定性好、灵活性强等优点。

群体中其他个体朝着最优位置收缩包围的过程，称为包围猎物。使用以下公式对最优位置的位置向量进行更新[16]：

D=C·X*(t)-X(t)|

(8)

X(t+1)=X*(t)-A·D

(9)

其中：t为迭代次数；A和C为系数；X*为群体最优解的位置向量；X为当前的位置向量。A和C的计算公式如下：

A=2·A·r-a

(10)

C=2·r

(11)

式中：a为收敛因子，在算法执行过程中从2衰减到0；r为[0,1]之间的随机数。

a=2-2t/tmax

(12)

座头鲸捕食时采用螺旋向上游动的路径，在游动的同时，吐出大量气泡来形成气泡网，用气泡包围猎物，此过程称为气泡网捕食。建立以下数学模型模拟此行为：

(13)

式中：D′表示个体当前位置与最优猎物的距离；b为常量；l为[-1,1]之间的随机值。为模拟该行为，收缩包围和螺旋上升两种行为的概率均设定为0.5。

当座头鲸活动范围内没有猎物时，就会扩大搜索范围，此过程称为搜索猎物，根据系数向量A来模拟搜索猎物过程。当随机值A的绝对值大于1时，表示扩大活动范围，反之，座头鲸包围收缩。该过程的数学模型如下：

D=C·Xrand-X|

(14)

X(t+1)=Xrand-A·D

(15)

支持向量回归模型不易找到最优的c和g参数，而鲸鱼算法有良好的寻优策略,算法具体的优化流程如图6所示。

初始化种群数量为30、最大迭代次数为50、b为1，选择径向基函数RBF作为核函数，将319组温升和热误差数据随机划分为229组训练集、90组测试集，预测结果及残差如图7所示，相关性如图8所示。

图6 优化算法流程

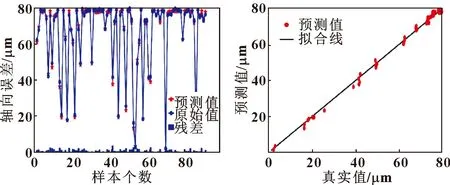
图7 优化后残差 图8 优化后相关性

3.3 模型预测效果对比

鲸鱼算法优化支持向量回归模型前后残差对比，如图9所示。优化后的支持向量回归模型WOA-SVR与多元线性回归模型MLR的残差对比如图10所示。

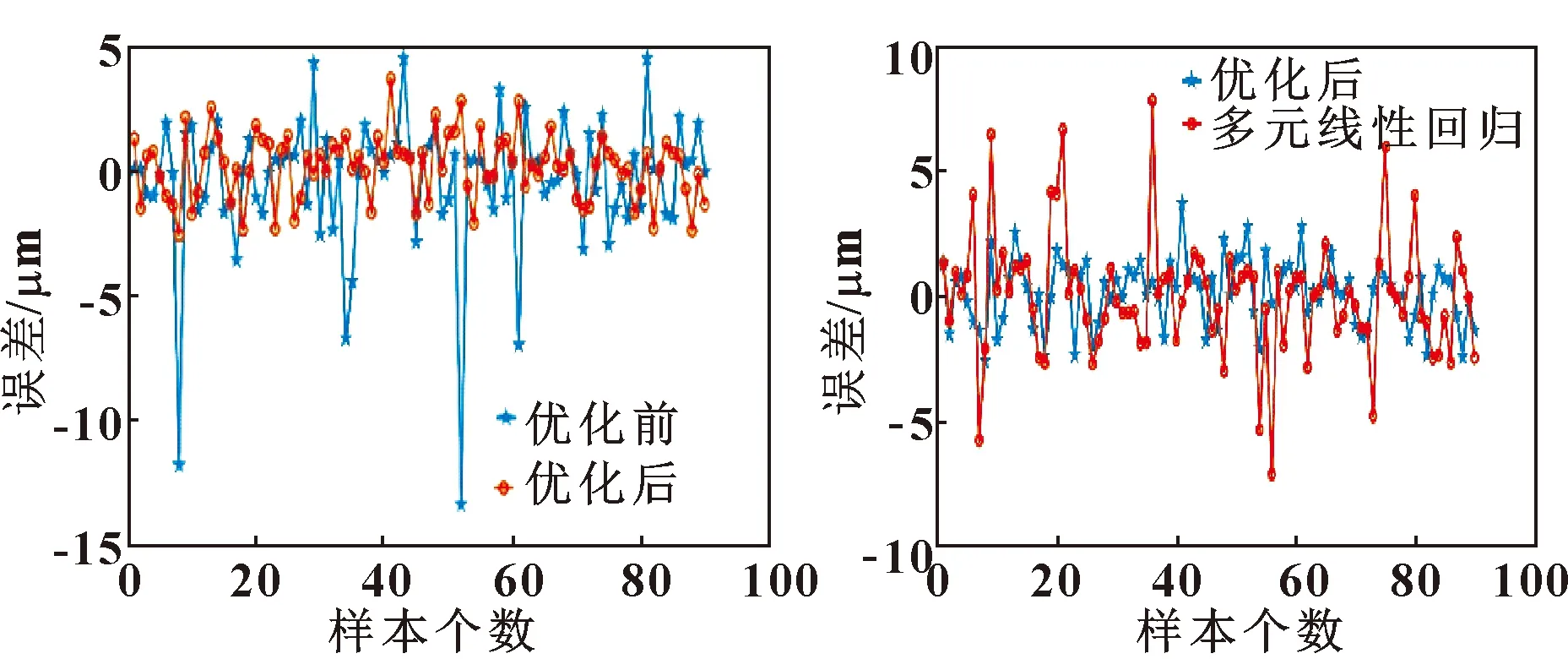
图9 优化前后对比对比多元线 图10 性回归模型

模型预测效果对比如表4所示。

表4 模型预测效果对比

4 结论

以某台电主轴为实验对象，测得10 000 r/min转速时的温升和轴向热伸长数据，建立鲸鱼算法优化的支持向量回归模型，将优化后的模型预测效果与优化前的SVR模型、多元线性回归MLR模型进行对比，得出以下结论：

(1)采用FCM-GRA结合的方法筛选温度关键点，将温度测点从7个减少到3个，避免了预测模型输入变量的冗余性和温度变量间的多重共线性，提高了建模效率；

(2)优化后的模型误差最大值和平均值均小于其他两种模型，均方根误差在1 μm左右，与未优化的SVR和多元线性回归模型相比分别减少了51%和45%，验证了WOA-SVR模型适用于电主轴的热误差预测，提供了新的建模思路。