基于FLUENT 的异径管管内流体流动特性分析

江 帆， 黄 瑞

（1. 中冶南方武汉钢铁设计研究院有限公司, 武汉 430080;2. 沈阳化工大学 机械与动力工程学院, 沈阳 110142）

0 引 言

异径管作为常用的连接管件被广泛应用于石油化工、 冶金等领域。 根据大、 小端的圆心位置， 异径管可以分为同心异径管和偏心异径管。在实际工程中， 同心异径管多应用于垂直管段，而偏心异径管多应用于水平管道， 两者均无法避免管体内发生冲蚀和腐蚀。 为了解决这一难题，工程技术人员和专家学者从不同角度对异径管进行研究， 例如应力[1-2]、 冲蚀度[3-4]、 水力损失[5]、 几何尺寸[6-7]和流体瞬态特性[8]等。 吴明亮和李永飞[1]研究了变径管壁厚、 小端角度和圆角对变径管应力的影响， 得到了最优的设计参数；陶春达等[2]以偏心异径管为研究对象， 发现通过适当增加异径管的长度来降低偏心率可以减小应力值； 何兴建等[3]首先研究了结构尺寸对异径管的冲蚀情况影响， 然后研究了在不同入口流速和入口颗粒浓度情况下异径管的冲蚀情况， 结果表明， 异径管壁面的冲蚀情况随流速和颗粒浓度的增加而严重[4]； 李凡等[5]研究了规格为DN300 mm×DN200 mm 和DN300 mm×DN250 mm×DN200 mm 的管道阻力特性， 结果表明， 相比于DN300 mm×DN250 mm×DN200 mm 连续变径管道，DN300 mm×DN200 mm 的直接变径管道阻力损失更大； 丁宇奇等[6]研究了变径比对压降的影响，结果表明， 变径比越大， 压降越小； 杨美娥等[7]研究了导热油在不同偏心比异径管内的流动特性， 结果表明， 偏心比越大， 出口最大流速越小， 管内流动的压力降越大； 索绰等[8]研究了混合油在偏心异径管内瞬时体积浓度状态。

由于不同流体具有特定的物性参数， 因此对异径管进行试验研究会耗费较多的人力和财力。相比试验研究方法， 数值模拟的方法具有费用低、速度快、 操作理想化等优点。 作为流体、 换热仿真的计算软件， CFD 被广泛应用于多个领域， 常见的CFD 软件有FLUENT、 CFX 和COMSOL 等[9-10]。本研究基于有限元分析方法， 运用FLUENT 软件， 旨在研究甲烷在同心异径管和偏心异径管中的流动特性， 得到流体在不同尺寸的异径管内压强云图和速度云图， 从而为异径管的设计、 制造和工程中防腐、 维修提供一定的理论依据。

1 建立数学模型

数学模型将甲烷在异径管的流动视为定常不可压缩流动。 湍流模型采用标准k-ε 湍流模型，控制方程如下所示[11]。

质量守恒方程（连续性方程） 为

式中： ux、 vy、 wz——x、 y、 z 方向上的速度分量。动量守恒方程（N-S 方程） 为

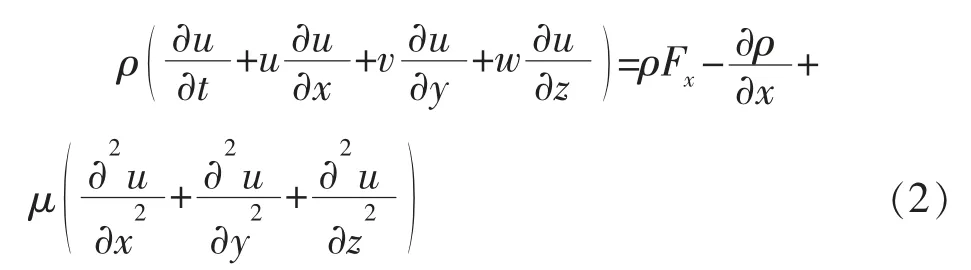
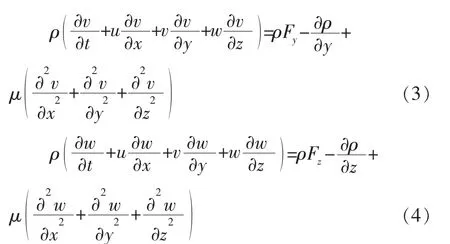
式中： ρ——流体的密度；

μ——流体的粘度系数；

Fx、 Fy、 Fz——x、 y、 z 方向上的分力。

湍动能k 及耗散率ε 方程为

式中： t——时间；

Gk——由平均速度梯度而引起的湍动能产生；

Gb——由浮力影响引起的湍动能产生；

YM——可压缩湍流脉动膨胀对总的耗散率的影响；

C1ε、 C2ε、 C3ε——经 验 常 数， 分 别 取 值 为1.44、 1.92 和0.09；

σk、 σε——湍动能和湍动耗散率对应的普朗特数；

Sk、 Sε——自定义源项；

Prt——湍动普朗特数， 取值为0.85；

β——热膨胀系数；

gi——重力加速度在i 方向的分量；

T——温度；

Mi——湍动马赫数。

2 建立有限元模型

2.1 尺寸选择

建立仿真模型时忽略管道壁厚的影响， 并在异径管的前后分别设置一段入口管和出口管。 入口管选用公称直径为DN350 mm 的管道， 长度L1为500 mm。 出口管分别选用公称直径为DN250 mm 和DN150 mm 的 管 道， 长 度L2均 为500 mm。 由GB/T 12459—2017 可得异径管的相应尺寸， 见表1[12]。

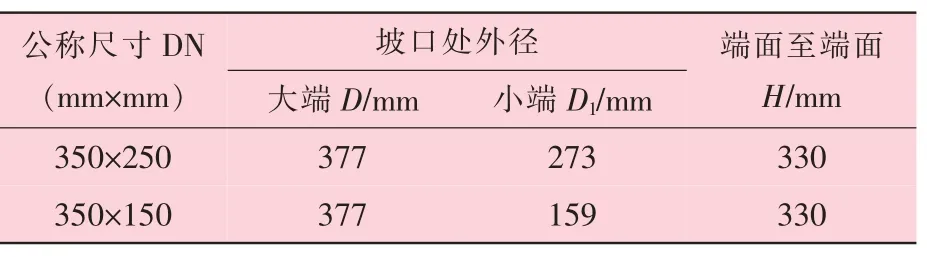
表1 异径管尺寸

2.2 建模与网格划分

同心异径管和偏心异径管的几何模型如图1所示， 其中外径D 和D1的尺寸见表1。 计算可得， DN350 mm×DN250 mm 同心异径管和偏心异径管的变径角度分别为9°和17°， DN350 mm×DN150 mm 同心异径管和偏心异径管的变径角度分别为18°和33°。 采用GAMBIT 软件分别建立同心异径管的完整模型和偏心异径管的1/2 模型， 并采用六面体网格对模型进行划分， 网格精度为0.01。

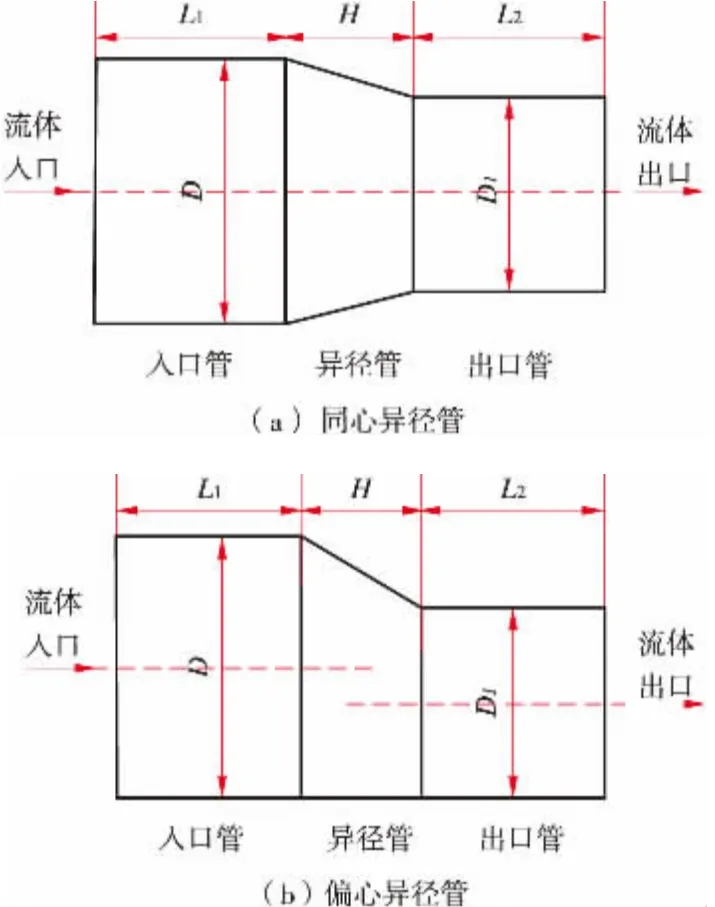
图1 异径管的几何模型

2.3 边界条件及材料物性参数

模型采用速度入口边界条件， 设定管道入口处的流体流速为5 m/s。 考虑到管道出口的压力和流速未知， 模型采用质量出口边界条件， 即为自由流出。 模型流体为甲烷 （CH4）， 壁面材料为钢， 材料物性参数见表2。

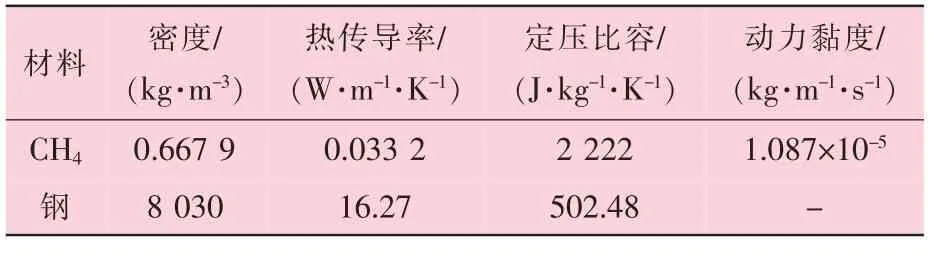
表2 材料物性参数

3 结果与讨论

3.1 压强的变化特性

图2 给出了不同尺寸的同心异径管和偏心异径管内流体的压力变化情况。 通过图2 可以看出， 当流体从大管径的管段向小管段流动时， 管道的静压呈下降的趋势。 但是在入口管与异径管的相接处存在最大压力值， 在出口管与异径管的相接处存在最小压力值， 这是由于流体在平管段流动时流态相对稳定， 当流入变径处时， 管道的截面积减小， 流体受到挤压，流速会突然增大， 流体的稳定状态被破坏， 部分静压转换为动压， 产生扰动涡旋， 因此静压值产生波动， 出现最大值或者最小值。 当同心异径管尺寸为DN350 mm×DN250 mm 时， 异径管入口处的最大静压值为1.65 Pa， 出口处的最小静压值为-11.74 Pa。 当同心异径管尺寸为DN350 mm×DN150 mm 时， 异径管入口处的最大静压值为3.20 Pa， 出口处的最小静压值为-62.38 Pa。 由上可知， 异径管的变径角度越大， 变径处形成的涡旋越强， 流体的压力损失越大。 当偏心异径管尺寸为DN350 mm×DN250 mm 时， 异径管入口处的最大静压值为3.74 Pa， 出口处的最小静压值为-19.04 Pa。由上可知， 与同心异径管相比， 相同尺寸的偏心异径管在入口处最大静压值更大， 在出口处最小静压值更小， 这主要是由于偏心异径管的变径角度增大导致。

图2 异径管管内的压强变化

3.2 速度的变化特性

图3 给出了不同尺寸的同心异径管和偏心异径管的速度场变化情况。 当入口流量一定时， 改变管道的截面积将影响流体流过截面的流速。 图3 （a）、 图3 （b）、 图3 （c）、 图3 （d）中异径管内流体的最大流速分别为7.22 m/s、8.17 m/s、 13.02 m/s 和15.55 m/s， 异径管内流体的最小流速分别为3.24 m/s、 2.56 m/s、 2.76 m/s和1.63 m/s。 由3.1 中的分析可知， 流体流经变径处流速突变， 产生扰动涡旋， 因此静压在变径管的出口处减小并转化为动压， 使得流速达到最大值， 在速度场中呈现弧线变化。 流体后续流入出口管的平管段， 逐渐恢复稳定状态。 由于变径处的流体流速大， 因此流体对变径管与平管段的接管处的冲蚀程度也变大， 此外， 在实际管道施工中， 异径管与平管段多为焊接， 不仅要考虑流体对焊接处的冲蚀， 还需考虑管道焊接的质量。因此施工时， 在变径处应采用耐腐蚀性强的钢材或增加管道的壁厚， 同时还应加强变径连接处的焊缝检测。

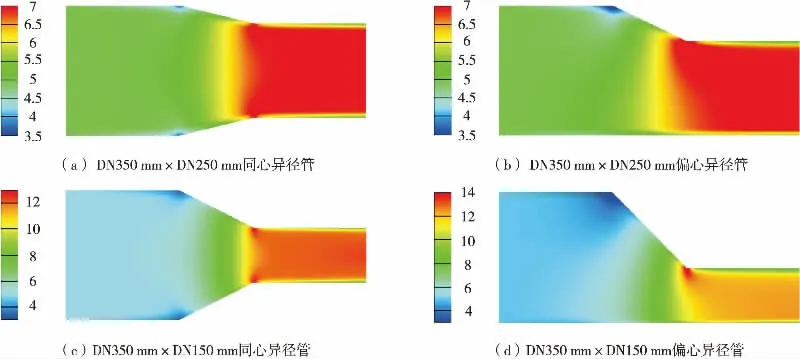
图3 异径管管内的速度场变化

4 结 论

（1） 运用FLUENT 有限元仿真软件， 对不同尺寸的同心异径管和偏心异径管进行流体流动的仿真模拟， 发现流体从平管段流经变径处时，管道的截面积减小， 流体受到挤压， 流速突然增大， 流体的稳定状态被破坏， 部分静压转换为动压， 产生扰动涡旋， 因此静压值产生波动， 出现最大值或者最小值。 异径管的变径角度越大， 变径处形成的涡旋越强， 流体的压力损失越大。 而相同尺寸的偏心异径管具有更大的变径角度， 因此相比同心异径管， 在入口处有更大的最大静压值， 在出口处有更小的最小静压值。

（2） 当流体流经变径处时， 静压在变径管的出口处减小转化为动压， 因此流速在变径处达到最大值， 继而使得变径管与平管段的接管处受冲蚀的程度也变大。

（3） 在实际管道施工中， 异径管与平管段多为焊接， 除了考虑流体对焊接处的冲蚀， 还需要考虑管道焊接的质量。 因此， 施工时在变径处应采用耐腐蚀性强的钢材或增加管道的壁厚， 同时加强变径连接处的焊缝检测。