广义带限航空矢量重力确定大地水准面的两步积分法

黄谟涛，邓凯亮，吴太旗，王伟平，欧阳永忠，陈 欣，王 许

1. 海军研究院，天津 300061； 2. 自然资源部海洋环境探测技术与应用重点实验室，广东 广州 510300； 3. 国家海洋局南海调查技术中心，广东 广州 510300

高精度高分辨率大地水准面是大地测量学科的重要科学目标之一，可为地球物理学、地球动力学、空间科学及地球资源勘探等领域提供必要的基础信息支撑，也是当前大地测量现代化基础设施建设实现GNSS测定海拔高程的重大需求[1-6]。随着高精度GNSS差分定位技术的不断发展和重力传感器制造工艺技术的不断完善，继航空重力标量测量之后，航空矢量重力测量技术也取得了重大进展[7-10]。由加拿大生产的AIRGrav重力仪获取的航空矢量重力两个水平分量的重复测量符合度已分别达到0.34 mGal(mGal=10-5m/s2)和0.28 mGal[11]，利用我国自主研制的捷联式重力仪SGA-WZ获取的航空矢量重力两个水平分量的测量精度也分别达到1.23 mGal和1.80 mGal[10]。这些结果表明，利用航空矢量重力测量水平分量观测数据确定高精度高分辨率的大地水准面已成为可能。前期国内外开展基于航空重力测量数据确定大地水准面的研究主要集中在以航空标量重力测量成果作为输入信息[3,12-15]。关于航空矢量重力测量水平分量数据的应用，文献[16—17]曾依据类似于天文水准测量的计算原理，通过采用重力水平分量沿测线剖面积分方法获得了亚分米级的大地水准面。由于该方法只能计算得到相对大地水准面高度，其推广应用范围受到了一定的限制。因此，开展基于航空矢量重力测量水平分量确定绝对大地水准面的研究具有非常现实的意义[18]。

实际上，利用航空矢量重力水平分量确定大地水准面可归结为求解一类特殊的物理大地测量边值问题，此类问题不同于传统的重力场位理论第一、第二和第三边值问题[19]。首先体现为二者的观测边界面不同，传统边值问题的边界面为大地水准面或地球表面，新边值问题的边界面则为飞行高度面，属于广义边值问题[20]；其次是二者的观测参量不同，传统边值问题的观测量一般为垂直方向上的扰动重力或重力异常，新问题的观测量则为矢量重力水平分量，属于水平边值问题[21]。因此，建立并求解以飞行高度面作为边界面的广义水平边值问题解，就成为利用航空矢量重力水平分量确定大地水准面的关键[22]。向下延拓过程是利用航空重力数据精密确定大地水准面必不可少的技术环节，由于位场向下延拓在数学上属于不适定问题，求解此类问题存在很大的不确定性[23]，国内外学者为此开展了大量卓有成效的研究工作[24-30]。文献[12—13]依据航空重力测量数据特有的带限频谱特性，推导了基于带限航空标量重力测量数据的向下延拓模型，并将其应用于大地水准面解算，仿真试验表明该方法具有良好的精度和稳定性。文献[31]全面分析比较了基于带限航空标量重力测量数据向下延拓模型与基于逆Poisson积分模型的各类正则化延拓方法的计算效果，得出的结论是前者的计算稳定性和精度都明显优于其他方法。

本文尝试将航空标量重力测量数据的带限频谱特性拓展到航空矢量重力数据处理及应用，以物理大地测量边值理论为基础，建立并求解以飞行高度面作为边界面的广义水平边值问题解，进而提出了基于带限航空矢量重力水平分量确定大地水准面的两步积分法，较好地克服了传统解算方法固有的不适定性问题。

1 计算模型

1.1 广义带限水平边值问题解

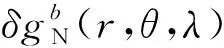
(1)

式中，r为待求或已知参数点位的地心半径；λ为点位经度；θ为点位大地余纬；R为地球平均半径。

将重力扰动位的球谐函数展开式代入式(1)的边值条件，同时顾及水平分量在球面上的正交特性，依据球函数的加法定理，可推得飞行高度面上的带限扰动位Tb(r,θ,λ)的计算公式为[18]

(2)

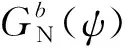
(3)

(4)

式中，Pn(cosψ)为n阶勒让德多项式；ψ代表计算点P(r,θ,λ)至积分流动点Q(R,θ′,λ′)之间的球面角距；∂Pn(cosψ)/∂cosψ代表勒让德多项式Pn(cosψ)的一阶导数；∂cosψ/∂θ′和∂cosψ/∂λ′的计算表达式为

(5)

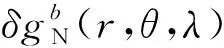
由于航空重力观测值均为离散值，故通常情况下还需要将式(2)作离散化处理。考虑到观测数据覆盖范围有限，式(2)无法进行全球积分，故在实际应用中，式(2)一般只用计算点周围有限的观测值求和来逼近所谓的近区影响，远区影响则采用国际上最新发布的超高阶全球重力位模型(UHD-GGM)进行计算。此时，式(2)将改化为

(6)

式(6)左端的第2求和项代表式(2)的积分远区影响；式(6)右端求和项代表式(2)的积分近区影响；GM为地球引力常数；Lmax为用于补偿远区效应的UHD-GGM的最高阶数。Cn(H,ψ0)为远区效应积分核函数；Tn(θ,λ)代表地球重力扰动位n阶拉普拉斯(Laplace)面球谐函数；N为近区积分半径ψ0内的测点总个数；Δσ为单位球积分面积元；其他符号意义同前。Cn(H,ψ0)的计算公式为[18]

(7)

式中，系数Rnm(ψ0)由式(8)计算[33]

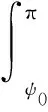
(8)

Tn(θ,λ)的计算公式为

(9)

这里需要补充说明的是，使用参考场模型GGM的目的是减弱积分远区数据影响，降低积分近区数据覆盖范围要求；使用UHD-GGM的目的则是为了补偿积分远区数据剩余影响。实践中，为了减弱高阶次位系数误差对近区积分结果的影响，一般都选择一个阶次比较适中的位模型(如360阶次)作为参考场；补偿积分远区数据剩余影响则一般采用当前国际上广泛认可的最高阶次位模型(如2160阶次)，因此，UHD-GGM的最高阶数通常都要大于GGM的最高阶数，即必须取Lmax>(l-1)。不难看出，UHD-GGM模型的实际作用是补偿积分远区数据位于GGM最高阶数至UHD-GGM最高阶数频段内的信息影响。

1.2 广义带限Dirichlet边值问题解

由广义带限水平边值问题解计算得到飞行高度面上的带限扰动位Tb(r,θ,λ)以后，还需要将空中扰动位向下解析延拓到海平面(海拔高程起算面，也称平均海面)。解决此类问题的传统方法是求解第一类Fredholm积分方程，即常用的逆Poisson积分方法。因求逆过程具有很大的不确定性，当观测量存在噪声干扰时，解算结果往往会出现较大的偏差，要想获得比较稳定的解算结果，必须采用一定的正则化处理方法[23]。为了规避扰动位向下延拓的不适定性问题，本文借鉴文献[12—13]的研究思路，提出直接求解广义带限Dirichlet边值问题，即已知飞行高度面上的Tb(r,θ,λ)=f(r,θ,λ)，求海平面(近似为球面)上的Tb(R,θ,λ)，具体表述为

(10)

由于上述边值问题的观测边界面为飞行高度面，而需要确定的扰动位解域要求涵盖海平面及其外部的所有空间，这就意味着问题解域的一部分位于观测边界面的内部。因此，从理论上讲，由式(10)定义的边值问题解也是非稳定的。带限观测量的特性可以改变边值问题解的性质，即具有带限频谱特性的观测量可以将不适定问题转变为适定问题[34-35]。其原理是，首先将上述问题表述为具有双边界面的伪边值问题[12,35]，然后对双边值面做近似处理，进而将其转换为传统的单边值面边值问题，由此可依据经典的Dirichlet边值理论，得到由式(10)定义的广义带限Dirichlet边值问题解[12-13]，即

(11)

式中，r=R+H，Yb(R,ψ,r)为扰动位带限积分核，其计算公式为

(12)

由式(12)得知，当飞行高度H和观测量带宽参数b被控制在一定的量值之内时，由式(11)可获得稳定可靠的广义带限边值问题解，这正是带限观测量能够改变边值问题解性质的缘由所在。此外，对式(11)进行实际计算时，考虑到观测数据覆盖范围的有限性，同样需要将全球积分划分为近区和远区两个部分，近区积分由实测数据计算，远区积分则由超高阶全球重力位模型计算。此时，式(11)将改化为

Yb(R,ψj,r)Δσj

(13)

式中，远区效应积分核函数Qn(H,ψ0)的计算公式为

(14)

式中，各符号意义同前。由式(13)求得海平面上的扰动位Tb(R,θ,λ)以后，即可利用著名的Bruns公式将海平面上的扰动位转化为大地水准面高度(这里不再列出Bruns公式)，也就完成了基于带限航空矢量重力测量水平分量确定大地水准面的全流程。

如前文所述，为了消除航空重力测量数据中的高频噪声影响，提高测量成果的可靠性，实践中一般都采用低通滤波器对包含噪声的重力观测数据进行滤波处理。因此，航空重力测量成果的实际空间分辨率ρ(对应半波长λ/2)主要取决于所选用低通滤波器的截止频率f(其倒数称为滤波周期T)和测量载体飞行速度v的大小，三者的关系为[7]

ρ=v/f/2=v·T/2

(15)

由式(15)可知，航空重力测量数据分辨率与飞行速度v成正比，与滤波器截止频率f成反比。由地球重力场理论得知，重力观测量的空间分辨率ρ与其相对应的球谐函数频谱展开最高阶数L存在如下关系[1]

(16)

式中，ρ的单位为角分(′)。由式(15)确定航空重力测量数据分辨率ρ以后，可依据式(16)计算该观测量所对应的球谐函数频谱展开最高阶数L，并进一步确定与其相对应的带宽b。由此得知，数据分辨率ρ与最高阶数L和带宽b存在对应关系，只要明确了前者，后两者就可以精准确定。例如，如果已知航空重力测量数据分辨率为ρ=2′，那么由式(16)可求得L=5400；当参考场模型GGM的最高阶数取为360时，即取l-1=360时，可求得带宽b=L-l=5400-361=5039。

航空矢量重力测量除了可以获取扰动重力两个水平分量外，还能获得更为重要的扰动重力垂向分量观测数据。显然，依据垂向分量同样可以通过带限模型直接或分步确定大地水准面，本文的扰动重力垂向分量采用文献[12—13]中的航空标量重力测量输出量。联合使用水平分量和垂向分量确定的大地水准面高度计算结果，必然会有效提高大地水准面的最终计算精度，频谱组合方法是最常用的多源重力信息融合处理手段之一[36]，关于这方面内容的拓展研究，笔者拟另文讨论。

2 数值计算验证

本文为了验证上述两步算法的可靠性和有效性，利用当前国际上应用广泛的重力位模型EGM2008设计了基于带限航空矢量重力测量水平分量确定大地水准面的数值仿真试验。EGM2008模型是由美国国家地理情报局(NGA)联合多家科研机构研制发布的全球超高阶地球重力场模型，由卫星重力测量、卫星测高、地面和海面重力观测等多种资料联合解算得到，模型最高完整阶次达到2160[37]。由EGM2008模型计算得到的重力异常在我国大陆的总体符合度为10.5 mGal[38]。为了对比分析，本文利用上述的逆Poisson积分方法[28]，将第1步获得的飞行高度面上的带限扰动位向下延拓到海平面，并进一步计算相对应的大地水准面，本文称之为两步逆积分法。

2.1 仿真数据准备

2.1.1 带限航空矢量重力水平分量仿真观测值计算

(17)

式中，各符号意义同前。

本文的数值试验计算范围取：5°×5°(纬度：36°N～41°N；经度:108°W～113°W)；飞行高度分别取2、3、4、5和6 km；仿真观测数据的计算格网取2′×2′。不同高度面的仿真观测量计算统计结果见表1，图1和图2分别给出了4 km飞行高度面上的两个带限水平分量等值线。

表1 带限航空矢量重力水平分量仿真观测值统计结果

为了分析研究航空矢量重力测量观测误差对大地水准面计算结果的影响，在仿真观测数据中分别加入1.5 mGal和3 mGal的随机噪声，形成两组新的模拟观测量，然后按照前面相同的计算方案和流程，完成大地水准面解算。本文试验涉及的数值计算积分半径统一取为ψ0=1°，为了减小积分边缘效应对评估结果的影响，后面开展的数值比对检核均不包含计算区域边缘1°带宽内的计算结果。

图1 4 km高度面带限南北向分量分布Fig.1 Band-limited north-south component on 4 km altitude surface

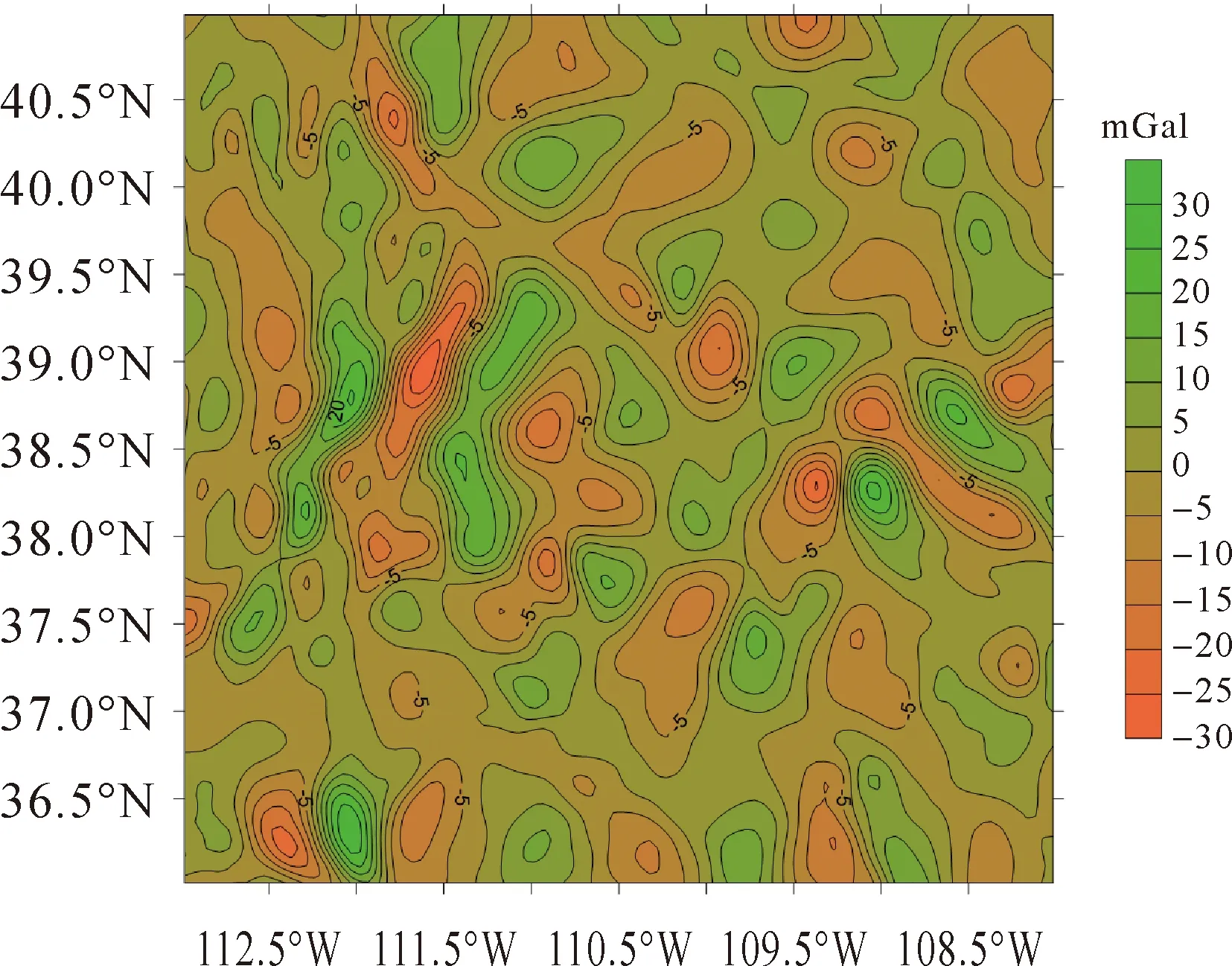
图2 4 km高度面带限东西向分量分布Fig.2 Band-limited east-west component on 4 km altitude surface

2.1.2 空中带限扰动位和海平面带限大地水准面基准值计算

在上文所述的两步积分法和两步逆积分法中，第一步都是基于带限航空矢量重力测量两个水平分量计算飞行高度面上的带限扰动重力位Tb(r,θ,λ)，为了检验该步骤计算结果的有效性，利用EGM2008位模型计算对应前面5个高度面上的带限扰动位作为比对基准值。计算公式[1]为

(18)

为了进一步检核由飞行高度面上的带限扰动位确定大地水准面的最终计算精度，利用EGM2008模型计算海平面上的带限大地水准面作为比对基准值。计算公式[1]为

(19)

式中，γ为海平面计算点处的地球正常重力。空中带限重力扰动位和带限大地水准面基准值的计算结果见表2，图3和图4分别给出了4 km高度面带限扰动位和海平面带限大地水准面的等值线。

图3 4 km高度面上的带限重力扰动位Fig.3 Band-limited disturbing gravity potential on 4 km altitude surface

图4 海平面上的带限大地水准面Fig.4 Band-limited geoid on 0 km altitude surface

2.2 数值计算结果分析

2.2.1 飞行高度面带限扰动位计算与比较

以上文事先获取的对应于5个飞行高度面的航空矢量重力测量两个水平分量的仿真观测数据(包括无误差和有误差干扰共3组数据)作为数值试验输入信息，首先依据式(6)—式(9)，分别计算相应高度面上的带限扰动位。将计算结果与基于EGM2008重力位模型计算得到的空中带限扰动位基准值进行比较，两者互差的统计结果见表3。

表2 空中带限扰动位和带限大地水准面基准值统计结果

表3 空中带限扰动位与基准值比较统计

由表3结果可以看出，空中带限扰动位计算值与仿真基准值的整体吻合情况良好，没有明显的系统性偏差，说明由广义带限水平边值问题解确定的空中带限扰动位是可靠有效的。一方面，解算结果精度随计算高度的增大只是略有提升，表明当观测量与待求量处于同一边界面时，带限扰动位计算精度几乎与飞行高度无关。这个结果也完全符合理论上的预期，因为随着飞行高度的增大，带限扰动位场高频成分会逐步减弱，其相对变化趋于平缓，带限扰动位逼近计算精度自然会得到细微的改善。另一方面，空中带限扰动位计算精度随着观测误差量级的增大而略有下降，但降低幅度并不明显，以4 km飞行高度面为例，当观测误差分别为0、1.5和3 mGal时，计算结果与基准值互差的均方根值依次为0.090、0.092和0.109 m2/s2，表明广义带限水平边值问题解具有良好的低通滤波特性，能有效抑制观测高频噪声的影响。无误差影响(即观测误差为0 mGal)条件下，带限扰动位计算结果仍然存在一定大小的偏差，是由式(2)转换为式(6)引入的数值积分离散化误差所致。这个结果也从另一侧面说明，要想进一步提高带限扰动位的解算精度，必须尽可能提高观测数据的分辨率，减小输入网格数据的间距。

2.2.2 空中带限扰动位向下延拓计算与比较

以上述计算步骤获得的对应于5个飞行高度面的带限扰动位作为输入量，分别依据式(13)和传统的逆Poisson积分模型，将空中带限扰动位向下延拓到海平面，并利用Bruns公式将延拓结果直接转换为带限大地水准面。将两组计算结果分别与基于EGM2008重力位模型计算得到的带限大地水准面基准值进行比较，两者之间的互差统计结果分列于表4和表5。

表4 本文方法计算得到的带限大地水准面与基准值比较统计结果

由表4和表5的统计结果可以看出，采用本文推导的式(13)直接将带限扰动位向下延拓到海平面，进而确定相对应的带限大地水准面，其计算效果明显好于使用传统逆Poisson积分模型的两步逆积分法，即使在有数据观测误差影响的条件下，前者的计算精度也能达到2～3 cm，而后者只在2 km飞行高度面上获得5 cm的计算精度，在其他高度面上，其计算误差均超过10 cm。对比表4、表5可进一步看出，飞行高度和数据观测误差的增大只对本文方法的计算精度产生微小影响，当观测误差为3 mGal，飞行高度从2 km增大到6 km时，本文方法的计算误差仅从1.80 cm略微增大至2.95 cm，而此时传统方法的计算误差则从5.47 cm大幅增大至30.82 cm。上述结果说明，本文提出的带限计算模型具有良好的数值稳定性和有效性，逆Poisson积分方法的计算精度则明显受到延拓高度的制约，其数值解的可靠性随计算高度的增大而迅速降低，即使没有观测噪声的干扰，由第一步骤计算过程引入的积分离散化误差就足以使逆Poisson积分数值解失效，如果不采取适当的正则化处理措施[28]，很难取得具有实际意义的计算结果。

表5 逆Poisson积分模型计算得到的带限大地水准面与基准值比较统计结果

3 结 论

精化大地水准面是航空矢量重力测量数据的主要应用方向之一。但依据航空重力测量数据确定大地水准面本质上都属于位场向下延拓的理论范畴，因此不可避免地会面临模型解算过程的不适定性问题。为了破解此难题，本文以物理大地测量边值理论为基础，提出了基于广义带限水平边值问题解和带限Dirichlet边值问题解确定大地水准面的两步积分法，较好地解决了模型解算的不稳定性问题。本文设计了所提方法与传统方法的数值计算对比试验，同时模拟仿真了两个不同量值的观测噪声影响试验，对比试验结果表明，带限计算模型在提高数值解算稳定性和抑制高频干扰噪声两个方面都具有明显的优势，在正常的航空重力测量飞行高度和噪声影响条件下，利用带限积分模型计算带限大地水准面，可取得优于3 cm的符合精度。