基于矩阵分解的可分离非线性最小二乘问题求解方法及其应用
王路遥,刘国林,王凤云,王 珂,韩 宇
山东科技大学测绘与空间信息学院,山东 青岛 266590
最小二乘估计在线性与非线性模型的参数估计理论与实际应用中都占有非常重要的地位[1],而在数据处理中大多数实际问题都涉及非线性函数模型[2]。非线性最小二乘问题是最优化理论的重要分支,也可视为无约束条件下的二次规划问题。若要在非线性数据处理中广泛使用非线性模型参数估计理论,必须进行大量深入细致的工作[3]。文献[4]推导了不等式约束整体最小二乘(inequality constrained WTLS,ICWTLS)最优解的一阶必要条件和二阶充分条件,采用有效集(active set,AS)法和序列二次规划(sequential quadratic programming,SQP)法求ICWTLS解。序列二次规划法和有效集法等算法常常被应用于求解等式或不等式约束,以及混合约束的非线性规划问题。而针对可分离非线性最小二乘问题,Golub和Pereyra提出变量投影算法,此后众多学者对变量分离后再进行解算的方法进行了深入研究。在可分离问题中,应用变量投影算法并结合Gauss-Newton方法对模型参数进行求解,函数的计算效率会有一定程度的提高[5]。文献[6]证明了变量投影和联合优化是求解可分离非线性最小二乘问题的两种截然不同的方法,其最重要的区别在于前者的不平衡信赖域假设。文献[7]通过蒙特卡洛模拟试验验证了Ruano提出的简化雅可比矩阵JR=-DFF-y不适用于变量投影算法,这可能使算法难以收敛。此外,基于矩阵的梯形分解[8]、约束方程的广义LU(lower-upper,LU)分解[9]和奇异值分解[10]等分解方法,多种变量投影的改进算法也被相继提出。
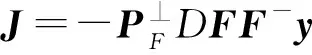
在变量投影算法与矩阵分解相结合的研究文献中,学者们在经典算法的基础上优化算法来提高求解可分离问题的效率,但其中多数只针对某种单一的矩阵分解方法与变量投影算法结合的实用性进行了探究,缺少多种方法的对比分析,且常用的满秩分解方法未与变量投影算法相结合。在空间直角坐标转换参数解算中,七参数模型具有可分离非线性模型的一般形式,而变量投影算法并未应用其中。因此,本文在经典变量投影算法的基础上进行改进,对参数分离后的非线性矩阵进行满秩分解、QR分解、奇异值分解和施密特正交化方法分解处理,导出4种变量投影公式。在数值试验部分,通过Mackey-Glass时间序列模拟试验,验证变量投影算法与基于不同矩阵分解的改进算法的优缺点,并将变量投影算法及其改进算法应用于空间直角坐标转换参数解算中,采用基于Gauss-Newton法改进的Levenberg-Marquardt(LM)法迭代计算旋转参数。通过独立坐标系和CGCS2000坐标系转换试验,验证改进的变量投影算法在此类实际问题中的可行性,并对比不同改进算法解决此类问题的优劣性,为坐标转换模型参数解算提供一种新方法。
1 可分离非线性最小二乘及其变量投影算法
可分离非线性最小二乘问题的函数模型为非线性函数的线性组合形式,一般可表示为
(1)
式中,φj(α,ti)为非线性函数部分;yi为ti对应的已知观测数据;α=(α1,α2,…,αq)T和β=(β1,β2,…,βp)T分别为待估参数。针对可分离非线性最小二乘问题,文献[21]提出了变量投影算法。在给定观测数据(ti,yi)的情况下,残差表达式为
(2)

(3)

β=Φ(α)+y
(4)
式中,Φ(α)+是Φ(α)的广义逆矩阵。将式(4)代入式(3),可得

(5)

(6)
2 基于矩阵分解的变量投影算法
2.1 满秩分解

Φ(α)=C×B
(7)
式中,C是一个m×r阶列满秩矩阵;B是一个r×p阶行满秩矩阵。因此
(8)
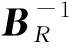
基于满秩分解的变量投影函数为
(9)
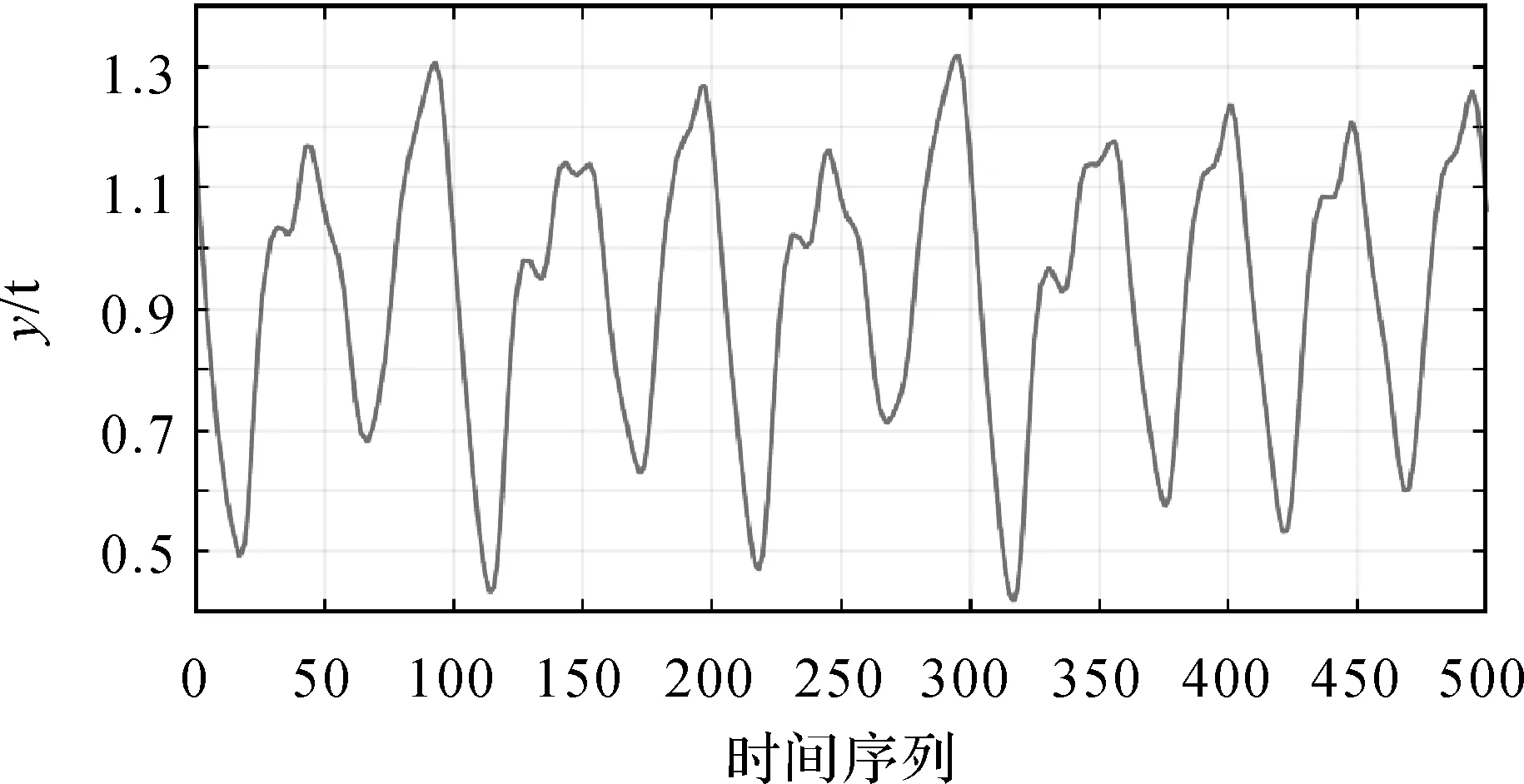
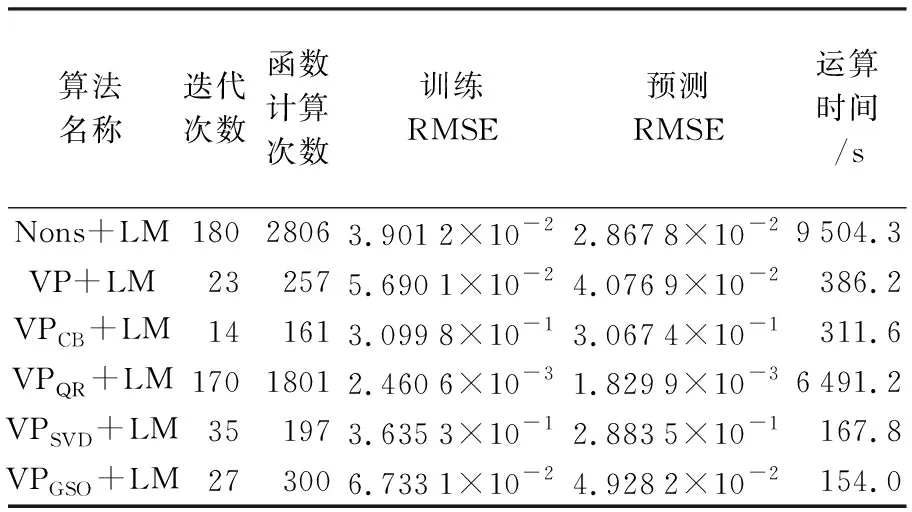
满秩分解的优势解决了矩阵秩亏问题。当m×p阶矩阵Φ(α),即r(Φ(α)) QR分解是将矩阵分解成一个正交矩阵Q与一个上三角矩阵R。将变量投影中的m×p阶矩阵Φ(α)通过QR分解方法分解为 (10) 式中,Q是一个m×m阶正交矩阵,具有Q-1=QT的性质;R为m×p阶矩阵,R1为p×p阶上三角矩阵。 (11) (12) QR分解产生了一个m×m阶正交矩阵Q,其逆矩阵与转置矩阵相同。计算机对矩阵求转置的速度比求逆的速度更快,因此能够提高运算效率。 在变量投影算法中,将m×p阶矩阵Φ(α)通过奇异值分解方法分解为 (13) 式中,U是m×m阶正交矩阵;S是m×p阶矩阵,S1为r×r阶对角矩阵(r是矩阵Φ(α)的秩),对角元素为Φ(α)的奇异值;V是p×p阶正交矩阵。 (14) (15) 奇异值分解产生了一个m×m阶正交矩阵U,具有U-1=UT的性质,同样可以加快运算速度,提高运算效率。 将变量投影函数中的Φ(α)分解为 (16) (17) (18) 则 (19) 因此 (20) 式中,G1和G2分别是m×r和m×(p-r)阶矩阵,因此变量投影函数可写为 (21) 在许多实际问题中,观测值个数要远大于求解的线性参数的个数。式(19)中m×r的矩阵G1要小于式(16)中正交化之前的矩阵Φ(α),且m×p的正交矩阵G要小于式(11)中的Q和式(14)中的U。如此,便可以在计算机存储和调用矩阵进行运算的过程中减少计算机内部存储空间,减少运算量和运算时间。 在上述改进算法中,满秩分解主要针对矩阵秩亏情况而提出,将其表示为两个矩阵相乘的形式,其他3种分解方法在分解形式上具有相似性,都可产生正交矩阵。正交矩阵的逆矩阵与其转置矩阵相同这一性质避免了计算机对大型矩阵求广义逆矩阵的过程,且对具有一定病态程度的方程组,数值解算稳定性相对较好。相比参数不分离算法和经典变量投影法,4种改进算法都可在一定程度上减小计算量,提高计算效率。 将原非线性最小二乘问题的目标函数通过矩阵分解,分别得到4种仅与非线性参数有关的目标函数ssrCB(α)、ssrQR(α)、ssrSVD(α)、ssrGSO(α),进而采用LM算法进行非线性参数估计。LM算法是在Gauss-Newton法基础上引入单位阵和阻尼因子得到,其迭代式为 αk+1=αk-(JTJ+uI)-1JTV (22) 利用LM迭代求解非线性参数的关键是如何得到迭代式中的J和V。基于变量投影算法得到参数分离后的残差向量为V=y-Φ(α)Φ(α)+y,对残差向量求关于非线性参数α的一阶偏导,得到雅可比矩阵J。假设在第k次迭代过程中,非线性参数值为αk,那么雅可比矩阵J和非线性矩阵Φ均为数值型矩阵,进而分别采用满秩分解、QR分解、奇异值分解和施密特正交分解的方法对数值型矩阵Φ进行分解。基于矩阵分解方法对非线性参数求解的步骤总结如下。 (1) 对残差向量求关于非线性参数的一阶偏导,得到雅可比矩阵J; (2) 给定迭代初值α0,设置收敛准则—迭代终止阈值ε和最大迭代次数kmax; (4) 若hLM使得ssr(αk+1) ssr(αk); (5) 若ssr(αk+1)-ssr(αk)<ε或k>kmax,则终止迭代,否则,执行步骤(3)—步骤(4)。 为了验证基于矩阵分解的变量投影算法在可分离非线性最小二乘问题求解的有效性及在测绘领域中的应用,分别采用Mackey-Glass时间序列模拟试验和独立坐标系与CGCS2000坐标系之间参数求解试验,对参数不分离方法(Nons)、经典变量投影法(VP)、基于满秩分解的变量投影法(VPCB)、基于QR分解的变量投影法(VPQR)、基于奇异值分解的变量投影法(VPSVD)和基于施密特正交化的变量投影法(VPGSO)进行了对比分析,试验环境为Matlab R2016a,1.80 GHz PC,Windows7系统。 试验利用指数模型拟合混沌型Mackey-Glass时间序列,此模型在非线性时间序列预测中具有优良的性能,且已从理论上被证明可以任意精度逼近任何函数[24]。设函数模型为 (23) (24) 式中,a=0.2,b=0.1,c=10,d=17。设初值条件y(0)=1.2,时间间隔为0.1,采用龙格库塔方法求解微分方程并生成500组数据,如图1所示。按照以下方式从生成的数据中提取100组数据:[y(t-24),y(t-18),y(t-12),y(t-6),y(t)](t=[24,123])。利用这100组数据,采用Nons+LM、VP+LM、VPCB+LM、VPQR+LM、VPSVD+LM和VPGSO+LM这6种方法估计模型中的参数,并用区间[124,200]和[400,500]内的数据进行预测。 图1 混沌型Mackey-Glass时间序列Fig.1 Chaotic Mackey-Glass time series 图2 曲线拟合Fig.2 Curve fitting 表1列出了所有方法对应的迭代次数、函数计算次数、均方根误差及运算时间。图3给出了迭代计算时,参数分离的5种算法对应的非线性参数的收敛过程。 表1 迭代次数、函数计算次数、均方根误差(RMSE)、运算时间对比 对比表1中的数据可知,模型在短期预测中所得均方根误差比训练时要小,这与文献[24]的试验结果一致,说明模型能够从训练数据中获取较好的预测能力。在解算结果精确度方面,所有方法都具有足够小的均方根误差,其结果都有较高的可信度,其中VPQR+LM算法对应的训练和预测的均方根误差数值最小,说明此种方法在拟合数据和预测趋势的过程中,其结果最为精准,但其计算效率不占据优势;Nons+LM方法迭代计算次数最多,所需时间最长,而经过分离参数的变量投影算法在这两方面有了较大幅度的减少,本文提出的VPCB+LM具有最少的迭代次数;在迭代次数与函数计算次数水平相近的情况下,VPSVD+LM和VPGSO+LM方法在运算时间上有较为显著的优势。文献[25]分别利用200、400、600组模拟试验数据,在解算结果精度相近的条件下对比验证了基于施密特正交化的变量投影法的运算效率[25],与本文所得结论相同。给定相同的迭代初值,参数分离的5种方法对应的非线性参数迭代过程如图3所示。 图3 非线性参数迭代过程Fig.3 Iteration process of nonlinear parameters 由图3可知,在给定相同初值的条件下,所有方法都有明显的收敛趋势,且VP+LM、VPCB+LM和VPGSO+LM的收敛速度较快。在区间[400,500]内进行了多步预测试验,从Mackey-Glass时间序列中的第400个点开始,每10个点一组,利用5种分离参数算法求得的模型对时间序列进一步预测至第500个点,绘制出该区间内曲线拟合效果图,并求得每一组的均方根误差RMSE,进而绘制成折线图,如图4所示。 由图4可知,VPCB+LM和VPSVD+LM算法随着预测次数的增加,其均方根误差越来越大且变化速率较快,表明其预测精度越来越低,预测能力较弱,而其他算法对应折线相对平缓,预测能力更加稳定,其结果具有较高的精度,其中VPQR+LM算法最稳定,预测效果最佳。 图4 预测曲线拟合图及分组多步预测的RMSEFig.4 Curve fitting of prediction and RMSE of multi-step prediction 在测量学科的空间直角坐标转换中,两个不同的空间直角坐标系进行转换需要用7个参数来描述,其中包括3个坐标轴的平移参数、3个旋转参数和1个坐标轴缩放参数,如果已知两空间直角坐标系下的3个及以上的公共点坐标值,那么这7个参数可以唯一确定。下面对七参数模型进行介绍。如图5所示,对于两个不同的空间直角坐标系O1X1Y1Z1和O2X2Y2Z2,它们的原点不一致,对应的坐标轴相互不平行。两个坐标系之间存在平移参数(ΔX,ΔY,ΔZ)、旋转参数(α,β,γ)和缩放参数s。 图5 坐标转换Fig.5 Coordinate transformation 在进行坐标转换时,常用的七参数模型的一般形式为 (25) 式中,(X1,Y1,Z1)为转换前的坐标值;(X2,Y2,Z2)为转换后的坐标值。式(25)可视为非线性函数的线性组合,用矩阵表示为 (26) 式中,Φ中包含的旋转角(α,β,γ)为非线性参数,其与系数矩阵呈现复杂的非线性关系[26];β中包含的平移值(ΔX,ΔY,ΔZ)和缩放参数s为线性参数。利用变量投影公式可写为 (27) 本节试验所用坐标数据为工程实测数据。为实际工程应用的便利,在测量过程中建立了适用于该工程项目的独立坐标系。下面利用独立坐标系和CGCS2000坐标系之间的转换模型参数求解试验对改进的变量投影算法进行验证。 3.2.1 试验数据与结果 在空间直角坐标转换中有多种坐标转换模型及参数解算方法,这些模型均经过线性化处理[27]。本试验采用改进的变量投影算法结合LM算法对转换模型进行求解。试验采用独立空间直角坐标系和CGCS2000坐标系下的9组公共点进行试验。试验中,独立坐标系下点坐标值的精度足够高。试验所用数据的点位分布集中在一个范围较小的局部地区。局部地区应用七参数法求得的转换参数,尤其是平移参数精度是不高的,公共点坐标很小的变化会引起参数较大的变化。因此为了保证参数解算的准确性,也为了方便验证各种算法的计算效率,数值试验按照局部地区的坐标转换进行试验。选取一组点作为原点,并分别求出各点对原点的坐标差值。设原点坐标在两空间直角坐标系下的坐标值分别为(X10,Y10,Z10)、(X20,Y20,Z20),对于原点由七参数公式可得 (28) 七参数公式与式(28)作差可得 (29) 式中含有线性参数s和非线性参数(α,β,γ)。9组公共点坐标值见表2。 表2 独立空间直角坐标系和CGCS2000坐标系下9组公共点坐标值 表3 参数解算结果的对比 由表3的结果可以看出,每种方法得到的参数值几乎相等;当计算每次迭代的残差平方和时,原始模型的残差实际上包含两种参数类型的误差,这也是在收敛分析时图6(a)中Nons+LM方法在最开始时残差平方和较大的原因。参数不分离算法的参数估计值与最优值的残差平方和最小,其他方法也都具有较小的残差,得到的结果都是足够精确的。 3.2.2 计算过程分析 除了比较数值解算结果外,试验过程中还比较了每种方法的迭代次数、函数计数次数、残差平方和及运算时间,结果见表4。 由表4可知,每种方法的迭代次数均相等,而经过参数分离的算法对应的函数计算次数均小于Nons+LM算法。Nons+LM对应的残差稍大而参数分离的方法相对较小,这表明相比于不分离而直接进行迭代的方法,变量投影算法在估计坐标转换参数时,能够减小观测值与转换模型之间的残差,使得参数计算结果更加可靠。由计算时间可以看出,参数分离的方法对应的时间相比分离前都有所减少,在解算结果精度相同的条件下,改进算法的计算速度有不同程度的提升,其中VPGSO+LM最为显著。试验利用了9组公共点求解转换参数,展开式对应形成了含有27个方程的方程组,经变量投影分离参数后,非线性函数构成27×3阶矩阵,当VPGSO+LM对目标函数进行分解时,施密特正交化中计算的矩阵G为27×3阶矩阵,比用其他方法得到的矩阵(如QR分解得到矩阵Q为27×27阶矩阵)更加简单一些,因此在计算机存储或调用此矩阵并代入函数进行计算时,时间会有所减少。在迭代次数相同、函数计算次数和残差平方和相近的情况下,VPGSO+LM方法相比于Nons+LM方法降低了估计参数维度,相比于其他改进的变量投影法又减少了计算时间。 表4 迭代次数、函数计算次数、残差平方和及运算时间的对比 3.2.3 收敛过程的对比分析 本节以试验中的旋转角α为例,分析了6种算法在迭代过程中的收敛性。由于所有方法都是基于LM算法进行计算的,因此参数分离的算法在迭代步长、方向和循环过程是基本一致的。在加入参数不分离算法进行对比时,只在图中显示了Nons+LM和VPGSO+LM对应的计算过程。Nons+LM算法的迭代过程中也包含线性参数,其迭代方向和迭代步长与参数分离的算法在数值上存在差异。参数的具体迭代过程及残差平方和的变化如图6所示。 图6 非线性参数的迭代过程及残差平方和变化过程Fig.6 Iteration process of nonlinear parameters and variation process of residual sum of squares 由图6可以看出,Nons+LM方法在初次计算时的残差要远大于VPGSO+LM,这是由于在迭代过程中线性与非线性参数统一进行计算所导致的。在参数α的迭代过程中,VPGSO+LM方法在第2次迭代过程中存在振荡,第3次迭代接近最优值,而Nons+LM方法相对稳定一些;图6(c)显示了分离变量后的5种方法迭代过程,其过程比较一致,都是在第2次迭代出现震荡之后开始接近最优值,由于迭代过程差异较小,因此将第2次迭代结果放大至图6(d),可以看出VPSVD+LM算法结果较差,而VPCB+LM相比之下最稳定。在参数迭代过程中,LM迭代法计算的是所有非线性参数每次迭代后的总体变化,因此,迭代过程中某个参数的变化出现抬升或下降并不意味着算法不好。一般采用迭代法求解非线性方程组往往只是局部收敛,这使得迭代初值很难确定[28]。当随机给定不同的初值时,分别用分离参数的5种算法估计非线性转换参数,将程序独立运行30次,计算得到每次结果的均方根误差RMSE并绘制箱形图,如图7所示。由图7可知,VPSVD+LM对应的RMSE数值的中位数最小,对应的箱形图所表示的数据整体分布区域更接近横轴,由此可见,VPSVD+LM算法受初值影响较小,程序运行得更加稳定一些。 图7 不同算法对应均方根误差分布状况Fig.7 Distribution of RMSE corresponding to different algorithms 本文结合混沌型Mackey-Glass时间序列模拟试验,全面地对比分析了变量投影法及其基于矩阵分解的4种改进算法的优缺点。参数不分离方法在解算模型时,迭代计算次数较多,运算时间最长,而分离变量的VP算法在保证解算结果精度的前提下,可有效削弱这一弊端;当非线性矩阵存在一定程度的病态时,对矩阵进行分解可使得算法迭代过程稳定,以保障解算的有效性;改进的算法在迭代次数、解算精度、计算效率、预测能力及稳定性等方面也有不同程度的提升。在解算可分离问题的模型参数时,若参数最优值所在区间不可知,在不追求运算效率的情况下可选用VPQR+LM,若考虑运算效率而对精度要求较低,则建议使用VPCB+LM或VPSVD+LM,若两者都须顾及则可选用VPGSO+LM;若已知其最优值所在区间,可使用VPGSO+LM算法并设置迭代初值在最优值附近,以追求参数求解的计算效率;在解得模型参数后,可使用VPQR+LM进行数据预测。 在基于矩阵分解推导变量投影公式的过程中发现,当非线性矩阵Φ(α)秩亏时满秩分解具有较大优势,其余3种矩阵分解法最终都将非线性矩阵及其逆阵的乘积PΦ(α)导出为正交矩阵与含有单位阵矩阵相乘,其形式具有统一性,而正交矩阵的逆矩阵与其转置相同这一性质使得算法在求解模型参数时简化了计算过程,节约了运算时间。 本文将变量投影法及改进算法应用于空间直角坐标转换模型参数求解中,并对算法的实用性进行了探究。经试验发现,该算法及改进算法适用于解算坐标转换模型参数,且4种改进算法在解决此类问题的运算效率方面有所提升。在转换参数求解中应用改进的变量投影算法,可在保证求解结果精度的同时降低待估计参数的维数,简化非线性函数矩阵大小,提高计算机的变量存储、调用和计算的速度,使运算时间最小化,为坐标转换模型参数的求解提供了新的方法,对丰富可分离非线性最小二乘理论在测绘领域中的应用具有实际意义。2.2 QR分解


2.3 奇异值分解


2.4 施密特正交分解
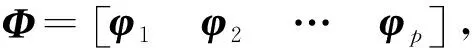

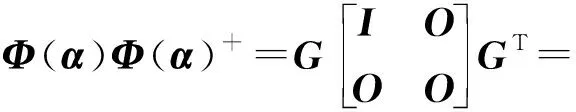

3 数值试验
3.1 Mackey-Glass时间序列




3.2 空间直角坐标转换模型参数求解试验

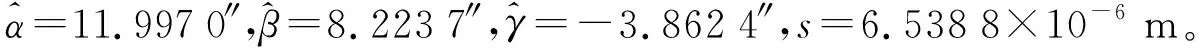





4 结 论

