顾及ISB/IFB的多GNSS RTK/INS紧组合导航方法
郝雨时,孙剑伟,隋 心,徐爱功,施 闯,4
1. 北京航空航天大学电子信息工程学院,北京 100083; 2. 中国电子科技集团公司第十五研究所,北京 100083; 3. 辽宁工程技术大学测绘与地理科学学院,辽宁 阜新 123000; 4. 卫星导航与移动通信融合技术工信部重点实验室,北京 100083
GNSS/INS组合导航技术广泛应用于室外复杂环境下的位置、速度及姿态测量[1]。已有研究成果表明,采用基于相位观测值的多GNSS RTK/INS紧组合方式,结合模糊度快速固定策略可实现厘米级别定位精度[2-4]。因不同卫星系统信号存在差异,模糊度固定多采用GNSS系统内部固定的方式。虽然采用多GNSS组合在一定程度上可以增加可视卫星数,但是复杂环境下信号遮挡导致单GNSS系统内部有效卫星数量少,多GNSS/INS紧组合整周模糊度固定依然困难。
为进一步发挥复杂环境下多卫星系统的互补性,相关学者致力于研究不同卫星系统间模糊度固定方法,其本质是研究不同卫星系统间相位频间差(IFB)、系统间相位偏差(ISB)与模糊度降相关问题。ISB/IFB参数处理方式主要有赋初值后进行估计[5-8]和直接作为参数估计[9-16]2种。第1种方式依赖于初值精度,考虑接收机端ISB参数不稳定[15,17]、IFB参数易受设备因素影响[18-20]等问题,无法准确确定初值。文献[8—10]采用直接估计的方式,需进行长时间数据采集,不利于实时估计。文献[15—16]分别采用粒子滤波和粒子群优化方法,表现效果良好,而采用粒子群优化算法无须遍历搜索区间内的所有粒子,ISB/IFB估计可根据个体和群体历史最优位置来驱动粒子快速朝最优位置运动,效率较高。目前,以上方法均针对GNSS数据处理,鲜有针对卫星/惯性组合导航数据处理的应用与测试。虽然GNSS RTK/INS紧组合方式较GNSS RTK方式在复杂观测环境下更具优势,但在相对极端的复杂观测环境下,会出现长时、频繁的观测异常或信号中断,此时的GNSS观测冗余度难以保证模糊度固定的连续性,导致状态估计不确定度增大,INS状态模型精度降低,短时高精度优势难以发挥。另外,当前ISB/IFB参数估计是建立在利用EKF进行状态浮点解估计基础之上的,EKF结合故障探测与排除策略可抑制非高斯噪声对状态估计的影响,提高卫星/惯性组合导航浮点解精度[21-22],浮点解精度对顾及ISB/IFB参数的系统间模糊度固定的影响尚未得到验证。
据此,本文基于卫星系统间模糊度固定理论成果,提出顾及ISB/IFB的多GNSS RTK/INS紧组合方法,构建顾及ISB/IFB的紧组合导航观测方程,给出结合抗差滤波算法和粒子群优化算法的ISB/IFB参数估计方法,并利用试验验证顾及ISB/IFB参数对紧组合导航系统的影响及浮点解精度对紧组合导航卫星系统间模糊度固定的影响。
1 顾及ISB/IFB的多GNSS RTK/INS紧组合导航方法
卫星/惯性组合导航方程包括状态方程和观测方程。状态方程以INS漂移误差角ψ误差方程[23-24]为核心,在此基础上增广模糊度参数误差方程及ISB/IFB参数误差方程。模糊度及ISB/IFB参数建模为随机常数。ψ误差方程推导过程在诸多文献中均有详细介绍,本文不再赘述。本节内容为顾及ISB/IFB的多GNSS RTK/INS紧组合导航观测方程和ISB/IFB参数估计方法。
1.1 观测方程
短基线条件下的GNSS系统间双差观测方程为
(1)
式中,Δ∇代表双差后的参数;Δ代表单差后的参数;上标Ms和Fl中,M和F表示卫星系统,s和l表示卫星号;L表示相位观测值;P表示伪距观测值;N为整周模糊度;λ为波长;相位硬件延迟表现为一个常数项和一个与频率成正比的线性组合[25-26];ε和ξ为相位噪声和伪距噪声。
根据双差观测方程两卫星所属的卫星系统及信号调制技术,式(1)中Δ∇αFM、kMs、kFl和γ的取值与含义均不同:
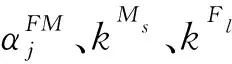


将观测方程在INS推算的地心地固坐标系下接收机天线相位中心位置进行泰勒级数展开,得到线性化后的双差观测方程为
(2)

(3)

(4)
假定lb已精确标定,对式(4)进行扰动分析,有
(5)
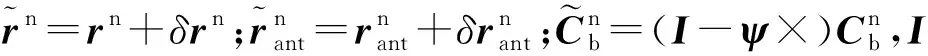
(6)
将式(6)、式(3)代入式(2),得到顾及ISB/IFB的多GNSS RTK/INS紧组合观测方程为
(7)
1.2 ISB/IFB参数估计
目前,基于PSO算法的ISB/IFB参数估计方法是建立在利用EKF估计状态浮点解的基础上进行的,因此可以认为浮点解精度会对ISB/IFB参数估计造成影响。理论上,只有在随机动态系统的结构参数和噪声分布参数精确已知的条件下,Kalman滤波可实现状态最优估计。在大部分实际应用中,随机动态系统的结构参数可精确获取,而噪声分布参数难以精确跟踪。因此,须采用某种自适应估计或抗差估计方法降低量测噪声分布参数统计偏差对浮点解精度的影响。
根据Kalman滤波量测更新过程,过程噪声参数和量测噪声参数通过卡尔曼增益决定系统状态预计及量测信息对状态估计的影响程度,若噪声参数不能准确反映状态预计及量测信息的误差水平,将引起卡尔曼增益异常,继而导致状态估计偏差。因此,自适应/抗差卡尔曼滤波主要解决的是滤波器噪声参数辨识问题[28]。对于卫星/惯性组合导航系统,系统噪声参数反应惯性器件固有误差特性,可标定且稳定性高,即便存在微小的统计偏差,也不会对状态估计精度产生严重影响。考虑复杂环境下GNSS信号中断、多路径等因素影响,量测信息中常包含未知分布特性的观测异常,若不对其进行识别,这种观测异常不仅会通过系统对状态估计造成正反馈,降低浮点解精度,还会降低INS动力学模型精度,致使滤波器系统更新精度降低,严重时可导致滤波发散或数值计算问题。因此,有必要对量测噪声参数作抗差处理。
采用IGG Ⅲ模型[27,29]对量测噪声矩阵进行调谐
(8)
式中,βii为Rk第i行i列元素的权系数;m0、m1为经验常数;γi为标准化后的新息向量中的第i个元素,表达式为
(9)

(10)

在利用以上方法估计浮点解的基础上,利用PSO算法进行ISB/IFB参数估计[20],流程如下:
(2) 以多维ISB/IFB参数作为PSO搜索目标对PSO算法参数进行初始化,包括粒子个数、群体最大迭代次数、最大和最小惯性因数、学习因子和、粒子位置变量的最大值和最小值、粒子速度变量的最大值和最小值、停止迭代条件、粒子的初始位置和速度。
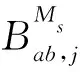
(11)

(4) 利用D将单差模糊度投影为双差模糊度,并利用LAMBDA方法进行模糊度固定。将ratio值考虑为当前粒子的适应度值。
(5) 根据适应度值更新粒子的个体历史最优位置。
(6) 根据所有粒子的个体历史最优位置更新粒子群体的历史最优位置。
(7) 根据粒子的个体历史最优位置和群体历史最优位置对粒子的位置和速度进行更新
(12)
式中
(13)
(8) 若更新后粒子位置或速度大于阈值,重新对粒子的位置和速度进行初始化。
(9) 若Gb对应的适应度值超过适应度阈值,或迭代次数达到群体最高迭代次数,将Gb作为相位偏差的最优估值。否则,重复执行步骤(3)—步骤(9),直至满足停止迭代条件。
(10) 利用ISB/IFB估值对单差模糊度参数进行改正,再投影至双差模糊度并进行模糊度固定。
2 试验分析
设计室外复杂环境多GNSS RTK/INS紧组合试验,其中多GNSS代表GPS+BDS+GLONASS+Galileo 4个卫星系统的总和。组合导航系统中,惯性器件陀螺仪零偏稳定性不超过0.1(°)/h,陀螺仪零偏重复性不超过0.1(°)/h,加速度计零偏稳定性不超过60 μg,加速度计零偏重复性不超过60 μg;另设置Leica GS15测量级GNSS信号接收机进行多GNSS数据采集。惯性导航系统采样率为200 Hz,GNSS接收机采样率为1 Hz,共采集1490 s实测数据,初始对准时间为包括343 s。试验轨迹如图1所示,总里程为9 071.141 m,试验环境包括卫星开阔观测环境,同时包括高层建筑、居民住宅等复杂观测环境。

图1 紧组合试验轨迹Fig.1 The trajectory of tightly-coupled field test
通常情况下,卫星截止高度角为10°~15°。为更好地验证弱GNSS观测环境下顾及ISB/IFB参数的系统间模糊度固定对组合导航系统的影响,试验将卫星截止高度角设为25°,该观测条件下的可视卫星数量及PDOP值分布如图2所示。试验前半时段存在少部分卫星遮挡严重的情况,PDOP值分布较为稳定。后半时段信号遮挡情况频繁,可视卫星数量变化范围相对较大,最少可视卫星数量仅为2。
设计4种试验方案(表1)。4种方案均采用GNSS单频观测值,利用单向滤波进行数据处理。方案1、方案3及方案4中涉及的m0、m1分别为2.5和8.5。对方案2、方案4的PSO算法参数进行设置:粒子个数与最大迭代次数设为10;wmin和wmax分别设为0.2和1.2;c1和c2均设为2;粒子位置变量的最大值和最小值分为设为0.1和-0.1;粒子速度变量的最大值和最小值分别为0.03和0;适应度阈值设为4.5。4种方案观载波相位测噪声参数为0.01 m,INS状态参数包括平面位置、平面速度、姿态误差角、加表零偏、陀螺零偏,其初始状态噪声参数及过程噪声参数见表2。表2中,Tm为马尔可夫相关时间,取4 h。
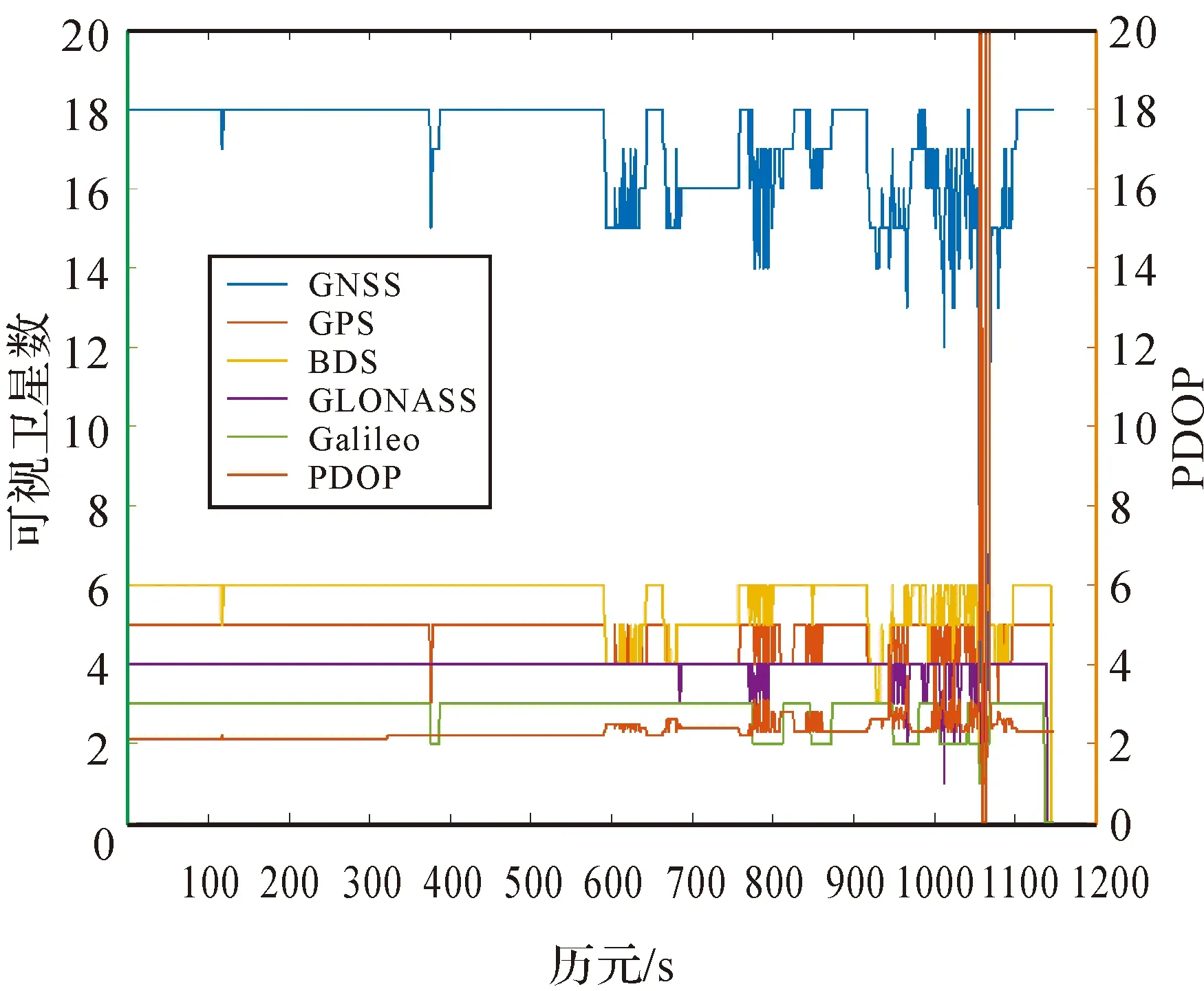
图2 可视卫星数与PDOPFig.2 Distribution of visible satellite number and PDOP

表1 试验方案

表2 噪声参数
为客观评价不同方案的精度,参考值利用国内成熟组合导航系统数据处理软件的双频多GNSS RTK/INS双向平滑数据处理结果,其精度指标见表3。

表3 参考值精度指标
对ratio值、ISB/IFB、位置、姿态偏差的时间序列进行展示,分别如图3—图6所示。其中,图3对Y轴进行了缩放,只显示小于20的ratio值结果,以清晰展示4种方案ratio值小于3的结果。结果表明,ISB/IFB估计结果整体上均在合理范围内波动,两方案无明显差异。其中,ISB-GR为GPS-GLONASS间系统偏差,ISB-GE为GPS-Galileo间系统偏差,ISB-GC为GPS-BDS间系统偏差,IFB-R为GLONASS IFB变化率。在良好卫星观测条件下,4种方案大部分时段可实现模糊度固定,定位精度可达厘米级,横滚角、俯仰角精度可达0.03°,航向角可达0.3°。在400~430历元之间,方案1出现了模糊度固定失败的情况,方案2考虑ISB/IFB参数估计,实现了模糊度固定。在520~630历元之间,4种方案频繁出现模糊度固定失败的情况,而考虑INS短时高精度特性及抗差顾及方法,位姿解算未出现较大偏差。在300~360历元之间,方案1和方案2出现模糊度固定失败,定位精度降低至0.1 m,方案3和方案4模糊度固定与位置解算均未受到影响。在1050~1147历元之间,可视卫星急剧下降且变化幅度较大,PDOP值分布不稳定,4种方案的模糊度固定成功率明显降低,方案1、方案2基本无法实现模糊度固定,位姿解算存在较大偏差,方案2姿态解算略优于方案1,但没有明显改善。在1100历元之后,可视卫星数量逐渐增加,方案1和方案2仍无法实现正常模糊度固定且位姿偏差较大。方案3、方案4模糊度固定优于其他方案,姿态解算回归正常且精度相当,方案3在1100历元后出现少量固定解,但位置解算仍存在较大偏差,方案4全部固定成功且位置解算精度改善明显。
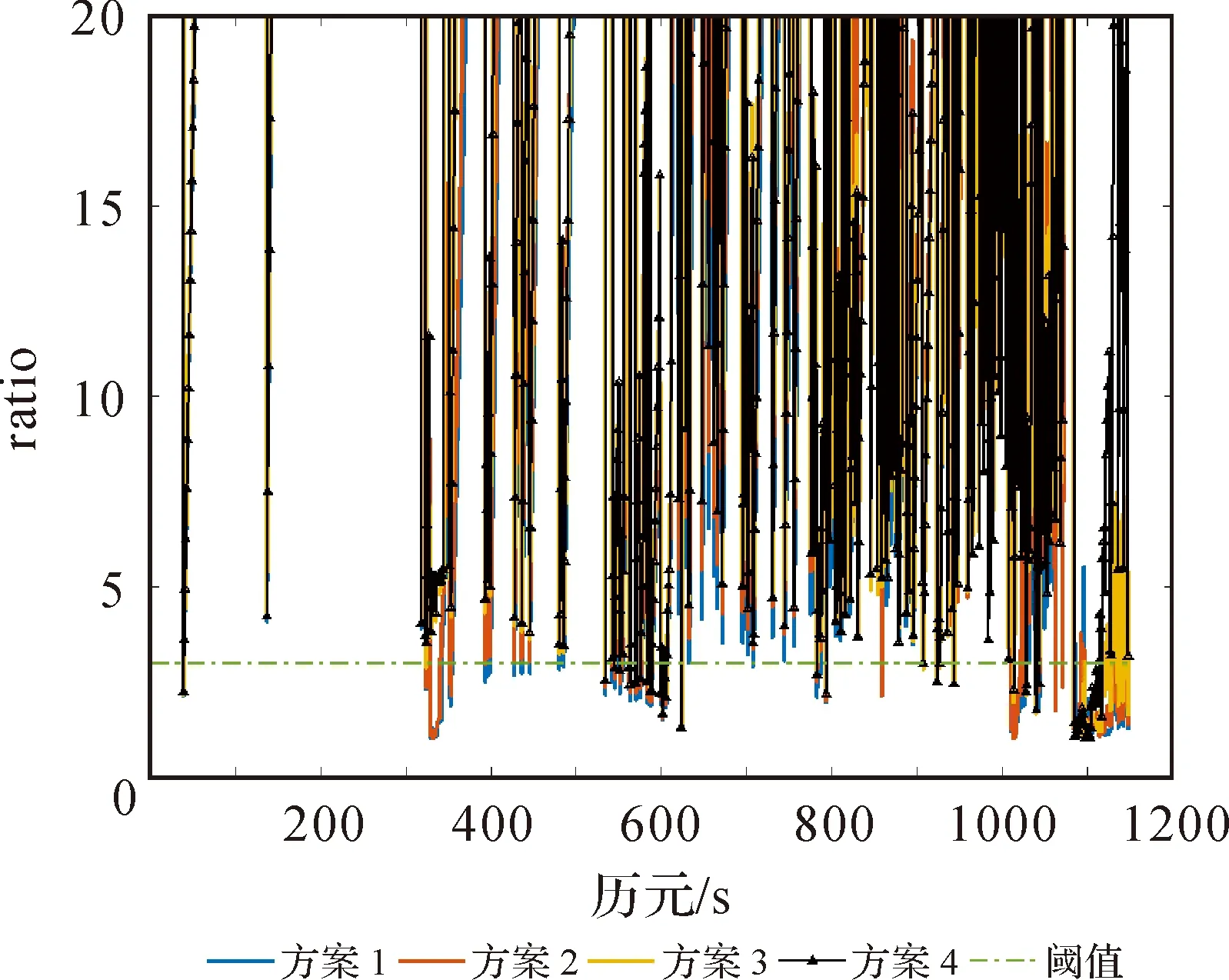
图3 不同方案ratio值分布Fig.3 Ratio distribution of different schemes

图4 不同方案ISB/IFB分布Fig.4 ISB/IFB distribution of different schemes
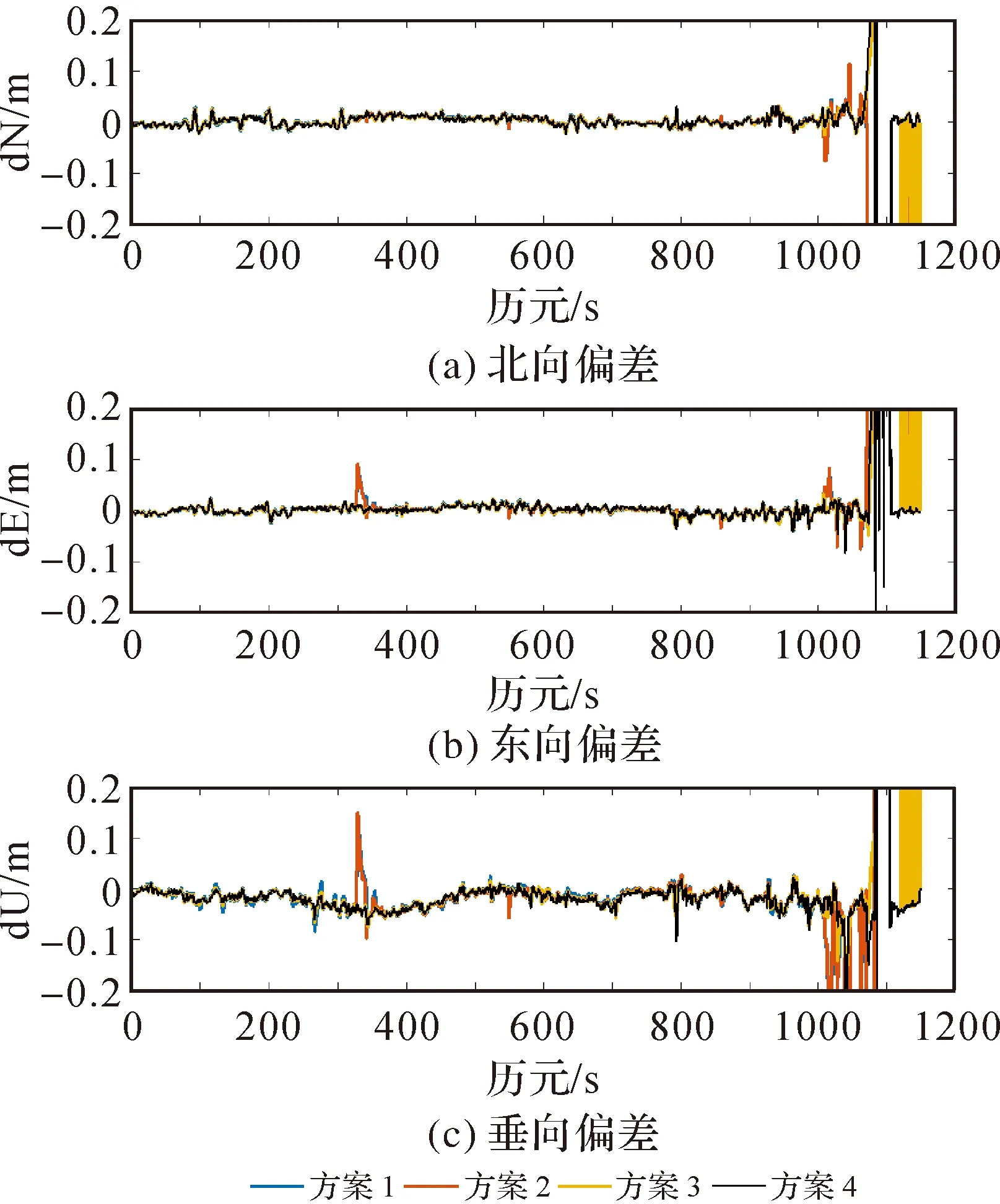
图5 不同方案位置偏差分布Fig.5 Position deviation distribution of different schemes
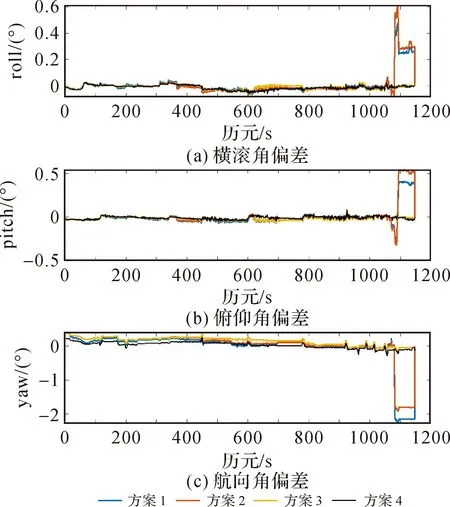
图6 不同方案姿态偏差分布Fig.6 Attitude deviation distribution of different schemes
由图2可知,600历元后可视卫星数量及DOP出现波动,后期频繁出现卫星遮挡的情况。为体现提出方法在复杂环境下的优势,下文对复杂环境下(600历元以后)的数据处理结果进行评价。模糊度固定解、东(E)北(N)高(U)方向不同位置偏差区间、姿态角(横滚角roll、俯仰角pitch、航向角yaw)的百分比统计分别见表4—表6。统计结果表明:方案2在方案1的基础上,顾及了ISB/IFB参数估计,模糊度固定成功率、位姿精度均有所提高;方案3未顾及ISB/IFB参数估计,结合抗差估计算法,模糊度固定成功率、位姿精度较方案2提升效果明显;方案4结合抗差估计及ISB/IFB参数估计,模糊度固定成功率、位姿精度提升效果优于其他方案。

表4 模糊度固定解百分比
通过以上分析,可以认为本文提出的紧组合导航方法在复杂环境下具有一定优势。同时,得到以下结论:
(1) 在利用EKF估计状态浮点解的基础上,采用顾及ISB/IFB参数的系统间模糊度固定方式可在一定程度上提高复杂环境下多GNSS RTK/INS紧组合导航系统模糊度固定成功率,并提高位姿解算精度,但改进效果没有采用抗差估计而不顾及ISB/IFB参数的方法明显,说明多GNSS RTK/INS紧组合导航系统数据处理性能受量测噪声的影响大于受ISB/IFB的影响。
(2) 在采用抗差估计方法的基础上,顾及ISB/IFB估计可进一步改善复杂环境下模糊度固定和位姿解算,相对于EKF与顾及ISB/IFB参数估计相结合的方式,模糊度固定成功率及位姿解算精度显著提高,说明顾及ISB/IFB参数的系统间模糊度固定依赖于浮点解精度,量测异常会通过影响浮点解估计影响系统间模糊度固定的性能。
(3) 在复杂观测环境下,对于短时的观测异常或信号中断,抗差估计方法可充分发挥INS短时高精度特性,降低状态估计受观测异常的影响,提高模糊度固定成功率。然而,在频繁的观测异常、信号中断情况下,长时间模糊度固定失败会使状态估计不确定度逐渐增大,INS状态模型精度降低,组合导航系统无法发挥INS短时高精度优势。此时,顾及ISB/IFB参数估计可提高模糊度固定成功率,抑制状态估计不确定度的增大,保证INS状态模型精度与短时高精度特性,降低组合导航系统受观测异常的影响。

表5 不同位置偏差区间百分比

表6 不同姿态偏差区间百分比
3 结束语
本文在已有GNSS系统间模糊度固定理论成果的基础上,推导了顾及ISB/IFB的多GNSS RTK/INS紧组合导航模型,基于紧组合导航系统噪声参数特性分析给出了结合抗差估计方法与PSO算法的ISB/IFB参数估计方法,最后利用试验验证本文方法的可行性并得到有益结论。试验结果表明,在复杂环境下,顾及ISB/IFB参数估计可以在一定程度上提高紧组合导航系统的模糊度固定成功率及位姿解算精度,利用抗差估计方法提高状态估计浮点解精度后可进一步提高紧组合导航卫星系统间模糊度固定成功率,提高位姿解算精度。

